1.1: Solving Linear Equations in One Variable

Learning Objectives

• Verify linear solutions.
• Use the properties of equality to solve basic linear equations.
• Clear fractions from equations.
• Apply linear equations.

Prerequisite Skills

Before you get started, take this prerequisite quiz.

1. Simplify \(2-6(4-7)^2\) without using a calculator.

Click here to check your answer

\(-52\)

If you missed this problem, review here. (Note that this will open a different textbook in a new window.)

2. Simplify \(7x−1−4x+5\).

Click here to check your answer

\(3x+4\)

If you missed this problem, review here. (Note that this will open a different textbook in a new window.)

3. Evaluate \(6x−4\) when \(x=−2\).

Click here to check your answer

\(-16\)

If you missed this problem, review here. (Note that this will open a different textbook in a new window.)

4. Evaluate \(-5x^2−x+9\) when \(x=-3\).

Click here to check your answer

\(-33\)

If you missed this problem, review here. (Note that this will open a different textbook in a new window.)

Linear Equations and Their Solutions

An equation¹²⁹ is a statement indicating that two algebraic expressions are equal. A linear equation with one variable¹³⁰, \(x\), is an equation that can be written in the standard form \(ax + b = 0\) where \(a\) and \(b\) are real numbers and \(a ≠ 0\). For example

\(3 x - 12 = 0\)

A solution¹³¹ to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation \(3x − 12 = 0\) is \(x\) and the solution is \(x = 4\). To verify this, substitute the value \(4\) in for \(x\) and check that you obtain a true statement.

\(\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}\)

Alternatively, when an equation is equal to a constant, we may verify a solution by substituting the value in for the variable and showing that the result is equal to that constant. In this sense, we say that solutions “satisfy the equation.”

Example \(\PageIndex{1}\):

Is \(a=2\) a solution to \(−10a+5=−25\)?

Solution

Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, and then substitute the appropriate values. By making use of parentheses, we avoid some common errors when working the order of operations.

\(\begin{align*} - 10 a + 5 &= -25 \\ - 10 ( \color{Cerulean}{2} \color{Black}{ ) +} 5 & = -25 \\ -20 + 5 & = -25 \\ -15 &\neq 25\:\: \color{red}{✗}\end{align*}\)  

Answer:

No, \(a=2\) does not satisfy the equation and is therefore not a solution.

Finding Solutions to Linear Equations

Developing techniques for solving various algebraic equations is one of our main goals in algebra. This section reviews the basic techniques used for solving linear equations with one variable. We begin by defining equivalent equations¹³² as equations with the same solution set.

\(\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}\)

Here we can see that the three linear equations are equivalent because they share the same solution set, namely, \(\{7\}\). To obtain equivalent equations, use the following properties of equality¹³³. Given algebraic expressions \(A\) and \(B\), and real number \(c\):

Addition property of equality:	If \(A=B\), then \(A\color{Cerulean}{+c}\color{Black} = B\color{Cerulean}{+c}\)
Subtraction property of equality:	If \(A=B\), then \(A\color{Cerulean}{-c}\color{Black} = B\color{Cerulean}{-c}\)
Multiplication property of equality:	If \(A=B\), then \(\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}\)
Division property of equality:	If \(A=B\), then \(\frac{A}{\color{Cerulean}{c}}\color{Black} = \frac{B}{\color{Cerulean}{c}}, \color{Cerulean}{c}\color{Black} \neq {0}\)

Table 1.1.1

Note

Multiplying or dividing both sides of an equation by \(0\) is carefully avoided. Dividing by \(0\) is undefined and multiplying both sides by \(0\) results in the equation \(0 = 0\).

Typically linear equations are not given in standard form, and so solving them requires additional steps. When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:

• Step 1: Simplify both sides of the equation using the order of operations and combine all like terms on the same side of the equal sign.
• Step 2: Use the appropriate properties of equality to combine like terms on opposite sides of the equal sign. The goal is to obtain the variable term on one side of the equation and the constant term on the other.
  • Step 2a: Add or subtract as needed to isolate the variable.
  • Step 2b: Divide or multiply as needed to isolate the variable.
• Step 3: Check to see if the answer solves the original equation.

Examples 2-4 below already have Step 1 completed, and are known as just two-step equations.

We solve algebraic equations by isolating the variable with a coefficient of 1. If given a linear equation of the form \(ax + b = c\), then we can solve it in two steps. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking the solution in the following examples is left to the reader.

Example \(\PageIndex{2}\):

Solve: \(7x − 2 = 19\).

Solution

\(\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} & & \color{Cerulean}{Add\: 2\: to\: both\: sides.} \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } & & \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}\)

Answer:

The solution is \(3\).

Example \(\PageIndex{3}\):

Solve: \(56 = 8 + 12y\).

Solution

When no sign precedes the term, it is understood to be positive. In other words, think of this as \(56 = +8 + 12y\). Therefore, we begin by subtracting \(8\) on both sides of the equal sign.

\(\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}\)

It does not matter on which side we choose to isolate the variable because the symmetric property¹³⁴ states that \(4 = y\) is equivalent to \(y = 4\).

Answer:

The solution is \(4\).

Example \(\PageIndex{4}\):

Solve: \(\frac { 5 } { 3 } x + 2 = - 8\).

Solution

Isolate the variable term using the addition property of equality, and then multiply both sides of the equation by the reciprocal of the coefficient \(\frac{5}{3}\).

\begin{aligned} \frac { 5 } { 3 } x + 2 & = - 8 \\ \frac { 5 } { 3 } x + 2 \color{Cerulean}{- 2} & = - 8 \color{Cerulean}{- 2}\quad \color{Cerulean}{Subtract\: 2\: on\: both\: sides.} \\ \frac { 5 } { 3 } x & = - 10 \\ \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{ \cdot} \frac { 5 } { 3 } x & = \color{Cerulean}{\frac { 3 } { \cancel{5} }} \color{Black}{\cdot} ( \overset{-2}{\cancel{-10}} )\quad \color{Cerulean}{Multiply \:both \:sides\: by\: \frac{3}{5}.} \\ 1x & = 3 \cdot ( - 2 ) \\ x & = - 6 \end{aligned}

Answer:

The solution is \(−6\).

Exercise \(\PageIndex{1}\)

Solve: \(4+3x=-14\)

Answer

\(x=-6\)

We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. If this is the case, then it is best to simplify each side first before solving. Normally this involves combining same-side like terms.

Note

At this point in our study of algebra the use of the properties of equality should seem routine. Therefore, displaying these steps in this text, usually in blue, becomes optional.

Example \(\PageIndex{5}\):

Solve: \(- 4 a + 2 - a = 1\).

Solution

First combine the like terms on the left side of the equal sign.

\(\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}\)

Always use the original equation to check to see if the solution is correct.

\(\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}\)

Answer:

The solution is \(\frac{1}{5}\).

Given a linear equation in the form \(ax + b = cx + d\), we begin the solving process by combining like terms on opposite sides of the equal sign. To do this, use the addition or subtraction property of equality to place like terms on the same side so that they can be combined. In the examples that remain, the check is left to the reader.

Example \(\PageIndex{6}\):

Solve: \(−2y − 3 = 5y + 11\).

Solution

Subtract \(5y\) on both sides so that we can combine the terms involving y on the left side.

\(\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}\)

From here, solve using the techniques developed previously.

\(\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}\)

Answer:

The solution is \(−2\).

Solving will often require the application of the distributive property in order to simplify each side of the equation.

Example \(\PageIndex{7}\):

Solve: \(- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )\).

Solution

Simplify the linear expressions on either side of the equal sign first.

\(\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}\)

Answer:

The solution is \(\frac{1}{3}\).

Example \(\PageIndex{8}\):

Solve: \(5(3−a)−2(5−2a)=3\).

Solution

Begin by applying the distributive property.

\(\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}\)

Here we point out that \(−a\) is equivalent to \(−1a\); therefore, we choose to divide both sides of the equation by \(−1\).

\(\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}\)

Alternatively, we can multiply both sides of \(−a=−2\) by negative one and achieve the same result.

\(\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}\)

Answer:

The solution is \(2\).

Exercise \(\PageIndex{2}\)

Solve: \(6 - 3 ( 4 x - 1 ) = 4 x - 7\).

Answer

\(x=1\)

Video Solution: www.youtube.com/v/NAIAZrFjU-o

Clearing Fractions from Equations

The coefficients of linear equations may be any real number, even decimals and fractions. When this is the case it is possible to use the multiplication property of equality to clear the fractional coefficients and obtain integer coefficients in a single step. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD). This will clear the equation of fractions.

Example \(\PageIndex{9}\):

Solve: \(\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1\).

Solution

Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, it is the \(LCD (3, 5) = 15\).

\(\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}\)

Answer:

The solution is \(−9\).

It is important to know that this technique only works for equations. Do not try to clear fractions when simplifying expressions. As a reminder:

Expression	Equation
\(\frac { 1 } { 2 } x + \frac { 5 } { 3 }\)	\(\frac { 1 } { 2 } x + \frac { 5 } { 3 }=0\)

Table 1.1.2

We simplify expressions and solve equations. If you multiply an expression by \(6\), you will change the problem. However, if you multiply both sides of an equation by \(6\), you obtain an equivalent equation.

Incorrect	Correct
\( \frac { 1 } { 2 } x + \frac { 5 } { 3 }\) \(\begin{aligned} \neq & \color{red}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} \\ = & 3 x + 10 \quad \color{red}{✗} \end{aligned}\)	\(\begin{aligned} \frac { 1 } { 2 } x + \frac { 5 } { 3 } & = 0 \\ \color{Cerulean}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} & = \color{Cerulean}{6 \cdot}\color{Black}{ 0} \\ 3 x + 10 & = 0\quad\color{Cerulean}{✓} \end{aligned}\)

Table 1.1.3

Exercise \(\PageIndex{3}\)

Solve: \(\frac{5}{6} + \frac{1}{2}x=4x-\frac{2}{3}\).

Answer

\(x=1\)

Note than multiplying by any factor of 2, 3, and 6 will clear the equation of fractions. While the LCD is officially 6 in this problem, multiplying by 6, 12, 18, or 36 will also work.

Applications Involving Linear Equations

Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.

Key Words	Translation
Sum, increased by, more than, plus, added to, total	\(+\)
Difference, decreased by, subtracted from, less, minus	\(-\)
Product, multiplied by, of times, twice	\(\cdot\)
Quotient, divided by, ratio, per	\(÷\)
Is, total, result	\(=\)

Table 1.1.4

When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify the variable, “let x represent…” and state in words what the unknown quantity is. This step not only makes our work more readable, but also forces us to think about what we are looking for.

Example \(\PageIndex{10}\):

When \(6\) is subtracted from twice the sum of a number and \(8\) the result is \(5\). Represent this as an algebraic equation and find the number.

Solution

Let n represent the unknown number.

Figure 1.1.1

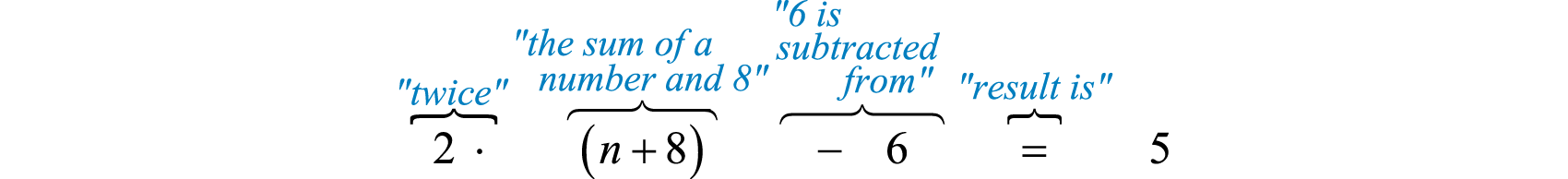
To understand why we included the parentheses in the set up, you must study the structure of the following two sentences and their translations:

“twice the sum of a number and 8”	2(n+8)
“the sum of twice a number and 8”	2n+8

Table 1.1.5

The key was to focus on the phrase “twice the sum,” this prompted us to group the sum within parentheses and then multiply by \(2\). After translating the sentence into a mathematical statement we then solve.

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}\)

Check.

\(\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}\)       

Answer:

The number is \(−\frac{5}{2}\).

General guidelines for setting up and solving word problems follow.

• Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
• Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
• Step 3: Translate and set up an algebraic equation that models the problem.
• Step 4: Solve the resulting algebraic equation.
• Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).

For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.

Footnotes

¹²⁹Statement indicating that two algebraic expressions are equal.

¹³⁰An equation that can be written in the standard form \(ax + b = 0\), where \(a\) and \(b\) are real numbers and \(a ≠ 0\).

¹³¹Any value that can replace the variable in an equation to produce a true statement.

¹³²Equations with the same solution set.

¹³³Properties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.

¹³⁴Allows you to solve for the variable on either side of the equal sign, because \(x = 5\) is equivalent to \(5 = x\).

¹³⁵Equations that are true for particular values.

¹³⁶An equation that is true for all possible values.

¹³⁷An equation that is never true and has no solution.