3.3: Linear Programming - Maximization Applications
- Page ID
- 147290
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, you will learn to:
- Recognize the typical form of a linear programming problem.
- Formulate maximization linear programming problems.
- Graph feasible regions for maximization linear programming problems.
- Determine optimal solutions for maximization linear programming problems.
Before you get started, take this prerequisite quiz.
1. Graph this system of inequalities:
\(\left\{\begin{array} {l} 2x+4y\leq 10\\3x−5y<15\end{array}\right.\)
- Click here to check your answer
-
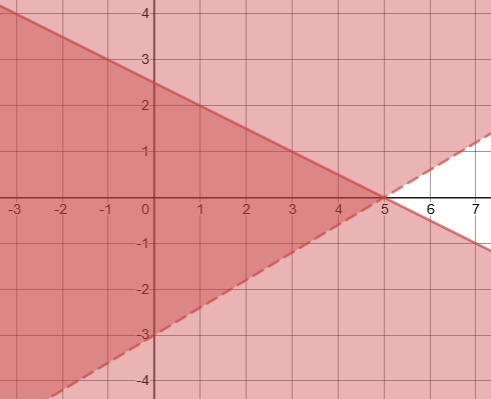
If you missed this problem, review Section 2.3. (Note that this will open in a new window.)
2. Graph this system of inequalities:
\(\left\{\begin{array} {l} y\leq 2x+1\\y\leq-3x+6\\x\geq0\\y\geq0\end{array}\right.\)
- Click here to check your answer
-
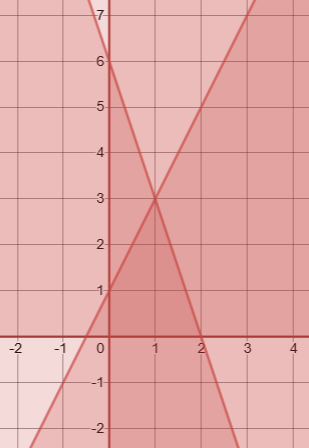
(The solution is in the center region.)
If you missed this problem, review Section 2.3. (Note that this will open in a new window.)
Application problems in business, economics, and social and life sciences often ask us to make decisions on the basis of certain conditions. The conditions or constraints often take the form of inequalities. In this section, we will begin to formulate, analyze, and solve such problems, at a simple level, to understand the many components of such a problem.
A typical linear programming problem consists of finding an extreme value of a linear equation subject to certain constraints. We are either trying to maximize or minimize the value of this linear equation, such as to maximize profit or revenue, or to minimize cost. That is why these linear programming problems are classified as maximization or minimization problems, or just optimization problems. The value we are trying to optimize is called an objective function, and the conditions that must be satisfied are called constraints.
When we graph all constraints, the area of the graph that satisfies all constraints is called the feasible region. The Fundamental Theorem of Linear Programming states that the maximum (or minimum) value of the objective function always takes place at the vertices of the feasible region. We call these vertices critical points. These are found using any methods from Section 1.4 as we are looking for the points where any two of the boundary lines intersect.
A typical example is to maximize profit from producing several products, subject to limitations on materials or resources needed for producing these items; the problem requires us to determine the amount of each item produced. Another type of problem involves scheduling; we need to determine how much time to devote to each of several activities in order to maximize income from (or minimize cost of) these activities, subject to limitations on time and other resources available for each activity.
In this chapter, we will work with problems that involve only two variables, and therefore, can be solved by graphing. Here are the steps we'll follow:
The Maximization Linear Programming Problems
- Define the unknowns.
- Write the objective function that needs to be maximized.
- Write the constraints.
- For the standard maximization linear programming problems, constraints are of the form: \(ax + by ≤ c\)
- When the variables represent quantities that cannot be negative, we include the constraints: \(x ≥ 0\) and \(y ≥ 0\).
- Graph the constraints.
- Determine the feasible region.
- Find the corner points.
- Find the value of the objective function at each corner point to determine the corner point that gives the maximum value.
- State the answer to the original question.
Niki holds two part-time jobs, Job I and Job II. She never wants to work more than a total of 12 hours a week. She has determined that for every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation.
If Niki makes $40 an hour at Job I, and $30 an hour at Job II, how many hours should she work per week at each job to maximize her income?
Solution
- We start by defining our unknowns.
- Let the number of hours per week Niki will work at Job I = \(x\).
- Let the number of hours per week Niki will work at Job II = \(y\).
- Now we write the objective function. We're trying to maximize her income, so the equation will represent the calculation for finding her income. Since Niki gets paid $40 an hour at Job I, and $30 an hour at Job II, her total income I is given by the equation \[I = 40x + 30y \nonumber\]
- Our next task is to find the constraints. Each limitation in the problem will give a constraint.
- The second sentence in the problem states, "She never wants to work more than a total of 12 hours a week." This translates into the following constraint: \[x + y \leq 12 \nonumber \]
- The third sentence states, "For every hour she works at Job I, she needs 2 hours of preparation time, and for every hour she works at Job II, she needs one hour of preparation time, and she cannot spend more than 16 hours for preparation." Therefore the next constraint is \[2x + y \leq 16 \nonumber\]
- The fact that \(x\) and \(y\) can never be negative is represented by the following two constraints: \[x \geq 0 \text{, and } y \geq 0 \nonumber.\]
- In summary, our entire problem can be written as:
\[\begin{array}{ll}
\textbf { Maximize } & \mathrm{I}=40 \mathrm{x}+30 \mathrm{y} \\
\textbf { Subject to: } & \mathrm{x}+\mathrm{y} \leq 12 \\
& 2 \mathrm{x}+\mathrm{y} \leq 16 \\
& \mathrm{x} \geq 0 ; \mathrm{y} \geq 0
\end{array}\nonumber\]
- In order to solve the problem, we graph the constraints and shade the region that satisfies all the inequality constraints. Any appropriate method can be used to graph the lines for the constraints.
- Graph each inequality.
- When doing this by hand, refer to the strategies in Section 2.2.
- This may also be done in the Desmos app or on https://www.desmos.com/calculator. On a computer, the \( \leq \) symbol can be written by typing the \(<\) symbol followed by the \(=\) symbol.
- Determine which direction to shade for each line. There are three main strategies to decide how much shading is put on the graph:
- Strategy A: Graph all inequalities exactly as written. The negative of this method is that it is often difficult to see exactly which region is covered by all colors. In the graphic below, the feasible region is the darkest gray four-sided figure in the lower left portion of the graph.

- Strategy B: Graph ALMOST all inequalities, omitting \(x ≥ 0\) and \(y ≥ 0\). The feasible region will be slightly easier to identify, but the negative of this method is that students must remember that the feasible region actually stops at the axes.
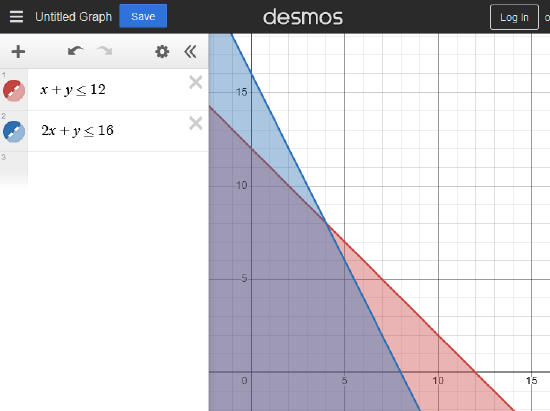
- Strategy C: Graph the OPPOSITE of each inequality. The feasible region will be clearly visible as the void or the white space between the graphs. The negative of this strategy is that it can be easy to make a mistake when typing in the inequalities, as they will be different than what is in the problem. Often students switch some inequalities but accidentally don't switch ALL inequalities.

- Strategy A: Graph all inequalities exactly as written. The negative of this method is that it is often difficult to see exactly which region is covered by all colors. In the graphic below, the feasible region is the darkest gray four-sided figure in the lower left portion of the graph.
- Graph each inequality.
- Determine the feasible region, which is the region that makes all inequalities true. No matter which strategy is used, the inequalities above should yield the feasible region shown below.
- Determine the corner points of the feasible region. These are known as the critical points or critical values.
- When graphing by hand, this can be done using any of the methods discussed in Section 1.3.
- When graphing in Desmos, this can be accomplished by clicking on the point of intersection.

- The Fundamental Theorem of Linear Programming states that the maximum (or minimum) value of the objective function always takes place at the vertices of the feasible region. Therefore, we will substitute these points in the objective function to see which point gives us the maximum value. In this case, we are looking for the highest income per week. We list the results below.
| Critical Points | Income = \(40x+30y\) |
|---|---|
| (0, 0) | I = 40(0) + 30(0) = $0 |
| (0, 12) | I = 40(0) + 30(12) = $360 |
| (4, 8) | I = 40(4) + 30(8) = $400 |
| (8, 0) | I = 40(8) + 30(0) = $320 |
8. The point (4, 8) gives the most profit: $400. Therefore, we conclude that Niki should work 4 hours at Job I, and 8 hours at Job II.
A factory manufactures two types of gadgets, regular and premium. Each gadget requires the use of two operations, assembly and finishing, and there are at most 12 hours available for each operation. A regular gadget requires 1 hour of assembly and 2 hours of finishing, while a premium gadget needs 2 hours of assembly and 1 hour of finishing. Due to other restrictions, the company can make at most 7 gadgets a day. If a profit of $20 is realized for each regular gadget and $30 for a premium gadget, how many of each should be manufactured to maximize profit?
Solution
1. We start by defining our unknowns:
- Let the number of regular gadgets manufactured each day = \(x\).
- and the number of premium gadgets manufactured each day = \(y\).
2. Now we write the objective function. We are trying to maximize profit, which will be $20 for however many regular gadgets we manufacture (\(x\) and $30 for however many premium gadgets we manufacture (\(y\). Therefore profit is is given by the equation
\[P = 20x + 30y \nonumber\]
3. We now write the constraints.
- The fourth sentence states that the company can make at most 7 total gadgets a day. This translates as
\[x + y \leq 7 \nonumber\]
- One limitation given is the hours for the assembly operation. Since the regular gadget requires one hour of assembly and the premium gadget requires two hours of assembly, and there are at most 12 hours available for this operation, we get
\[x + 2y \leq 12 \nonumber\]
- Similarly, we limited by the finishing operation. The regular gadget requires two hours of finishing and the premium gadget one hour. Again, there are at most 12 hours available for finishing. This gives us the following constraint.
\[2x + y \leq 12 \nonumber \]
- We are also limited by reality. The fact that \(x\) and \(y\) can never be negative is represented by the following two constraints:
\[x \geq 0 \text{, and } y \geq 0 \nonumber.\]
- In summary, our entire problem can be written as follows:
\[\begin{array}{ll}
\textbf { Maximize } & \mathrm{P}=20 \mathrm{x}+30 \mathrm{y} \\
\textbf { Subject to: } & \mathrm{x}+\mathrm{y} \leq 7 \\
& \mathrm{x}+2\mathrm{y} \leq 12 \\
& 2\mathrm{x} +\mathrm{y} \leq 12 \\
& \mathrm{x} \geq 0 ; \mathrm{y} \geq 0
\end{array} \nonumber\]
4. In order to solve the problem, we next graph each of the constraints.
By using Strategy A shown in the example above, we get a graph like this:

5. Determine the feasible region, which is the region that makes all inequalities true.

6. Determine the corner points of the feasible region.
- When graphing by hand, this can be done using any of the methods discussed in Section 1.3.
- When graphing in Desmos, this can be accomplished by clicking on the point of intersection.

7. We substitute these points in the objective function to see which point gives us the maximum profit each day. The results are listed below.
| Critical Point | Profit = \(20x + 30y\) |
|---|---|
| (0, 0) | P = 20(0) + 30(0) = $0 |
| (0, 6) | P = 20(0) + 30(6) = $180 |
| (2, 5) | P = 20(2) + 30(5) = $190 |
| (5, 2) | P = 20(5) + 30(2) = $160 |
| (6,0) | P = 20(6) + 30(0) = $120 |
8. The point (2, 5) gives the most profit, and that profit is $190. Therefore, we conclude that we should manufacture 2 regular gadgets and 5 premium gadgets daily to obtain the maximum profit of $190.
So far we have focused on “standard maximization problems” in which
- The objective function is to be maximized
- All constraints are of the form \(ax + by \leq c\)
- All variables are constrained to by non-negative (\(x ≥ 0\), \(y ≥ 0\))
We will next consider an example where that is not the case. Our next problem is said to have “mixed constraints”, since some of the inequality constraints are of the form \(ax + by ≤ c\) and some are of the form \(ax + by ≥ c\). The non-negativity constraints are still an important requirement in any linear program.
Solve the following maximization problem graphically.
\[\begin{array}{ll}
\textbf { Maximize } & \mathrm{Z}=10 \mathrm{x}+15 \mathrm{y} \\
\textbf { Subject to: } & \mathrm{x}+\mathrm{y} \geq 1 \\
& \mathrm{x}+2\mathrm{y} \leq 6 \\
& 2\mathrm{x} +\mathrm{y} \leq 6 \\
& \mathrm{x} \geq 0 ; \mathrm{y} \geq 0
\end{array} \nonumber\]
Solution
The graph is shown below.
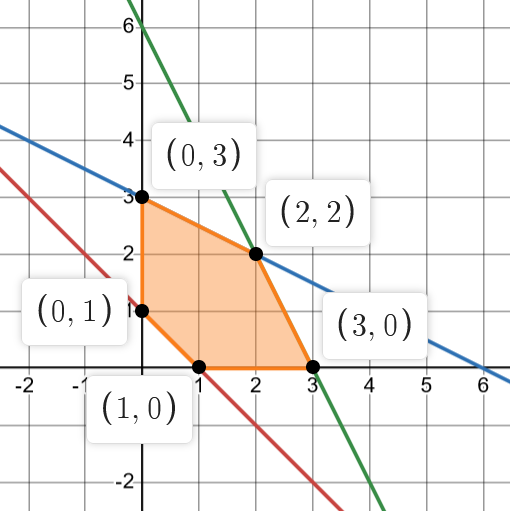
The five critical points are listed in the above figure.
| Critical point | Z = \(10x + 15y\) |
|---|---|
| (1, 0) | Z = 10(1) + 15(0) = 10 |
| (3, 0) | Z = 10(3) + 15(0) = 30 |
| (2, 2) | Z = 10(2) + 15(2) = 50 |
| (0, 3) | Z = 10(0) + 15(3) = 45 |
| (0,1) | Z = 10(0) + 15(1) = 15 |
The point (2, 2) maximizes the objective function to a maximum z-value of 50.
We summarize:
The Maximization Linear Programming Problems
- Define the unknowns.
- Write the objective function that needs to be maximized.
- Write the constraints.
- For the standard maximization linear programming problems, constraints are of the form: \(ax + by ≤ c\)
- Since the variables are non-negative, we include the constraints: \(x ≥ 0\); \(y ≥ 0\).
- Graph the constraints.
- Determine the feasible region.
- Find the corner points.
- Find the value of the objective function at each corner point to determine the corner point that gives the maximum value.
- State the answer to the original question.



