1.4: Solving Systems of Linear Equations in Two Variables
- Page ID
- 147276
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, you will learn to:
- Determine if a given ordered pair is a solution to a system of equations.
- Solve a system of linear equations in two variables by graphing, substitution, and elimination by addition.
- Find the equilibrium point when a demand and a supply equation are given.
- Find the break-even point when the revenue and the cost functions are given.
Before you get started, take this prerequisite quiz.
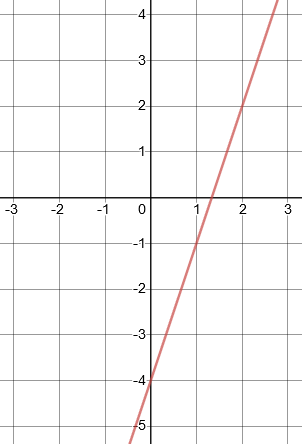
1. Graph all solutions to the equation \(y=3x-4\).
- Click here to check your answer
-
If you missed this problem, review Section 1.2. (Note that this will open in a new window.)
2. Graph all solutions to the equation \(3x-2y=12\).
- Click here to check your answer
-

If you missed this problem, review Section 1.2. (Note that this will open in a new window.)
3. Is \((2, 5)\) a solution to \(x-5y=2\)?
- Click here to check your answer
-
No, because \(-23 \neq 2\).
If you missed this problem, review Section 1.1. (Note that this will open in a new window.)
A skateboard manufacturer introduces a new line of boards. The manufacturer tracks its costs, which is the amount it spends to produce the boards, and its revenue, which is the amount it earns through sales of its boards. How can the company determine if it is making a profit with its new line? How many skateboards must be produced and sold before a profit is possible? In this section, we will consider linear equations with two variables to answer these and similar questions.

Solutions to Systems of Linear Equations
In order to investigate situations such as that of the skateboard manufacturer, we need to recognize that we are dealing with more than one variable and likely more than one equation. A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously.
To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
In this section, we will look at systems of linear equations in two variables, which consist of two equations that contain two different variables. For example, consider the following system of linear equations in two variables.
\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair \((4,7)\) is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly we will investigate methods of finding such a solution if it exists.
\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*}\]
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
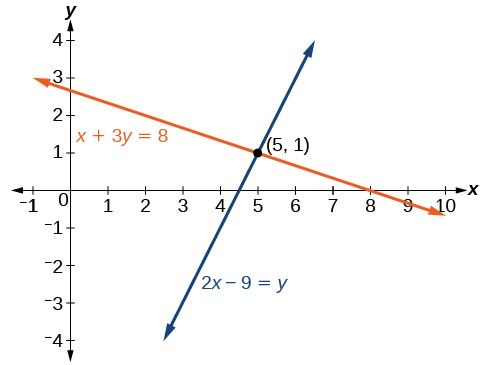
Determine whether the ordered pair \((5,1)\) is a solution to the given system of equations.
\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]
Solution
Substitute the ordered pair \((5,1)\) into both equations.
\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{ True} \end{align*}\]
The ordered pair \((5,1)\) satisfies both equations, so it is is the solution to the system.
Analysis
We can see the solution clearly by plotting the graph of each equation. Since the solution is an ordered pair that satisfies both equations, it is a point on both of the lines and thus the point of intersection of the two lines. See Figure \(\PageIndex{2}\).
Determine whether the ordered pair \((8,5)\) is a solution to the following system.
\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]
- Answer
-
Not a solution.
Generally, we aren't given the coordinates of a possible solution. Instead, we need to find it.
There are three main methods for finding a solution to a system of equations:
- Graphing,
- Substitution
- Elimination by addition
We'll work through each method below.
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
- Carefully and accurately graph each equation on the same set of axes.
- Identify the point at which the lines intersect.
- Check the solution in both equations.
- Write the soluiton as an ordered pair.
Solve the following system of equations by graphing.
\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]
Solution
Solve the first equation for \(y\).
\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]
Solve the same equation for \(y\).
\[\begin{align*} x−y &= −1 \\ &= x+1 \end{align*}\]
Graph both equations on the same set of axes as in Figure \(\PageIndex{3}\).
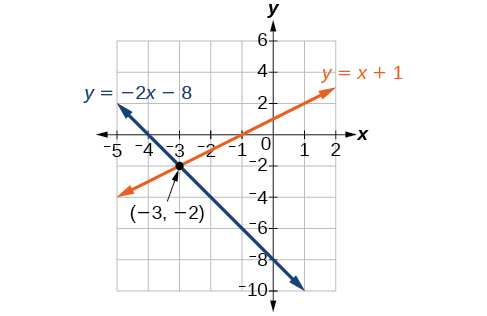
The lines appear to intersect at the point \((−3,−2)\). We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations.
\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 −8 \text{ True} \\ (−3)−(−2) &= −1 \\ −1 &= −1 \text{ True} \end{align*}\]
Solve the following system of equations by graphing.
\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]
- Answer
-
The solution to the system is the ordered pair \((−5,3)\).
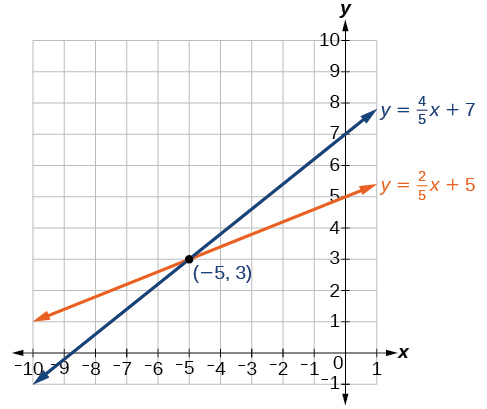
Figure \(\PageIndex{4}\)
Solving Systems of Equations by Substitution
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method method is solving a system of equations by the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable. Recall that we can solve for only one variable at a time, which is the reason the substitution method is both valuable and practical.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the other equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
- Write the solution as an ordered pair.
Solve the following system of equations by substitution.
\[\begin{align*} −x+y &= −5 \\ 2x−5y &= 1 \end{align*}\]
Solution
First, we will solve the first equation for \(y\).
\[\begin{align*} −x+y &=−5 \\ y &= x−5 \end{align*}\]
Now we can substitute the expression \(x−5\) for \(y\) in the second equation.
\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x &= 8 \end{align*}\]
Now, we substitute \(x=8\) into the first equation and solve for \(y\).
\[\begin{align*} −(8)+y &= −5 \\ y &= 3 \end{align*}\]
Our solution is \((8,3)\).
Check the solution by substituting \((8,3)\) into both equations.
\[\begin{align*} −x+y &= −5 \\ −(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8)−5(3) &= 1 \text{ True} \end{align*}\]
Solve the following following system of equations by substitution.
\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]
- Answer
-
\((−2,−5)\)
Solving Systems of Equations in Two Variables by the Elimination by Addition Method
A third method of solving systems of linear equations is the Addition by addition method of solving systems of linear equations is the addition method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.
- Write both equations with x- and y-variables on the left side of the equal sign and constants on the right. Write one equation above the other, lining up corresponding variables.
- If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
- Write the solution as an ordered pair.
Solve the given system of equations by elimination by addition.
\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]
Solution
Both equations are already set equal to a constant. Notice that the coefficient of \(x\) in the second equation, \(–1\), is the opposite of the coefficient of \(x\) in the first equation, \(1\). We can add the two equations to eliminate \(x\) without needing to multiply by a constant.
\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]
Now that we have eliminated \(x\), we can solve the resulting equation for \(y\).
\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]
Then, we substitute this value for \(y\) into one of the original equations and solve for \(x\).
\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ −x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]
The solution to this system is \(\left(−\dfrac{7}{3},\dfrac{2}{3}\right)\).
Check the solution in the first equation.
\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) &= -1\\ −\dfrac{7}{3}+\dfrac{4}{3} &= -1\\ −\dfrac{3}{3} &= −1\\ -1 &= −1 \;\;\;\;\;\;\;\; \text{True} \end{align*}\]
Analysis
We gain an important perspective on systems of equations by looking at the graphical representation. See Figure \(\PageIndex{5}\) to find that the equations intersect at the solution. We do not need to ask whether there may be a second solution because observing the graph confirms that the system has exactly one solution.
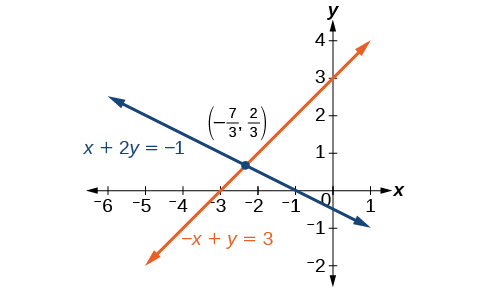
Solve the given system of equations by the elimination by addition method.
\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]
Solution
Adding these equations as presented will not eliminate a variable. However, we see that the first equation has \(3x\) in it and the second equation has \(x\). So if we multiply the second equation has \(x\). So if we multiply the second equation by \(−3\),the x-terms will add to zero.
\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Multiply both sides by }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Use the distributive property.} \end{align*}\]
Now, let’s add them.
\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{align*}\]
For the last step, we substitute \(y=−4\) into one of the original equations and solve for \(x\).
\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \end{align*}\]
Our solution is the ordered pair \((3,−4)\). See Figure \(\PageIndex{6}\). Check the solution in the original second equation.
\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\;\;\;\; \text{True} \end{align*}\]
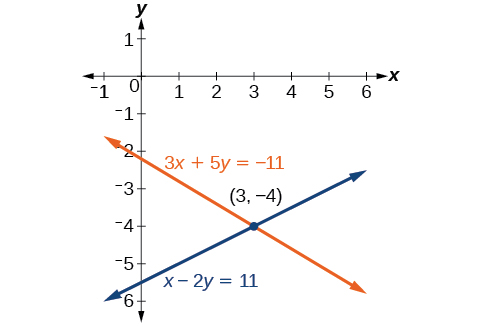
Solve the system of equations by elimination by addition.
\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]
- Answer
-
\((−6,−2)\)
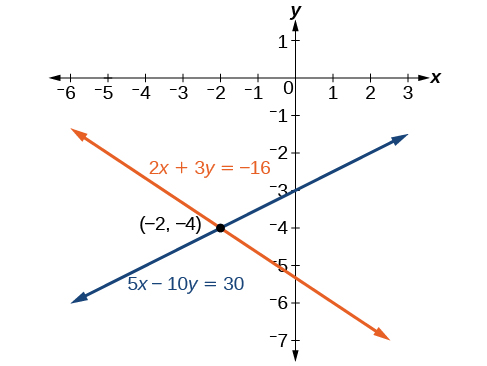
Solve the given system of equations in two variables by elimination by addition.
\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]
Solution
One equation has \(2x\) and the other has \(5x\). The least common multiple is \(10x\) so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate \(x\) by multiplying the first equation by \(−5\) and the second equation by \(2\).
\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x−20y &= 60 \end{align*}\]
Then, we add the two equations together.
\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align*}\]
Substitute \(y=−4\) into the original first equation.
\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*}\]
The solution is \((−2,−4)\). Check it in the other equation.
\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{align*}\]
See Figure \(\PageIndex{7}\).
SUPPLY, DEMAND AND THE EQUILIBRIUM PRICE
In a free market economy the supply curve for a commodity is the number of items of a product that can be made available at different prices, and the demand curve is the number of items the consumer will buy at different prices.
As the price of a product increases, its demand decreases and supply increases. On the other hand, as the price decreases the demand increases and supply decreases. The equilibrium price is reached when the demand equals the supply.
The supply curve for a product is \(y = 3.5x - 14\) and the demand curve for the same product is \(y = - 2.5x + 34\), where x is the price and y the number of items produced. Find the following.
- How many items will be supplied at a price of $10?
- How many items will be demanded at a price of $10?
- Determine the equilibrium price.
- How many items will be produced at the equilibrium price?
Solution
a) We substitute \(x = 10\) in the supply equation, \(y = 3.5x - 14\); the answer is \(y = 3.5(10) - 14 =21\).
b) We substitute \(x = 10\) in the demand equation, \(y = - 2.5x + 34\); the answer is \(y = - 2.5(10) + 34= 9\).
c) By letting the supply equal the demand, we get
\begin{aligned}
3.5x-140 &=-25x+340 \\
6x &=480 \\
x &=\$80
\end{aligned}
d) We substitute \(x = 8\) in either the supply or the demand equation; we get \(y = 14\).
The graph shows the intersection of the supply and the demand functions and their point of intersection, (8,14).
Interpretation: At equilibrium, the price is $8 per item, and 14 items are produced by suppliers and purchased by consumers.
Using Systems of Equations to Investigate Profits
Using what we have learned about systems of equations, we can return to the skateboard manufacturing problem at the beginning of the section. The skateboard manufacturer’s revenue function is the function used to calculate the amount the amount of money that comes into the business. It can be represented by the equation \(R=xp\), where \(x\)=quantity and \(p\)=price. The revenue function is shown in orange in Figure \(\PageIndex{11}\).
The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs, such as utilities. The cost function is shown in blue in Figure \(\PageIndex{11}\). The \(x\)-axis represents quantity in hundreds of units. The \(y\)-axis represents either cost or revenue in hundreds of dollars.
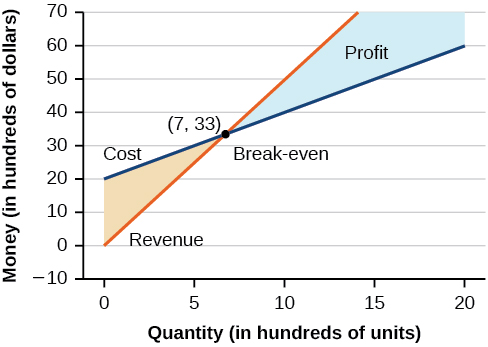
The point at which the two lines intersect is called the break-even point. We can see from the graph that if \(700\) units are produced, the cost is \($3,300\) and the revenue is also \($3,300\). In other words, the company breaks even if they produce and sell \(700\) units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to shaded region to the left represents quantities for which the company suffers a loss. The profit function is the revenue function minus the cost function, written as \(P(x)=R(x)−C(x)\). Clearly, knowing the quantity for which the cost equals the revenue is of great importance to businesses.
Given the cost function \(C(x)=0.85x+35,000\) and the revenue function function \(R(x)=1.55x\), find the break-even point and the profit function.
Solution
Write the system of equations using \(y\) to replace function notation.
\[\begin{align*} y &= 0.85x+35,000 \\ y &= 1.55x \end{align*}\]
Substitute the expression \(0.85x+35,000\) from the first equation into the second equation and solve for \(x\).
\[\begin{align*} 0.85x+35,000 &= 1.55x \\ 35,000 &= 0.7x \\ 50,000 &= x \end{align*}\]
Then, we substitute \(x=50,000\) into either the cost function or or the revenue function.
\(1.55(50,000)=77,500\)
The break-even is \((50,000,77,500)\).
The profit function is found using is formula formula \(P(x)=R(x)−C(x)\).
\[\begin{align*} P(x) &= 1.55x−(0.85x+35,000) \\ &=0.7x−35,000 \end{align*}\]
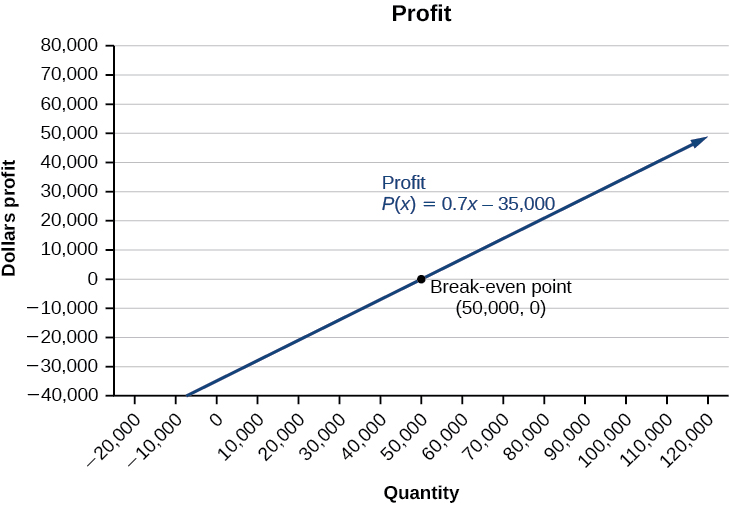
The profit function is \(P(x)=0.7x−35,000\).
Analysis
The cost to produce \(50,000\) units is \($77,500\), and the revenue from the sales of \(50,000\) units is also \($77,500\). To make a profit, the business must produce and sell more than \(50,000\) units. See Figure \(\PageIndex{12}\).
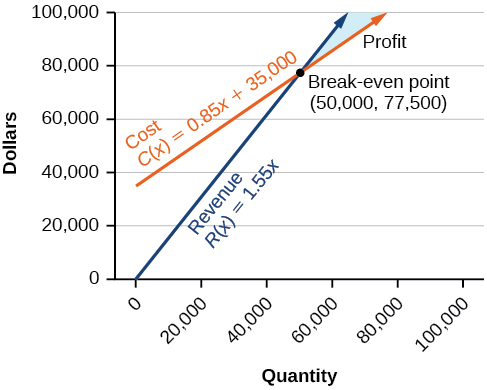
We see from the graph in Figure \(\PageIndex{13}\) that the profit function has a negative value until \(x=50,000\), when the graph crosses the \(x\)-axis. Then, the graph emerges into positive \(y\)-values and continues on this path as the profit function is a straight line. This illustrates that function is a straight line. This illustrates that the break-even point for businesses occurs when for businesses occurs when the profit function is \(0\). The area to the left of the break-even point represents operating at a loss.