2.1E: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercises
In Exercises 1 - 10, find both the point-slope form and the slope-intercept form of the line with the given slope which passes through the given point.
- m=3,P(3,−1)
- m=−2,P(−5,8)
- m=−1,P(−7,−1)
- m=23,P(−2,1)
- m=−15,P(10,4)
- m=17,P(−1,4)
- m=0,P(3,117)
- m=−√2,P(0,−3)
- m=−5,P(√3,2√3)
- m=678,P(−1,−12)
In Exercises 11 - 20, find the slope-intercept form of the line which passes through the given points.
- P(0,0),Q(−3,5)
- P(−1,−2),Q(3,−2)
- P(5,0),Q(0,−8)
- P(3,−5),Q(7,4)
- P(−1,5),Q(7,5)
- P(4,−8),Q(5,−8)
- P(12,34),Q(52,−74)
- P(23,72),Q(−13,32)
- P(√2,−√2),Q(−√2,√2)
- P(−√3,−1),Q(√3,1)
In Exercises 21 - 26, graph the function. Find the slope, y-intercept and x-intercept, if any exist.
- f(x)=2x−1
- f(x)=3−x
- f(x)=3
- f(x)=0
- f(x)=23x+13
- f(x)=1−x2
- Find all of the points on the line y=2x+1 which are 4 units from the point (-1, 3).
- Jeff can walk comfortably at 3 miles per hour. Find a linear function d that represents the total distance Jeff can walk in t hours, assuming he doesn’t take any breaks.
- Carl can stuff 6 envelopes per minute. Find a linear function E that represents the total number of envelopes Carl can stuff after t hours, assuming he doesn’t take any breaks.
- A landscaping company charges $45 per cubic yard of mulch plus a delivery charge of $20. Find a linear function which computes the total cost C (in dollars) to deliver x cubic yards of much.
- A plumber charges $50 for a service call plus $80 per hour. If she spends no longer than 8 hours a day at any one site, find a linear function that represents her total daily charges C (in dollars) as a function of time t (in hours) spent at any one given location.
- A salesperson is paid $200 per week plus 5% commission on her weekly sales of x dollars. Find a linear function that represents her total weekly pay, W (in dollars) in terms of x. What must her weekly sales be in order for her to earn $475.00 for the week?
- 33. An on-demand publisher charges $22.50 to print a 600 page book and $15.50 to print a 400 page book. Find a linear function which models the cost of a book C as a function of the number of pages p. Interpret the slope of the linear function and find and interpret C(0).
- The Topology Taxi Company charges $2.50 for the first fifth of a mile and $0.45 for each additional fifth of a mile. Find a linear function which models the taxi fare F as a function of the number of miles driven, m. Interpret the slope of the linear function and find and interpret F(0).
- Water freezes at 0∘ Celsius and 32∘ Fahrenheit and it boils at 100∘C and 212∘F.
- Find a linear function F that expresses temperature in the Fahrenheit scale in terms of degrees Celsius. Use this function to convert 20∘C into Fahrenheit.
- Find a linear function C that expresses temperature in the Celsius scale in terms of degrees Fahrenheit. Use this function to convert 110∘F into Celsius.
- Is there a temperature n such that F(n)=C(n)?
- Legend has it that a bull Sasquatch in rut will howl approximately 9 times per hour when it is 40∘F outside and only 5 times per hour if it’s 70∘F. Assuming that the number of howls per hour, N, can be represented by a linear function of temperature Fahrenheit, find the number of howls per hour he’ll make when it’s only 20∘F outside. What is the applied domain of this function? Why?
- Economic forces beyond anyone’s control have changed the cost function for PortaBoys to C(x)=105x+175. Rework Example 2.1.5 with this new cost function.
- In response to the economic forces in Exercise 37 above, the local retailer sets the selling price of a PortaBoy at $250. Remarkably, 30 units were sold each week. When the systems went on sale for $220, 40 units per week were sold. Rework Examples 2.1.6 and 2.1.7 with this new data. What difficulties do you encounter?
- A local pizza store offers medium two-topping pizzas delivered for $6.00 per pizza plus a $1.50 delivery charge per order. On weekends, the store runs a ‘game day’ special: if six or more medium two-topping pizzas are ordered, they are $5.50 each with no delivery charge. Write a piecewise-defined linear function which calculates the cost C (in dollars) of p medium two-topping pizzas delivered during a weekend.
- A restaurant offers a buffet which costs $15 per person. For parties of 10 or more people, a group discount applies, and the cost is $12.50 per person. Write a piecewise-defined linear function which calculates the total bill T of a party of n people who all choose the buffet.
- A mobile plan charges a base monthly rate of $10 for the first 500 minutes of air time plus a charge of 15¢ for each additional minute. Write a piecewise-defined linear function which calculates the monthly cost C (in dollars) for using m minutes of air time.
HINT: You may want to revisit Exercise 74 in Section 1.4.
- The local pet shop charges 12¢ per cricket up to 100 crickets, and 10¢ per cricket thereafter. Write a piecewise-defined linear function which calculates the price P, in dollars, of purchasing c crickets.
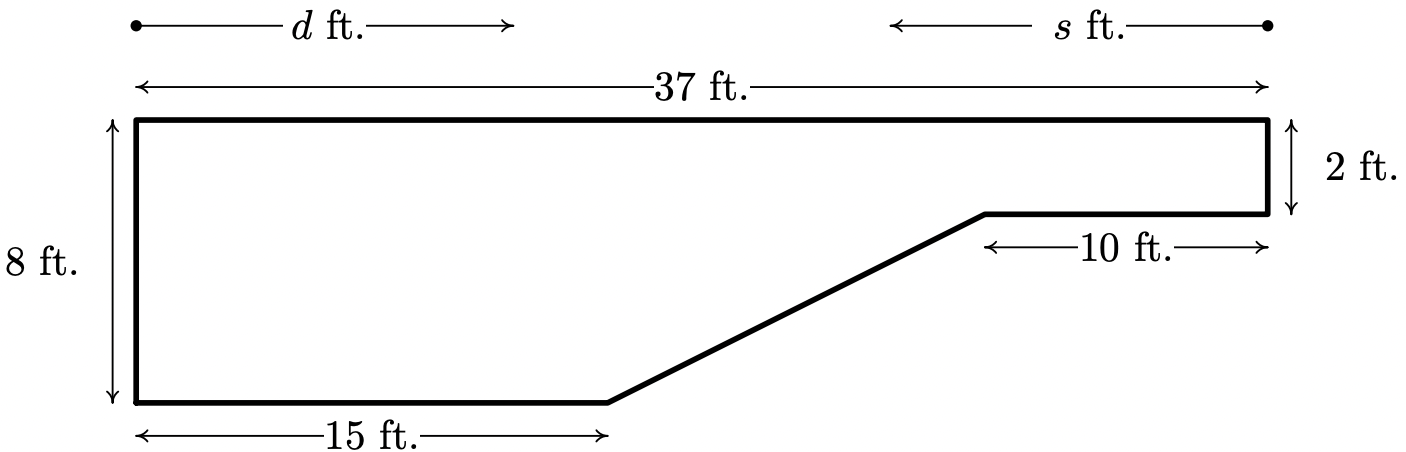
- The cross-section of a swimming pool is below. Write a piecewise-defined linear function which describes the depth of the pool, D (in feet) as a function of:
- the distance (in feet) from the edge of the shallow end of the pool, d.
- the distance (in feet) from the edge of the deep end of the pool, s.
- Graph each of the functions in (a) and (b). Discuss with your classmates how to transform one into the other and how they relate to the diagram of the pool.
In Exercises 44 - 49, compute the average rate of change of the function over the specified interval.
- f(x)=x3,[−1,2]
- f(x)=1x,[1,5]
- f(x)=√x,[0,16]
- f(x)=x2,[−3,3]
- f(x)=x+4x−3,[5,7]
- f(x)=3x2+2x−7,[−4,2]
In Exercises 50 - 53, compute the average rate of change of the given function over the interval [x,x+h]. Here we assume [x,x+h] is in the domain of the function.
- f(x)=x3
- f(x)=1x
- f(x)=x+4x−3
- f(x)=3x2+2x−7
- The height of an object dropped from the roof of an eight story building is modeled by: h(t)=−16t2+64,0≤t≤2. Here, h is the height of the object off the ground in feet, t seconds after the object is dropped. Find and interpret the average rate of change of h over the interval [0, 2].
- Using data from Bureau of Transportation Statistics, the average fuel economy F in miles per gallon for passenger cars in the US can be modeled by F(t)=−0.0076t2+0.45t+16, 0≤t≤28, where t is the number of years since 1980. Find and interpret the average rate of change of F over the interval [0, 28].
- The temperature T in degrees Fahrenheit t hours after 6 AM is given by:
T(t)=−12t2+8t+32,0≤t≤12
- Find and interpret T(4), T(8) and T(12).
- Find and interpret the average rate of change of T over the interval [4, 8].
- Find and interpret the average rate of change of T from t=8 to t=12.
- Find and interpret the average rate of temperature change between 10 AM and 6 PM.
- Suppose C(x)=x2−10x+27 represents the costs, in hundreds, to produce x thousand pens. Find and interpret the average rate of change as production is increased from making 3000 to 5000 pens.
- With the help of your classmates find several other “real-world” examples of rates of change that are used to describe non-linear phenomena.
(Parallel Lines) Recall from Intermediate Algebra that parallel lines have the same slope. (Please note that two vertical lines are also parallel to one another even though they have an undefined slope.) In Exercises 59 - 64, you are given a line and a point which is not on that line. Find the line parallel to the given line which passes through the given point.
- y=3x+2,P(0,0)
- y=−6x+5,P(3,2)
- y=23x−7,P(6,0)
- y=4−x3,P(1,−1)
- y=6,P(3,−2)
- x=1,P(−5,0)
(Perpendicular Lines) Recall from Intermediate Algebra that two non-vertical lines are perpendicular if and only if they have negative reciprocal slopes. That is to say, if one line has slope m1 and the other has slope m2 then m1⋅m2=−1. (You will be guided through a proof of this result in Exercise 71.) Please note that a horizontal line is perpendicular to a vertical line and vice versa, so we assume m1≠0 and m2≠0. In Exercises 65 - 70, you are given a line and a point which is not on that line. Find the line perpendicular to the given line which passes through the given point.
- y=13x+2,P(0,0)
- y=−6x+5,P(3,2)
- y=23x−7,P(6,0)
- y=4−x3,P(1,−1)
- y=6,P(3,−2)
- x=1,P(−5,0)
- We shall now prove that y=m1x+b1 is perpendicular to y=m2x+b2 if and only if m1⋅m2=−1. To make our lives easier we shall assume that m1>0 and m2<0. We can also “move” the lines so that their point of intersection is the origin without messing things up, so we’ll assume b1=b2=0. (Take a moment with your classmates to discuss why this is okay.) Graphing the lines and plotting the points O(0,0), P(1,m1) and Q(1,m2) gives us the following set up.
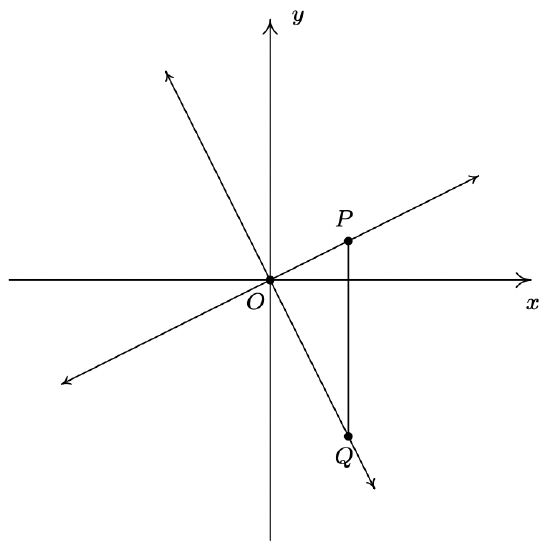
The line y=m1x will be perpendicular to the line y=m2x if and only if △OPQ is a right triangle. Let d1 be the distance from O to P, let d2 be the distance from O to Q and let d3 be the distance from P to Q. Use the Pythagorean Theorem to show that △OPQ is a right triangle if and only if m1⋅m2=−1 by showing d21+d22=d23 if and only if m1⋅m2=−1.
- Show that if a≠b, the line containing the points (a,b) and (b,a) is perpendicular to the line y=x. (Coupled with the result from Example 1.1.7, we have now shown that the line y=x is a perpendicular bisector of the line segment connecting (a,b) and (b,a). This means the points (a,b) and (b,a) are symmetric about the line y=x. We will revisit this symmetry in section 5.2.)
- The function defined by I(x)=x is called the Identity Function.
- Discuss with your classmates why this name makes sense.
- Show that the point-slope form of a line can be obtained from I using a sequence of the transformations defined in Section 1.7.
Answers
- y+1=3(x−3)y=3x−10
- y−8=−2(x+5)y=−2x−2
- y+1=−(x+7)y=−x−8
- y−1=23(x+2)y=23x+73
- y−4=−15(x−10)y=−15x+6
- y−4=17(x+1)y=17x+297
- y−117=0y=117
- y+3=−√2(x−0)y=−√2x−3
- y−2√3=−5(x−√3)y=−5x+7√3
- y+12=678(x+1)y=678x+666
- y=−53x
- y=−2
- y=85x−8
- y=94x−474
- y=5
- y=−8
- y=−54x+118
- y=2x+136
- y=−x
- y=√33x
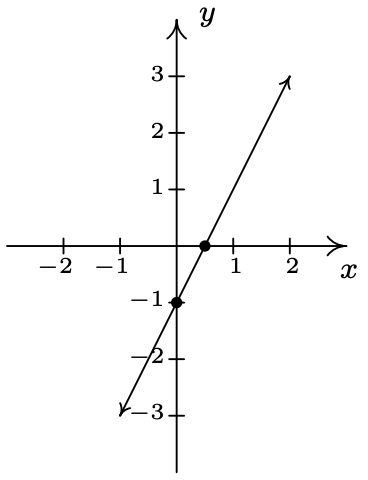
- f(x)=2x−1
slope: m=2
y-intercept: (0, −1)
x-intercept: (12,0)
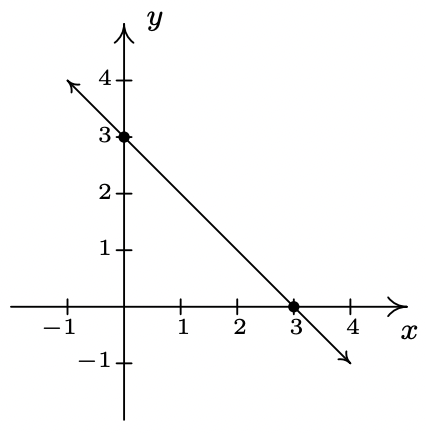
- f(x)=3−x
slope: m=−1
y-intercept: (0, 3)
x-intercept: (3, 0)
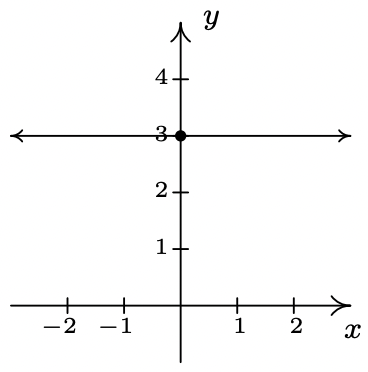
- f(x)=3
slope: m=0
y-intercept: (0, 3)
x-intercept: none
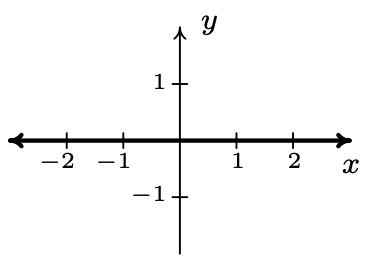
- f(x) = 0
slope: m=0
y-intercept: (0, 0)
x-intercept: {(x,0)|x is a real number }
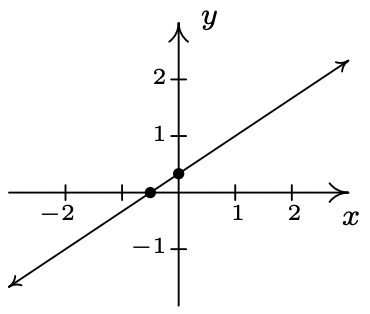
- f(x)=23x+13
slope: m=23
y-intercept: (0,13)
x-intercept: (−12,0)
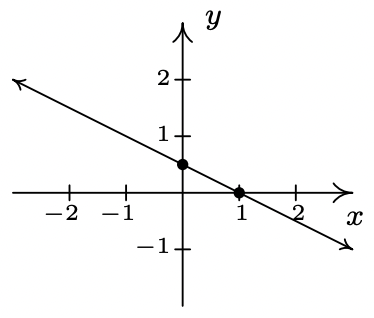
- f(x)=1−x2
slope: m=−12
y-intercept: (0,12)
x-intercept: (1,0)
- (−1,−1) and (115,275)
- d(t)=3t,t≥0
- E(t)=360t,t≥0
- C(x)=45x+20,x≥0
- C(t)=80t+50,0≤t≤8
- W(x)=200+.05x,x≥0 She must make $5500 in weekly sales
- C(p)=0.035p+1.5 The slope 0.035 means it costs 3.5¢ per page. C(0)=1.5 means there is a fixed, or start-up, cost of $1.50 to make each book.
- F(m)=2.25m+2.05 The slope 2.25 means it costs an additional $2.25 for each mile beyond the first 0.2 miles. F(0)=2.05, so according to the model, it would cost $2.05 for a trip of 0 miles. Would this ever really happen? Depends on the driver and the passenger, we suppose.
-
- F(C)=95C+32
- C(F)=59(F−32)=59F−1609
- F(−40)=−40=C(−40)
- N(T)=−215T+433 and N(20)=353≈12 howls per hour
Having a negative number of howls makes no sense and since N(107.5)=0 we can put an upper bound of 107.5∘F on the domain. The lower bound is trickier because there’s nothing other than common sense to go on. As it gets colder, he howls more often. At some point it will either be so cold that he freezes to death or he’s howling non-stop. So we’re going to say that he can withstand temperatures no lower than −60∘F so that the applied domain is [−60, 107.5].
- C(p)={6p+1.5 if 1≤p≤55.5p if p≥6
- T(n)={15n if 1≤n≤912.5n if n≥10
- C(m)={10 if 0≤m≤50010+0.15(m−500) if m>500
- P(c)={0.12c if 1≤c≤10012+0.1(c−100) if c>100
-
- D(d)={8 if 0≤d≤15−12d+312 if 15≤d≤272 if 27≤d≤37
- D(s)={2 if 0≤s≤1012s−3 if 10≤s≤228 if 22≤s≤37
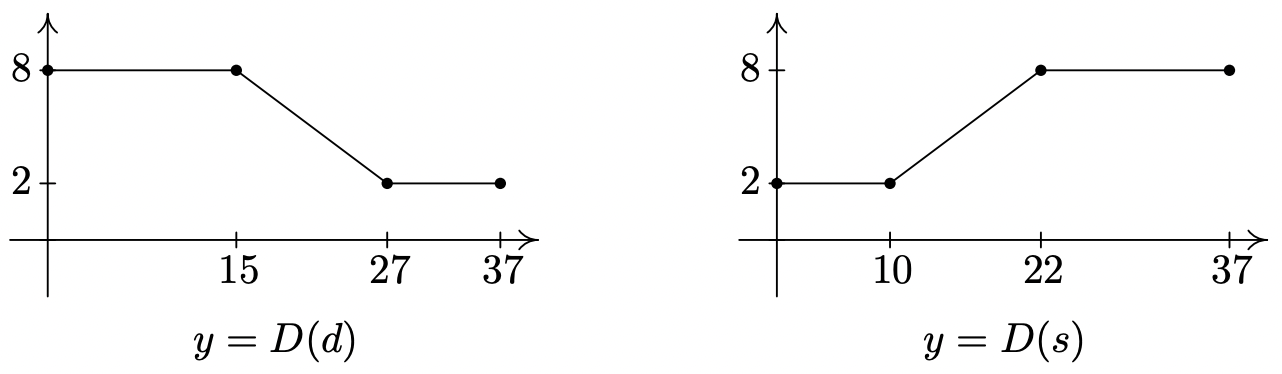
- 23−(−1)32−(−1)=3
- 15−115−1=−15
- √16−√016−0=14
- 32−(−3)23−(−3)=0
- 7+47−3−5+45−37−5=−78
- (3(2)2+2(2)−7)−(3(−4)2+2(−4)−7)2−(−4)=−4
- 3x2+3xh+h2
- −1x(x+h)
- −7(x−3)(x+h−3)
- 6x+3h+2
- The average rate of change is h(2)−h(0)2−0=−32. During the first two seconds after it is dropped, the object has fallen at an average rate of 32 feet per second. (This is called the average velocity of the object.)
- The average rate of change is F(28)−F(0)28−0=0.2372. During the years from 1980 to 2008, the average fuel economy of passenger cars in the US increased, on average, at a rate of 0.2372 miles per gallon per year.
-
- T(4)=56, so at 10 AM (4 hours after 6 AM), it is 56∘F. T(8)=64, so at 2 PM (8 hours after 6 AM), it is 64∘F. T(12)=56, so at 6 PM (12 hours after 6 AM), it is 56∘F.
- The average rate of change is T(8)−T(4)8−4=2. Between 10 AM and 2 PM, the temperature increases, on average, at a rate of 2∘F per hour.
- The average rate of change is T(12)−T(8)12−8=−2. Between 2 PM and 6 PM, the temperature decreases, on average, at a rate of 2∘F per hour.
- The average rate of change is T(12)−T(4)12−4=0. Between 10 AM and 6 PM, the temperature, on average, remains constant.
- The average rate of change is C(5)−C(3)5−3=−2. As production is increased from 3000 to 5000 pens, the cost decreases at an average rate of $200 per 1000 pens produced (20¢ per pen.)
- y=3x
- y=−6x+20
- y=23x−4
- y=−13x−23
- y=−2
- x=−5
- y=−3x
- y=16x+32
- y=−32x+9
- y=3x−4
- x=3
- y=0

