2.3E: Exercises

Exercises

In Exercises 1-9, graph the quadratic function. Find the \(x\)- and \(y\)-intercepts of each graph, if any exist. If it is given in general form, convert it into standard form; if it is given in standard form, convert it into general form. Find the domain and range of the function and list the intervals on which the function is increasing or decreasing. Identify the vertex and the axis of symmetry and determine whether the vertex yields a relative and absolute maximum or minimum.

1. \(f(x) = x^{2} + 2\)
2. \(f(x) = -(x + 2)^{2}\)
3. \(f(x) = x^{2} - 2x - 8\)
4. \(f(x) = -2(x + 1)^{2} + 4\)
5. \(f(x) = 2x^2 - 4x - 1\)
6. \(f(x) = -3x^{2} + 4x - 7\)
7. \(f(x) = x^2 + x + 1\)
8. \(f(x) = -3x^2+5x+4\)
9. \(f(x) = x^{2} - \dfrac{1}{100} x - 1\)

In Exercises 10-14, the cost and price-demand functions are given for different scenarios. For each scenario,

• Find the profit function \(P(x)\).
• Find the number of items which need to be sold in order to maximize profit.
• Find the maximum profit.
• Find the price to charge per item in order to maximize profit.
• Find and interpret break-even points.

10. The cost, in dollars, to produce \(x\) “I’d rather be a Sasquatch” T-Shirts is \(C(x) = 2x+26\), \(x \geq 0\) and the price-demand function, in dollars per shirt, is \(p(x) = 30 - 2x\), \(0 \leq x \leq 15\).
11. The cost, in dollars, to produce \(x\) bottles of \(100 \%\) All-Natural Certified Free-Trade Organic Sasquatch Tonic is \(C(x) = 10x+100\), \(x \geq 0\) and the price-demand function, in dollars per bottle, is \(p(x) = 35 - x\), \(0 \leq x \leq 35\).
12. The cost, in cents, to produce \(x\) cups of Mountain Thunder Lemonade at Junior’s Lemonade Stand is \(C(x) = 18x + 240\), \(x \geq 0\) and the price-demand function, in cents per cup, is \(p(x) = 90-3x\), \(0 \leq x \leq 30\).
13. The daily cost, in dollars, to produce \(x\) Sasquatch Berry Pies is \(C(x) = 3x + 36\), \(x \geq 0\) and the price-demand function, in dollars per pie, is \(p(x) = 12-0.5x\), \(0 \leq x \leq 24\).
14. The monthly cost, in hundreds of dollars, to produce \(x\) custom built electric scooters is \(C(x) = 20x + 1000\), \(x \geq 0\) and the price-demand function, in hundreds of dollars per scooter, is \(p(x) = 140-2x\), \(0 \leq x \leq 70\).
15. The International Silver Strings Submarine Band holds a bake sale each year to fund their trip to the National Sasquatch Convention. It has been determined that the cost in dollars of baking \(x\) cookies is \(C(x) = 0.1x + 25\) and that the demand function for their cookies is \(p = 10 - .01x.\) How many cookies should they bake in order to maximize their profit?
16. Using data from Bureau of Transportation Statistics, the average fuel economy \(\ F\) in miles per gallon for passenger cars in the US can be modeled by \(\ F(t)=-0.0076 t^{2}+0.45 t+16\), \(\ 0 \leq t \leq 28\), where \(\ t\) is the number of years since 1980. Find and interpret the coordinates of the vertex of the graph of \(\ y = F(t)\).
17. The temperature \(T\), in degrees Fahrenheit, \(t\) hours after 6 AM is given by: \[T(t) = -\frac{1}{2} t^2 + 8t+32, \quad 0 \leq t \leq 12\]
18. Suppose \(C(x) = x^2-10x+27\) represents the costs, in hundreds, to produce \(x\) thousand pens. How many pens should be produced to minimize the cost? What is this minimum cost?
19. Skippy wishes to plant a vegetable garden along one side of his house. In his garage, he found 32 linear feet of fencing. Since one side of the garden will border the house, Skippy doesn’t need fencing along that side. What are the dimensions of the garden which will maximize the area of the garden? What is the maximum area of the garden?
20. In the situation of Example 2.3.4, Donnie has a nightmare that one of his alpaca herd fell into the river and drowned. To avoid this, he wants to move his rectangular pasture away from the river. This means that all four sides of the pasture require fencing. If the total amount of fencing available is still 200 linear feet, what dimensions maximize the area of the pasture now? What is the maximum area? Assuming an average alpaca requires 25 square feet of pasture, how many alpaca can he raise now?
21. What is the largest rectangular area one can enclose with 14 inches of string?
22. The height of an object dropped from the roof of an eight story building is modeled by \(h(t) = -16t^2 + 64\), \(0 \leq t \leq 2\). Here, \(h\) is the height of the object off the ground, in feet, \(t\) seconds after the object is dropped. How long before the object hits the ground?
23. The height \(h\) in feet of a model rocket above the ground \(t\) seconds after lift-off is given by \(h(t) = -5t^2+100t\), for \(0 \leq t \leq 20\). When does the rocket reach its maximum height above the ground? What is its maximum height?
24. Carl’s friend Jason participates in the Highland Games. In one event, the hammer throw, the height \(h\) in feet of the hammer above the ground \(t\) seconds after Jason lets it go is modeled by \(h(t) = -16t^2 + 22.08t + 6\). What is the hammer’s maximum height? What is the hammer’s total time in the air? Round your answers to two decimal places.
25. Assuming no air resistance or forces other than the Earth’s gravity, the height above the ground at time \(t\) of a falling object is given by \(s(t) = -4.9t^{2} + v_0t + s_0\) where \(s\) is in meters, \(t\) is in seconds, \(v_0\) is the object’s initial velocity in meters per second and \(s_0\) is its initial position in meters.
    1. What is the applied domain of this function?
    2. Discuss with your classmates what each of \(v_0 > 0, \; v_0 = 0\) and \(v_0 < 0\) would mean.
    3. Come up with a scenario in which \(s_0 < 0\).
    4. Let’s say a slingshot is used to shoot a marble straight up from the ground \((s_0 = 0)\) with an initial velocity of 15 meters per second. What is the marble’s maximum height above the ground? At what time will it hit the ground?
    5. Now shoot the marble from the top of a tower which is 25 meters tall. When does it hit the ground?
    6. What would the height function be if instead of shooting the marble up off of the tower, you were to shoot it straight DOWN from the top of the tower?
26. The two towers of a suspension bridge are 400 feet apart. The parabolic cable attached to the tops of the towers is 10 feet above the point on the bridge deck that is midway between the towers. If the towers are 100 feet tall, find the height of the cable directly above a point of the bridge deck that is 50 feet to the right of the left-hand tower.
27. Graph \(f(x) = |1 - x^{2}|\)
28. Find all of the points on the line \(y=1-x\) which are \(2\) units from \((1,-1)\).
29. Let \(L\) be the line \(y = 2x+1\). Find a function \(D(x)\) which measures the distance squared from a point on \(L\) to \((0,0)\). Use this to find the point on \(L\) closest to \((0,0)\).
30. With the help of your classmates, show that if a quadratic function \(f(x) = ax^{2} + bx + c\) has two real zeros then the \(x\)-coordinate of the vertex is the midpoint of the zeros.

In Exercises 31-36, solve the quadratic equation for the indicated variable.

31. \(x^{2} - 10y^{2} = 0\) for \(x\)
32. \(y^{2} - 4y = x^{2} - 4\) for \(x\)
33. \(x^{2} - mx = 1\) for \(x\)
34. \(y^{2} - 3y = 4x\) for \(y\)
35. \(y^{2} - 4y = x^{2} - 4\) for \(y\)
36. \(-gt^{2} + v_0t + s_0 = 0\) for \(t\) (Assume \(g \neq 0\).)

Answers

1. \(f(x) = x^{2} + 2\) (this is both forms!)
   No \(x\)-intercepts
   \(y\)-intercept \((0, 2)\)
   Domain: \((-\infty, \infty)\)
   Range: \([2, \infty)\)
   Decreasing on \((-\infty, 0]\)
   Increasing on \([0, \infty)\)
   Vertex \((0, 2)\) is a minimum
   Axis of symmetry \(x = 0\)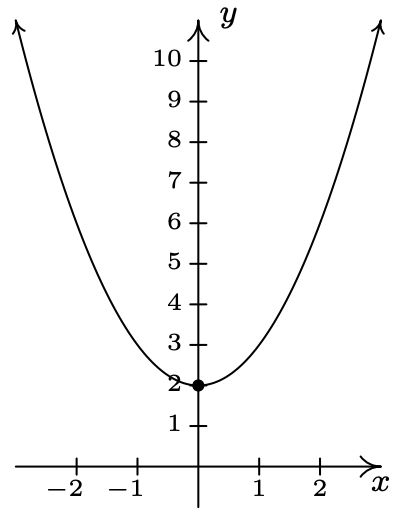

   

2. \(f(x) = -(x + 2)^{2} = -x^2-4x-4\)
   \(x\)-intercept \((-2, 0)\)
   \(y\)-intercept \((0, -4)\)
   Domain: \((-\infty, \infty)\)
   Range: \((-\infty, 0]\)
   Increasing on \((-\infty, -2]\)
   Decreasing on \([-2, \infty)\)
   Vertex \((-2, 0)\) is a maximum
   Axis of symmetry \(x = -2\)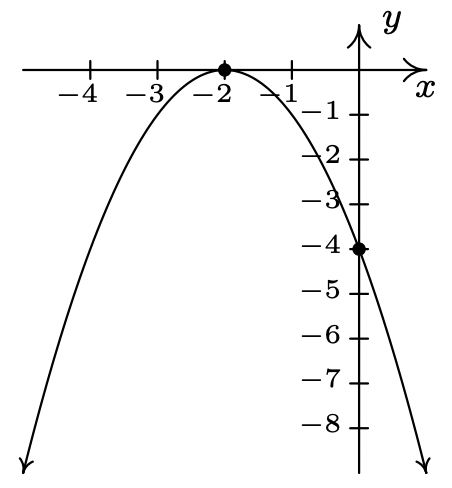

   

3. \(f(x) = x^{2} - 2x - 8 = (x - 1)^{2} - 9\)
   \(x\)-intercepts \((-2, 0)\) and \((4, 0)\)
   \(y\)-intercept \((0, -8)\)
   Domain: \((-\infty, \infty)\)
   Range: \([-9, \infty)\)
   Decreasing on \((-\infty, 1]\)
   Increasing on \([1, \infty)\)
   Vertex \((1, -9)\) is a minimum
   Axis of symmetry \(x = 1\)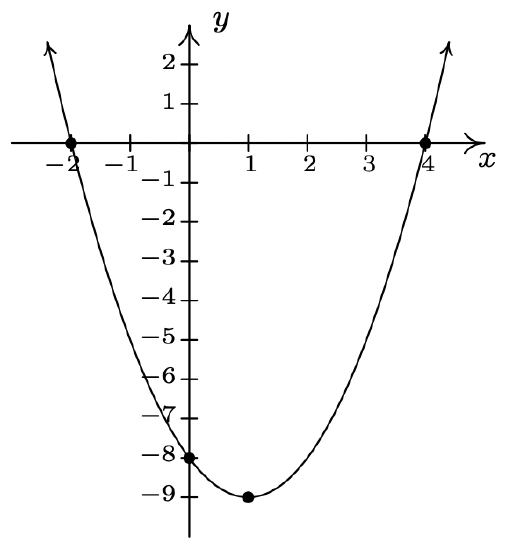

   

4. \(f(x) = -2(x + 1)^{2} + 4 = -2x^2-4x+2\)
   \(x\)-intercepts \((-1 - \sqrt{2}, 0)\) and \((-1 + \sqrt{2}, 0)\)
   \(y\)-intercept \((0, 2)\)
   Domain: \((-\infty, \infty)\)
   Range: \((-\infty, 4]\)
   Increasing on \((-\infty, -1]\)
   Decreasing on \([-1, \infty)\)
   Vertex \((-1, 4)\) is a maximum
   Axis of symmetry \(x = -1\)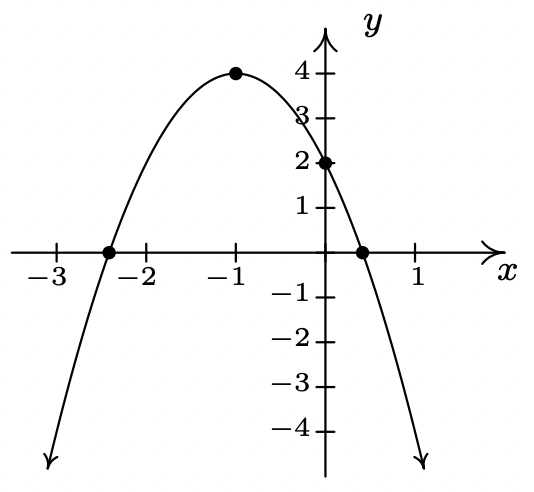

   

5. \(f(x) = 2x^2-4x-1 = 2(x-1)^2-3\)
   \(x\)-intercepts \(\left(\frac{2-\sqrt{6}}{2}, 0\right)\) and \(\left(\frac{2+\sqrt{6}}{2}, 0\right)\)
   \(y\)-intercept \((0, -1)\)
   Domain: \((-\infty, \infty)\)
   Range: \([-3, \infty)\)
   Increasing on \([1,\infty)\)
   Decreasing on \((-\infty,1]\)
   Vertex \((1, -3)\) is a minimum
   Axis of symmetry \(x = 1\)

   

6. \(f(x) = -3x^{2} + 4x - 7 = -3\left(x - \frac{2}{3} \right)^{2} - \frac{17}{3}\)
   No \(x\)-intercepts
   \(y\)-intercept \((0, -7)\)
   Domain: \((-\infty, \infty)\)
   Range: \(\left(-\infty, -\frac{17}{3}\right]\)
   Increasing on \(\left(-\infty, \frac{2}{3}\right]\)
   Decreasing on \(\left[\frac{2}{3}, \infty\right)\)
   Vertex \(\left(\frac{2}{3}, -\frac{17}{3}\right)\) is a maximum
   Axis of symmetry \(x = \frac{2}{3}\)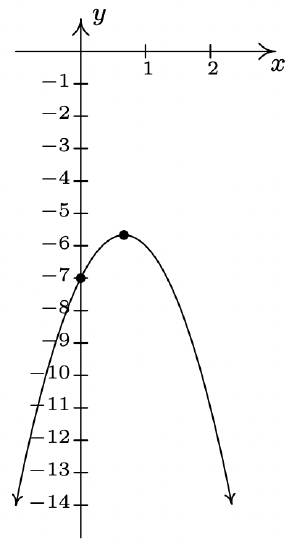

   

7. \(f(x) = x^2+x+1 = \left(x + \frac{1}{2}\right)^{2} + \frac{3}{4}\)
   No \(x\)-intercepts
   \(y\)-intercept \((0, 1)\)
   Domain: \((-\infty, \infty)\)
   Range: \(\left[ \frac{3}{4}, \infty\right)\)
   Increasing on \(\left[-\frac{1}{2}, \infty\right)\)
   Decreasing on \(\left(-\infty, -\frac{1}{2}\right]\)
   Vertex \(\left(-\frac{1}{2}, \frac{3}{4}\right)\) is a minimum
   Axis of symmetry \(x = -\frac{1}{2}\)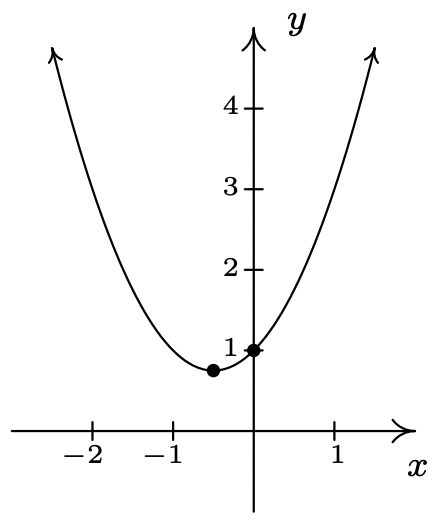

   

8. \(f(x) = -3x^2+5x+4 = -3\left(x-\frac{5}{6}\right)^2 + \frac{73}{12}\)
   \(x\)-intercepts \(\left(\frac{5 - \sqrt{73}}{6}, 0\right)\) and \(\left(\frac{5+\sqrt{73}}{6}, 0\right)\)
   \(y\)-intercept \((0, 4)\)
   Domain: \((-\infty, \infty)\)
   Range: \(\left(-\infty, \frac{73}{12} \right]\)
   Increasing on \(\left(-\infty, \frac{5}{6}\right]\)
   Decreasing on \(\left[ \frac{5}{6}, \infty\right)\)
   Vertex \(\left(\frac{5}{6}, \frac{73}{12} \right)\) is a maximum
   Axis of symmetry \(x = \frac{5}{6}\)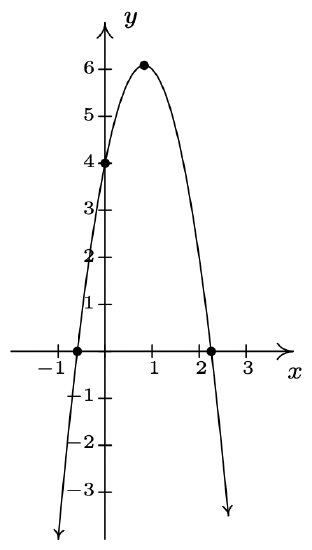

   

9. \(f(x) = x^{2} - \frac{1}{100} x - 1 = \left(x - \frac{1}{200}\right)^{2} - \frac{40001}{40000}\)
   \(x\)-intercepts \(\left(\frac{1 + \sqrt{40001}}{200}\right)\) and \(\left(\frac{1 - \sqrt{40001}}{200}\right)\)
   \(y\)-intercept \((0, -1)\)
   Domain: \((-\infty, \infty)\)
   Range: \(\left[-\frac{40001}{40000}, \infty \right)\)
   Decreasing on \(\left(-\infty, \frac{1}{200}\right]\)
   Increasing on \(\left[\frac{1}{200}, \infty \right)\)
   Vertex \(\left(\frac{1}{200}, -\frac{40001}{40000}\right)\) is a minimum¹²
   Axis of symmetry \(x = \frac{1}{200}\)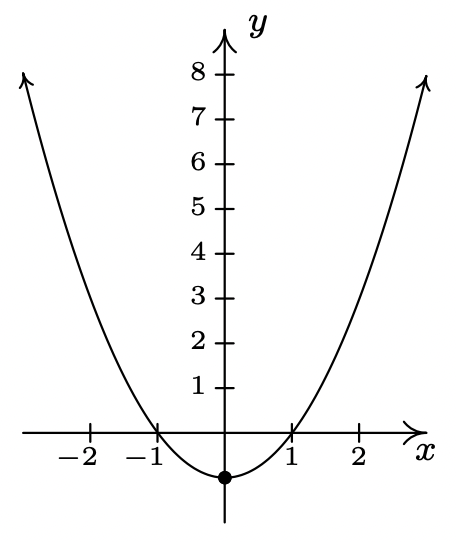

   

10. • \(P(x) = -2x^2+28x-26\), for \(0 \leq x \leq 15\).
    • \(7\) T-shirts should be made and sold to maximize profit.
    • The maximum profit is \(\$72\).
    • The price per T-shirt should be set at \(\$16\) to maximize profit.
    • The break even points are \(x=1\) and \(x=13\), so to make a profit, between 1 and 13 T-shirts need to be made and sold.
11. • \(P(x) = -x^2+25x-100\), for \(0 \leq x \leq 35\)
    • Since the vertex occurs at \(x=12.5\), and it is impossible to make or sell \(12.5\) bottles of tonic, maximum profit occurs when either \(12\) or \(13\) bottles of tonic are made and sold.
    • The maximum profit is \(\$56\).
    • The price per bottle can be either \(\$23\) (to sell 12 bottles) or \(\$22\) (to sell 13 bottles.) Both will result in the maximum profit.
    • The break even points are \(x=5\) and \(x=20\), so to make a profit, between 5 and 20 bottles of tonic need to be made and sold.
12. • \(P(x) = -3x^2+72x-240\), for \(0 \leq x \leq 30\)
    • \(12\) cups of lemonade need to be made and sold to maximize profit.
    • The maximum profit is \(192\)  or \(\$1.92\).
    • The price per cup should be set at \(54\)  per cup to maximize profit.
    • The break even points are \(x=4\) and \(x=20\), so to make a profit, between 4 and 20 cups of lemonade need to be made and sold.
13. • \(P(x) = -0.5 x^2+9x-36\), for \(0 \leq x \leq 24\)
    • \(9\) pies should be made and sold to maximize the daily profit.
    • The maximum daily profit is \(\$4.50\).
    • The price per pie should be set at \(\$7.50\) to maximize profit.
    • The break even points are \(x=6\) and \(x=12\), so to make a profit, between 6 and 12 pies need to be made and sold daily.
14. • \(P(x) = -2x^2+120x-1000\), for \(0 \leq x \leq 70\)
    • \(30\) scooters need to be made and sold to maximize profit.
    • The maximum monthly profit is \(800\) hundred dollars, or \(\$80,\!000\).
    • The price per scooter should be set at \(80\) hundred dollars, or \(\$8000\) per scooter.
    • The break even points are \(x=10\) and \(x=50\), so to make a profit, between 10 and 50 scooters need to be made and sold monthly.
15. 495 cookies
16. The vertex is (approximately) \((29.60, 22.66)\), which corresponds to a maximum fuel economy of 22.66 miles per gallon, reached sometime between 2009 and 2010 (29 – 30 years after 1980.) Unfortunately, the model is only valid up until 2008 (28 years after 1908.) So, at this point, we are using the model to predict the maximum fuel economy.
17. \(64^{\circ}\) at 2 PM (8 hours after 6 AM.)
18. 5000 pens should be produced for a cost of \(\$200\).
19. 8 feet by 16 feet; maximum area is 128 square feet.
20. 50 feet by 50 feet; maximum area is 2500 feet; he can raise 100 average alpacas.
21. The largest rectangle has area \(12.25\) square inches.
22. \(2\) seconds.
23. The rocket reaches its maximum height of \(500\) feet \(10\) seconds after lift-off.
24. The hammer reaches a maximum height of approximately \(13.62\) feet. The hammer is in the air approximately \(1.61\) seconds.
25. 1. The applied domain is \([0, \infty)\).
    2. The height function is this case is \(s(t) = -4.9t^{2} + 15t\). The vertex of this parabola is approximately \((1.53, 11.48)\) so the maximum height reached by the marble is \(11.48\) meters. It hits the ground again when \(t \approx 3.06\) seconds.
    3. The revised height function is \(s(t) = -4.9t^{2} + 15t + 25\) which has zeros at \(t \approx -1.20\) and \(t \approx 4.26\). We ignore the negative value and claim that the marble will hit the ground after \(4.26\) seconds.
    4. Shooting down means the initial velocity is negative so the height functions becomes \(s(t) = -4.9t^{2} - 15t + 25\).
26. Make the vertex of the parabola \((0, 10)\) so that the point on the top of the left-hand tower where the cable connects is \((-200, 100)\) and the point on the top of the right-hand tower is \((200, 100)\). Then the parabola is given by \(p(x) = \frac{9}{4000}x^{2} + 10\). Standing \(50\) feet to the right of the left-hand tower means you’re standing at \(x= -150\) and \(p(-150) = 60.625\). So the cable is 60.625 feet above the bridge deck there.
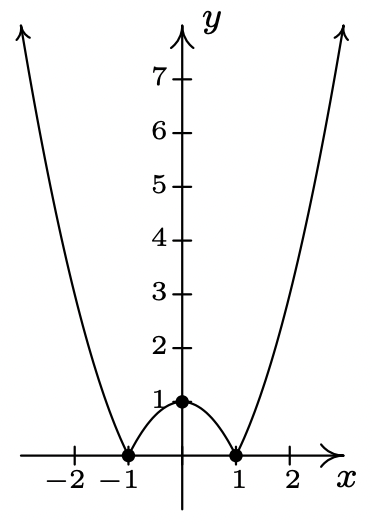
27. \(y = |1 -x^{2}|\)

    

28. \(\left(\dfrac{3 - \sqrt{7}}{2}, \dfrac{-1 + \sqrt{7}}{2} \right)\), \(\left(\dfrac{3 + \sqrt{7}}{2}, \dfrac{-1 - \sqrt{7}}{2} \right)\)
29. \(D(x) = x^2 + (2x+1)^2 = 5x^2+4x+1\), \(D\) is minimized when \(x=-\frac{2}{5}\), so the point on \(y=2x+1\) closest to \((0,0)\) is \(\left(-\frac{2}{5}, \frac{1}{5}\right)\)

31. \(x = \pm y\sqrt{10}\)
32. \(x = \pm (y - 2)\)
33. \(x = \dfrac{m \pm \sqrt{m^{2} + 4}}{2}\)
34. \(y = \dfrac{3 \pm \sqrt{16x + 9}}{2}\)
35. \(y = 2 \pm x\)
36. \(t = \dfrac{v_0 \pm \sqrt{v_0^{2} + 4gs_0}}{2g}\)