2.3: Introduction to Trigonometric Identities

Suggested Prerequisite Topics

This section is designed assuming you understand the following topics from Algebra.

• Simplifying compound rational expressions
• Performing arithmetic with rational expressions (addition, subtraction, multiplication, and division)

Learning Objectives

• Determine if an algebraic equation represents an identity.
• Find the value of a trigonometric function using the Reciprocal, Ratio, and Pythagorean Identities.

What is an Identity?

Recall that an equation may be true or false, depending on the values of any variables involved. For example, the equation\[x^2+3 x=10\nonumber \]is true only if \(x=2\) or \(x=-5\). An equation that is true only for certain variable values and false for others is called a conditional equation. When you solve a conditional equation, you find the variable values that make the equation true.

Some equations are true for all legitimate values of the variables. Such equations are called identities. Here are some examples of identities.\[\begin{array}{rcl}
3(x+y) & = & 3 x+3 y \\
(x+1)^2 & = & x^2+2 x+1 \\
\end{array} \nonumber \]In an identity, the statements on either side of the equal sign are called equivalent expressions because they have the same value for all values of the variable.

Definition: Identity

An identity is an equation that is true for all legitimate values of the variables.

Example \( \PageIndex{ 1 } \)

Which of the following equations are identities?

1. \(3 s+7 s=10 s\)
2. \(5 c(c-2 s)=5 c^2-10 c s\)
3. \(2 t-1=3\)

Solutions

Many of the algebraic operations you have already learned, such as combining like terms or applying the Distributive Law, produce equivalent expressions.

1. Equation (a) is an identity obtained by combining like terms on the left side.
2. Equation (b) is an identity obtained by applying the Distributive Law on the left side.
3. Equation (c) is not an identity because the equation is valid only for \(t=2\).

Checkpoint \( \PageIndex{ 1 } \)

Which of the following equations are identities?

1. \((c-s)(c+s)=c^2-s^2\)
2. \(3 t^2=1\)
3. \((2 c+1)+(s-3)=2 c+s-2\)

Answers

(a) and (c)

Of course, you wouldn’t be asked to solve an identity because all values of the variable are solutions. Instead, we use identities to replace one form of an expression with a more useful form. You do this when you solve a quadratic equation by factoring. For example,\[\begin{array}{rrclcr}
& 2 x^2-x-1 & = & 0 & \qquad & (\text{Factor the left side.}) \\
\implies & (2 x+1)(x-1) & = & 0 & & \\
\end{array}\nonumber \]Because \((2 x+1)(x-1)\) is equivalent to \(2 x^2-x-1\), we have not changed the equation or its solutions; however, we now can apply the Zero Factor Principle and solve the equation.

Using identities is especially useful when we are working with trigonometric ratios.

Using Trigonometric Ratios in Identities

Because the identity\[2 x^2-x-1=(2 x+1)(x-1)\nonumber \]is true for any value of \(x\), it is true when \(x\) is replaced, for instance, by \(\cos \left(\theta\right)\). This gives us a new identity\[2 \cos ^2 \left(\theta\right)-\cos \left(\theta\right)-1=\left(2 \cos \left(\theta\right)+1\right)\left(\cos \left(\theta\right)-1\right)\nonumber \]Expressions involving the trigonometric functions can be manipulated by the same rules that we use with simple variables (such as the Distributive Law or the Laws of Exponents).

Example \( \PageIndex{ 2 } \)

Which of the following equations are identities?

1. \(3 \sin \left(\theta\right)+7 \sin \left(\theta\right)=10 \sin\left( \theta\right)\)
2. \(5 \cos \left(\theta\right)\left(\cos \left(\theta\right)-2 \sin \left(\theta\right)\right)=5 \cos^2 \left(\theta\right)-10 \cos\left( \theta \right) \sin \left(\theta\right)\)
3. \(2 \tan \left(\theta\right)-1=3\)

Solutions

These equations are obtained from the equations in Example \( \PageIndex{ 1 } \) by replacing the variable \(s\) with \(\sin \left(\theta\right)\), the variable \(c\) with \(\cos \left(\theta\right)\), and the variable \(t\) with \(\tan \left(\theta\right)\). Equations (a) and (b) are identities, and equation (c) is not, for the same reasons as before.

Checkpoint \( \PageIndex{ 2 } \)

Which of the following equations are identities?

1. \(\left(\cos \left(\theta\right)-\sin \left(\theta\right)\right)\left(\cos \left(\theta\right)+\sin \left(\theta\right)\right)=\cos ^2 \left(\theta\right)-\sin ^2 \left(\theta\right)\)
2. \(3 \tan ^2 \left(\theta\right)=1\)
3. \(\left(2 \cos \left(\theta\right)+1\right)+\left(\sin \left(\theta\right)-3\right)=2 \cos \left(\theta\right)+\sin \left(\theta\right)-2\)

Answers

(a) and (c)

Caution: Examples are Not Proofs

To show that an equation is not an identity, we need only find one value of the variable for which the equation is false. However, to show that a given equation is an identity, it is not enough to show that the equation is valid for one, or even a dozen, values of the variable. The equation must be true for all legitimate values of the variable. Because we cannot check all values of the variable numerically, we must use algebraic methods to prove that an equation is an identity.

Ratio Identities

All of the trigonometric functions are related. We begin by considering the relationship between the tangent and the sine and cosine functions (we will find a similar relationship for the cotangent). Complete the following table with exact values.

\(\theta\)	\(\cos \left(\theta\right)\)	\(\sin \left(\theta\right)\)	\(\dfrac{\sin \left(\theta\right)}{\cos \left(\theta\right)}\)	\(\tan \left(\theta\right)\)
\(0^{\circ}\)
\(30^{\circ}\)
\(45^{\circ}\)
\(60^{\circ}\)

For the angles in the table,\[\tan \left(\theta\right)=\dfrac{\sin \left(\theta\right)}{\cos \left(\theta\right)}\nonumber \]The question you should have is, "Is this true for all angles?"

The short answer is no, but before we describe why, let's understand why this relationship exists between the tangent, sine, and cosine.

The sine function for an angle \( \theta \) is defined as \( \sin\left( \theta \right) = \frac{y}{r} \), where \( \left( x,y \right) \) is any point on the terminal side of \( \theta \) (other than the origin) and \( r = \sqrt{x^2 + y^2} \). Likewise, the cosine is defined to be \( \cos\left( \theta \right) = \frac{x}{r} \). If we look at the ratio of the sine to the cosine, we get\[ \dfrac{\sin\left( \theta \right)}{\cos\left( \theta \right)} = \dfrac{y/r}{x/r} = \dfrac{(y/r)}{(x/r)} \cdot \dfrac{r}{r} = \dfrac{(y/\cancel{r})}{(x/\cancel{r})} \cdot \dfrac{\cancel{r}}{\cancel{r}} = \dfrac{y}{x} = \tan\left( \theta \right). \nonumber \]A similar argument shows that\[ \cot\left( \theta \right) = \dfrac{\cos\left( \theta \right)}{\sin\left( \theta \right)}. \nonumber \]

One essential item to note, however, is that because \(\cos \left(90^{\circ}\right)=0\), the quotient \(\frac{\sin \left(\theta\right)}{\cos \left(\theta\right)}\) is undefined for \(\theta=90^{\circ}\), and, as such, \(\tan \left(90^{\circ}\right)\) is undefined. The same applies to for \(\theta=270^{\circ}\). For all other angles between \(0^{\circ}\) and \(360^{\circ}, \tan \left(\theta\right)=\frac{\sin \left(\theta\right)}{\cos \left(\theta\right)}\). A similar argument shows that \( \cot\left( 0^{ \circ } \right) \) and \( \cot\left( 180^{ \circ } \right) \) are undefined.

We are now ready to formalize these statements as a theorem.

Theorem: Ratio Identities

For any angle not coterminal with \(90^{\circ}\) or \(270^{\circ}\),\[\tan \left(\theta\right)=\dfrac{\sin \left(\theta\right)}{\cos \left(\theta\right)}.\nonumber \]For any angle not coterminal with \(0^{\circ}\) or \(180^{\circ}\),\[\cot \left(\theta\right)=\dfrac{\cos \left(\theta\right)}{\sin \left(\theta\right)}\nonumber \]

Advice: Memorize These Identities

The Ratio Identities are needed throughout the rest of Mathematics, Science, and Engineering. The need to commit them to memory and their importance cannot be overstated.

Example \( \PageIndex{ 3 } \)

If \( \sin\left( \theta \right) = \frac{12}{13} \) and \( \cos\left( \theta \right) = -\frac{5}{13} \), find the values of \( \tan\left( \theta \right) \) and \( \cot\left( \theta \right) \).

Solution

We apply the Ratio Identities to obtain\[\begin{array}{rcl}
\tan \left(\theta\right) & = & \dfrac{\sin \left(\theta\right)}{\cos \left(\theta\right)} \\
& = & \dfrac{12/13}{-5/13} \\
& = & \dfrac{12/13}{-5/13} \cdot \dfrac{13}{13} \\
& = & \dfrac{12}{-5} \\
& = & -\dfrac{12}{5} \\
\end{array} \nonumber \]and\[\begin{array}{rcl}
\cot \left(\theta\right) & = & \dfrac{\cos \left(\theta\right)}{\sin \left(\theta\right)} \\
& = & \dfrac{-5/13}{12/13} \\
& = & \dfrac{-5/13}{12/13} \cdot \dfrac{13}{13} \\
& = & \dfrac{-5}{12} \\
& = & -\dfrac{5}{12} \\
\end{array} \nonumber \]

Checkpoint \( \PageIndex{ 3 } \)

If \( \sin\left( \theta \right) = -\frac{1}{5} \) and \( \cos\left( \theta \right) = -\frac{2\sqrt{6}}{5} \), find the values of \( \tan\left( \theta \right) \) and \( \cot\left( \theta \right) \).

Answer

\(\tan\left( \theta \right) = \frac{1}{2\sqrt{6}}\) and \( \cot\left( \theta \right) = 2\sqrt{6} \)

Reciprocal Identities

We now state one of the more obvious identities. We find the following relationships by comparing the definitions of cosecant, secant, and cotangent to the three fundamental trigonometric functions (sine, cosine, and tangent).

Theorem: Reciprocal Identities

\[ \begin{array}{rclclcrclcl}
\sin\left( \theta \right) & = & \dfrac{1}{\csc\left( \theta \right)} & \quad & (\text{provided } \csc\left( \theta \right) \neq 0) & \qquad & \csc\left( \theta \right) & = & \dfrac{1}{\sin\left( \theta \right)} & \quad & (\text{provided } \sin\left( \theta \right) \neq 0) \\
\cos\left( \theta \right) & = & \dfrac{1}{\sec\left( \theta \right)} & \quad & (\text{provided } \sec\left( \theta \right) \neq 0) & \qquad & \sec\left( \theta \right) & = & \dfrac{1}{\cos\left( \theta \right)} & \quad & (\text{provided } \cos\left( \theta \right) \neq 0) \\
\tan\left( \theta \right) & = & \dfrac{1}{\cot\left( \theta \right)} & \quad & (\text{provided } \cot\left( \theta \right) \neq 0) & \qquad & \cot\left( \theta \right) & = & \dfrac{1}{\tan\left( \theta \right)} & \quad & (\text{provided } \tan\left( \theta \right) \neq 0) \\
\end{array} \nonumber \]

You likely already figured out the Reciprocal Identities because, for example, \( \sin\left( \theta \right) = \frac{y}{r} \) and \( \csc\left( \theta \right) = \frac{r}{y} \) are obvious reciprocals.

Advice: Memorize These Identities

The Reciprocal Identities are needed throughout the rest of Mathematics, Science, and Engineering. The need to commit them to memory and their importance cannot be overstated.

Example \(\PageIndex{4}\)

Compute \( \cos\left( \theta \right) \) given \( \sec\left( \theta \right) = -\frac{10}{3}\).

Solution

\( \cos\left( \theta \right) = \dfrac{1}{\sec\left( \theta \right)} = \dfrac{1}{-10/3} = -\dfrac{3}{10} \)

Checkpoint \(\PageIndex{4}\)

If \( \cot\left( \theta \right) = \frac{8}{5} \), find \( \tan\left( \theta \right) \).

Answer

\( \tan\left( \theta \right) = \frac{5}{8} \)

Caution: Cosecant, Secant, and Cotangent are NOT Inverses

Refrain from calling the cosecant, secant, and cotangent inverse trigonometric ratios. The word "inverse" is very special in this and future math courses. While it is true that \( \sin\left( \theta \right) \) and \( \csc\left( \theta \right) \) are multiplicative inverses, they are not functional inverses.

Pythagorean Identities

All of the trigonometric functions are related. We begin by considering the relationship between \(\sin \left(\theta\right)\) and \(\cos \left(\theta\right)\). Complete the following table with exact values.

\(\theta\)	\(\cos \left(\theta\right)\)	\(\sin \left(\theta\right)\)	\(\cos^2 \left(\theta\right)\)	\(\sin^2 \left(\theta\right)\)	\(\cos^2 \left(\theta\right) + \sin^2 \left(\theta\right)\)
\(0^{\circ}\)
\(30^{\circ}\)
\(45^{\circ}\)
\(60^{\circ}\)
\(90^{\circ}\)

For all the angles in the table,\[\cos ^2 \theta+\sin ^2 \theta=1.\nonumber \]However, we have only shown this is true for the angles in the table. What about all other angles?

From the coordinate definition of the trigonometric functions, we know that \( r = \sqrt{x^2 + y^2} \). Starting with this, we can prove the result from our table as follows:\[\begin{array}{rrclcr}
& r & = & \sqrt{x^2 + y^2} & \quad & \\
\\
\implies & r^2 & = & x^2 + y^2 & \quad & (\text{Squaring both sides}) \\
\\
\implies & 1 & = & \dfrac{x^2}{r^2} + \dfrac{y^2}{r^2} & \quad & (\text{Dividing both sides by }r^2) \\
\\
\implies & 1 & = & \left( \dfrac{x}{r} \right)^2 + \left( \dfrac{y}{r} \right)^2 & \quad & (\text{Laws of Exponents}) \\
\\
\implies & 1 & = & \left( \cos\left( \theta \right) \right)^2 + \left( \sin\left( \theta \right) \right)^2 & \quad & (\text{Definitions of the cosine and sine functions}) \\
\\
\implies & 1 & = & \cos^2\left( \theta \right) + \sin^2\left( \theta \right) & \quad & (\text{Using a better notation}) \\
\end{array} \nonumber \]

This is the most important result in all of Trigonometry.

Theorem: The Pythagorean Identity

For any angle \(\theta\),\[\cos^2 \left(\theta\right)+\sin^2 \left(\theta\right)=1.\nonumber \]

From its name, the Pythagorean Identity is intimately related to the Pythagorean Theorem.

Advice: Memorize This Identity

The Pythagorean Identity (also known as the Fundamental Pythagorean Identity) is needed throughout the rest of Mathematics. The need to commit this to memory and its importance cannot be overstated.

Example \( \PageIndex{ 5} \)

Evaluate \(\cos ^2\left(27^{\circ}\right)+\sin ^2\left(27^{\circ}\right)\) without using a calculator.

Solution

Because the Pythagorean Identity, \(\cos ^2 \left(\theta\right)+\sin ^2 \left(\theta\right)=1\), is true for any value of \(\theta\), it is true in particular for \(\theta=27^{\circ}\). So \(\cos ^2\left(27^{\circ}\right)+\sin ^2\left(27^{\circ}\right)=1\).

Checkpoint \( \PageIndex{ 5} \)

Evaluate \(5\left[\cos ^2\left(12^{\circ}\right)+\sin ^2\left(12^{\circ}\right)\right] \) without using a calculator.

Answer

5

When we solve more complicated trigonometric equations in later chapters, we will need to simplify trigonometric expressions so that they involve only one of the trigonometric functions. The Pythagorean Identity is useful when we wish to write an equivalent expression for either \(\cos ^2 \left(\theta\right)\) or for \(\sin ^2 \left(\theta\right)\). The following equivalent forms to the Pythagorean Identity will be helpful throughout Trigonometry.

Corollary: Alternate Forms of the Pythagorean Identity

\[\begin{array}{rclcrcl}
\sin ^2 \left(\theta\right) & = & 1-\cos ^2 \left(\theta\right) & \implies & \sin\left( \theta \right) & = & \pm \sqrt{1 - \cos^2\left( \theta \right)} \\
\cos ^2 \left(\theta\right) & = & 1-\sin ^2 \left(\theta\right) & \implies & \cos\left( \theta \right) & = & \pm \sqrt{1 - \sin^2\left( \theta \right)} \\
\end{array} \nonumber \]

The Pythagorean Identity, along with the Ratio and Reciprocal Identities, show us that all trigonometric functions of an angle are related. If we know the value of one trigonometric function at \( \theta \) and where \( \theta \) terminates, we can calculate the remaining trigonometric functions. We do not need to find the angle itself to do this. We only need to know which quadrant the angle lies in to determine the correct sign for the trigonometric ratios.

Advice: Memorize These Identities

The alternate forms of the Pythagorean Identity are needed throughout the rest of Mathematics, Science, and Engineering. While not as prevalent as the Pythagorean Theorem or the Quadratic Formula, the need to commit them to memory and their importance cannot be overstated.

Example \( \PageIndex{ 6} \) shows that we do not need to memorize the alternate forms of the Pythagorean Identity as long as we are confident manipulating mathematical expressions.

Example \( \PageIndex{ 6} \)

If \(\sin \left(\theta\right)=\frac{7}{25}\) and \(90^{\circ}<\theta<180^{\circ}\), find \(\cos \left(\theta\right)\) and \(\tan \left(\theta\right)\).

Solution

We substitute \(\sin \left(\theta\right)=\frac{7}{25}\) into the Pythagorean Identity \(\cos ^2 \left(\theta\right)+\sin ^2 \left(\theta\right)=1\) to get\[ \begin{array}{rrclcr}
& \cos ^2 \left(\theta\right)+\left(\dfrac{7}{25}\right)^2 & = & 1 & \quad & (\text{Substitute in } \dfrac{7}{25} \text{ for } \sin\left( \theta \right)) \\
\\
\implies & \cos ^2 \left(\theta\right) & = & 1-\left(\dfrac{7}{25}\right)^2 & \quad & (\text {Isolate } \cos ^2 \left(\theta\right)) \\
\\
\implies & \cos^2\left( \theta \right) & = & 1 - \dfrac{49}{625} & \quad & \\
\\
\implies & \cos^2\left( \theta \right) & = & \dfrac{576}{625} & \quad & \\
\\
\implies & \cos\left(\theta\right) & = & \pm \sqrt{\dfrac{576}{625}} & \quad & (\text {Take square roots of both sides}) \\
\\
\implies & \cos \left(\theta\right) & = & \pm \dfrac{24}{25} & \quad & \\
\\
\end{array} \nonumber \]Because \(\theta\) is between \(90^{\circ}\) and \(180^{\circ}\), \(\cos \left(\theta\right)\) must be negative. Therefore, \(\cos \left(\theta\right)=-\frac{24}{25}\). To find \(\tan \theta\), we use the Ratio Identities to get\[\tan \left(\theta\right)=\dfrac{\sin \left(\theta\right)}{\cos \left(\theta\right)}=\dfrac{7/25}{-24/25}= - \dfrac{7}{24}.\nonumber \]

We could have solved Example \( \PageIndex{ 6} \) by creating a quick sketch of \( \theta \) terminating in \( \mathrm{QII} \). Because \(\sin \left(\theta\right)=\frac{7}{25}\), we can choose a point on the terminal side to have \(y\)-coordinate 7 and \(r=25\) (see Figure \( \PageIndex{ 1 } \) below).

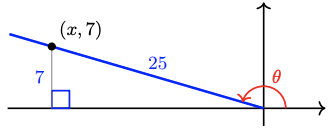
Figure \( \PageIndex{ 1 } \)

In order to calculate \(\cos \left(\theta\right)\) and \(\tan\left( \theta\right)\), we must find the \(x\)-coordinate of the point. By the Pythagorean Theorem,\[\begin{array}{rrclcr}
& x^2+7^2 & = & 25^2 & \quad & \\
\implies & x^2 & = & 576 & \quad & (\text{Isolating }x^2) \\
\implies & x & = & -24 & \quad & (\text{Taking square roots}) \\
\end{array} \nonumber \]Note that \(x\) is negative because the point \((x, 7)\) is in the second quadrant. Then\[\cos \left(\theta\right)=\dfrac{x}{r}=-\dfrac{24}{25} \quad \text { and } \quad \tan \left(\theta\right)=\dfrac{y}{x}=\dfrac{7}{-24}=-\dfrac{7}{24}\nonumber \]

Checkpoint \( \PageIndex{ 6} \)

1. If \(\cos \left(\theta\right)=\frac{5}{13}\) and \(-90^{\circ}<\theta<0^{\circ}\), find \(\sin \left(\theta\right)\) and \(\tan \left(\theta\right)\).
2. Find \(\sin \left(\theta\right)\) and \(\tan \left(\theta\right)\) by using an appropriate sketch.

Answers

\(\sin \left(\theta\right)=-\dfrac{12}{13}, \quad \tan \left(\theta\right)=-\dfrac{12}{5}\)

You might have noticed that this subsection is "Pythagorean Identities" (plural). Yet, we only named a single Pythagorean Identity (purposefully titled The Pythagorean Identity). We now introduce two additional Pythagorean Identities that will be used frequently throughout Trigonometry.\[ \begin{array}{rrclcr}
& \cos^2\left( \theta \right) + \sin^2\left( \theta \right) & = & 1 & \quad & (\text{The Pythagorean Identity}) \\
\\
\implies & \dfrac{\cos^2\left( \theta \right)}{\cos^2\left( \theta \right)} + \dfrac{\sin^2\left( \theta \right)}{\cos^2\left( \theta \right)} & = & \dfrac{1}{\cos^2\left( \theta \right)} & \quad & (\text{Dividing both sides by } \cos^2\left( \theta \right) ) \\
\\
\implies & 1 + \left(\dfrac{\sin\left( \theta \right)}{\cos\left( \theta \right)}\right)^2 & = & \left(\dfrac{1}{\cos\left( \theta \right)}\right)^2 & \quad & (\text{Cancelling like factors and Laws of Exponents} ) \\
\\
\implies & 1 + \left(\tan\left( \theta \right)\right)^2 & = & \left(\sec\left( \theta \right)\right)^2 & \quad & (\text{Ratio and Reciprocal Identities}) \\
\\
\implies & 1 + \tan^2\left( \theta \right) & = & \sec^2\left( \theta \right) & \quad & (\text{Laws of Exponents}) \\
\end{array} \nonumber \]A similar process shows\[ 1 + \cot^2\left( \theta \right) = \csc^2\left( \theta \right). \nonumber \]We formalize these statements in a summary theorem.

Theorem: Pythagorean Identities

For any angle \(\theta\) where the functions are defined,\[\begin{array}{rcl}
\cos^2 \left(\theta\right)+\sin^2 \left(\theta\right) & = & 1 \\
1 +\tan^2 \left(\theta\right) & = & \sec^2\left( \theta \right) \\
\cot^2 \left(\theta\right)+1 & = & \csc^2\left( \theta \right) \\
\end{array} \nonumber \]

Advice: Memorize These Identities

Each of the Pythagorean Identities are needed throughout the rest of Mathematics. While not as prevalent as the Pythagorean Theorem or the Quadratic Formula, the need to commit them to memory and their importance cannot be overstated.

---

Skills Refresher

Review the following skills you will need for this section.

Skills Refresher

For Problems 1 - 8, write the expression as a single fraction in simplest form.

1. \(\dfrac{1}{x} + \dfrac{1}{y}\)

2. \(1 - \dfrac{1}{x}\)

3. \(\dfrac{1}{x-1} + \dfrac{1}{x+1}\)

4. \(x - \dfrac{x}{x+1}\)

5. \(\dfrac{\frac{y}{x}-\frac{x}{y}}{\frac{y}{x} + 1}\)

6. \(\dfrac{1-\frac{x^2}{y^2}}{1+\frac{x^2}{y^2}}\)

7. \(\dfrac{\frac{2a}{x}}{1-\frac{a^2}{x^2}}\)

8. \(\dfrac{\frac{a}{x}+\frac{b}{y}}{1-\frac{ab}{xy}}\)

Answers

1. \(\dfrac{x+y}{xy}\)

2. \(\dfrac{x-1}{x}\)

3. \(\dfrac{2x}{x^2-1}\)

4. \(\dfrac{x^2}{x+1}\)

5. \(\dfrac{y-x}{y}\)

6. \(\dfrac{y^2-x^2}{y^2+x^2}\)

7. \(\dfrac{2ax}{x^2-a^2}\)

8. \(\dfrac{ay+bx}{xy-ab}\)

---

Homework

Vocabulary Check

1. A ___ equation is true only for certain variable values and false for others.

2. An equation that is true for all legitimate values of the variables is called a(n) ___.

3. The expressions on either side of the equal sign in an identity are called ___ because they have the same value for all values of the variable.

Concept Check

4. What is the difference between a conditional equation and an identity? Give an example of each.

5. What happens when you try to "solve" an identity?

6. Nhat claims that since \(\cos^2 \left(\theta\right) + \sin^2 \left(\theta\right) = 1\), we can take the square root of both sides to get the simpler form \(\cos \left(\theta\right) + \sin \left(\theta\right) = 1\). Is she correct? Why or why not?

7. If \(\frac{a}{b} = \frac{2}{5}\), is it necessarily true that \(a = 2\) and \(b = 5\)? Explain.

8. If \(\tan \left(\theta\right) = \frac{3}{11}\), is it true that \(\sin \left(\theta\right) = 3\) and \(\cos \left(\theta\right) = 11\)? Explain.

9. Explain how you would arrive at the identity\[ 1 + \cot^2\left( \theta \right) = \csc^2\left( \theta \right) \nonumber \]given that you know \( \cos^2\left( \theta \right) + \sin^2\left( \theta \right) = 1. \)

True or False? For Problems 10 - 14, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

10. The reciprocal of the secant is the cosecant.

11. For any angle \(\theta\),\[\cos ^2 \left(\theta\right)+\sin ^2 \left(\theta\right)=1.\nonumber \]

12. For any angle \(\theta\),\[\cos \left(\theta\right)+\sin \left(\theta\right)=1.\nonumber \]

13. For any angle \( \theta \),\[\tan \left(\theta\right)=\dfrac{\sin \left(\theta\right)}{\cos \left(\theta\right)}.\nonumber \]

14. To show that an equation is an identity, we just need to find one value of the unknown that makes the statement true.

Basic Skills

For Problems 15 - 22, decide which of the following equations are identities. Explain your reasoning.

15. \((\sqrt{a}+\sqrt{b})^2=a+b\)

16. \(\sqrt{a^2-b^2}=a-b\)

17. \(\dfrac{1}{a+b}=\dfrac{1}{a}+\dfrac{1}{b}\)

18. \(\dfrac{a+b}{a}=b\)

19. \(\tan (\alpha+\beta)=\dfrac{\sin (\alpha+\beta)}{\cos (\alpha+\beta)}\)

20. \(\dfrac{1}{\tan \theta}=\dfrac{\cos \theta}{\sin \theta}\)

21. \((1+\tan \theta)^2=1+\tan ^2 \theta\)

22. \(\sqrt{1-\sin ^2 \phi}=1-\sin \phi\)

For Problems 23 - 28, evaluate (without using a calculator).

23. \(3 \cos ^2 1.7^{\circ}+3 \sin ^2 1.7^{\circ}\)

24. \(4-\cos ^2 338^{\circ}-\sin ^2 338^{\circ}\)

25. \(\left(\cos ^2 20^{\circ}+\sin ^2 20^{\circ}\right)^4\)

26. \(\dfrac{18}{\cos ^2 17^{\circ}+\sin ^2 17^{\circ}}\)

27. \(\dfrac{6}{\cos ^2 53^{\circ}}-6 \tan ^2 53^{\circ}\)

28. \(\dfrac{1}{\sin ^2 102^{\circ}}-\dfrac{\cos ^2 102^{\circ}}{\sin ^2 102^{\circ}}\)

For Problems 29 - 42, find exact values for the other trigonometric functions of the given angle.

29. \(\cos A=\dfrac{12}{13} \quad\) and \(270^{\circ}<A<360^{\circ}\)

30. \(\sin B=\dfrac{-3}{5} \quad\) and \(180^{\circ}<B<270^{\circ}\)

31. \(\sin \phi=\dfrac{1}{7} \quad\) and \(90^{\circ}<\phi<180^{\circ}\)

32. \(\cos t=\dfrac{-2}{3} \quad\) and \(180^{\circ}<t<270^{\circ}\)

33. \(\tan \theta=-\dfrac{1}{2} \quad\) and \(270^{\circ}<\theta<360^{\circ}\)

34. \(\tan \theta=2\) and \(180^{\circ}<\theta<270^{\circ}\)

35. \(\tan \theta=\dfrac{3}{4} \quad\) and \(180^{\circ}<\theta<270^{\circ}\)

36. \(\tan \theta=-3\) and \(90^{\circ}<\theta<180^{\circ}\)

37. \(2 \cos A+9=8\) and \(90^{\circ}<A<180^{\circ}\)

38. \(25 \sin B+8=-12\) and \(180^{\circ}<B<270^{\circ}\)

39. \(8 \tan \beta+5=-11\) and \(90^{\circ}<\beta<180^{\circ}\)

40. \(6(\tan \beta-4)=-24\) and \(90^{\circ}<\beta<270^{\circ}\)

41. \(\tan ^2 C-\frac{1}{4}=0 \quad\) and \(0^{\circ}<C<180^{\circ}\)

42. \(4 \cos ^2 A-\cos A=0\) and \(0^{\circ}<A<180^{\circ}\)

Synthesis Questions

43. Proving the Pythagorean Identity. Prove the Pythagorean Identity \(\cos ^2 \theta+\sin ^2 \theta=1\) by carrying out the following steps. Sketch an angle \(\theta\) in standard position, and label a point \((x, y)\) on the terminal side, at a distance \(r\) from the vertex.

    1. Begin with the equation \(\sqrt{x^2+y^2}=r\), and square both sides.

    2. Divide both sides of your equation from part (a) by \(r^2\).

    3. Write the left side of the equation as the sum of the squares of two fractions.

    4. Substitute the appropriate trigonometric ratio for each fraction.

44. Proving the Ratio Identity. Prove the Ratio Identity \(\tan \theta=\frac{\sin \theta}{\cos \theta}\) by carrying out the following steps. Sketch an angle \(\theta\) in standard position, and label a point \((x, y)\) on the terminal side, at a distance \(r\) from the vertex.

    1. Write \(\sin \theta\) in terms of \(y\) and \(r\), and solve for \(y\).

    2. Write \(\cos \theta\) in terms of \(x\) and \(r\), and solve for \(x\).

    3. Write \(\tan \theta\) in terms of \(x\) and \(y\), then substitute your results from parts (a) and (b).

    4. Simplify your fraction in part (c).