7.3: Solving Trigonometric Equations - Algebraic Techniques

Suggested Prerequisite Topics

This section is designed assuming you understand the following topics from Algebra.

• Equations versus Expressions
• Factoring to solve quadratic equations.
• Using the Quadratic Formula to solve quadratic equations.

Learning Objectives

• Solve a simple trigonometric equation.
• Use techniques from algebra to solve a trigonometric equation.

The "Non-Uniqueness" of Solutions to Trigonometric Equations

Throughout Algebra, you constantly looked for "the" solution to an equation. For example, you might have been asked to solve\[ 3x-\dfrac{1}{2} = 10 \nonumber \]or\[ 2e^{2x-1} = 5 \nonumber \]or\[ \sqrt{5x - 1} = 3. \nonumber \]In each of these cases, the equation has a single solution; however, this was not the extent of your "equation solving" in Algebra. You also solved equations like\[ x^2 + 5x + 6 = 0 \nonumber \]and\[ \log_2\left( 5x^2-1 \right) = 2. \nonumber \]These last two equations each have two solutions. We now explore equations that often have an infinite number of solutions.

Trigonometric equations are equations whose terms are combinations of constants and trigonometric functions. For example,\[ 2\sec\left( x \right) - 1 = 0, \quad \sin^2\left( x \right) = 1, \quad \text{and} \quad 2\cos^2\left( x \right) = \sin\left( x \right) + 1 \nonumber \]are all trigonometric equations.

Before we discuss how to solve trigonometric equations, it's best to recall the graphical meaning of solutions of equations.

In Algebra, when you were asked to solve an equation like \( 2e^{2x-1} = 5 \), you learned all the mathematical manipulations - divide by \( 5 \), take the natural logarithm of both sides, add \( 1 \), then divide by \( 2 \). This results in the solution \( x = \frac{1}{2} \ln\left( \frac{5}{2} \right) + \frac{1}{2} \); however, before you learned how to procedurally work to an answer to such an equation, you learned a way to interpret this solution graphically.

When asked to solve an equation, one interpretation is that you are being asked to find the \( x \)-values for which the graph of the left side of the equation meets the graph of the right side. For example, when asked to solve \( 2e^{2x - 1} = 5 \), we could view the graphs of \( y = 2e^{2x - 1} \) and \( y = 5 \) to visualize the solution.

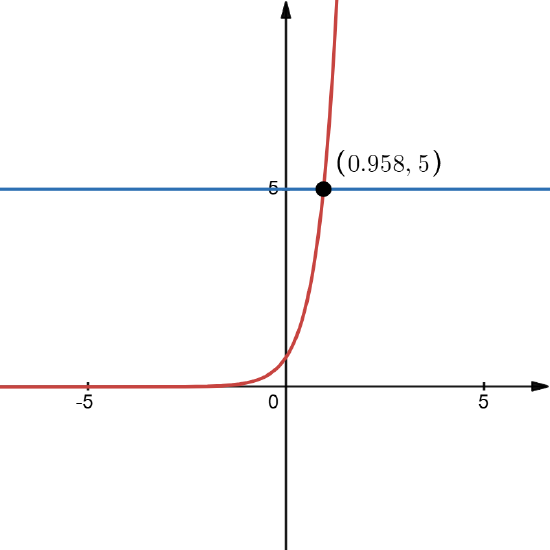
Figure \( \PageIndex{ 1 } \): The graphs of \( y = 2e^{2x-1}\) (red) and \( y = 5 \) (blue)

We can see in Figure \( \PageIndex{ 1 } \) that these graphs meet at \( 0.958 \approx \frac{1}{2} \ln\left( \frac{5}{2} \right) + \frac{1}{2} \).

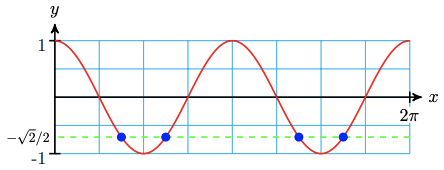
Although not the best way (or even a good way) to solve an equation, the visual we get from the example above justifies why trigonometric equations often have infinite solutions. For example, Figure \( \PageIndex{ 2 } \) illustrates that \(\sin (x)=0.5\) has five solutions on the interval \( \left[ -\frac{5\pi}{2}, \frac{5\pi}{2} \right] \). These solutions correspond to the points on the unit circle where \(y=0.5\). Since the sine function oscillates in both directions forever, we can easily imagine that the sine wave intersects the line \( y = 0.5 \) an infinite number of times.

Figure \( \PageIndex{ 2 } \): Using the sine curve to visualize solutions to \( \sin\left( x \right) = 0.5\)

Despite knowing there are an infinite number of solutions to \( \sin\left( x \right) = 0.5 \), we know from our recent discussions of the inverse trigonometric functions that \( x = \sin^{-1}\left( 0.5 \right) \) will only give us one of these solutions. Therefore, we must create a method to obtain all solutions to a given trigonometric equation.

Solving Basic Trigonometric Equations

The keys to finding all solutions to a trigonometric equation can be summarized in two fundamental concepts from Trigonometry: quadrants and reference angles. We will begin with an example to illustrate our thought process.

Example \( \PageIndex{ 1 } \)

Find all degree solutions to the equation\[\sin\left(\theta\right) = -0.6428,\nonumber \]and state the solutions occurring on the interval \( \left[ 0^{ \circ }, 360^{ \circ } \right] \). Round your answers to the nearest tenth of a degree.

Solution

Since \( -0.6428 \) is not a special ratio, we will need to use technology to help us find the solution; however, technology should be reserved for the last step in any mathematical procedure.
Quadrants: Since \( \sin\left( \theta \right) \) is negative, we know that \( \theta \) is either in \( \mathrm{QIII} \) or \( \mathrm{QIV} \).
Reference Angle: To find the reference angle, we compute\[ \sin^{-1}\left( \left| -0.6428 \right| \right) = \sin^{-1}\left( 0.6428 \right) \approx 40.0^{ \circ }. \nonumber \]
So we have a reference angle, \( \hat{\theta} \approx 40.0^{ \circ } \), and two quadrants, \( \mathrm{QIII} \) and \( \mathrm{QIV} \).
Solutions Associated with Quadrant III: The solution in \( \mathrm{QIII} \) having reference angle \( \hat{\theta} \approx 40.0^{ \circ } \) is\[ \theta = 180^{ \circ } + \hat{\theta} \approx 220.0^{ \circ }. \nonumber \]Since \( \sin\left( \theta \right) = \sin\left( \theta + 360^{ \circ }k \right) \) (where \( k \in \mathbb{Z} \)), any angle coterminal to \( 220.0^{ \circ } \) will also lead to a solution of our equation. Thus, the general solution associated with Quadrant III is\[ \theta \approx 220.0^{ \circ } + 360^{ \circ }k, \quad \text{where }k \in \mathbb{Z}. \nonumber \]
Solutions Associated with Quadrant IV: Taking a lesson from the previous paragraph, the solution in \( \mathrm{QIV} \) having reference angle \( \hat{\theta} \approx 40.0^{ \circ } \) is\[ \theta = 360^{ \circ } - \hat{\theta} + 360^{ \circ }k \approx 320.0^{ \circ } + 360^{ \circ }k, \quad \text{where }k \in \mathbb{Z}. \nonumber \]Now that we have all solutions, let's restrict them to only the solutions occurring on the interval \( \left[ 0^{ \circ },360^{ \circ } \right] \). To do this, we consider both sets of infinite solutions,\[ \begin{array}{rcl}
\theta & \approx & 220.0^{ \circ } + 360^{ \circ }k \\
\theta & \approx & 320.0^{ \circ } + 360^{ \circ }k, \\
\end{array} \nonumber \]and we let \( k = 0 \) (any other value of \( k \) will result in angles outside of the requested interval). Hence, the solutions on \( \left[ 0^{ \circ },360^{ \circ } \right] \) are approximately \( 220.0^{ \circ } \) and \( 320.0^{ \circ } \).

A few notes about Example \( \PageIndex{ 1 } \) are in order. First, our equation had solutions derived from two different quadrants. This should not be a surprise when you consider Figure \( \PageIndex{ 2 } \). The sine curve should attain a \( y \)-value of \( -0.6428 \) twice through any single cycle.

Second, since the given ratio, \( -0.6428 \), was not a special ratio, we had to grab a calculator to get an approximation of the reference angle by way of the arcsine. Moreover, we had to change our calculator to degree mode. You must remain aware of the angular measurement system in which you are being asked to work. You will frequently switch between degree and radian mode when solving trigonometric equations.

Third, we were told to round to the nearest tenth of a degree. If you are using online homework and need to answer with an approximation, pay attention to the level of rounding they request. If they don't state it explicitly, assume four decimal places (as this works well for most online homework systems).

Checkpoint \( \PageIndex{ 1 } \)

Solve the equation \(\sin\left(\theta\right)=-0.4\) for angles between \(0^{\circ}\) and \(360^{\circ}\). Round your answers to the nearest tenth of a degree.

Answer

\(203.6^{\circ}, 336.4^{\circ}\)

Example \(\PageIndex{2}\)

Find all solutions to the given equation, then state the solutions occurring on the interval \( \left[ 0,2\pi \right] \). Round your answers to the nearest tenth.

1. \( \sin\left( x \right) = \frac{1}{2} \)
2. \( \cos\left( x \right) = -0.6 \)
3. \( \tan\left( x \right) = -\sqrt{3} \)
4. \( \sec\left( x \right) = 3.7 \)

Solutions

1. Since \( \frac{1}{2} \) is a special ratio for the sine function, we do not bother (and should not bother) grabbing a calculator.
   Quadrants: Since \( \sin\left( x \right) = \frac{1}{2} \) is positive, we know that \( x \) is either in \( \mathrm{QI} \) or \( \mathrm{QII} \).
   Reference Angle: From our special triangles, we know that \( \hat{x} = \frac{\pi}{6} \).
   Solutions Associated with Quadrant I: The angle in Quadrant I with reference angle \( \frac{\pi}{6} \) is \( x = \frac{\pi}{6} \). Any angle coterminal with this will also be a solution to the given equation, so our set of solutions associated with Quadrant I is\[ x = \dfrac{\pi}{6} + 2 \pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]
   Solutions Associated with Quadrant II: The angle in Quadrant II with reference angle \( \frac{\pi}{6} \) is \( \frac{5\pi}{6} \). Thus,\[ x = \dfrac{5\pi}{6} + 2\pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]Finally, the solutions in the interval \( \left[ 0,2\pi \right] \) are \( x=\frac{\pi}{6} \) and \( x = \frac{5\pi}{6} \).
2. \( -0.6 \) is not a special ratio for cosine, so we will eventually need to reach for technology to solve this equation.
   Quadrants: We are given a negative cosine function, and we know this can only occur if the argument of the cosine terminates in either \( \mathrm{QII} \) or \( \mathrm{QIII} \).
   Reference Angle: To find the reference angle associated with the equation \( \cos\left( x \right) = -0.6 \), we approximate \( \cos^{-1}\left( \left| -0.4 \right| \right) = \cos^{-1}\left( 0.4 \right) \). It's important to note that we are looking for radian solutions to this equation, so we need to switch our calculator into radian mode.\[ \hat{x} = \cos^{-1}\left( 0.4 \right) \approx 1.159279481 \nonumber \]Notice that I wrote down all of the digits to the approximation the calculator returned. This is because we should save our rounding until the very end of the problem. We want to work with as many digits as possible but display a solution rounded to the nearest tenth to the reader.
   Solutions Associated with Quadrant II: The angle in Quadrant II having reference angle \( \hat{x} \) is \( \pi - \hat{x} \). Again, we list all coterminal angles as well.\[ x = \pi - \hat{x} + 2\pi k \approx 2.0 + 2 \pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]
   Solutions Associated with Quadrant III: The angle in Quadrant III having reference angle \( \hat{x} \) is \( \pi + \hat{x} \). Therefore,\[ x = \pi + \hat{x} + 2 \pi k \approx 4.3 + 2\pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]The solutions restricted to the interval \( \left[ 0,2\pi \right] \) are \( x \approx 2.0 \) and \( x \approx 4.3 \).
3. \( \frac{\sqrt{3}}{1} \) is definitely a special ratio for the tangent function, so we will abstain from calculator usage here.
   Quadrants: The given tangent function is negative, so we know the argument of the function terminates in either \( \mathrm{QII} \) or \( \mathrm{QIV} \).
   Reference Angle: From our special triangles, \( \hat{x} = \frac{\pi}{3} \).
   Solutions Associated with Quadrant II: The angle in Quadrant II having reference angle \( \hat{x} \) is \( \pi - \hat{x} \). Therefore,\[ x = \pi - \hat{x} + 2\pi k = \pi - \dfrac{\pi}{3} + 2 \pi k = \dfrac{2\pi}{3} + 2 \pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]
   Solutions Associated with Quadrant IV: The angle in Quadrant IV having reference angle \( \hat{x} \) is \( 2\pi - \hat{x} \). Therefore,\[ x = 2\pi - \hat{x} + 2 \pi k = 2 \pi - \dfrac{\pi}{3} + 2\pi k = \dfrac{5\pi}{3} + 2 \pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]The solutions restricted to the interval \( \left[ 0,2\pi \right] \) are \( x = \frac{2\pi}{3} \) and \( x = \frac{5\pi}{3} \).
4. \( 3.7 \) is not a special ratio for the secant, so we know we will need a calculator at some point.
   Quadrants: The given secant function is positive. Therefore, the argument terminates in either \( \mathrm{QI} \) or \( \mathrm{QIV} \).
   Reference Angle: Since our calculator doesn't have an inverse secant button, we rewrite \( \sec\left( x \right) = 3.7 \) using the Reciprocal Identities as\[ \cos\left( x \right) = \dfrac{1}{3.7}. \nonumber \]Therefore,\[ \hat{x} = \cos^{-1}\left( \left| \dfrac{1}{3.7} \right| \right) = \cos^{-1}\left( \dfrac{1}{3.7} \right) \approx 1.297122589. \nonumber \]
   Solutions Associated with Quadrant I: The angle in Quadrant I having reference angle \( \hat{x} \) is \( \hat{x} \). Thus,\[ x = \hat{x} + 2\pi k \approx 1.3 + 2 \pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]
   Solutions Associated with Quadrant IV: The angle in Quadrant IV having reference angle \( \hat{x} \) is \( 2\pi - \hat{x} \). Therefore,\[ x = 2\pi - \hat{x} + 2 \pi k \approx 5.0 + 2\pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]The solutions restricted to the interval \( \left[ 0,2\pi \right] \) are \( x \approx 1.3 \) and \( x \approx 5.0 \).

Note: Combining Solutions for the Tangent

We found the set of all solutions to Example \( \PageIndex{ 2c } \) to be\[ x = \dfrac{2\pi}{3} + 2\pi k \nonumber \]and\[ x = \dfrac{5 \pi}{3} + 2 \pi k. \nonumber \]However, the tangent and cotangent are special functions in the world of Trigonometry in that their natural periods are \( \pi \). That is, when finding their solutions, we can add \( \pi \) instead of \( 2\pi \).

For example, when solving \( \tan\left( x \right) = -\sqrt{3} \), we could have written our solution associated with Quadrant II as\[ x = \frac{2\pi}{3} + \pi k, \, \text{where} \, k \in \mathbb{Z}. \nonumber \]In doing so, we capture all of the Quadrant IV solutions as well because, when \( k = 1 \), \( x = \frac{2\pi}{3} + \pi = \frac{5 \pi}{3} \). This is precisely our Quadrant IV solution!

Thus, from this point forward, when solving trigonometric equations involving the tangent and cotangent functions, we will use this strategy to "combine" our solutions into a single statement.

Checkpoint \(\PageIndex{2}\)

Find exact solutions to the given equation, and then state the solutions occurring on the interval \( \left[ 0,2\pi \right] \).\[ \cos\left( x \right) = -\dfrac{1}{\sqrt{2}} \nonumber \]

Answer

\[ \begin{array}{rrcl}
\text{Solutions associated with QII}: & x & = & \dfrac{3\pi}{4} + 2\pi k, \, \text{where} \, k \in  \mathbb{Z} \\
\\
\text{Solutions associated with QIII}: & x & = & \dfrac{5\pi}{4} + 2 \pi k \, \text{where} \, k \in \mathbb{Z} \\ 
\end{array}\nonumber  \]On \( \left[ 0,2\pi \right] \), the solutions are \( x = \frac{3\pi}{4} \) and \( x = \frac{5\pi}{4} \).

Solving Trigonometric Equations Requiring Algebraic Techniques

The first Ferris wheel was built for the Chicago World’s Fair in 1893. It had a diameter of 250 feet and could carry 2160 people in 36 carriages. From the top of the wheel, passengers could see into four states. After loading all the passengers, the wheel made one revolution in nine minutes.

If you are in the bottom carriage of the Ferris wheel at the start of its revolution, your height after \(t\) seconds is given by\[h=f(t)=139-125 \cos \left(\dfrac{2 t}{3}\right).\nonumber \]For how long are you more than 240 feet above the ground?

Figure \( \PageIndex{ 3 } \) shows a graph of the height function and a horizontal line at \(h = 240\).

Figure \( \PageIndex{ 3 } \)

The graph shows that \(h=240\) at approximately 215 seconds and 325 seconds into the ride. Your height is more than 240 feet between those two times, or for about 110 seconds. To find a more precise solution, we can use algebraic methods. As an example, we’ll solve the slightly simpler equation\[139-125 \cos \left(\theta\right)=240.\nonumber \]We'll look for all solutions for \(\theta\) between \(0^{\circ}\) and \(360^{\circ}\). We begin by isolating the trigonometric ratio on one side of the equation.\[ \begin{array}{rrclcl}
& 139 - 125 \cos \left(\theta\right) & = & 240 & \quad & \\
\implies & -125 \cos \left(\theta\right) & = & 101 & \quad & \left(\text{subtract }139 \text{ from both sides} \right) \\
\implies & \cos \left(\theta\right) & = & -0.808 & \quad & \left( \text{divide both sides by }-125 \right) \\
\end{array} \nonumber \]We have solved equations like this one before: we use the inverse cosine to solve for \(\theta\). Remember that there are two angles between \(0^{\circ}\) and \(360^{\circ}\) that have a cosine of \(-0.808\), one in the second quadrant and one in the third quadrant. The reference angle is\[\hat{\theta} =\cos ^{-1}(|-0.808|)= \cos^{-1}(0.808) \approx 36.09901626^{\circ}.\nonumber \]Thus, the solution (rounded to the nearest tenth of a degree) in the second quadrant is\[ \theta = 180^{ \circ } - \hat{\theta} \approx 143.9^{ \circ } \nonumber \]and the solution in the third quadrant is\[ \theta = 180^{ \circ } + \hat{\theta} \approx 216.1^{ \circ }. \nonumber \]It's important to note that we have not discussed how to solve the original equation, \( 240 =139-125 \cos \left(\dfrac{2 t}{3}\right) \). Instead, we considered the slightly simpler version, \( 240=139-125 \cos \left(\theta\right) \). We will explore the original version a little bit later in this section.

In general, our old techniques of solving algebraic equations for an unknown still hold when solving trigonometric equations.

Example \( \PageIndex{ 3 } \)

Solve the equation \(4 \csc\left(\theta\right)-1=7\) for \(0^{\circ} \leq \theta \leq 360^{\circ}\).

Solution

We begin by isolating the trigonometric ratio.\[\begin{array}{rrclcl}
& 4 \csc\left(\theta\right)-1 & = & 7 & \quad & \\
\\
\implies & 4 \csc\left(\theta\right) & = & 8 & \quad & \left(\text{add }1\text{ to both sides}\right) \\
\\
\implies & \csc\left( \theta\right) & = & 2 & \quad & \left( \text{divide both sides by }4 \right) \\
\\
\implies & \sin\left( \theta\right) & = & \dfrac{1}{2} & \quad & \left( \text{Reciprocal Identity} \right) \\
\end{array}\nonumber \]
Quadrants: Sine is positive in \( \mathrm{QI} \) and \( \mathrm{QII} \).
Reference Angle: \(\frac{1}{2}\) is a special ratio for the sine function. Using our knowledge of the special triangles, we get the reference angle \(\hat{\theta}=30^{\circ}\).
Now that we know the angles terminate in \( \mathrm{QI} \) and \( \mathrm{QII} \) with reference angle \( \hat{\theta} = 30^{ \circ } \), we can confidently state the solutions are \( \theta = 30^{ \circ } \) and \(\theta=150^{\circ}\).

Checkpoint \( \PageIndex{ 3 } \)

Solve the equation \(5 \tan \left(\theta\right)+7=2\) for \(0 \leq \theta \leq 2\pi\).

Answer

\(\theta=\frac{3\pi}{4}\) and \(\theta=\frac{7\pi}{4}\)

Example \( \PageIndex{ 3 } \) and Checkpoint \( \PageIndex{ 3 } \) illustrate an implied angle measure. That is, in Example \( \PageIndex{ 3 } \), the statement, "for \(0^{\circ} \leq \theta \leq 360^{\circ}\)" implies our answer should be in degrees. Likewise, the statement, "for \(0 \leq \theta \leq 2\pi\)," in Checkpoint \( \PageIndex{ 3 } \), implies our answer should be in radians.

Example \( \PageIndex{ 4 } \)

Solve the equation \(3 \tan \left(\beta\right)+1=-8\) for \(0 \leq \beta \leq 2\pi\). Round your solutions to three decimal places.

Solution

First, we isolate the trigonometric ratio.\[\begin{array}{rrclcl}
& 3\tan\left( \beta\right) + 1 & = & -8 & \quad & \\
\implies & 3\tan \left(\beta\right) & = & -9 & \quad & \left( \text{subtract }1\text{ from both sides} \right) \\
\implies & \tan \left(\beta\right) & = & -3 & \quad & \left( \text{divide both sides by }3 \right) \\
\end{array}\nonumber \]There are two angles with tangent -3, one in the second quadrant and one in the fourth quadrant. The reference angle is \( \hat{\beta} = \tan^{-1}\left( 3 \right) \approx 1.249045772 \). Thus, we get the following:\[ \begin{array}{rrcl}
 \text{Solution Associated with QII}: & \beta & = & \pi - \hat{\beta} \approx 1.893 \\
\text{Solution Associated with QIV}: & \beta & = & 2\pi - \hat{\beta} \approx 5.034 \\
\end{array} \nonumber \]

It should not be surprising in Example \( \PageIndex{ 4 } \) that the solutions are \(\pi\) radians apart. As we mentioned previously, the solutions of an equation \(\tan \left(\theta\right)=k\) always differ by \( \pi \) radians (or \(180^{\circ}\)). Once we have found one solution, we can add \(\pi\) to find the other solution between \(0\) and \(2\pi\).

Checkpoint \( \PageIndex{ 4 } \)

Solve the equation \(3 \sec \left(C\right)-6=-2\), for \(0^{\circ} \leq C \leq 360^{\circ}\). Round your solutions to three decimal places.

Answer

\(C=41.410^{\circ}\) or \(C=318.590^{\circ}\)

Example \( \PageIndex{ 5 } \)

Solve \(\dfrac{\sin \left(\beta\right)}{5}-3=1 \) for \(0 \leq \beta \leq 2\pi\)

Solution

We begin by isolating \(\sin \left(\beta\right)\).\[ \begin{array}{rrclcl}
& \dfrac{\sin \left(\beta\right)}{5}-3 & = & 1 & \quad & \\
\\
\implies & \dfrac{\sin \left(\beta\right)}{5} & = & 4 & \quad & \left(\text{add }3\text{ to both sides} \right)\\
\\
\implies & \sin\left(\beta\right) & = & 20 & \quad & \left( \text{multiply both sides by }5 \right) \\
\end{array} \nonumber \]Because \(\sin\left(\beta\right)\) is never greater than 1, there is no angle \(\beta\) whose sine is 20. The equation has no solution.

Checkpoint \( \PageIndex{ 5 } \)

Solve \(2\sec \left(\theta\right)+5=-4\) for \(0^{\circ} \leq \theta \leq 360^{\circ}\).

Answer

No solution.

Example \( \PageIndex{ 5 } \) and Checkpoint \( \PageIndex{ 5 } \) show us that not all trigonometric equations have solutions. Just as you did in Algebra, you should pause after each step to check the result for realism. Forming this into a habit can save you time and frustration in the future.

The equations in Examples \( \PageIndex{ 3 } \) through \( \PageIndex{ 5 } \) are linear-in-form. That is, if you substitute a variable, say \( t \), for the trigonometric function, the equation would look like a linear equation in each case. The initial steps to solve the equation mimic those of a linear equation.

For example, the equation in Example \( \PageIndex{ 4 } \) could be written as \( 3t + 1 = -8 \). Solving for \( t \), we get \( t = -3 \); however, \( t \) was a substitution for \( \tan\left( \beta \right) \). Thus, \( \tan\left( \beta \right) = -3 \).

This tactic of simplifying the look of an equation using a substitution is beneficial as you move forward in Mathematics. While we will not use it in every example, Example \( \PageIndex{ 6 } \) (below) shows how it can be helpful.

Example \( \PageIndex{ 6 } \)

Solve \(4 \tan ^2 \left(\theta\right)+3=15\) for \(0 \leq \theta \leq 2\pi\).

Solution

We start with the substitution \( t = \tan\left( \theta \right) \) and solve \( 4t^2 + 3 = 15 \) for \( t \).\[ \begin{array}{rrclcl}
& 4 t^2  + 3 & = & 15 & \quad & \\
\implies & 4 t^2 & = & 12 & \quad & \left( \text{subtract}\,3\,\text{from both sides} \right) \\
\implies & t^2 & = & 3 & \quad & \left( \text{divide both sides by}\,4 \right) \\
\implies & t & = & \pm \sqrt{3} & \quad & \left( \text{Extraction of Roots} \right) \\
\end{array} \nonumber \]Resubstituting \( \tan\left( \theta \right) \) for \( t \), we get\[\tan \left(\theta\right)=\pm \sqrt{3}.\nonumber \]There are two angles between \(0\) and \(2\pi\) with tangent \(\sqrt{3}\) and two angles with tangent \(-\sqrt{3}\), making four solutions to this equation - one in each quadrant! Moreover, we know the reference angle such that \(\tan \left(\hat{\theta}\right)=\sqrt{3}\) is \( \hat{\theta} = \frac{\pi}{3} \).

Recall that tangent is the special function with period \( \pi \). Therefore, we only need to list the solutions associated with \( \mathrm{QI} \) and \( \mathrm{QII} \) and add integer multiples of \( \pi \) to get all other solutions.\[ \begin{array}{rrcl}
\text{Solutions associated with QI}: & \theta & = & \dfrac{\pi}{3} + \pi k, \, \text{where} \, k \in \mathbb{Z} \\
\\
\text{Solutions associated with QII}: & \theta & = & \pi - \hat{\theta} + \pi k = \pi - \dfrac{\pi}{3} + \pi k = \dfrac{2\pi}{3} + \pi k, \, \text{where} \, k \in \mathbb{Z} \\
\end{array} \nonumber \]To restrict this infinite set of solutions to those in the interval \( \left[ 0,2\pi \right] \), we let \( k = 0 \) and \( k = 1 \) to get\[ \theta = \dfrac{\pi}{3}, \dfrac{2\pi}{3}, \dfrac{4\pi}{3}, \, \text{and} \, \dfrac{5\pi}{3}. \nonumber \]

Checkpoint \( \PageIndex{ 6 } \)

Solve the equation \(2 \sin ^2 \left(\theta\right)=1\) for \(0^{\circ} \leq \theta \leq 360^{\circ}\).

Answer

\(\theta=45^{\circ}, \theta=135^{\circ}, \theta=225^{\circ}\), or \(\theta=315^{\circ}\)

Example \( \PageIndex{ 6 } \) is quadratic-in-form because, with the substitution \( t = \tan\left( \theta \right) \), it can be written as the quadratic equation \( 4t^2 + 3 = 15 \). From this point forward in Mathematics, you will be using your techniques from Algebra to solve trigonometric equations that are quadratic-in-form. If you are rusty with that material, I highly recommend reviewing it.

Example \( \PageIndex{ 7 } \)

Solve \(2 \cos ^2 \left(\theta\right)-\cos \left(\theta\right)-1=0 \quad\) for \(0 \leq \theta \leq 2\pi\).

Solution

Compare this equation to the algebraic equation \(2 t^2-t-1=0\). Our equation has the same algebraic form but with \(t\) replaced by \(\cos \left(\theta\right)\).

We can solve the algebraic equation by factoring \(2 t^2-t-1\) as \((2 t+1)(t-1)\), and we'll use the same strategy on the trigonometric equation.\[ \begin{array}{rrclcl}
& 2 \cos^2 \left(\theta\right)-\cos \left(\theta\right)-1 & = & 0 & \quad & \\
\implies & \left(2 \cos \left(\theta\right)+1\right)\left(\cos \left(\theta\right)-1\right) & = & 0 & \quad & \left( \text{factor} \right) \\
\end{array}\nonumber \]By the Zero Factor Property, this means\[ \begin{array}{rrclcccrcl}
& 2\cos\left( \theta \right) + 1 & = & 0 & \quad & \text{or} & \quad & \cos\left( \theta \right) - 1 & = & 0 \\
\\
\implies & \cos\left( \theta \right) & = & -\dfrac{1}{2} & \quad & \text{or} & \quad & \cos\left( \theta \right) & = & 1 \\
\end{array} \nonumber \]Now we solve each equation for \(\theta\).

For \( \cos\left( \theta \right) = -\frac{1}{2} \): We know cosine is negative in \( \mathrm{QII} \) and \( \mathrm{QIII} \) and that \( \hat{\theta} = \frac{\pi}{3} \). Thus,\[ \begin{array}{rrcl}
\text{Solutions associated with QII}: & \theta & = & \pi - \hat{\theta} + 2 \pi k = \pi - \dfrac{\pi}{3} + 2 \pi k = \dfrac{2\pi}{3} + 2 \pi k \\
\\
\text{Solutions associated with QIII}: & \theta & = & \pi + \hat{\theta} + 2 \pi k = \pi + \dfrac{\pi}{3} + 2\pi k = \dfrac{4\pi}{3} + 2 \pi k \\
 \end{array} \nonumber \]
For \( \cos\left( \theta \right) = 1 \): This will result in a quadrantal angle. Visualizing the graph of the cosine, we can (hopefully) see that the cosine attains a value of \( 1 \) at \( x = 0 \) and every integer multiple of \( 2\pi \) after that. That is,\[ \theta = 0 + 2\pi k = 2 \pi k. \nonumber \]
Combining all of these solution sets and restricting our answers to those between \( 0 \) and \( 2\pi \), we get\[ \theta = 0, \, \theta = \dfrac{2\pi}{3}, \, \theta = \dfrac{4\pi}{3}, \, \text{or} \, \theta = 2\pi. \nonumber \]

Checkpoint \( \PageIndex{ 7 } \)

Solve \(9 \sin ^2 \left(\theta\right)-3 \sin \left(\theta\right)=2\) for \(0^{\circ} \leq \theta \leq 360^{\circ}\). Round your answers to the nearest degree.

Answer

\(\theta=42^{\circ}, \theta=138^{\circ}, \theta=199^{\circ}\), or \(\theta=341^{\circ}\)

Solving Trigonometric Equations with Non-Standard Arguments

If \(n\) is an integer, what can we say about the solutions of the equation\[\sin \left(n x\right)=k?\nonumber \]For example, how many solutions are there for the equation \(\sin \left(2 x\right)=0.5\)? Truthfully, we already know there will be an infinite number of solutions; however, on the interval from \( 0 \) to \( 2\pi \), how many solutions will this equation have?

As was stated earlier in the text, the coefficient of \( x \) can be thought of as the number of oscillations over an interval of length equal to the natural period of the function. That is, \( \sin\left( 2x \right) \) goes through two full oscillations on any interval of length \( 2\pi \). Compare Figure \( \PageIndex{ 4 } \) (below) to Figure \( \PageIndex{ 2 } \).

Figure \( \PageIndex{ 4 } \): Visualizing solutions to \( \sin\left( 2x \right) = 0.5 \)

You can see there are twice as many solutions on the same interval as that of \( \sin\left( x \right) = 0.5 \). This visual helps us wrap our brains around the fact that the number of solutions to such equations over an interval like \( \left[ 0,2\pi \right] \) might be more (or less) than two.

Example \( \PageIndex{ 8 } \)

Find all solutions of \(\sin \left(2 x\right)=0.5\) between \(0\) and \(2 \pi\).

Solution

Treat the argument as if it were a single variable. The sine is positive, meaning the angle, \( 2x \), must terminate in \( \mathrm{QI} \) or \( \mathrm{QII} \). Additionally, we know that the reference angle is \( \widehat{2x} = \frac{\pi}{6} \). At this point, let's pause to make sure we understand what just happened. I am treating the argument of the sine, which is \( 2x \), as a single variable - sort of like calling it \( \theta \). Once I find a reference angle, I have found it for that single variable, which is \( 2x \). Like we traditionally do, we use the "hat" notation to denote the reference angle; however, in this case, the reference angle is for \( 2x \) - not \( x \). Therefore, our reference angle notation is \( \widehat{2x} \).

Continuing as usual,\[ \begin{array}{rrcl}
\text{Solutions associated with QI}: & 2x & = & \dfrac{\pi}{6} + 2 \pi k \\
\\
\text{Solutions associated with QII}: & 2x & = & \dfrac{5\pi}{6} + 2 \pi k \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). We finally arrive at the reason why I write "Solutions associated with" rather than "Solutions in." Our goal is to solve for \( x \). This requires us to divide both equations by \( 2 \) (including dividing the \( 2\pi k \)). Therefore, we get\[ \begin{array}{rrcl}
\text{Solutions associated with QI}: & x & = & \dfrac{\pi}{12} + \pi k \\
\\
\text{Solutions associated with QII}: & x & = & \dfrac{5\pi}{12} + \pi k \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). Do you notice that the "Solutions associated with QII" doesn't start with a Quadrant II angle? That's perfectly fine! The solution angles have been adjusted by the coefficient of \( x \) so they might not belong to the original quadrant they were derived from. This is why I use the words "associated with."

We now need to restrict our answers to the interval \( \left[ 0,2\pi \right] \). Allowing \( k = 0 \), we get \( x = \frac{\pi}{12} \) and \( x = \frac{5\pi}{12} \) - both of which are in the requested interval. Trying \( k = 1 \), we get \( x = \frac{13\pi}{12} \) and \( x = \frac{17\pi}{12} \). Again, both of these solutions are still within the requested interval. Trying \( k = 2 \), however, gives \( x = \frac{25\pi}{12} \) and \( x = \frac{29\pi}{12} \). Neither of these are in the requested interval. Thus, the solutions on \( \left[ 0,2\pi \right] \) are\[ x = \dfrac{\pi}{12}, \, x = \dfrac{5\pi}{12}, \, \dfrac{13\pi}{12}, \, \text{or} \, x = \dfrac{17\pi}{12}.\nonumber \]

Notice in Example \( \PageIndex{ 8 } \), that we had twice the number of solutions we would typically expect. Do you see why?

Checkpoint \( \PageIndex{ 8 } \)

1. Sketch a graph of \(y=\cos \left(2 x\right)\) for \(0 \leq \theta \leq 2 \pi\).
2. Find exact values for all solutions of \(\cos \left(2 x\right)=-\frac{1}{\sqrt{2}}\) between 0 and \(2 \pi\).

Answer

1. 
   
2. \(\dfrac{3 \pi}{8}, \dfrac{5 \pi}{8}, \dfrac{11 \pi}{8}, \dfrac{13 \pi}{8}\)

As we observed earlier, equations involving the tangent function are easier to solve because there is only one solution in each cycle of the graph. Once we have found one solution, we can find all the others by adding multiples of the period.

Example \( \PageIndex{ 9 } \)

Find all solutions of \(\tan \left(2 t\right)=-1\) between \(0\) and \(2 \pi\).

Solution

Again, treating the argument, \( 2t \), as a single variable, we know the tangent is negative in \( \mathrm{QII} \) and \( \mathrm{QIV} \); however, the tangent is that special case (along with the cotangent) where we can say the second solution is just \( \pi \) plus the first solution. So, we only need to concentrate on the solution in the second quadrant. The reference angle is \( \widehat{2t} = \frac{\pi}{4} \). This is all we need!\[ \begin{array}{rrcl}
\text{Solutions associated with QII}: & 2t & = & \dfrac{3\pi}{4} + \pi k \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). We then divide both sides of the equation by 2 to get\[ \begin{array}{rrcl}
\text{Solutions associated with QII}: & t & = & \dfrac{3\pi}{8} + \dfrac{\pi}{2} k \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). Just so you can see a different approach, let's build a table to get all the solutions between \( 0 \) and \( 2\pi \).\[ \begin{array}{|c|c|}
\hline
k & \dfrac{3\pi}{8} + \dfrac{\pi}{2}k \\
\hline
0 & \dfrac{3\pi}{8} \\
\\
1 & \dfrac{7\pi}{8} \\
\\
2 & \dfrac{11\pi}{8} \\
\\
3 & \dfrac{15\pi}{8} \\
\hline \end{array} \nonumber \]If we move to \( k=4 \), the solutions will be outside of the requested interval. Thus, our solutions are \(\frac{3 \pi}{8}, \frac{7 \pi}{8}, \frac{11 \pi}{8}\) and \(\frac{15 \pi}{8}\). The following figure gives a visual of these solutions.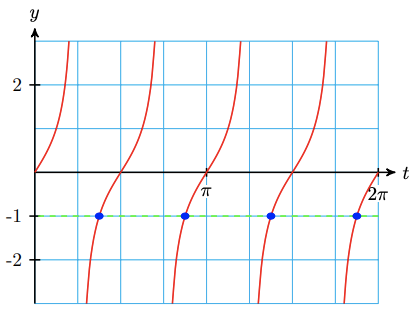

Checkpoint \( \PageIndex{ 9 } \)

Find all solutions of \(\tan \left(2 x\right)=\sqrt{3}\) between \(0\) and \(2 \pi\).

Answer

\(\dfrac{\pi}{6}, \dfrac{2 \pi}{3}, \dfrac{7 \pi}{6}, \dfrac{5 \pi}{3}\)

The tactics shown in Examples \( \PageIndex{ 8 } \) and \( \PageIndex{ 9 } \) work for more complicated equations.

Example \( \PageIndex{ 10 } \)

Solve \(\sin (2 x+1.5)=-0.3\) for \(0 \leq x \leq 2 \pi\). Round your answer to four decimal places.

Solution

Again, we treat the entire argument as a single variable. The sine is negative in \( \mathrm{QIII} \) and \( \mathrm{QIV} \). Since \( -0.3 \) is not a special ratio for the sine, we will have to use technology. The reference angle is given by\[ \widehat{2x+1.5} = \sin^{-1}\left( \left| -0.3 \right| \right) = \sin^{-1}\left( 0.3 \right) \approx 0.304692654. \nonumber \]Therefore,\[ \begin{array}{rrcl}
\text{Solutions associated with QIII}: & 2x + 1.5 & = & \pi + \widehat{2x+1.5} + 2 \pi k \\
\\
\text{Solutions associated with QIV}: & 2x + 1.5 & = & 2\pi - \widehat{2x + 1.5} + 2 \pi k \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). Despite having an approximation for the reference angle, \( \widehat{2x+1.5} \), I like to leave the equations in exact form (without decimal approximations) until I get to a final answer. Subtracting \( 1.5 \) from both sides of each equation and dividing by \( 2 \), we get the following:\[ \begin{array}{rrcl}
\text{Solutions associated with QIII}: & x & = & \dfrac{\pi}{2} + \dfrac{\widehat{2x+1.5}}{2} + \pi k - 0.75 \\
\\
\text{Solutions associated with QIV}: & x & = & \pi - \dfrac{\widehat{2x + 1.5}}{2} + \pi k - 0.75 \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). At this time, I will use technology to find an approximation for these solutions.\[ \begin{array}{rrcl}
\text{Solutions associated with QIII}: & x & = & 0.973142654 + \pi k \\
\\
\text{Solutions associated with QIV}: & x & = & 2.239246327 + \pi k \\
\end{array} \nonumber \]where \( k \in \mathbb{Z} \). Let's build a table like we did in Example \( \PageIndex{ 9 } \).\[ \begin{array}{|c|c|c|}
\hline
k & 0.973142654 + \pi k & 2.239246327 + \pi k \\
\hline
0 & 0.973142654 & 2.239246327 \\
\\
1 & 4.114735308 & 5.38083898 \\
\hline \end{array} \nonumber \]Going to \( k=2 \) gives solutions outside of the requested interval. Thus, the solutions on \( \left[ 0,2\pi \right] \) are 0.9731, 2.2392, 4.1147, and 5.3808.

Checkpoint \( \PageIndex{ 10 } \)

Solve \(4 \cos (3 x-0.5)=-3.2\) for \(0 \leq x \leq 2 \pi\).

Answer

1.00, 1.43, 3.09, 3.52, 5.19, 5.62

Applications

Trigonometric equations often arise in the study of periodic models.

Example \( \PageIndex{ 11 } \)

A piston is pumping vertically at a rate of 1000 cycles per second. The distance between its lowest and highest position is 16 centimeters.

1. Suppose the piston is at its midline position at \(t=0\) and moving downwards. Find a formula for the sinusoidal function \(h(t)\) that gives the piston's height.
2. Use the formula to find the first two times the piston is 14 centimeters above its lowest position.

Solutions

1. Because the piston starts at its midline and moves down, we will write \(h(y)\) as a sine function:\[h(t)=-A \sin (B t)+D.\nonumber \]The amplitude is \(A=\frac{16}{2}=8\), and the midline is \(D=8\). The period is \(\frac{1}{1000}\), so \(\frac{B}{1000}=2 \pi\), and \(B=2000 \pi\). Thus,\[h(t)=-8 \sin (2000 \pi t)+8.\nonumber \]The graph is shown below.
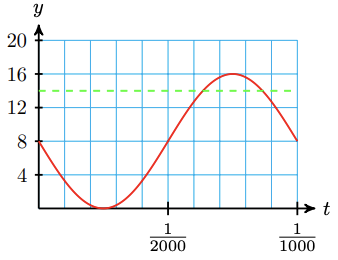
2. With \(h(t)=14\), we have\[\begin{array}{rrclcl}
   & -8 \sin (2000 \pi t)+8 & = & 14 & \quad & \\
   \\
   \implies & -8 \sin (2000 \pi t) & = & 6 & \quad & \left( \text{subtract}\,8\,\text{from both sides} \right) \\
   \\
   \implies & \sin (2000 \pi t) & = & -\dfrac{3}{4} & \quad & \left( \text{divide both sides by}\,-8 \right) \\
   \end{array} \nonumber \]Sine is negative in \( \mathrm{QIII} \) and \( \mathrm{QIV} \). Moreover, we can compute the reference angle as follows:\[\widehat{2000 \pi t} = \sin ^{-1}\left(\left|-\dfrac{3}{4}\right|\right) = \sin^{-1}\left( \dfrac{3}{4} \right) \approx 0.848062079.\nonumber \]We want the first two positive solutions to this equation.\[ \begin{array}{rrclcl}
   \text{Solutions associated with QIII}: & 2000 \pi t & = & \pi + \sin^{-1}\left( \dfrac{3}{4} \right) + 2 \pi k & \implies & t = \dfrac{1}{2000} + \dfrac{\sin^{-1}\left( \dfrac{3}{4} \right)}{2000 \pi} + \dfrac{1}{1000} k \\
   \\
   \text{Solutions associated with QIV}: & 2000 \pi t & = & 2\pi - \sin^{-1}\left( \dfrac{3}{4} \right) + 2 \pi k & \implies & t = \dfrac{1}{1000} - \dfrac{\sin^{-1}\left( \dfrac{3}{4} \right)}{2000 \pi} + \dfrac{1}{1000} k \\
   \end{array} \nonumber \]where \( k \in \mathbb{Z} \). Building a quick table, we get the following:\[ \begin{array}{|c|c|c|}
   \hline
   k & \dfrac{1}{2000} + \dfrac{\sin^{-1}\left( \dfrac{3}{4} \right)}{2000 \pi} + \dfrac{1}{1000} k & \dfrac{1}{1000} - \dfrac{\sin^{-1}\left( \dfrac{3}{4} \right)}{2000 \pi} + \dfrac{1}{1000} k \\
   \hline
   0 & 0.000634973 & 0.000865027 \\
   \\
   1 & 0.001634973 & 0.000965027 \\
   \\
   \vdots & \vdots & \vdots \\
   \hline \end{array} \nonumber \]From our table, we can see the first two times the piston is at a height of 14 centimeters are approximately \(t=0.000865\) and \(t=0.000635\) seconds.

Checkpoint \( \PageIndex{ 11 } \)

A lever on an oil well is pumping vertically at a rate of 10 cycles per minute. The distance between its lowest position at the ground and its highest position is 1.8 meters.

1. Suppose the lever is at its midline position at \(t=0\) and moving downwards. Find a formula for the sinusoidal function \(h(t)\) that gives the lever's height.
2. Find the first two times the lever is 1 meter above its lowest position.

Answer

1. \(h(t)=-0.9 \sin (20 \pi t)+0.9\)
2. 0.0518 minutes and 0.9823 minutes

---

Skills Refresher

Review the following skills you will need for this section.

Skills Refresher

For Problems 1 - 6, solve the equation.

1. \((2x - 6)^2 = 4\)

2. \(\sqrt{2x-6} = 4\)

3. \(\dfrac{1}{2x-6} = 4\)

4. \(|2x-6| = 4\)

5. \(\log 2x-6 = 4\)

6. \(2^{2x-6} = 4\)

For Problems 7 - 10, the ”solution” contains an error. Find the error, and supply a correct solution.

7.  \[\begin{array}{rrcl}
   & 3x^2-5x & = & 0 \\
   \\
   \implies & 3x^2 & = & 5x \\
   \\
   \implies & 3x & = & 5 \\
   \\
   \implies & x & = & \dfrac{5}{3} \\
   \end{array} \nonumber \]
8.  \[\begin{array}{rrcl}
   & 4x^2 - 5x & = & 12 \\
   \implies & x^2 & = & 3 \\
   \implies & x & = & \sqrt{3} \\
   \end{array} \nonumber \]
9.  \[\begin{array}{rrcl}
   & (2x+1)^2 & = & 4 \\
   \\
   \implies & 2x+1 & = & 2 \\
   \\
   \implies & 2x & = & 1 \\
   \\
   \implies & x & = & \dfrac{1}{2} \\
   \end{array} \nonumber \]
10.  \[\begin{array}{rrcl}
    & 2x^2-4x & = & 3 \\
    \\
    \implies & 2x(x-2) & = & 3 \\
    \\
    \implies & 2x=3 & \text{ or } & x-2=3 \\
    \\
    \implies & x = \dfrac{3}{2} & \text{ or } & x=5 \\
    \end{array}\nonumber \]

Answers

1. 2, 4

2. 11

3. \(\dfrac{25}{8}\)

4. 1, 5

5. 5003

6. 4

7. We can't divide by \(x\). \(x = 0, \dfrac{5}{3}\)

8. 3 has two square roots. \(x = \pm \sqrt{3}\)

9. 4 has two square roots. \(x = \dfrac{-3}{2},\dfrac{1}{2}\)

10. One side must be zero to use the zero-factor principle. No real solutions.

---

Homework

Concept Check

1. How many solutions between \(0^{\circ}\) and \(360^{\circ}\) does the equation \(\cos \left(\theta\right) = k\) have for each value of \(k\) between \(-1\) and \(0\)?

2. How many solutions between \(0^{\circ}\) and \(360^{\circ}\) does the equation \(\cos \left(\theta\right) = k\) have for each value of \(k\) greater than \(1\)?

3. How many solutions between \(0^{\circ}\) and \(360^{\circ}\) does the equation \(\sin^2 \left(\theta\right) = k\) have for each value of \(k\) between \(-1\) and \(0\)?

4. If \(x=0.68\) is one solution of the equation \(\cos \left(x\right)=c\), what is other? Illustrate on a unit circle.

5. If \(t=2.45\) is one solution of the equation \(\sin \left(t\right)=k\), what is the other? Illustrate on a unit circle.

6. If \(\theta=1.73\) is one solution of the equation \(\tan \left(\theta\right)=C\), what is the other?

7. Explain why the equation \(\cos \left(n x\right)=k, \quad 0 \lt k \lt 1\), has \(2 n\) solutions between \(0\) and \(2 \pi\).

8. How many solutions are there to the equation \(\cos \left(\theta\right)=0.4\)? How many solutions are there between \(0\) and \(2\pi\)?

9. Find all angles between \(0^{\circ}\) and \(360^{\circ}\) for which the statement is true.

   1. \(\cos \left(\theta\right) = -1\)

   2. \(\sin \left(\theta\right) = -1\)

   3. \(\tan \left(\theta\right) = -1\)

10.  

    1. Find two angles, \(0 \leq \theta \leq 360^{\circ}\), with \(\sin \left(\theta\right) = 0\).

    2. Find two angles, \(0 \leq \theta \leq 360^{\circ}\), with \(\cos \left(\theta\right) = 0\).

11.  

    1. Find two angles, \(0 \leq \theta \leq 360^{\circ}\), with \(\sin \left(\theta\right) = \cos \left(\theta\right)\).

    2. Find two angles, \(0 \leq \theta \leq 360^{\circ}\), with \(\sin \left(\theta\right) = -\cos \left(\theta\right)\).

Basic Skills

For Problems 12 - 15,
(a) Evaluate the expression at the given values of the variable.
(b) Give one solution to the equation.

12.  

    1. \(\sin\left(\theta\right)+\cos\left(\theta\right) ; \quad \theta=0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}\)

    2. \(\sin\left(\theta\right)+\cos\left(\theta\right)=\sqrt{2}\)

13.  

    1. \(\sin ^2 \left(\alpha\right)-\cos \left(\alpha\right) ; \quad \alpha = \frac{\pi}{4}, \frac{\pi}{2}, \frac{3\pi}{4}, \pi\)

    2. \(\sin ^2 \left(\alpha\right)-\cos \left(\alpha\right)=1\)

14.  

    1. \(\sin \left(\beta\right)+2 \cos ^2 \left(\beta\right) ; \quad \beta=210^{\circ}, 225^{\circ}, 240^{\circ}, 270^{\circ}\)

    2. \(\sin \left(\beta\right)+2 \cos ^2 \left(\beta\right)=-1\)

15.  

    1. \(3 \cos ^2 \left(\phi\right)-\sin ^2 \left(\phi \right); \quad \phi=\frac{3\pi}{2}, \frac{5\pi}{3}, \frac{7\pi}{4}, \frac{11\pi}{6}\)

    2. \(3 \cos ^2 \left(\phi\right)-\sin ^2 \left(\phi\right)=2\)

For Problems 16 - 44, find all degree solutions (in exact form) and then state the solutions for \(0^{\circ} \leq \theta \leq 360^{\circ}\).

16. \(7 \sin \left(\theta\right)+11=11\)

17. \(3=5-4 \cos \left(\theta\right)\)

18. \(3 \tan \left(\theta\right)=\sqrt{3}\)

19. \(8 \csc \left(\theta\right)+5=-11\)

20. \(9 \sec \left(\theta\right)+15=6\)

21. \(6 \cot \left(\theta\right)+21=15\)

22. \(0=\sqrt{2}+2 \sin \left(\theta\right)\)

23. \(\sqrt{3} \cos \left(\theta\right)=-\frac{3}{2}\)

24. \(\cos ^2 \left(\theta\right)-1=0\)

25. \(1-\sin ^2 \left(\theta\right)=0\)

26. \(3 \csc ^2 \left(\theta\right)-4=0\)

27. \(0=4-2 \sec ^2 \left(\theta\right)\)

28. \(1-\tan ^2 \left(\theta\right)=0\)

29. \(0=2 \cot ^2 \left(\theta\right)-6\)

30. \(2 \sin^2 \left(\theta\right)+\sin \left(\theta\right)-1=0\)

31. \(4 - \cos\left( \theta \right) = 4 \cos^2 \left(\theta\right)+3\cos \left(\theta\right)+5\)

32. \( 2\sin^2\left( \theta \right) - 11\sin\left( \theta \right) = -5 \)

33. \( 2 = \csc^2\left( \theta \right) - \csc\left( \theta \right)\)

34. \( \sec^2\left( \theta \right) + 3\sec\left( \theta \right) + 2 = 0\)

35. \(\sin \left(4 x\right)=-1\)

36. \(\cos \left(3 t\right)=0\)

37. \(5 \tan \left(2 q\right)=0\)

38. \(6 \sin \left(4 w\right)=-3 \sqrt{2}\)

39. \(4 \cos \left(3 \phi\right)=-2\)

40. \(2 \tan \left(2 \pi \beta\right)+5=3\)

41. \(160 \sin (\pi \phi-1)+10=90\)

42. \(2 \cos \left(3 t+\frac{\pi}{4}\right)=\sqrt{3}\)

43. \(2-\tan \left(2 x-\frac{\pi}{3}\right)=2\)

44. \(7 \csc \left(\frac{\phi}{2}+\frac{3 \pi}{4}\right)+3=-4\)

For Problems 45 - 79, find all radian solutions (in exact form) and then state the solutions for \( 0 \leq \theta \leq 2\pi \).

45. \(\sqrt{2} \sin \left(\theta\right)+9=8\)

46. \(\tan\left( x \right)-2\sin\left( x \right)\tan\left( x \right)=0\)

47. \(13=13-4 \cos \left(\theta\right)\)

48. \(4 \tan \left(\theta\right) - 2 = -6\)

49. \(8 \csc \left(\theta\right)+5=-3\)

50. \(2\cos^2\left( t \right)+\cos\left( t \right)=1\)

51. \(\sec\left( x \right)\sin\left( x \right)-2\sin\left( x \right)=0\)

52. \(-6 \sec \left(\theta\right)+4=-8\)

53. \(3 \cot \left(\theta\right)+\frac{2}{\sqrt{3}}=-\frac{1}{\sqrt{3}}\)

54. \(0=4\sqrt{2}+8 \sin \left(\theta\right)\)

55. \(\sqrt{3} \cos \left(\theta\right)=-\frac{3}{2}\)

56. \(\sin ^2 \left(\theta\right)-1=0\)

57. \(1-\cos ^2 \left(\theta\right)=0\)

58. \(4 \sec ^2 \left(\theta\right)-3=0\)

59. \(0=1.5-0.75 \csc ^2 \left(\theta\right)\)

60. \(1-\cot ^2 \left(\theta\right)=0\)

61. \(0=-6 + 18 \tan ^2 \left(\theta\right)\)

62. \(\tan^5\left( x \right)=\tan\left( x \right)\)

63. \(2 \sin^2 \left(\theta\right)+3\sin \left(\theta\right)=-1\)

64. \( 3 = 6 \cos^2 \left(\theta\right) -3\cos \left(\theta\right)\)

65. \(8\sin^2\left( x \right)+6\sin\left( x \right)+1=0\)

66. \(\tan^2\left( x \right)=-1+2\tan\left( -x \right)\)

67. \( 2\cos^2\left( \theta \right) +7\cos\left( \theta \right) + 3 = 0 \)

68. \( -2 = \csc^2\left( \theta \right) - 3\csc\left( \theta \right)\)

69. \( \sec^2\left( \theta \right) - 2 = - \sec\left( \theta \right) \)

70. \(\sqrt{3} \tan \left(2 \alpha\right)=3\)

71. \(2 \sin \left(2 \beta\right)=1\)

72. \(-6 \cos \left(2 \theta\right)=6\)

73. \(3 \tan \left(3 w\right)=\sqrt{3}\)

74. \(2 \tan \left(3 u\right)=-2\)

75. \(\frac{5}{7} \tan \left(\pi x\right)+11=11\)

76. \(8 \sin \left(2 \theta-\frac{\pi}{6}\right)=-4\)

77. \(6 \cos \left(3 \theta-\frac{\pi}{2}\right)=-3 \sqrt{2}\)

78. \(3 \tan \left(\frac{w}{2}+\frac{\pi}{4}\right)+4=1\)

79. \(50 \sec \left(\frac{t}{\pi}+6\right)-10=-110\)

For Problems 80 - 105, solve the equation for \(0^{\circ} \leq \theta \leq 360^{\circ}\). Round your answers to two decimal places.

80. \(4=6 \sin \left(\theta\right)\)

81. \(3=5 \cos \left(\theta\right)\)

82. \(\frac{1}{2} \tan \left(\theta\right)-1=-3\)

83. \(7 \csc \left(\theta\right)+2=-16\)

84. \(3 \sec \left(\theta\right)-2=5\)

85. \(2=5-\frac{1}{3} \cot \left(\theta\right)\)

86. \(6 \cos ^2 \left(\theta\right)=2\)

87. \(2-7 \sin ^2 \left(\phi\right)=1\)

88. \( -4\tan^2\left( \theta \right) + 5 = -4 \)

89. \( 8 - 2\sec^2\left( \theta \right) = -2 \)

90. \( 3 = 9 - 2 \csc^2\left( \theta \right) \)

91. \( 9\cot^2\left( \theta \right) - 9 = -5 \)

92. \(5 \sin ^2 \left(\theta\right)+\sin \left(\theta\right)=0\)

93. \(10 \cos ^2 \left(\theta\right)-7 \cos \left(\theta\right)+1=0\)

94. \(4 \tan ^2 \left(\theta\right)=\tan \left(\theta\right)\)

95. \(\cot ^2 \left(\theta\right)-2 \cot \left(\theta\right)=15\)

96. \(5 \sin \left(3 \theta\right)-3=-4\)

97. \(9 \cos \left(2 \theta\right)+1=6\)

98. \(8 \tan \left(4 t\right)+1=-11\)

99. \(6 \csc \left(2 r\right)+2=13\)

100. \(120 \sin \left(\frac{\pi}{3}(t-0.2)\right)+21=-3\)

101. \(16 \cos (3 t-1)+4=-8\)

102. \(23-24 \tan (\pi x+2)=17\)

103. \(3 \csc \left(3 w-\frac{\pi}{3}\right)+1=6\)

104. \(12 \sec \left(\frac{\pi}{2}(t+0.3)\right)-7=9\)

105. \(8 \cot \left(4 t-\frac{\pi}{3}\right)-24=1\)

For Problems 106 - 131, solve the equation for \(0 \leq \theta \leq 2\pi\). Round your answers to two decimal places.

106. \( 5\sin\left( \theta \right) - 4 = -6 \)

107. \( -4 + 3 \cos\left( \theta \right) = -2\)

108. \( -2\tan\left( \theta \right) + 5 = 6 \)

109. \( -4 = 5 - \csc\left( \theta \right) \)

110. \( 3\sec\left( \theta \right) - 2 = -10 \)

111. \( \frac{1}{3}\cot\left( \theta \right) + 1 = -2 \)

112. \(5 \sin ^2 \left(\theta\right)=2\)

113. \(3-6 \cos ^2 \left(\phi\right)=-1\)

114. \( 4-4\tan^2\left( \theta \right) = -5 \)

115. \( 4 - \sec^2\left( \theta \right) = -1 \)

116. \( -1 + 2 \csc^2\left( \theta \right) = 5\)

117. \( \frac{9}{2}\cot^2\left( \theta \right) - 1 = 1 \)

118. \(\sin ^2 \left(\theta\right)+8 \sin \left(\theta\right)+7=0\)

119. \(\cos ^2 \left(\theta\right)-4 \cos \left(\theta\right)+3=0\)

120. \(\tan ^2 \left(\theta\right)-5 \tan \left(\theta\right)+6=0\)

121. \(6 \cot ^2 \left(\theta\right)-\cot \left(\theta\right)-1=0\)

122. \(150 \sin \left(3 s\right)=27\)

123. \(7 \cos \left(2 t\right)-3=2\)

124. \(3=3 \tan \left(4 x\right)+4\)

125. \(2-8 \sec \left(3 t\right)=-10\)

126. \(9 \sin \left(\frac{\pi}{2}(t-1)\right)+5=-1\)

127. \(3-5 \cos (2 \phi-1)=6\)

128. \(14 \tan (\pi \beta-4)+31=10\)

129. \(0.3 \csc \left(\frac{\pi}{2}(\alpha+0.1)\right)+0.4=1.9\)

130. \(2 \sec \left(\frac{\pi}{4}\left(t+\frac{1}{4}\right)\right)+3=-7\)

131. \(6 \cot \left(\frac{\pi}{3}(\theta-1)\right)+4=5\)

Proofs

132. What is the angle in the first quadrant with reference angle \( \theta \)? What is the angle in the third quadrant with reference angle \(\theta\)? What is the difference of these angles? Explain how this fact shows that the solutions of \(\tan \left(\theta\right)=k\), for \(k>0\), differ by \(\pi\).

133. What is the angle in the second quadrant with reference angle \(\theta\)? What is the angle in the fourth quadrant with reference angle \(\theta\)? What is the difference of these angles? Explain how this fact shows that the solutions \(\tan \left(\theta\right)=k\), for \(k<0\), differ by \(\pi\).

Applications

134. A sinusoidal function can approximate the population of deer in Marquette County over a typical year. The population reached a maximum of 50,000 deer on September 1^st and a minimum of 42,000 on March 1^st.

     1. Write a formula for the function \(P(t)\) that gives the deer population on the first of each month, where \(t=0\) is September 1.

     2. When is the deer population 45,000? Give exact expressions and approximations rounded to two decimal places.

     3. Graph your function over one period, and label the points that correspond to a deer population of 45,000. Is the population greater or less than 45,000 between the two solutions?

135. The percent of the moon visible from Earth is a sinusoidal function ranging from \(0 \%\) to \(100 \%\), with a period of 29.5 days.

     1. Write a formula for the function \(f(t)\) that gives the percent of the moon that is visible, if a new moon (\(0 \%\) visible) occurs at \(t=0\) days.

     2. When is \(25 \%\) of the moon visible? Give approximations rounded to two decimal places.

     3. Graph your function over one period, and label the points corresponding to a quarter moon. Is more or less than \(25 \%\) of the moon visible between the two solutions you found in part (b)?

136. A Ferris wheel has a diameter of 20 meters and completes one revolution every 60 seconds. Jorge is at the lowest position of the Ferris wheel, 1 meter above the ground, at \(t=0\) seconds.

     1. Write a formula for the function \(h(t)\) that gives Jorge's altitude in meters after \(t\) seconds.

     2. When is Jorge at an altitude of 18 meters during his first revolution? Give exact expressions and approximations rounded to two decimal places.

     3. Graph your function over one period, labeling the points that correspond to an altitude of 18 meters. Is Jorge above or below 18 meters between the two solutions you found in part (b)?

137. High tides occur every 12.2 hours at Point Lookout. The depth of the water at the end of Roy’s dock is 2.6 meters at high tide and 1.8 meters at low tide.

     1. Write a formula for the function \(d(t)\) that gives the depth of the water \(t\) hours after last night’s high tide.

     2. When is the water at the end of the dock 2 meters deep? Give exact approximations rounded to two decimal places.

     3. Graph your function over one period, labeling the points that correspond to a depth of 2 meters. Is the water depth greater or less than 2 meters between the two solutions you found in part (b)?