1.6: Hydrostatic Force and Pressure

Last updated
Save as PDF

Page ID: 130391

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Find the hydrostatic force against a submerged vertical plate.

In this section, we study hydrostatic force.

Hydrostatic Force and Pressure

Let's look at the force and pressure exerted on an object submerged in a liquid. Pressure, $ P $, is force per unit area. That is,

\[ P = \dfrac{F}{A}. \label{PFA} \]

Therefore, in the English system, we have pounds per square foot (or, perhaps more commonly, pounds per square inch, denoted psi). In the metric system we have newtons per square meter, also called pascals.

Let’s begin with the simple case of a plate of area $A$ submerged horizontally in water at a depth $s$ (Figure $\PageIndex{1}$). Then, the force exerted on the plate is simply the weight of the water above it, which is given by

\[F = \rho A s, \label{FrAs} \]

where $\rho$ is the volumetric density of water. To find the hydrostatic pressure - that is, the pressure exerted by water on a submerged object - we substitute $ F $ from Equation $ \ref{FrAs} $ into Equation $ \ref{PFA} $ so that

\[P = \dfrac{F}{A} = \dfrac{\rho A s}{A} = \rho s. \nonumber \]

This image has a circular plate submerged in water. The plate is labeled A and the depth of the water is labeled s. — Figure $\PageIndex{1}$: A plate submerged horizontally in water.

By Pascal’s principle, the pressure at a given depth is the same in all directions, so it does not matter if the plate is submerged horizontally or vertically. So, as long as we know the depth, we know the pressure. We can apply Pascal’s principle to find the force exerted on surfaces, such as dams, that are oriented vertically. We cannot, however, apply the Equation $ \ref{FrAs} $ directly, because the depth varies from point to point on a vertically-oriented surface. So, as we have done many times before, we form a partition, a Riemann sum, and, ultimately, a definite integral to calculate the force.

Suppose a thin plate is submerged in water. We choose our frame of reference such that the $x$-axis is oriented vertically, with the downward direction being positive, and point $x=0$ corresponding to a logical reference point.¹ Let $s(x)$ denote the depth at point $x$. Note we often let $x=0$ correspond to the surface of the water. In this case, depth at any point is simply given by $s(x)=x$. However, in some cases we may want to select a different reference point for $x=0$, so we proceed with the development in the more general case. Finally, let $w(x)$ denote the width of the plate at the point $x$.

Assume the top edge of the plate is at point $x=a$ and the bottom edge of the plate is at point $x=b$. Then, for $i=0,1,2, \ldots ,n$, let $P=\{x_i\}$ be a regular partition of the interval $[a,b]$, and for $i=1,2, \ldots ,n$, choose an arbitrary point $x^∗_i \in [x_{i−1},x_i]$. The partition divides the plate into several thin, rectangular strips (Figure $\PageIndex{2}$).

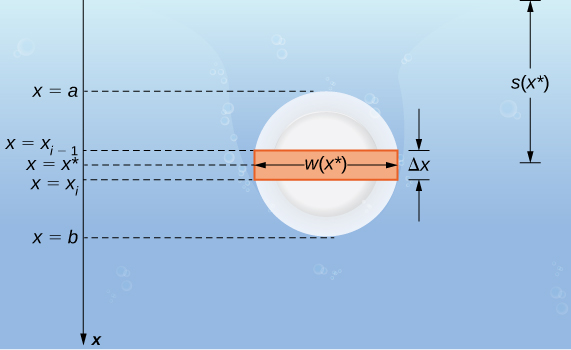
This image is the overhead view of a submerged circular plate. The x-axis is to the side of the plate. The plate’s diameter goes from x=a to x=b. There is a strip in the middle of the plate with thickness of delta x. On the axis this thickness begins at x=xsub(i-1) and ends at x=xsubi. The length of the strip in the plate is labeled w(csubi). — Figure $\PageIndex{2}$: A thin plate submerged vertically in water.

Let’s now estimate the force on a representative strip. If the strip is thin enough, we can treat it as if it is at a constant depth, $s(x^∗_i)$. We then have

\[F_i =\rho A s = \rho [w(x^∗_i) \Delta x] s(x^∗_i). \nonumber \]

Adding the forces, we get an estimate for the force on the plate:

\[F \approx \sum_{i=1}^n F_i = \sum_{i=1}^n \rho [w(x^∗_i) \Delta x] s(x^∗_i). \nonumber \]

This is a Riemann sum, so taking the limit gives us the exact force. We obtain

\[F = \lim_{n \to \infty }\sum_{i=1}^n \rho [w(x^∗_i) \Delta x] s(x^∗_i) = \int ^b_a \rho w(x) s(x) \, dx. \label{eqHydrostatic} \]

Evaluating this integral gives us the force on the plate. We summarize this in the following problem-solving strategy.

Problem-Solving Strategy: Finding Hydrostatic Force

Sketch a picture and select an appropriate frame of reference. (Note that if we select a frame of reference other than the one used earlier, we may have to adjust Equation \ref{eqHydrostatic} accordingly.)
Determine the depth and width functions, $s(x)$ and $w(x).$
Determine the weight density of whatever liquid with which you are working. The weight density of water is $62.4 \,\text{lb/ft}^3$, or $9800 \,\text{N/m}^3$.
Use the equation to calculate the total force.

Example $\PageIndex{1}$: Finding Hydrostatic Force

A water trough 15 ft long has ends shaped like inverted isosceles triangles, with base 8 ft and height 3 ft. Find the force on one end of the trough if the trough is full of water.

Solution

Figure $\PageIndex{3}$ shows the trough and a more detailed view of one end.

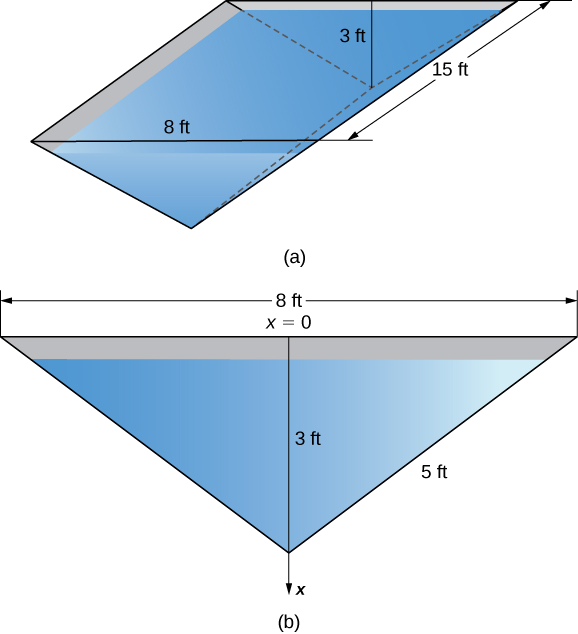
This figure has two images. The first is a water trough with rectangular sides. The length of the trough is 15 feet, the depth is 3 feet, and the width is 8 feet. The second image is a cross section of the trough. It is a triangle. The top has length of 8 feet and the sides have length 5 feet. The altitude is labeled with 3 feet. — Figure $\PageIndex{3}$: (a) A water trough with a triangular cross-section. (b) Dimensions of one end of the water trough.

Select a frame of reference with the $x$-axis oriented vertically and the downward direction being positive. Select the top of the trough as the point corresponding to $x=0$. The depth function, then, is $s(x)=x$. Using similar triangles, we see that $w(x) = 8 − \frac{8}{3} x$. Now, the weight density of water is $62.4 \,\text{lb/ft}^3$, so applying Equation \ref{eqHydrostatic}, we obtain

\[ \begin{array}{rcl}
F & = & \displaystyle \int ^b_a \rho w(x) s(x) \, dx \\
& = & \displaystyle \int ^3_0 62.4 \left(8−\dfrac{8}{3}x\right) x \,dx \\
& = & 62.4 \displaystyle \int ^3_0 \left(8x−\dfrac{8}{3}x^2 \right) \, dx \\
& = & 62.4 \left[4x^2−\dfrac{8}{9}x^3\right]\bigg|^3_0 \\
& \approx & 748.8. \\
\end{array} \nonumber \]

The water exerts a force of 748.8 lb on the end of the trough.

Exercise $\PageIndex{1}$

A water trough 12 m long has ends shaped like inverted isosceles triangles, with base 6 m and height 4 m. Find the force on one end of the trough if the trough is full of water.

Hint: Follow the problem-solving strategy and the process from the previous example.
Solution: $156,800$ N

Example $\PageIndex{2}$: Finding Hydrostatic Force

We now turn our attention to the Hoover Dam. The actual dam is arched, rather than flat, but we are going to make some simplifying assumptions to help us with the calculations. Assume the face of the Hoover Dam is shaped like an isosceles trapezoid with lower base 750 ft, upper base 1250 ft, and height 750 ft (see the following figure).

$This figure has two images. The first is a picture of a dam. The second image beside the dam is a trapezoidal figure representing the dimensions of the dam. The top is 1250 feet, the bottom is 750 feet. The height is 750 feet.$

When the reservoir is full, Lake Mead’s maximum depth is about 530 ft, and the surface of the lake is about 10 ft below the top of the dam (see the following figure).

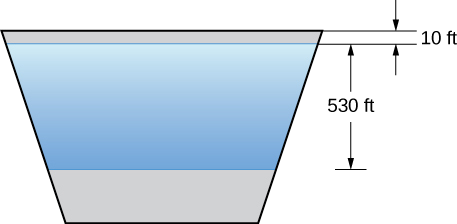
This figure is a trapezoid with the longer side on top. There is a smaller trapezoid inside the first with height labeled 530 feet. It is also 10 feet below the top of the larger trapezoid. — Figure $\PageIndex{4}$: A simplified model of the Hoover Dam with assumed dimensions.

Find the force on the face of the dam when the reservoir is full.
The southwest United States has been experiencing a drought, and the surface of Lake Mead is about 125 ft below where it would be if the reservoir were full. What is the force on the face of the dam under these circumstances?

Solution

We begin by establishing a frame of reference. As usual, we choose to orient the $x$-axis vertically, with the downward direction being positive. This time, however, we are going to let $x=0$ represent the top of the dam, rather than the surface of the water. When the reservoir is full, the surface of the water is $10$ ft below the top of the dam, so $s(x)=x−10$ (see the following figure).

This figure is a trapezoid with the longer side on top. There is a smaller trapezoid inside the first with height labeled s(x)=x-10. It represents the depth of the water. It is also 10 feet below the top of the larger trapezoid. The top of the larger trapezoid is at x=0. — Figure $\PageIndex{5}$: We first choose a frame of reference.

To find the width function, we again turn to similar triangles as shown in the figure below.

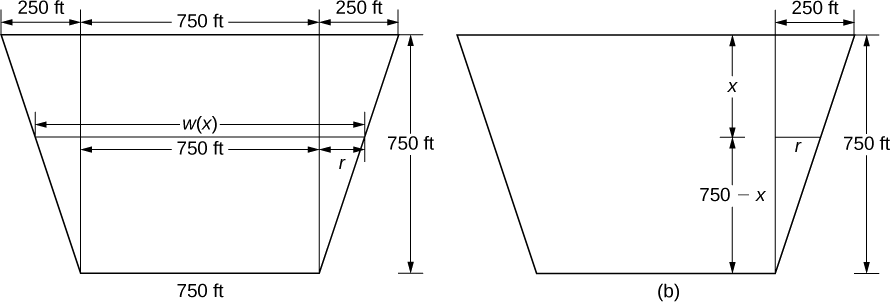
This figure has two images. The first is a trapezoid with larger side on the top. The length of the top is divided into 3 measures. The first measure is 250 feet, the second is 750 feet, and the third is 250 feet. The height of the trapezoid is 750 feet. The length of the bottom is 750 feet. Inside of the trapezoid the width is labeled w(x). Inside if one of the triangular sides is the width r. The second image is the same trapezoid. It has the height labeled as 750 feet. Inside the trapezoid it has the height divided into two segments. The first is labeled x, and the second is labeled 750-x. On the side of the trapezoid a triangle has been formed by a vertical line from the bottom side to the top. Inside of the triangle is a horizontal line segment labeled r. — Figure $\PageIndex{6}$: We use similar triangles to determine a function for the width of the dam. (a) Assumed dimensions of the dam; (b) highlighting the similar triangles.

From the figure, we see that $w(x)=750+2r$. Using properties of similar triangles, we get $r = 250 - \frac{1}{3} x$. Thus,

\[w(x) = 1250 - \dfrac{2}{3}x \nonumber \]

Using a weight density of $62.4 \, \text{lb/ft}^3 $ and applying Equation \ref{eqHydrostatic}, we get

\[\begin{array}{rcl}
F & = & \displaystyle \int^b_a \rho \, w(x) s(x) \, dx \\
& = & \displaystyle \int ^{540}_{10} 62.4 \left(1250−\dfrac{2}{3}x\right)(x−10) \, dx \\
& = & 62.4 \displaystyle \int ^{540}_{10}−\dfrac{2}{3}(x^2−1885x+18750)\,dx \\
& = & −62.4\left(\dfrac{2}{3}\right)\left(\dfrac{x^3}{3}−\dfrac{1885x^2}{2}+18750x\right) \bigg|^{540}_{10} \\
& \approx & 8,832,245,000 \,\text{lb} \\
& = & 4,416,122.5\,\text{tons}. \\
\end{array} \nonumber \]

Note the change from pounds to tons ($2000$lb = $1$ ton).

This changes our depth function, $s(x)$, and our limits of integration. We have $s(x)=x−135$. The lower limit of integration is 135. The upper limit remains $540$. Evaluating the integral, we get

\[\begin{array}{rcl}
F & = & \displaystyle \int^b_a \rho \, w(x) s(x) \, dx \\
& = & \displaystyle \int ^{540}_{135}62.4 \left(1250−\dfrac{2}{3}x\right)(x−135)\,dx \\
& = & −62.4(\dfrac{2}{3}) \displaystyle \int ^{540}_{135}(x−1875)(x−135)\,dx \\
& = & −62.4\left(\dfrac{2}{3}\right) \displaystyle \int ^{540}_{135}(x^2−2010x+253125)\,dx \\
& = & −62.4\left(\dfrac{2}{3}\right)\left(\dfrac{x^3}{3}−1005x^2+253125x\right)\bigg|^{540}_{135} \\
& \approx & 5,015,230,000\,\text{lb} \\
& = & 2,507,615\,\text{tons}. \\
\end{array} \nonumber \]

Exercise $\PageIndex{2}$

When the reservoir is at its average level, the surface of the water is about 50 ft below where it would be if the reservoir were full. What is the force on the face of the dam under these circumstances?

Hint: Change the depth function, $s(x),$ and the limits of integration.
Solution: Approximately 7,164,520,000 lb or 3,582,260 t

Subsection Footnotes

¹ As before, you could treat this entire subsection using the standard coordinate system. The reader is trusted with being able to derive the relevant mechanics.

Key Concepts

Several physical applications of the definite integral are common in engineering and physics.
Definite integrals can be used to determine the mass of an object if its density function is known.
Work can also be calculated from integrating a force function, or when counteracting the force of gravity, as in a pumping problem.
Definite integrals can also be used to calculate the force exerted on an object submerged in a liquid.

Key Equations

Mass of a one-dimensional object

$ m=\int ^b_a\rho(x)dx$

Mass of a circular object

$ m=\int ^r_02 \pi x\rho(x)dx$

Work done on an object

$ W=\int ^b_aF(x)dx$

Hydrostatic force on a plate

$ F=\int ^b_a\rho w(x)s(x)dx$

Glossary

density function: a density function describes how mass is distributed throughout an object; it can be a linear density, expressed in terms of mass per unit length; an area density, expressed in terms of mass per unit area; or a volume density, expressed in terms of mass per unit volume; weight-density is also used to describe weight (rather than mass) per unit volume
Hooke’s law: this law states that the force required to compress (or elongate) a spring is proportional to the distance the spring has been compressed (or stretched) from equilibrium; in other words, $F=kx$, where $k$ is a constant
hydrostatic pressure: the pressure exerted by water on a submerged object
work: the amount of energy it takes to move an object; in physics, when a force is constant, work is expressed as the product of force and distance

Search

Text Color

Text Size

Margin Size

Font Type

Problem-Solving Strategy: Finding Hydrostatic Force

Example \(\PageIndex{1}\): Finding Hydrostatic Force

Solution

Exercise \(\PageIndex{1}\)

Example \(\PageIndex{2}\): Finding Hydrostatic Force

Solution

Exercise \(\PageIndex{2}\)

Subsection Footnotes