1.8E: Exercises

In exercises 1 - 4, find the weight of the one-dimensional object.

1) A wire that is $2$ ft long (starting at $x=0$) and has a weight density function of $\gamma(x)=x^2+2x$ lb/ft

2) A car antenna that is $3$ ft long (starting at $x=0)$ and has a weight density function of $\gamma(x)=3x+2$ lb/ft

Answer

$\frac{39}{2}$ lbs.

3) A metal rod that is $8$ in. long (starting at $x=0$) and has a weight density function of $\gamma(x)=e^{1/2x}$ lb/in.

4) A pencil that is $4$ in. long (starting at $x=2$) and has a weight density function of $\gamma(x)=\dfrac{5}{x}$ oz/in.

Answer

$\ln(243)$ oz.

5) Using the Left Endpoint Method with $n = 6$, approximate the weight of a one-dimensional ruler that is $12$ in. long (starting at $x=5$) and has a weight density function of $\gamma(x)=\ln(x)+(1/2)x^2$ oz/in.

In exercises 6 - 7, find the weight of the two-dimensional object that is centered at the origin.

6) An oversized hockey puck of radius $2$ in. with radial weight density function $\gamma(x)=x^3−2x+5$ $\text{lb}/\text{in}^2$.

Answer

$\frac{332\pi }{15}$ lbs.

7) A disk of radius $5$ cm with radial weight density function $\gamma(x)=\sqrt{3x}$ $\text{g}/\text{cm}^2$

Answer

$20\pi \sqrt{15}$ g.

8) Using the Right Endpoint Method with $n = 6$, approximate the weight of a two-dimensional frisbee (centered at the origin) of radius $6$ in. with radial weight density function $\gamma(x)=e^{−x}$ $\text{oz}/\text{in}^2$.

In exercises 9 - 14, calculate the center of mass for the collection of masses given.

9) $m_1=2$ at $x_1=1$ and $m_2=4$ at $x_2=2$

10) $m_1=1$ at $x_1=−1$ and $m_2=3$ at $x_2=2$

Answer

$x = \frac{5}{4}$

11) $m=3$ at $x=0,1,2,6$

12) Unit masses at $(x,y)=(1,0),(0,1),(1,1)$

Answer

$\left(\frac{2}{3},\, \frac{2}{3}\right)$

13) $m_1=1$ at $(1,0)$ and $m_2=4$ at $(0,1)$

14) $m_1=1$ at $(1,0)$ and $m_2=3$ at $(2,2)$

Answer

$\left(\frac{7}{4},\,\frac{3}{2}\right)$

In exercises 15 - 24, compute the center of mass $\bar x.$

15) $\rho =1$ for $x \in (−1,3)$

16) $\rho =x^2$ for $x \in (0,L)$

Answer

$\dfrac{3L}{4}$

17) $\rho =1$ for $x \in (0,1)$ and $\rho =2$ for $x \in (1,2)$

18) $\rho =\sin x$ for $x \in (0, \pi )$

Answer

$\frac{ \pi }{2}$

19) $\rho =\cos x$ for $x \in \left(0,\frac{ \pi }{2}\right)$

20) $\rho =e^x$ for $x \in (0,2)$

Answer

$\dfrac{e^2+1}{e^2−1}$

21) $\rho =x^3+xe^{−x}$ for $x \in (0,1)$

22) $\rho =x\sin x$ for $x \in (0, \pi )$

Answer

$\dfrac{ \pi ^2−4}{ \pi }$

23) $\rho =\sqrt{x}$ for $x \in (1,4)$

24) $\rho =\ln x$ for $x \in (1,e)$

Answer

$\frac{1}{4}(1+e^2)$

In exercises 25 - 27, compute the center of mass $(\bar{x},\bar{y}).$ Use symmetry to help locate the center of mass whenever possible.

25) $\rho =7$ in the square $0 \leq x \leq 1, \; 0 \leq y \leq 1$

26) $\rho =3$ in the triangle with vertices $(0,0), \, (a,0)$, and $(0,b)$

Answer

$\left(\frac{a}{3},\, \frac{b}{3}\right)$

27) $\rho =2$ for the region bounded by $y=\cos(x), \; y=−\cos(x), \; x=−\frac{ \pi }{2}$, and $x=\frac{ \pi }{2}$

In exercises 28 - 34, use a calculator to draw the region, then compute the center of mass $(\bar{x},\bar{y}).$ Use symmetry to help locate the center of mass whenever possible.

28) [Technology Required] The region bounded by $y=\cos(2x), \; x=−\frac{ \pi }{4}$, and $x=\frac{ \pi }{4}$

Answer

$\left(0,\frac{ \pi }{8}\right)$

29) [Technology Required] The region between $y=2x^2, \; y=0, \; x=0,$ and $x=1$

30) [Technology Required] The region between $y=\frac{5}{4}x^2$ and $y=5$

Answer

$(0,3)$

31) [Technology Required] Region between $y=\sqrt{x}, \; y=\ln x, \; x=1,$ and $x=4$

32) [Technology Required] The region bounded by $y=0$ and $\dfrac{x^2}{4}+\dfrac{y^2}{9}=1$

Answer

$\left(0,\frac{4}{ \pi }\right)$

33) [Technology Required] The region bounded by $y=0, \; x=0,$ and $\dfrac{x^2}{4}+\dfrac{y^2}{9}=1$

34) [Technology Required] The region bounded by $y=x^2$ and $y=x^4$ in the first quadrant

Answer

$\left(\frac{5}{8},\, \frac{1}{3}\right)$

In exercises 35 - 39, use the Theorem of Pappus to determine the volume of the shape.

35) Rotating $y=mx$ around the $x$-axis between $x=0$ and $x=1$

36) Rotating $y=mx$ around the $y$-axis between $x=0$ and $x=1$

Answer

$V = \frac{m \pi }{3}$ units³

37) A general cone created by rotating a triangle with vertices $(0,0), \, (a,0),$ and $(0,b)$ around the $y$-axis. Does your answer agree with the volume of a cone?

38) A general cylinder created by rotating a rectangle with vertices $(0,0), \, (a,0), \, (0,b),$ and $(a,b)$ around the $y$-axis. Does your answer agree with the volume of a cylinder?

Answer

$V = \pi a^2b$ units³

39) A sphere created by rotating a semicircle with radius $a$ around the $y$-axis. Does your answer agree with the volume of a sphere?

In exercises 40 - 44, use a calculator to draw the region enclosed by the curve. Find the area $M$ and the centroid $(\bar{x},\bar{y})$ for the given shapes. Use symmetry to help locate the center of mass whenever possible.

40) [Technology Required] Quarter-circle: $y=\sqrt{1−x^2}, \; y=0$, and $x=0$

Answer

$\left(\frac{4}{3 \pi },\, \frac{4}{3 \pi }\right)$

41) [Technology Required] Triangle: $y=x, \; y=2−x$, and $y=0$

42) [Technology Required] Lens: $y=x^2$ and $y=x$

Answer

$\left(\frac{1}{2},\, \frac{2}{5}\right)$

43) [Technology Required] Ring: $y^2+x^2=1$ and $y^2+x^2=4$

44) [Technology Required] Half-ring: $y^2+x^2=1, \; y^2+x^2=4,$ and $y=0$

Answer

$\left(0,\, \frac{28}{9 \pi }\right)$

45) Find the generalized center of mass in the sliver between $y=x^a$ and $y=x^b$ with $a>b$. Then, use the Pappus theorem to find the volume of the solid generated when revolving around the $y$-axis.

46) Find the generalized center of mass between $y=a^2−x^2, \; x=0$, and $y=0$. Then, use the Pappus theorem to find the volume of the solid generated when revolving around the $y$-axis.

Answer

Center of mass: $\left(\frac{a}{6},\,\frac{4a^2}{5}\right),$
Volume: $\dfrac{2 \pi a^4}{9}$ units³

47) Find the generalized center of mass between $y=b\sin(ax),\; x=0,$ and $x=\dfrac{ \pi }{a}.$ Then, use the Theorem of Pappus to find the volume of the solid generated when revolving around the $y$-axis.

48) Use the Theorem of Pappus to find the volume of a torus (pictured here). Assume that a disk of radius $a$ is positioned with the left end of the circle at $x=b, \, b>0,$ and is rotated around the $y$-axis.

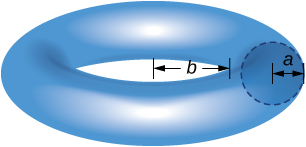
Answer

Volume: $V = 2\pi^2a^2(b+a)$

49) Find the center of mass $(\bar{x},\bar{y})$ for a thin wire along the semicircle $y=\sqrt{1−x^2}$ with unit mass. (Hint: Use the Theorem of Pappus.)

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.