3.3: The Divergence and Integral Tests

Learning Objectives

• Use the Divergence Test to determine whether a series converges or diverges.
• Use the Integral Test to determine the convergence of a series.
• Estimate the value of a series by finding bounds on its remainder term.

In the previous section, we determined the convergence or divergence of several series by explicitly calculating the limit of the sequence of partial sums \( \{S_k\}\). In practice, explicitly calculating this limit can be difficult or impossible. Luckily, several tests exist that allow us to determine convergence or divergence for many types of series. In this section, we discuss two of these tests: the Divergence Test and the Integral Test. We will examine several other tests in the rest of this chapter and then summarize how and when to use them.

---

Divergence Test

We begin our exploration of tests for the convergence or divergence of series with the test that is the quickest to use.

Theorem: Divergence Test

If \(\displaystyle \lim_{n \to \infty }a_n \neq 0\) or \(\displaystyle \lim_{n \to \infty }a_n\) does not exist, then the series \(\displaystyle \sum_{n=1}^ \infty a_n\) diverges.

Proof by Contraposition.¹

Suppose \(\displaystyle \sum_{n=1}^ \infty a_n\) converges. Let \( S_n = a_1 + a_2 + \cdots + a_n \). Then \( a_n = S_n - S_{n - 1} \).² Since we have assumed \(\displaystyle \sum_{n=1}^ \infty a_n\) converges, the sequence of partial sums, \( \{ S_n \} \) must be convergent. Let \( \displaystyle \lim_{n \to \infty} S_n = S \). Since \( n - 1 \to \infty \) as \( n \to \infty \), we also have \( \displaystyle \lim_{n \to \infty} S_{n - 1} = S \). Therefore\[ \lim_{n \to \infty} a_n = \lim_{n \to \infty} \left( S_n - S_{n - 1} \right) = \lim_{n \to \infty} S_n - \lim_{n \to \infty} S_{n - 1} = S - S = 0. \nonumber \]Hence, the limit \( \lim_{n \to \infty} a_n \) exists and is \( 0 \).³

As with all of the proofs in Calculus, it is worthwhile to read through the proof of the Divergence Test and try to understand it. The method used (proof by contraposition) is a wonderful indirect proof style.

Caution

It is important to note that the converse of the Divergence Test is not true. That is, if \(\displaystyle \lim_{n \to \infty }a_n=0\), we cannot make any conclusion about the convergence of \(\displaystyle \sum_{n=1}^ \infty a_n\).

To illustrate that cautionary statement, consider the harmonic series \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n}\).

\(\displaystyle \lim_{n \to 0}\frac{1}{n}=0\), but the harmonic series \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n}\) diverges. In this section and the remaining sections of this chapter, we show many more examples of such series. Consequently, although we can use the Divergence Test to show that a series diverges, we cannot use it to prove that a series converges. Specifically, if \( a_n \to 0\), the Divergence Test is inconclusive.

Example \( \PageIndex{1}\): Using the Divergence Test

For each of the following series, apply the Divergence Test. If the Divergence Test proves that the series diverges, state so. Otherwise, indicate that the Divergence Test is inconclusive.

1. \(\displaystyle \sum^ \infty _{n=1}\frac{n}{3n−1}\)
2. \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^3}\)
3. \(\displaystyle \sum^ \infty _{n=1}e^{1/n^2}\)

Solution

1. Since \(\displaystyle \lim_{n \to \infty } \frac{n}{3n−1}=\frac{1}{3} \neq 0\), by the Divergence Test, we can conclude that \(\displaystyle \sum_{n=1}^ \infty \dfrac{n}{3n−1}\) diverges.
2. Since \(\displaystyle \lim_{n \to \infty } \frac{1}{n^3}=0\), the Divergence Test is inconclusive.
3. Since \(\displaystyle \lim_{n \to \infty } e^{1/n^2}=1 \neq 0\), by the Divergence Test, the series \(\displaystyle \sum_{n=1}^ \infty e^{1/n^2}\) diverges.

Exercise \( \PageIndex{1}\)

What does the Divergence Test tell us about the series \(\displaystyle \sum_{n=1}^ \infty \cos(1/n^2)\)?

Hint

Look at \(\displaystyle \lim_{n \to \infty }\cos(1/n^2)\).

Answer

The series diverges.

Subsection Footnotes

¹ Most theorems can be stated symbolically as the conditional proposition\( P \implies Q \), where \( P \) is a statement called the antecedent, and \( Q \) is a statement called the consequent. Instead of proving \( P \implies Q \) directly, it is sometimes easier to prove it indirectly. There are two kinds of indirect proofs: proof by contradiction, and proof by contraposition.

You have already seen proofs by contradiction (see the uses of Rolle's Theorem in Calculus I for proving that a given equation has exactly one root). In a proof by contraposition, we use the fact that an implication, "if \( P \), then \( Q \)," is equivalent to its contrapositive, "if not \( Q \), then not \( P \)" (the notation, \( \sim P \), is called the negation of \( P \)). Therefore, instead of proving \( P \implies Q \), we may prove its contrapositive \( \sim Q \implies \sim P \). Since it is an implication, we could use a direct proof at this point:

Assume \( \sim Q \) is true (hence, assume \( Q \) is false). Show that \( \sim P \) is true (that is, show that \( P \) is false).

² It can be useful at times to remember that \( S_n = S_{n - 1} + a_n \).

³ The negation of "\( A \) or \( B \)" is "not \( A \) and not \( B \)."

---

Integral Test

In the previous section, we proved that the harmonic series diverges by looking at the sequence of partial sums \( \{S_k\}\) and showing that \( S_{2^k} \gt 1+k/2\) for all \( k \in \mathbb{N} \). In this section we use a different technique to prove the divergence of the harmonic series. This technique is important because it is used to prove the divergence or convergence of many other series. This test, called the Integral Test, compares an infinite sum to an improper integral. It is important to note that this test can only be applied when we are considering a series whose terms are all positive.

To illustrate how the Integral Test works, use the harmonic series as an example. In Figure \(\PageIndex{1}\), we depict the harmonic series by sketching a sequence of rectangles with areas \( 1, 1/2, 1/3, 1/4, \ldots \) along with the function \( f(x)=1/x\).

Figure \(\PageIndex{1}\): The sum of the areas of the rectangles is greater than the area between the curve \( f(x)=1/x\) and the \( x\)-axis for \( x \geq 1\). Since the area bounded by the curve is infinite (as calculated by an improper integral), the sum of the areas of the rectangles is also infinite.

From the graph, we see that

\[\sum_{n=1}^k\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+ \cdots +\dfrac{1}{k} \gt \int ^{k+1}_1\dfrac{1}{x}\,dx. \nonumber \]

Therefore, for each \( k\), the \( k^{\text{th}}\) partial sum \( S_k\) satisfies

\[\begin{array}{rcl}
S_k & = & \displaystyle \sum_{n=1}^k\dfrac{1}{n} \\
& \gt & \displaystyle \int^{k+1}_1\dfrac{1}{x}\,dx \\
& = & \ln x \big| ^{k+1}_1 \\
& = & \ln (k+1)−\ln (1) \\
& = & \ln (k+1). \\
\end{array} \nonumber \]

Since \(\displaystyle \lim_{k \to \infty }\ln(k+1)= \infty\), we see that the sequence of partial sums \( \{S_k\}\) is unbounded. Therefore, \( \{S_k\}\) diverges, and, consequently, the series \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n}\) also diverges.

Now consider the series \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n^2}\). We show how an integral can be used to prove that this series converges. In Figure \(\PageIndex{2}\), we sketch a sequence of rectangles with areas \( 1, 1/2^2, 1/3^2, \ldots \) along with the function \( f(x)=\frac{1}{x^2}\).

Figure \(\PageIndex{2}\): The sum of the areas of the rectangles is less than the sum of the area of the first rectangle and the area between the curve \( f(x)=1/x^2\) and the \( x\)-axis for \( x \geq 1\). Since the area bounded by the curve is finite, the sum of the areas of the rectangles is also finite.

From the graph we see that

\[\sum_{n=1}^k\dfrac{1}{n^2}=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+ \cdots +\dfrac{1}{k^2} \lt 1+ \int ^k_1\dfrac{1}{x^2}\,dx. \nonumber \]

Therefore, for each \( k\), the \( k^{\text{th}}\) partial sum \( S_k\) satisfies

\[\begin{array}{rcl}
S_k & = & \sum_{n=1}^k\dfrac{1}{n^2} \\
& \lt & 1+ \int ^k_1\dfrac{1}{x^2}\,dx \\
& = & 1 − \dfrac{1}{x} \bigg|^k_1 \\
& = & 1 − \dfrac{1}{k}+1 \\
& = & 2−\dfrac{1}{k} \\
& \lt & 2. \\
\end{array} \nonumber \]

We conclude that the sequence of partial sums \( \{S_k\}\) is bounded. Moreover, since

\[S_k = S_{k−1}+\dfrac{1}{k^2} \nonumber \]

for \( k \geq 2\), the sequence of partial sums is also increasing. Therefore, by the Monotone Convergence Theorem, it converges. Thus, the series \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n^2}\) converges.

We can extend this idea to prove convergence or divergence for many different series. Suppose \(\displaystyle \sum^ \infty _{n=1}a_n\) is a series with positive terms \( a_n\) such that there exists a continuous, positive, decreasing function \( f\) where \( f(n)=a_n\) for all positive integers. Then, as in Figure \(\PageIndex{3a}\), for any integer \( k\), the \( k^{\text{th}}\) partial sum \( S_k\) satisfies

\[S_k=a_1+a_2+a_3+ \cdots +a_k \lt a_1+ \int ^k_1f(x)\,dx \lt 1+ \int ^ \infty _1f(x)\,dx. \nonumber \]

Figure \(\PageIndex{3}\): (a) If we can inscribe rectangles inside a region bounded by a curve \( y=f(x)\) and the \( x\)-axis, and the area bounded by those curves for \( x \geq 1\) is finite, then the sum of the areas of the rectangles is also finite. (b) If a set of rectangles circumscribes the region bounded by \( y=f(x)\) and the \( x\) axis for \( x \geq 1\) and the region has infinite area, then the sum of the areas of the rectangles is also infinite.

Therefore, if \(\displaystyle \int ^ \infty _1f(x)\,dx\) converges, then the sequence of partial sums \( \{S_k\}\) is bounded. Since \( \{S_k\}\) is an increasing sequence, if it is also a bounded sequence, then by the Monotone Convergence Theorem, it converges. We conclude that if \(\displaystyle \int ^ \infty _1f(x)\,dx\) converges, then the series \(\displaystyle \sum^ \infty _{n=1}a_n\) also converges.

On the other hand, from Figure \(\PageIndex{3b}\), for any integer \( k\), the \( k^{\text{th}}\) partial sum \( S_k\) satisfies

\[S_k=a_1+a_2+a_3+ \cdots +a_k> \int ^{k+1}_1f(x)\,dx. \nonumber \]

If

\[ \lim_{k \to \infty } \int ^{k+1}_1f(x)\,dx= \infty , \nonumber \]

then \( \{S_k\}\) is an unbounded sequence and therefore diverges. As a result, the series \(\displaystyle \sum_{n=1}^ \infty a_n\) also diverges. Since \( f\) is a positive function, if \(\displaystyle \int ^ \infty _1f(x)\,dx\) diverges, then

\[ \lim_{k \to \infty } \int ^{k+1}_1f(x)\,dx= \infty . \nonumber \]

We conclude that if \(\displaystyle \int ^ \infty _1f(x)\,dx\) diverges, then \(\displaystyle \sum_{n=1}^ \infty a_n\) diverges.

Theorem: Integral Test

Suppose \(\displaystyle \sum_{n=1}^ \infty a_n\) is a series with positive terms \( a_n\). Suppose there exists a function \( f\) and a positive integer \( N\) such that the following three conditions are satisfied:

1. \( f\) is continuous,
2. \( f\) is decreasing, and
3. \( f(n)=a_n\) for all integers \( n \geq N\).

Then

\[\sum_{n=1}^ \infty a_n \nonumber \]

and

\[ \int ^ \infty _Nf(x)\,dx \nonumber \]

both converge or both diverge (Figure \(\PageIndex{3}\)).

Caution

The base sequence, \( \{ a_n \} \), in the Integral Test must eventually consist of non-negative terms only. That is, to be able to use the Integral Test, there must exist \( N \) such that \( f(n) = a_n \geq 0 \) for all \( n \geq N \). This (along with the need to evaluate an improper integral) is a weakness of the Integral Test, and a reason we will eventually need to consider other tests for convergence.

Although convergence of \(\displaystyle \int ^ \infty _Nf(x)\,dx\) implies convergence of the related series \(\displaystyle \sum_{n=1}^ \infty a_n\), it does not imply that the value of the integral and the series are the same. They may be different, and often are. For example,

\[\sum_{n=1}^ \infty \left(\dfrac{1}{e}\right)^n=\dfrac{1}{e}+\left(\dfrac{1}{e}\right)^2+\left(\dfrac{1}{e}\right)^3+ \cdots \nonumber \]

is a geometric series with initial term \( a=1/e\) and ratio \( r=1/e,\) which converges to

\[\dfrac{1/e}{1−(1/e)}=\dfrac{1/e}{(e−1)/e}=\dfrac{1}{e−1}. \nonumber \]

However, the related integral \(\displaystyle \int ^ \infty _1(1/e)^x\,dx\) satisfies

\[ \int ^ \infty _1\left(\frac{1}{e}\right)^x\,dx= \int ^ \infty _1e^{−x}\,dx=\lim_{b \to \infty } \int ^b_1e^{−x}\,dx=\lim_{b \to \infty }−e^{−x}\big|^b_1=\lim_{b \to \infty }[−e^{−b}+e^{−1}]=\dfrac{1}{e}. \nonumber \]

Example \( \PageIndex{2}\): Using the Integral Test

For each of the following series, use the Integral Test to determine whether the series converges or diverges.

1. \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n^3}\)
2. \(\displaystyle \sum^ \infty _{n=1}\frac{1}{\sqrt{2n−1}}\)

Solution

a. Compare

\[\sum_{n=1}^ \infty \dfrac{1}{n^3} \text{ and } \int ^ \infty _1\dfrac{1}{x^3}\,dx. \nonumber \]

We have

\[ \begin{array}{rcl}
\displaystyle \int^\infty_1 \dfrac{1}{x^3}\,dx & = & \displaystyle \lim_{b \to \infty } \int ^b_1\dfrac{1}{x^3}\,dx \\
& = & \displaystyle \lim_{b \to \infty }\left[−\dfrac{1}{2x^2}\bigg|^b_1\right] \\
& = & \displaystyle \lim_{b \to \infty }\left[−\dfrac{1}{2b^2}+\dfrac{1}{2}\right] \\
& = & \dfrac{1}{2}. \\
\end{array} \nonumber \]

Thus the integral \(\displaystyle \int ^ \infty _1\frac{1}{x^3}\,dx\) converges, and therefore so does the series

\[ \sum_{n=1}^ \infty \dfrac{1}{n^3}. \nonumber \]

b. Compare

\[ \sum_{n=1}^ \infty \dfrac{1}{\sqrt{2n−1}} \text{ and } \int ^ \infty _1\dfrac{1}{\sqrt{2x−1}}\,dx. \nonumber \]

Since

\[ \begin{array}{rcl}
\displaystyle \int ^ \infty _1\frac{1}{\sqrt{2x−1}}\,dx & = & \displaystyle \lim_{b \to \infty } \int ^b_1\frac{1}{\sqrt{2x−1}}\,dx \\
& = & \displaystyle \lim_{b \to \infty }\sqrt{2x−1}\bigg|^b_1 \\
& = & \displaystyle \lim_{b \to \infty }\left[\sqrt{2b−1}−1\right] \\
& = & \infty, \\
\end{array} \nonumber \]

the integral \(\displaystyle \int ^ \infty _1\frac{1}{\sqrt{2x−1}}\,dx\) diverges, and therefore

\[ \sum_{n=1}^ \infty \frac{1}{\sqrt{2n−1}} \nonumber \]

diverges.

Exercise \( \PageIndex{2}\)

Use the Integral Test to determine whether the series \(\displaystyle \sum^ \infty _{n=1}\frac{n}{3n^2+1}\) converges or diverges.

Hint

Compare to the integral \(\displaystyle \int ^ \infty _1\frac{x}{3x^2+1}\,dx.\)

Answer

The series diverges.

---

The \(p\)-Series

The harmonic series \(\displaystyle \sum^ \infty _{n=1}1/n\) and the series \(\displaystyle \sum^ \infty _{n=1}1/n^2\) are both examples of a type of series called a \(p\)-series.

Definition: \(p\)-series

For any real number \( p\), the series

\[\sum_{n=1}^ \infty \dfrac{1}{n^p} \nonumber \]

is called a \(p\)-series.

We know the \(p\)-series converges if \( p=2\) and diverges if \( p=1\). What about other values of \( p\)? In general, it is difficult, if not impossible, to compute the exact value of most \( p\)-series. However, we can use the tests presented thus far to prove whether a \( p\)-series converges or diverges.

If \( p \lt 0\), then \( 1/n^p \to \infty\), and if \( p=0\), then \( 1/n^p \to 1\). Therefore, by the Divergence Test,

\[\sum_{n=1}^ \infty \dfrac{1}{n^p} \nonumber \]

diverges if \(p \leq 0\).

If \( p \gt 0\), then \( f(x)=1/x^p\) is a positive, continuous, decreasing function. Therefore, for \( p \gt 0\), we use the Integral Test, comparing

\[\sum_{n=1}^ \infty \dfrac{1}{n^p} \text{ and } \int ^ \infty _1\dfrac{1}{x^p}\,dx. \nonumber \]

We have already considered the case when \( p=1\). Here we consider the case when \( p \gt 0, p \neq 1\). For this case,

\[ \begin{array}{rcl}
\displaystyle \int ^ \infty _1\dfrac{1}{x^p}\,dx & = & \displaystyle \lim_{b \to \infty } \int ^b_1\dfrac{1}{x^p}\,dx \\
& = & \displaystyle \lim_{b \to \infty }\dfrac{1}{1−p}x^{1−p}\bigg|^b_1 \\
& = & \displaystyle \lim_{b \to \infty }\dfrac{1}{1−p}[b^{1−p}−1]. \\
\end{array} \nonumber \]

Because \( b^{1−p} \to 0\) if \( p \gt 1\) and \( b^{1−p} \to \infty \) if \( p \lt 1\), we conclude that

\[ \int ^ \infty _1\dfrac{1}{x^p}\,dx=\begin{cases}\dfrac{1}{p−1}, \text{if}\;p>1\\ \infty , \text{if}\;p<1.\end{cases} \nonumber \]

Therefore, \(\displaystyle \sum^ \infty _{n=1}1/n^p\) converges if \( p>1\) and diverges if \( 0<p<1\). We summarize this as a theorem.

Theorem: \( p \)-series Test

The \( p \)-series

\[ \sum_{n = 1}^{\infty} \dfrac{1}{n^p} \nonumber \]

converges if and only if \( p \gt 1 \). It diverges otherwise.

Example \( \PageIndex{3}\): Testing for Convergence of p-series

For each of the following series, determine whether it converges or diverges.

1. \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^4}\)
2. \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^{2/3}}\)

Solution

1. This is a \(p\)-series with \( p=4>1\), so the series converges.
2. Since \( p=2/3<1\), the series diverges.

Exercise \( \PageIndex{3}\)

Does the series \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^{5/4}}\) converge or diverge?

Hint

\( p=5/4\)

Answer

The series converges.

---

Estimating the Value of a Series

Suppose we know that a series \(\displaystyle \sum_{n=1}^ \infty a_n\) converges and we want to estimate the sum of that series. Certainly we can approximate that sum using any finite sum \(\displaystyle \sum_{n=1}^N a_n\) where \( N \in \mathbb{N}\). The question we address here is, for a convergent series \(\displaystyle \sum^ \infty _{n=1}a_n\), how good is the approximation \(\displaystyle \sum^N_{n=1}a_n\)?

More specifically, if we let

\[R_N = \sum_{n=1}^ \infty a_n−\sum_{n=1}^N a_n \nonumber \]

be the remainder when the sum of an infinite series is approximated by the \(N^{\text{th}}\) partial sum, how large is \( R_N\)? For some types of series, we are able to use the ideas from the Integral Test to estimate \( R_N\).

Theorem: Remainder Estimate from the Integral Test

Suppose \(\displaystyle \sum^ \infty _{n=1}a_n\) is a convergent series with positive terms.⁴ Suppose there exists a function \( f\) satisfying the following three conditions:

1. \( f\) is continuous,
2. \( f\) is decreasing, and
3. \( f(n)=a_n\) for all integers \( n \geq 1\).

Let \( S_N\) be the \(N^{\text{th}}\) partial sum of \(\displaystyle \sum^ \infty _{n=1}a_n\). For all \( N \in \mathbb{N}\),

\[S_N + \int^\infty_{N+1} f(x) \, dx \lt \sum_{n=1}^\infty a_n \lt S_N + \int ^ \infty _Nf(x)\,dx. \nonumber \]

In other words, the remainder \(\displaystyle R_N=\sum^ \infty _{n=1}a_n−S_N=\sum^ \infty _{n=N+1}a_n\) satisfies the following estimate:

\[ \int ^ \infty _{N+1}f(x)\,dx<R_N< \int ^ \infty _Nf(x)\,dx. \nonumber \]

This is known as the remainder estimate.

The remainder estimate can be thought of as the error in our approximation of the value of the series.

We illustrate this theorem in Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): Given a continuous, positive, decreasing function \( f\) and a sequence of positive terms \( a_n\) such that \( a_n=f(n)\) for all \( n \in \mathbb{N}\), (a) the areas \(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+ \cdots \lt \int ^ \infty _Nf(x)\,dx\), or (b) the areas \(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+ \cdots \gt \int ^ \infty _{N+1}f(x)\,dx\). Therefore, the integral is either an overestimate or an underestimate of the error.

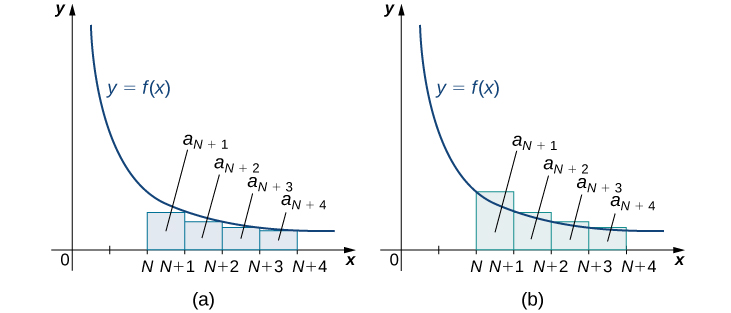
In particular, by representing the remainder \( R_N=a_{N+1}+a_{N+2}+a_{N+3}+ \cdots \) as the sum of areas of rectangles, we see that the area of those rectangles is bounded above by \(\displaystyle \int ^ \infty _Nf(x)\,dx\) and bounded below by \(\displaystyle \int ^ \infty _{N+1}f(x)\,dx.\) In other words,

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+ \cdots \gt \int ^ \infty _{N+1}f(x)\,dx \nonumber \]

and

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+ \cdots \lt \int ^ \infty _Nf(x)\,dx. \nonumber \]

We conclude that

\[ \int ^ \infty _{N+1}f(x)\,dx \lt R_N \lt \int ^ \infty _Nf(x)\,dx. \nonumber \]

Since

\[\sum_{n=1}^ \infty a_n=S_N+R_N, \nonumber \]

where \( S_N\) is the \(N^{\text{th}}\) partial sum, we conclude that

\[S_N+ \int ^ \infty _{N+1}f(x)\,dx \lt \sum_{n=1}^ \infty a_n \lt S_N+ \int ^ \infty _Nf(x)\,dx. \nonumber \]

Having the ability to approximate the value of a series is important, and we will use different approximation methods for different convergence tests as we move forward.

Example \( \PageIndex{4}\): Estimating the Value of a Series

Consider the series \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^3}\).

1. Calculate \(\displaystyle S_{10}=\sum^{10}_{n=1}\frac{1}{n^3}\) and estimate the error.
2. Determine the least value of \( N\) necessary such that \( S_N\) will estimate \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^3}\) to within \( 0.001\).

Solution

a. Using technology, we have

\[ S_{10}=1+\dfrac{1}{2^3}+\dfrac{1}{3^3}+\dfrac{1}{4^3}+ \cdots +\dfrac{1}{10^3} \approx 1.19753. \nonumber \]

By the remainder estimate, we know

\[ R_N \lt \int ^ \infty _N\dfrac{1}{x^3}\,dx. \nonumber \]

We have

\[ \begin{array}{rcl}
\displaystyle \int ^ \infty _{10}\dfrac{1}{x^3}\,dx & = & \displaystyle \lim_{b \to \infty } \int ^b_{10}\dfrac{1}{x^3}\,dx \\
& = & \displaystyle \lim_{b \to \infty }\left[−\dfrac{1}{2x^2}\right]^b_N \\
& = & \displaystyle \lim_{b \to \infty }\left[−\dfrac{1}{2b^2}+\dfrac{1}{2N^2}\right] \\
& = & \dfrac{1}{2N^2}. \\
\end{array} \nonumber \]

Therefore, the error is \( R_{10} \lt \frac{1}{2(10)^2} = 0.005\).

b. We want to find \( N\) such that \( R_N \lt 0.001\). In part a. we showed that \( R_N \lt 1/2N^2\). Therefore, the remainder \( R_N \lt 0.001\) as long as \( \frac{1}{2N^2} \lt 0.001\). That is, we need \( 2N^2 \gt 1000\). Solving this inequality for \( N\), we see that we need \( N \gt 22.36\). To ensure that the remainder is within the desired amount, we need to round up to the nearest integer. Therefore, the minimum necessary value is \( N=23\).

Exercise \( \PageIndex{4}\)

For \(\displaystyle \sum^ \infty _{n=1}\frac{1}{n^4}\), calculate \( S_5\) and estimate the error \( R_5\).

Hint

Use the remainder estimate \(\displaystyle R_N \lt \int ^ \infty _N\frac{1}{x^4}\,dx.\)

Answer

\( S_5 \approx 1.09035, R_5 \lt 0.00267\)

Subsection Footnotes

⁴ Remember, when dealing with the Integral Test, the terms of your base sequence, \( \{ a_n \} \) must eventually be non-negative.

---

Key Concepts

• If \(\displaystyle \lim_{n \to \infty }a_n \neq 0,\) then the series \(\displaystyle \sum^ \infty _{n=1}a_n\) diverges.
• If \(\displaystyle \lim_{n \to \infty }a_n=0,\) the series \(\displaystyle \sum^ \infty _{n=1}a_n\) may converge or diverge.
• If \(\displaystyle \sum^ \infty _{n=1}a_n\) is a series with positive terms \( a_n\) and \( f\) is a continuous, decreasing function such that \( f(n)=a_n\) for all positive integers \( n\), then

\[\sum_{n=1}^ \infty a_n \nonumber \] and \[ \int ^ \infty _1f(x)\,dx \nonumber \]

either both converge or both diverge. Furthermore, if \(\displaystyle \sum^ \infty _{n=1}a_n\) converges, then the \(N^{\text{th}}\) partial sum approximation \( S_N\) is accurate up to an error \( R_N\) where \(\displaystyle \int ^ \infty _{N+1}f(x)\,dx<R_N< \int ^ \infty _Nf(x)\,dx\).

• The \(p\)-series \(\displaystyle \sum_{n=1}^ \infty \frac{1}{n^p}\) converges if \( p>1\) and diverges if \( p \leq 1.\)

---

Key Equations

• Divergence Test

If \( a_n↛0\) as \(\displaystyle n \to \infty ,\sum_{n=1}^ \infty a_n\) diverges.

• p-series

\(\displaystyle \sum_{n=1}^ \infty \dfrac{1}{n^p}\quad \begin{cases}\text{converges}, \text{if}\;p>1\\\text{diverges}, \text{if}\; p \leq 1\end{cases}\)

• Remainder estimate from the Integral Test

\(\displaystyle \int ^ \infty _{N+1}f(x)\,dx<R_N< \int ^ \infty _Nf(x)\,dx\)

---

Glossary

Divergence Test

if \(\displaystyle \lim_{n \to \infty }a_n \neq 0,\) then the series \(\displaystyle \sum^ \infty _{n=1}a_n\) diverges

Integral Test

for a series \(\displaystyle \sum^ \infty _{n=1}a_n\) with positive terms \( a_n\), if there exists a continuous, decreasing function \( f\) such that \( f(n)=a_n\) for all positive integers \( n\), then

\[\sum_{n=1}^ \infty a_n \nonumber \] and \[ \int ^ \infty _1f(x)\,dx \nonumber \]

either both converge or both diverge

p-series

a series of the form \(\displaystyle \sum^ \infty _{n=1}1/n^p\)

remainder estimate

for a series \(\displaystyle \sum^ \infty _{n=}1a_n\) with positive terms \( a_n\) and a continuous, decreasing function \( f\) such that \( f(n)=a_n\) for all positive integers \( n\), the remainder \(\displaystyle R_N=\sum^ \infty _{n=1}a_n−\sum^N_{n=1}a_n\) satisfies the following estimate:

\[ \int ^ \infty _{N+1}f(x)\,dx<R_N< \int ^ \infty _Nf(x)\,dx \nonumber \]