5.3: Constant Coefficient Homogeneous Equations

This section deals with homogeneous equations of the special form \(ay''+by'+cy=0\), where \(a\), \(b\), and \(c\) are constant (\(a\ne0\)).

If \(a,b\), and \(c\) are real constants and \(a\ne0\), then

\[\label{eq:5.2.1} ay''+by'+cy=0.\]

is said to be a constant coefficient equation.

As we’ll see, all solutions of Equation \ref{eq:5.2.1} are defined on \((-\infty,\infty)\). This being the case, we’ll omit references to the interval on which solutions are defined, or on which a given set of solutions is a fundamental set, etc., since the interval will always be \((-\infty,\infty)\).

To get an idea of what form the solution might be, let's consider the analogous first order equation

\[ay'+by=0.\nonumber\]

This is a simple separable equation whose solution is \[y=e^{{-b\over a}x}\nonumber\]

Since \({-b\over a}\) is just a constant we will replace it with the constant \(r\) and we get a solution of the form \[y=e^{rx}\nonumber\]

Mathematicians, being inherently lazy, figured it's worth trying the same solution in \ref{eq:5.2.1} and see if we can make it work.

Thus, if \(y=e^{rx}\) then \(y'=re^{rx}\) and \(y''=r^2e^{rx}\), so

\[ay''+by'+cy=ar^2e^{rx}+bre^{rx}+ce^{rx}=(ar^2+br+c)e^{rx}=0\nonumber\]

So, solving \ref{eq:5.2.1} is the same thing as solving

\[\label{eq:5.2.2} ar^2+br+c=0.\]

Note: we can ignore \(e^{rx}\) because it is never 0.

\ref{eq:5.2.2} is called the characteristic equation of Equation \ref{eq:5.2.1}.

The roots of the characteristic equation are given by the quadratic formula

\[\label{eq:5.2.3} r={-b\pm\sqrt{b^2-4ac}\over2a}.\]

Three Cases

As you'll recall from algebra, there are three possible types of solutions to \ref{eq:5.2.2} and we will exam each case separately

• Case 1: \(b^2-4ac>0\), so the characteristic equation has two distinct real roots.
• Case 2: \(b^2-4ac=0\), so the characteristic equation has a repeated real root.
• Case 3: \(b^2-4ac<0\), so the characteristic equation has complex roots.

Case 1: Distinct Real Roots

Let \(r_1\) and \(r_2\) be distinct real roots of \ref{eq:5.2.2}.

As such, we get two solutions, \(y_1=e^{r_1x}\) and \(y_2=e^{r_2x}\).

The only question is whether or not these are linearly independent of each other. In this case we'll use the Wronskian.

\[W(x)=\left| \begin{array}{rr} e^{r_1x} & e^{r_2x} \\ r_1e^{r_1x} & r_2e^{r_2x} \end{array} \right|=(r_2-r_1)e^{(r_1+r_2)x}\not\equiv0\nonumber\] for all x since \(r_1\ne r_2\) as the roots are distinct.

So, in this case, the general solution is \[y=c_1e^{r_1x}+c_2e^{r_2x}\]

Example 5.3.1

1. Find the general solution of \[\label{eq:5.2.4} y''+6y'+5y=0.\]
2. Solve the initial value problem \[\label{eq:5.2.5} y''+6y'+5y=0, \quad y(0)=3,\; y'(0)=-1.\]

Solution a

The characteristic equation of Equation \ref{eq:5.2.4} is

\[r^2+6r+5=(r+1)(r+5)=0.\nonumber\]

Since \(r=-1\) and \(r=-5\) are roots, \(y_1=e^{-x}\) and \(y_2=e^{-5x}\) are solutions of Equation \ref{eq:5.2.4} and the general solution of Equation \ref{eq:5.2.4} is

\[\label{eq:5.2.6} y=c_1e^{-x}+c_2e^{-5x}.\]

Solution b

We must determine \(c_1\) and \(c_2\) in Equation \ref{eq:5.2.6} so that \(y\) satisfies the initial conditions in Equation \ref{eq:5.2.5}. Differentiating Equation \ref{eq:5.2.6} yields

\[\label{eq:5.2.7} y'=-c_1e^{-x}-5c_2e^{-5x}.\]

Imposing the initial conditions \(y(0)=3,\, y'(0)=-1\) in Equation \ref{eq:5.2.6} and Equation \ref{eq:5.2.7} yields

\[\begin{array}{rcr} \phantom{-}c_1+\phantom{5}c_2 & = & 3\phantom{.}\\ -c_1-5c_2 & = & -1. \end{array}\nonumber \]

The solution of this system is \(c_1=7/2,c_2=-1/2\). Therefore the solution of Equation \ref{eq:5.2.5} is

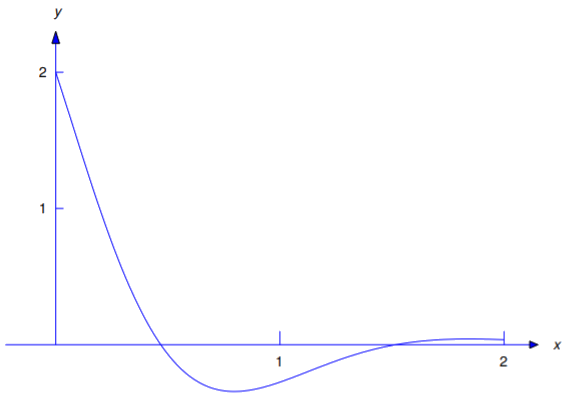
\[y={7\over2}e^{-x}-{1\over2}e^{-5x}.\nonumber \]

Figure 5.3.1 is a graph of this solution.

Figure 5.3.1 : \(y=\frac{7}{2}e^{-x}-\frac{1}{2}e^{-5x}\)

Case 2: A Repeated Real Root

Let \(r\) be a repeated real root of \ref{eq:5.2.2}. As such, we only get one solution, \(y_1=e^{rx}\). But we know there must be two independent solutions to a second order homogeneous differential equation. So, how can we find a second independent solution if we only know one? Recall the formula for a second solution that we derived in section 5.2,

\[y_2=y_1\int{e^{-\int{p(x)dx}}\over y_1^2}dx\nonumber\]

If we divide \ref{eq:5.2.1} by \(a\) we get \[y''+{b\over a}y'+{c\over a}y=0\nonumber\]

which gives is \(p(x)={b\over a}\), which gives us \[y_2=e^{rx}\int{e^{-\int{b\over a}dx}\over e^{2rx}}dx\nonumber\]

\[=e^{rx}\int{e^{-{b\over a}x}\over e^{2rx}}dx\nonumber\]

Since we have a repeated root we know \(b^2-4ac=0\) in \ref{eq:5.2.3} which gives us \(r={-b\over 2a}\) or

\[{-b\over a}=2r\nonumber\]

Using this we now get \[y_2=e^{rx}\int{e^{2rx}\over e^{2rx}}dx\nonumber\]

\[=e^{rx}\int dx\nonumber\]

\[=xe^{rx}\nonumber\]

Since we already know that the formula gives us a second linearly independent solution, the general solution is \[y=c_1e^{rx}+c_2xe^{rx}\]

Example 5.3.2

1. Find the general solution of \[\label{eq:5.2.8} y''+6y'+9y=0.\]
2. Solve the initial value problem \[\label{eq:5.2.9} y''+6y'+9y=0, \quad y(0)=3,\; y'(0)=-1.\]

Solution a

The characteristic equation of Equation \ref{eq:5.2.8} is

\[r^2+6r+9=(r+3)^2=0,\nonumber \]

so the characteristic equation has the repeated real root \(r=-3\). Therefore \(y_1=e^{-3x}\) and \(y_2=xe^{-3x}\) are linearly independent solutions of Equation \ref{eq:5.2.8} and the general solution of Equation \ref{eq:5.2.8} is

\[\label{eq:5.2.10} y=c_1e^{-3x}+c_2xe^{-3x}.\]

Solution b

b. Differentiating Equation \ref{eq:5.2.10} yields

\[\label{eq:5.2.11} y'=-3e^{-3x}(c_1+c_2x)+c_2e^{-3x}.\]

Imposing the initial conditions \(y(0)=3,\, y'(0)=-1\) in Equation \ref{eq:5.2.10} and Equation \ref{eq:5.2.11} yields \(c_1=3\) and \(-3c_1+c_2=-1\), so \(c_2=8\). Therefore the solution of Equation \ref{eq:5.2.9} is

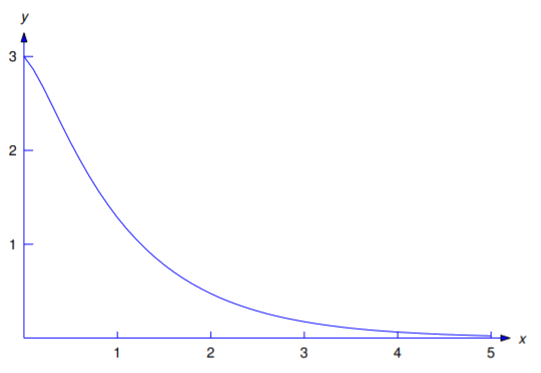
\[y=3e^{-3x}+8xe^{-3x}.\nonumber \]

Figure 5.3.2 is a graph of this solution.

Figure 5.3.2 : \(y=3e^{-3x}+8xe^{-3x}\)

Case 3: Complex Conjugate Roots

Now suppose \ref{eq:5.2.2} has complex conjugate roots \(r=\lambda \pm \omega i\). This is similar to case one in that we do have distinct roots and we could say \(y_1=e^{(\lambda + \omega i)x}\) and \(y_2=e^{(\lambda - \omega i)x}\). The problem with this is that it's not very useful in real life applications to have functions of complex numbers. So, we want to see if we can somehow write both solutions as functions of real numbers, and the following theorem gives us exactly what we need.

Theorem \(\PageIndex{1}\) Euler's Identity

\[e^{i \theta}=\cos \theta+i\sin \theta\]

Proof

See Exercise 23.

We can now rewrite \(y_1\) and \(y_2\) as follows:

\[y_1=e^{(\lambda + \omega i)x}=e^{\lambda x}e^{i\omega x}=e^{\lambda x}(\cos \omega x+i\sin \omega x)=e^{\lambda x}\cos \omega x+ie^{\lambda x}\sin \omega x)\nonumber\]

and

\[y_2=e^{(\lambda - \omega i)x}=e^{\lambda x}e^{-i\omega x}=e^{\lambda x}(\cos (-\omega x)+i\sin (-\omega x))=e^{\lambda x}\cos \omega x-ie^{\lambda x}\sin \omega x)\nonumber\]

The latter is using the fact the \(\cos\) is an even function and \(\sin\) is an odd function.

Note: the \(i\) is no longer inside a function.

Recall that if \(y_1\) and \(y_2\) are solutions of a homogeneous equation, then any linear combination is also a solution. So, if we add \(y_1\) and \(y_2\) we get

\[y_3=2e^{\lambda x}\cos \omega x\nonumber\]

and if we subtract \(y_1\) and \(y_2\) we get

\[y_4=2ie^{\lambda x}\sin \omega x\nonumber\]

Now, both 2 and 2i are constants that can be absorbed into the constants \(c_1\) and \(c_2\) of our general solution and since \(y_3\) and \(y_4\) are not constant multiples of each other, they are independent. Thus, our general solution is \[y=c_1e^{\lambda x}\cos \omega x+c_2e^{\lambda x}\sin \omega x\]

Example 5.3.3

1. Find the general solution of \[\label{eq:5.2.14} y''+4y'+13y=0.\]
2. Solve the initial value problem \[\label{eq:5.2.15} y''+4y'+13y=0, \quad y(0)=2,\; y'(0)=-3.\]

Solution a

The characteristic equation of Equation \ref{eq:5.2.14} is

\[r^2+4r+13=r^2+4r+4+9=(r+2)^2+9=0.\nonumber \]

The roots of the characteristic equation are \(r=-2 \pm 3i\) and the general solution of \ref{eq:5.2.14} is

\[y=c_1e^{-2x}\cos 3x+c_2e^{-2x}\sin 3x\nonumber\]

Solution b

Imposing the condition \(y(0)=2\) in Equation \ref{eq:5.2.14} shows that \(c_1=2\). Differentiating Equation \ref{eq:5.2.14} yields

\[y'=-2e^{-2x}(c_1\cos 3x+c_2\sin 3x) +3e^{-2x}(-c_1\sin 3x +c_2\cos 3x),\nonumber \]

and imposing the initial condition \(y'(0)=-3\) here yields \(-3=-2c_1+3c_2\), so \(c_2=1/3\). Therefore the solution of Equation \ref{eq:5.2.15} is

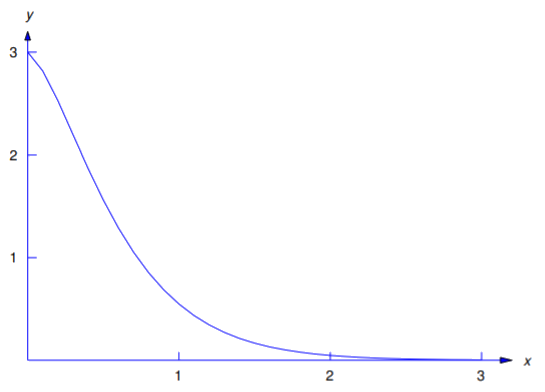
\[y=2e^{-2x}\cos 3x+ {1\over3}e^{-2x}\sin 3x.\nonumber \]

Figure 5.3.3 is a graph of this function.

Figure 5.3.3 : \(y=2e^{-2x}\cos 3x+ {1\over3}e^{-2x}\sin 3x\)