5.6: Divide Monomials
- Page ID
- 79471
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Simplify expressions using the Quotient Property for Exponents
- Simplify expressions with zero exponents
- Simplify expressions using the quotient to a Power Property
- Simplify expressions by applying several properties
- Divide monomials
Note
Before you get started, take this readiness quiz.
- Simplify: \(\dfrac{8}{24}\).
If you missed this problem, review Exercise 1.6.4. - Simplify: \((2m^3)^5\).
If you missed this problem, review Exercise 6.2.22. - Simplify: \(\dfrac{12x}{12y}\)
If you missed this problem, review Exercise 1.6.10.
Simplify Expressions Using the Quotient Property for Exponents
Earlier in this chapter, we developed the properties of exponents for multiplication. We summarize these properties below.
SUMMARY OF EXPONENT PROPERTIES FOR MULTIPLICATION
If a and b are real numbers, and m and n are whole numbers, then
\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]
Now we will look at the exponent properties for division. A quick memory refresher may help before we get started. You have learned to simplify fractions by dividing out common factors from the numerator and denominator using the Equivalent Fractions Property. This property will also help you work with algebraic fractions—which are also quotients.
EQUIVALENT FRACTIONS PROPERTY
If a, b, and c are whole numbers where \(b\neq 0,c\neq 0\).
\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]
As before, we’ll try to discover a property by looking at some examples.
\(\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\)
Notice, in each case the bases were the same and we subtracted exponents.
When the larger exponent was in the numerator, we were left with factors in the numerator.
When the larger exponent was in the denominator, we were left with factors in the denominator—notice the numerator of 1.
We write:
\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3}-2}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]
This leads to the Quotient Property for Exponents.
QUOTIENT PROPERTY FOR EXPONENTS
If a is a real number, \(a\neq 0\), and m and n are whole numbers, then
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
A couple of examples with numbers may help to verify this property.
\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]
Exercise \(\PageIndex{1}\)
Simplify:
- \(\dfrac{x^{9}}{x^{7}}\)
- \(\dfrac{3^{10}}{3^{2}}\)
- Answer
-
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
1.
Since 9 > 7, there are more factors of x in the numerator. 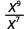
Use the Quotient Property, \(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 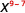
Simplify. 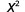
2.
Notice that when the larger exponent is in the numerator, we are left with factors in the numerator.Since 10 > 2, there are more factors of x in the numerator. 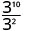
Use the Quotient Property, \(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 
Simplify. 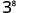
Exercise \(\PageIndex{2}\)
Simplify:
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^{5}}\)
- Answer
-
- \(x^{5}\)
- \(6^9\)
Exercise \(\PageIndex{3}\)
Simplify:
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- Answer
-
- \(y^{6}\)
- \(10^8\)
Exercise \(\PageIndex{4}\)
Simplify:
- \(\dfrac{b^{8}}{b^{12}}\)
- \(\dfrac{7^{3}}{7^{5}}\)
- Answer
-
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
1.
Since 12 > 8, there are more factors of b in the denominator. 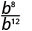
Use the Quotient Property, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 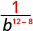
Simplify. 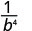
2.
Notice that when the larger exponent is in the denominator, we are left with factors in the denominator.Since 5 > 3, there are more factors of 3 in the denominator. 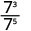
Use the Quotient Property, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 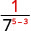
Simplify. 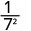
Simplify. 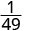
Exercise \(\PageIndex{5}\)
Simplify:
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\)
- Answer
-
- \(\dfrac{1}{x^{4}}\)
- \(\dfrac{1}{12^{15}}\)
Exercise \(\PageIndex{6}\)
Simplify:
- \(\dfrac{m^{7}}{m^{15}}\)
- \(\dfrac{9^{8}}{9^{19}}\)
- Answer
-
- \(\dfrac{1}{m^{8}}\)
- \(\dfrac{1}{9^{11}}\)
Notice the difference in the two previous examples:
- If we start with more factors in the numerator, we will end up with factors in the numerator.
- If we start with more factors in the denominator, we will end up with factors in the denominator.
The first step in simplifying an expression using the Quotient Property for Exponents is to determine whether the exponent is larger in the numerator or the denominator.
Exercise \(\PageIndex{7}\)
Simplify:
- \(\dfrac{a^{5}}{a^{9}}\)
- \(\dfrac{x^{11}}{x^{7}}\)
- Answer
-
1. Is the exponent of a larger in the numerator or denominator? Since 9 > 5, there are more a's in the denominator and so we will end up with factors in the denominator.
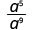
Use the Quotient Property, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 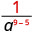
Simplify. 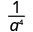
2. Notice there are more factors of xx in the numerator, since 11 > 7. So we will end up with factors in the numerator.
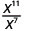
Use the Quotient Property, \(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 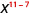
Simplify. 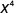
Exercise \(\PageIndex{8}\)
Simplify:
- \(\dfrac{b^{19}}{b^{11}}\)
- \(\dfrac{z^{5}}{z^{11}}\)
- Answer
-
- \(b^{8}\)
- \(\dfrac{1}{z^{6}}\)
Exercise \(\PageIndex{9}\)
Simplify:
- \(\dfrac{p^{9}}{p^{17}}\)
- \(\dfrac{w^{13}}{w^{9}}\)
- Answer
-
- \(\dfrac{1}{p^{8}}\)
- \(w^{4}\)
Simplify Expressions with an Exponent of Zero
A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like \(\dfrac{a^{m}}{a^{m}}\). From your earlier work with fractions, you know that:
\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]
In words, a number divided by itself is 1. So, \(\dfrac{x}{x}=1\), for any \(x(x\neq 0)\), since any number divided by itself is 1.
The Quotient Property for Exponents shows us how to simplify \(\dfrac{a^{m}}{a^{n}}\) when \(m>n\) and when \(n<m\) by subtracting exponents. What if \(m=n\)?
Consider \(\dfrac{8}{8}\), which we know is 1.
\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)
Now we will simplify \(\dfrac{a^{m}}{a^{m}}\) in two ways to lead us to the definition of the zero exponent. In general, for \(a\neq 0\):
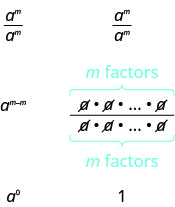
We see \(\dfrac{a^{m}}{a^{m}}\) simplifies to \(a^{0}\) and to 1. So \(a^{0} = 1\).
ZERO EXPONENT
If a is a non-zero number, then \(a^{0} = 1\).
Any nonzero number raised to the zero power is 1.
In this text, we assume any variable that we raise to the zero power is not zero.
Exercise \(\PageIndex{10}\)
Simplify:
- \(9^{0}\)
- \(n^{0}\)
- Answer
-
The definition says any non-zero number raised to the zero power is 1.
- \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
- \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
Exercise \(\PageIndex{11}\)
Simplify:
- \(15^{0}\)
- \(m^{0}\)
- Answer
-
- 1
- 1
Exercise \(\PageIndex{12}\)
Simplify:
- \(k^{0}\)
- \(29^{0}\)
- Answer
-
- 1
- 1
Now that we have defined the zero exponent, we can expand all the Properties of Exponents to include whole number exponents.
What about raising an expression to the zero power? Let’s look at \((2x)^0\). We can use the product to a power rule to rewrite this expression.
\(\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\)
This tells us that any nonzero expression raised to the zero power is one.
Exercise \(\PageIndex{13}\)
Simplify:
- \((5b)^0\)
- \((−4a^{2}b)^0\).
- Answer
-
- \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
- \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
Exercise \(\PageIndex{14}\)
Simplify:
- \((11z)^0\)
- \((−11pq^{3})^0\).
- Answer
-
- 1
- 1
Exercise \(\PageIndex{15}\)
Simplify:
- \((-6d)^0\)
- \((−8m^{2}n^{3})^0\).
- Answer
-
- 1
- 1
Simplify Expressions Using the Quotient to a Power Property
Now we will look at an example that will lead us to the Quotient to a Power Property.
\(\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\)
Notice that the exponent applies to both the numerator and the denominator.
\(\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\)
This leads to the Quotient to a Power Property for Exponents.
QUOTIENT TO A POWER PROPERTY FOR EXPONENTS
If a and b are real numbers, \(b\neq 0\), and m is a counting number, then
\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]
To raise a fraction to a power, raise the numerator and denominator to that power.
An example with numbers may help you understand this property:
\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]
Exercise \(\PageIndex{16}\)
Simplify:
- \(\left(\dfrac{3}{7}\right)^{2}\)
- \(\left(\dfrac{b}{3}\right)^{4}\)
- \(\left(\dfrac{k}{j}\right)^{3}\)
- Answer
-
1.
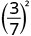
Use the Quotient Property, \(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 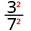
Simplify. 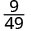
2.
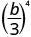
Use the Quotient Property, \(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 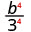
Simplify. 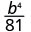
3.
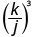
Raise the numerator and denominator to the third power. 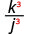
Exercise \(\PageIndex{17}\)
Simplify:
- \(\left(\dfrac{5}{8}\right)^{2}\)
- \(\left(\dfrac{p}{10}\right)^{4}\)
- \(\left(\dfrac{m}{n}\right)^{7}\)
- Answer
-
- \(\dfrac{25}{64}\)
- \(\dfrac{p^{4}}{10,000}\)
- \(\dfrac{m^{7}}{n^{7}}\)
Exercise \(\PageIndex{18}\)
Simplify:
- \(\left(\dfrac{1}{3}\right)^{3}\)
- \(\left(\dfrac{-2}{q}\right)^{3}\)
- \(\left(\dfrac{w}{x}\right)^{4}\)
- Answer
-
- \(\dfrac{1}{27}\)
- \(\dfrac{-8}{q^{3}}\)
- \(\dfrac{w^{4}}{x^{4}}\)
Simplify Expressions by Applying Several Properties
We’ll now summarize all the properties of exponents so they are all together to refer to as we simplify expressions using several properties. Notice that they are now defined for whole number exponents.
SUMMARY OF EXPONENT PROPERTIES
If a and b are real numbers, and m and n are whole numbers, then
\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]
Exercise \(\PageIndex{19}\)
Simplify: \(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)
- Answer
-
\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)
Exercise \(\PageIndex{20}\)
Simplify: \(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)
- Answer
-
\(m^{13}\)
Exercise \(\PageIndex{21}\)
Simplify: \(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)
- Answer
-
\(k^{5}\)
Exercise \(\PageIndex{22}\)
Simplify: \(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)
- Answer
-
\(\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\)
Notice that after we simplified the denominator in the first step, the numerator and the denominator were equal. So the final value is equal to 1.
Exercise \(\PageIndex{23}\)
Simplify:\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\)
- Answer
-
1
Exercise \(\PageIndex{24}\)
Simplify:\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\)
- Answer
-
1
Exercise \(\PageIndex{25}\)
Simplify: \(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)
- Answer
-
\(\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\)
Exercise \(\PageIndex{25}\)
Simplify: \(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)
- Answer
-
\(r^{8}\)
Exercise \(\PageIndex{25}\)
Simplify: \(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)
- Answer
-
\(v^{6}\)
Exercise \(\PageIndex{26}\)
Simplify:\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)
- Answer
-
Here we cannot simplify inside the parentheses first, since the bases are not the same.
\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)
Exercise \(\PageIndex{27}\)
Simplify:\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)
- Answer
-
\(\dfrac{a^{12}}{b^{8}}\)
Exercise \(\PageIndex{28}\)
Simplify: \(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)
- Answer
-
\(\dfrac{q^{21}}{r^{15}}\)
Exercise \(\PageIndex{29}\)
Simplify:\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)
- Answer
-
\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)
Exercise \(\PageIndex{30}\)
Simplify:\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)
- Answer
-
\(\dfrac{49 x^{6}}{81 y^{2}}\)
Exercise \(\PageIndex{31}\)
Simplify: \(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)
- Answer
-
\(\dfrac{9 x^{8}}{49 v^{2}}\)
Exercise \(\PageIndex{32}\)
Simplify: \(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)
- Answer
-
\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)
Exercise \(\PageIndex{32}\)
Simplify: \(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)
- Answer
-
\(\dfrac{1}{a^{6}}\)
Exercise \(\PageIndex{33}\)
Simplify: \(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)
- Answer
-
\(\dfrac{1}{p^{15}}\)
Exercise \(\PageIndex{34}\)
Simplify:\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)
- Answer
-
\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)
Exercise \(\PageIndex{35}\)
Simplify: \(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)
- Answer
-
9\(r^{18}\)
Exercise \(\PageIndex{36}\)
Simplify: \(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)
- Answer
-
\(\dfrac{2}{x}\)
Divide Monomials
You have now been introduced to all the properties of exponents and used them to simplify expressions. Next, you’ll see how to use these properties to divide monomials. Later, you’ll use them to divide polynomials.
Exercise \(\PageIndex{37}\)
Find the quotient: \(56 x^{7} \div 8 x^{3}\)
- Answer
-
\(\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\)
Exercise \(\PageIndex{38}\)
Find the quotient:42\(y^{9} \div 6 y^{3}\)
- Answer
-
\(7y^{6}\)
Exercise \(\PageIndex{39}\)
Find the quotient:\(48z^{8} \div 8 z^{2}\)
- Answer
-
\(6z^{6}\)
Exercise \(\PageIndex{40}\)
Find the quotient: \(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)
- Answer
-
When we divide monomials with more than one variable, we write one fraction for each variable.
\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)
Exercise \(\PageIndex{41}\)
Find the quotient: \(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)
- Answer
-
\(-\dfrac{9}{a^{5} b}\)
Exercise \(\PageIndex{42}\)
Find the quotient: \(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)
- Answer
-
\(\dfrac{-9 d}{c^{4}}\)
Exercise \(\PageIndex{43}\)
Find the quotient: \(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)
- Answer
-
\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)
Exercise \(\PageIndex{44}\)
Find the quotient: \(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)
- Answer
-
\(\dfrac{2 a^{6}}{3 b^{2}}\)
Exercise \(\PageIndex{45}\)
Find the quotient: \(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)
- Answer
-
\(-\dfrac{3 q^{6}}{5 p^{8}}\)
Once you become familiar with the process and have practiced it step by step several times, you may be able to simplify a fraction in one step.
Exercise \(\PageIndex{46}\)
Find the quotient: \(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)
- Answer
-
Be very careful to simplify \(\dfrac{14}{21}\) by dividing out a common factor, and to simplify the variables by subtracting their exponents.
\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)
Exercise \(\PageIndex{47}\)
Find the quotient:\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)
- Answer
-
\(\dfrac{4 y^{2}}{7 x^{4}}\)
Exercise \(\PageIndex{48}\)
Find the quotient:\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)
- Answer
-
\(\dfrac{5}{8 m^{5} n^{3}}\)
In all examples so far, there was no work to do in the numerator or denominator before simplifying the fraction. In the next example, we’ll first find the product of two monomials in the numerator before we simplify the fraction. This follows the order of operations. Remember, a fraction bar is a grouping symbol.
Exercise \(\PageIndex{49}\)
Find the quotient: \(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)
- Answer
-
\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)
Exercise \(\PageIndex{50}\)
Find the quotient: \(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)
- Answer
-
\(2 a b^{2}\)
Exercise \(\PageIndex{51}\)
Find the quotient:\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)
- Answer
-
\(-4 x y^{5}\)
Note
Access these online resources for additional instruction and practice with dividing monomials:
Key Concepts
- Quotient Property for Exponents:
- If a is a real number, \(a\neq 0\), and m,n are whole numbers, then: \(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
- Zero Exponent
- If a is a non-zero number, then \(a^{0} =1\).
- Quotient to a Power Property for Exponents:
- If a and b are real numbers, \(b\neq 0\), and mm is a counting number, then: \(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
- To raise a fraction to a power, raise the numerator and denominator to that power.
- Summary of Exponent Properties
- If a,b are real numbers and m,nm,n are whole numbers, then \(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)


