7.2: Multiply and Divide Rational Expressions
- Last updated
- Jul 25, 2021
- Save as PDF
- Page ID
- 79495
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Multiply rational expressions
- Divide rational expressions
Note
Before you get started, take this readiness quiz.
If you miss a problem, go back to the section listed and review the material.
- Multiply: 1415·635.
If you missed this problem, review Exercise 1.6.13. - Divide: 1415÷635.
If you missed this problem, review Exercise 1.6.22. - Factor completely: 2x2−98.
If you missed this problem, review Exercise 7.5.10. - Factor completely: 10n3+10.
If you missed this problem, review Exercise 7.5.19. - Factor completely: 10p2−25pq−15q2.
If you missed this problem, review Exercise 7.5.28.
Multiply Rational Expressions
To multiply rational expressions, we do just what we did with numerical fractions. We multiply the numerators and multiply the denominators. Then, if there are any common factors, we remove them to simplify the result.
Definition: MULTIPLICATION OF RATIONAL EXPRESSIONS
If p,q,r,s are polynomials where q≠0 and s≠0
pq·rs=prqsTo multiply rational expressions, multiply the numerators and multiply the denominators.
We’ll do the first example with numerical fractions to remind us of how we multiplied fractions without variables.
Example 7.2.1
Multiply: 1028·815.
- Answer
-
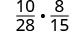
Multiply the numerators and denominators. 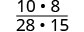
Look for common factors, and then remove them. 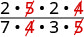
Simplify. 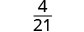
Example 7.2.2
Mulitply: 610·1512.
- Answer
-
34
Example 7.2.3
Mulitply: 2015·68.
- Answer
-
1
Remember, throughout this chapter, we will assume that all numerical values that would make the denominator be zero are excluded. We will not write the restrictions for each rational expression, but keep in mind that the denominator can never be zero. So in this next example, x≠0 and y≠0.
Example 7.2.4
Mulitply: 2x3y2·6xy3x2y.
- Answer
-
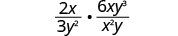
Multiply. 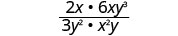
Factor the numerator and denominator completely, and then remove common factors. 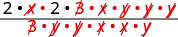
Simplify. 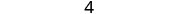
Example 7.2.5
Mulitply: 3pqq2·5p2q6pq.
- Answer
-
5p22q
Example 7.2.6
Mulitply: 6x3y7x2·2xy3x2y.
- Answer
-
12y37
How to Multiply Rational Expressions
Example 7.2.7
Mulitply: 2xx2−7x+12·x2−96x2.
- Answer
-
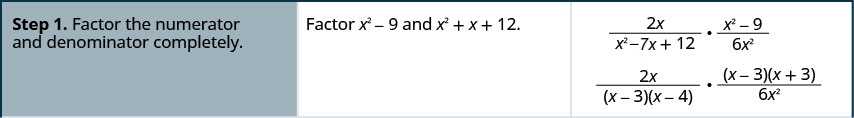


Example 7.2.8
Mulitply: 5xx2+5x+6·x2−410x.
- Answer
-
x−22(x+3)
Example 7.2.9
Mulitply: 9x2x2+11x+30·x2−363x2.
- Answer
-
3(x−6)x+5
Definition: MULTIPLY A RATIONAL EXPRESSION.
- Factor each numerator and denominator completely.
- Multiply the numerators and denominators.
- Simplify by dividing out common factors.
Example 7.2.10
Multiply: n2−7nn2+2n+1·n+12n.
- Answer
-
n2−7nn2+2n+1·n+12n Factor each numerator and denominator. n(n−7)(n+1)(n+1)·n+12n Multiply the numerators and the denominators. n(n−7)(n+1)(n+1)(n+1)2n Simplify. n−72(n+1)
Example 7.2.11
Multiply: x2−25x2−3x−10·x+2x.
- Answer
-
x+5x
Example 7.2.12
Multiply: x2−4xx2+5x+6·x+2x.
- Answer
-
x−4x+3
Example 7.2.13
Multiply: 16−4x2x−12·x2−5x−6x2−16.
- Answer
-
16−4x2x−12·x2−5x−6x2−16 Factor each numerator and denominator. 4(4−x)2(x−6)·(x−6)(x+1)(x−4)(x+4) Multiply the numerators and the denominators. 4(4−x)(x−6)(x+1)2(x−6)(x−4)(x+4) Simplify. −2(x+1)(x+4)
Example 7.2.14
Multiply: 12x−6x2x2+8x·x2+11x+24x2−4.
- Answer
-
−6(x+3)x+2
Example 7.2.15
Multiply: 9v−3v29v+36·v2+7v+12v2−9.
- Answer
-
−v3
Example 7.2.16
Multiply: 2x−6x2−8x+15·x2−252x+10.
- Answer
-
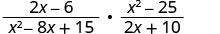
Factor each numerator and denominator. 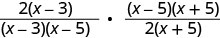
Multiply the numerators and denominators. 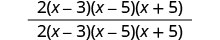
Remove common factors. 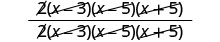
Simplify. 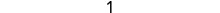
Example 7.2.17
Multiply: 3a−21a2−9a+14·a2−43a+6.
- Answer
-
1
Example 7.2.18
Multiply: b2−bb2+9b−10·b2−100b2−10b.
- Answer
-
1
Divide Rational Expressions
To divide rational expressions we multiply the first fraction by the reciprocal of the second, just like we did for numerical fractions.
Remember, the reciprocal of ab is ba. To find the reciprocal we simply put the numerator in the denominator and the denominator in the numerator. We “flip” the fraction.
Definition: DIVISION OF RATIONAL EXPRESSIONS
If p,q,r,s are polynomials where q≠0, r≠0, s≠0
pq÷rs=pq·sr
To divide rational expressions multiply the first fraction by the reciprocal of the second.
How to Divide Rational Expressions
Example 7.2.19
Divide: x+96−x÷x2−81x−6.
- Answer
-




Example 7.2.20
Divide: c+35−c÷c2−9c−5.
- Answer
-
−1c−3
Example 7.2.21
Divide: 2−dd−4÷4−d24−d.
- Answer
-
−12+d
Definition: DIVIDE RATIONAL EXPRESSIONS.
- Rewrite the division as the product of the first rational expression and the reciprocal of the second.
- Factor the numerators and denominators completely.
- Multiply the numerators and denominators together.
- Simplify by dividing out common factors.
Example 7.2.22
Divide: 3n2n2−4n÷9n2−45nn2−7n+10.
- Answer
-
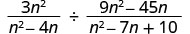
Rewrite the division as the product of the first rational expression and the reciprocal of the second. 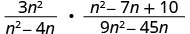
Factor the numerators and denominators and then multiply. 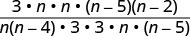
Simplify by dividing out common factors. 
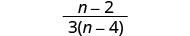
Example 7.2.23
Divide: 2m2m2−8m÷8m2+24mm2+m−6.
- Answer
-
(m−2)4(m−8)
Example 7.2.24
Divide: 15n23n2+33n÷5n−5n2+9n−22.
- Answer
-
n(n−2)n−1
Remember, first rewrite the division as multiplication of the first expression by the reciprocal of the second. Then factor everything and look for common factors.
Example 7.2.25
Divide: 2x2+5x−12x2−16÷2x2−13x+15x2−8x+16.
- Answer
-
2x2+5x−12x2−16÷2x2−13x+15x2−8x+16 Rewrite the division as the product of the first rational expression and the reciprocal of the second. 2x2+5x−12x2−16·x2−8x+162x2−13x+15 Factor the numerators and denominators and then multiply. (2x−3)(x+4)(x−4)(x−4)(x−4)(x+4)(2x−3)(x−5) Simplify. (x−4)(x−5)
Example 7.2.26
Divide: 3a2−8a−3a2−25÷3a2−14a−5a2+10a+25.
- Answer
-
(a−3)(a+5)(a−5)(a−5)
Exercise 7.2.27
Divide: 4b2+7b−21−b2÷4b2+15b−4b2−2b+1.
- Answer
-
−(b+2)(b−1)(1+b)(b+4)
Example 7.2.28
Divide: p3+q32p2+2pq+2q2÷p2−q26.
- Answer
-
p3+q32p2+2pq+2q2÷p2−q26 Rewrite the division as the product of the first rational expression and the reciprocal of the second. p3+q32p2+2pq+2q2·6p2−q2 Factor the numerators and denominators and then multiply. (p+q)(p2−pq+q2)62(p2+pq+q2)(p−q)(p+q) Simplify. 3(p2−pq+q2)(p−q)(p2+pq+q2)
Example 7.2.29
Divide: x3−83x2−6x+12÷x2−46.
- Answer
-
2(x2+2x+4)(x+2)(x2−2x+4)
Example 7.2.30
Divide: 2z2z2−1÷z3−z2+zz3−1.
- Answer
-
2z(z2+z+1)(z+1)(z2−z+1)
Before doing the next example, let’s look at how we divide a fraction by a whole number. When we divide 35÷4
35÷435÷4135·14
We do the same thing when we divide rational expressions.
Example 7.2.31
a2−b23ab÷(a2+2ab+b2).
- Answer
-
a2−b23ab÷(a2+2ab+b2) Write the second expression as a fraction. a2−b23ab÷a2+2ab+b21 Rewrite the division as the first expression times the reciprocal of the second expression. a2−b23ab·1a2+2ab+b2 Factor the numerators and the denominators, and then multiply. (a−b)(a+b)13ab·(a+b)(a+b) Simplify. a−b3ab(a+b)
Example 7.2.32
2x2−14x−164÷(x2+2x+1).
- Answer
-
x−82(x+1)
Example 7.2.33
y2−6y+8y2−4y÷(3y2−12y).
- Answer
-
y−23y(y−4)
Example 7.2.34
6x2−7x+24x−82x2−7x+3x2−5x+6.
- Answer
-
6x2−7x+24x−82x2−7x+3x2−5x+6 Rewrite with a division sign. 6x2−7x+24x−8÷2x2−7x+3x2−5x+6 Rewrite as product of first times reciprocal of second. 6x2−7x+24x−8·x2−5x+62x2−7x+3 Factor the numerators and the denominators, and then multiply (2x−1)(3x−2)(x−2)(x−3)4(x−2)(2x−1)(x−3) Simplify. 3x−24
Example 7.2.35
3x2+7x+24x+243x2−14x−5x2+x−30.
- Answer
-
x+24
Example 7.2.36
y2−362y2+11y−62y2−2y−608y−4.
- Answer
-
2y+5
If we have more than two rational expressions to work with, we still follow the same procedure. The first step will be to rewrite any division as multiplication by the reciprocal. Then we factor and multiply.
Example 7.2.37
3x−64x−4·x2+2x−3x2−3x−10÷2x+128x+16.
- Answer
-
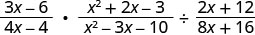
Rewrite the division as multiplication by the reciprocal. 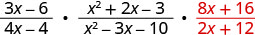
Factor the numerators and the denominators, and then multiply. 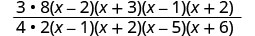
Simplify by dividing out common factors. 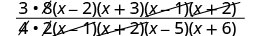
Simplify. 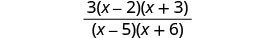
Example 7.2.38
4m+43m−15·m2−3m−10m2−4m−32÷12m−366m−48.
- Answer
-
2(m+1)(m+2)3(m+4)(m−3)
Example 7.2.39
2n2+10nn−1÷n2+10n+24n2+8n−9·n+48n2+12n.
- Answer
-
(n+5)(n+9)2(n+6)(2n+3)
Key Concepts
- Multiplication of Rational Expressions
- If p,q,r,s are polynomials where q≠0 and s≠0, then pq·rs=prqs
- To multiply rational expressions, multiply the numerators and multiply the denominators
- Multiply a Rational Expression
- Factor each numerator and denominator completely.
- Multiply the numerators and denominators.
- Simplify by dividing out common factors.
- Division of Rational Expressions
- If p,q,r,s are polynomials where q≠0, r≠0, s≠0, then pq÷rs=pq·sr
- To divide rational expressions multiply the first fraction by the reciprocal of the second.
- Divide Rational Expressions
- Rewrite the division as the product of the first rational expression and the reciprocal of the second.
- Factor the numerators and denominators completely.
- Multiply the numerators and denominators together.
- Simplify by dividing out common factors.


