8.5: Solving Nonlinear Systems

Learning Objectives

• Identify nonlinear systems.
• Solve nonlinear systems using the substitution method.

Nonlinear Systems

A system of equations where at least one equation is not linear is called a nonlinear system³². In this section we will use the substitution method to solve nonlinear systems. Recall that solutions to a system with two variables are ordered pairs \((x,y)\) that satisfy both equations.

Example \(\PageIndex{1}\):

Solve: \(\left\{\begin{array}{l}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\right.\).

Solution

In this case we begin by solving for x in the first equation.

\(\left\{\begin{array}{c}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\Longrightarrow x=-2y \right.\)

Substitute \(x=−2y\) into the second equation and then solve for \(y\).

\(\begin{aligned}(\color{Cerulean}{-2y }\color{black}{)}^{2}+y^{2} &=5 \\ 4 y^{2}+y^{2} &=5 \\ 5 y^{2} &=5 \\ y^{2} &=1 \\ y &=\pm 1 \end{aligned}\)

Here there are two answers for \(y\); use \(x=−2y\) to find the corresponding \(x\)-values.

Table \(\PageIndex{1}\)

Using \(y=-1\)	Using \(y=1\)
\(\begin{aligned} x &=-2 y \\ &=-2(-1) \\ &=2 \end{aligned}\)	\(\begin{aligned} x &=-2 y \\ &=-2(1) \\ &=-2 \end{aligned}\)

This gives us two ordered pair solutions, \((2,−1)\) and \((−2,1)\).

Answer:

\((2,−1), (−2,1)\)

In the previous example, the given system consisted of a line and a circle. Graphing these equations on the same set of axes, we can see that the two ordered pair solutions correspond to the two points of intersection.

Figure \(\PageIndex{1}\)

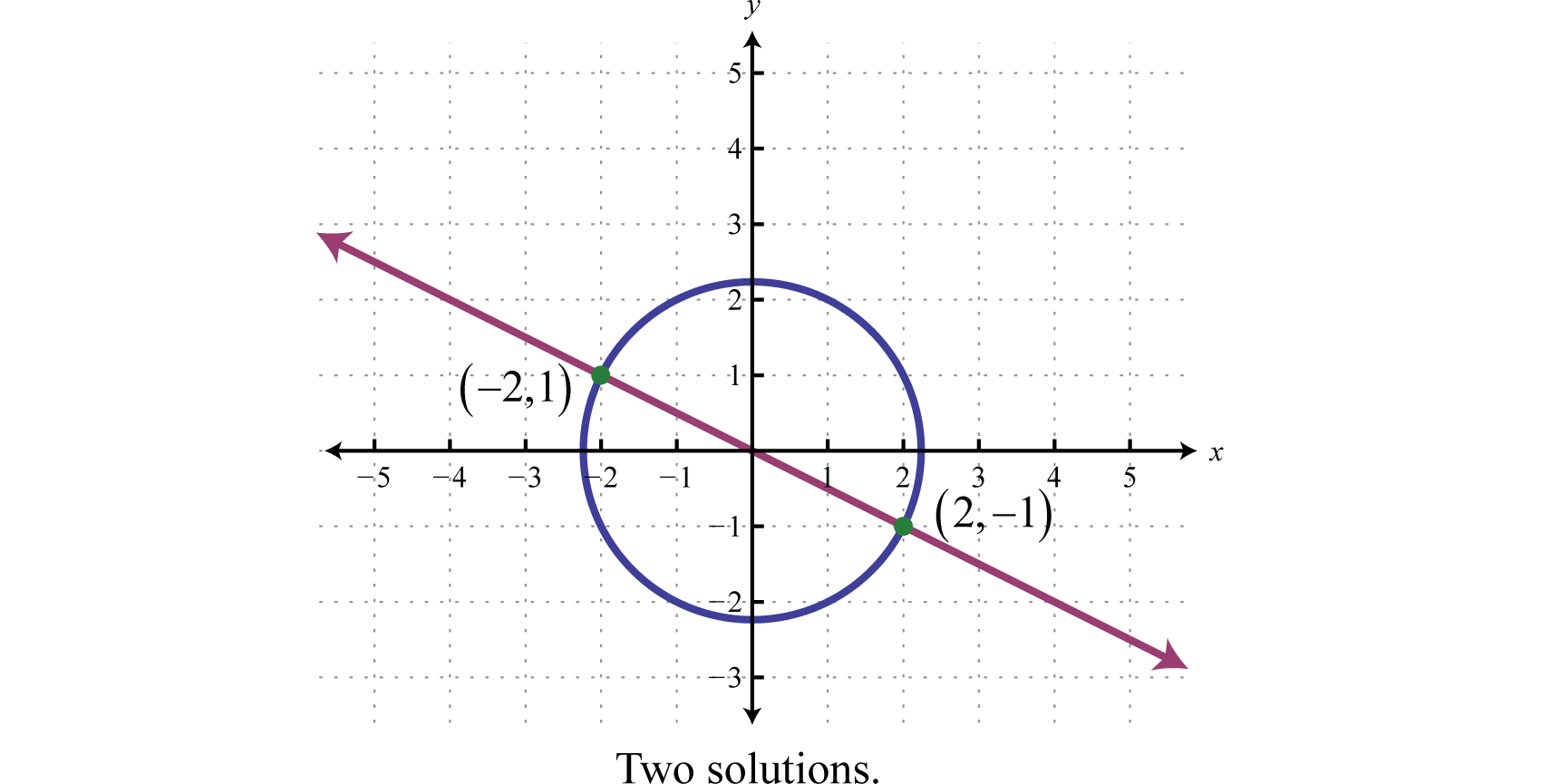
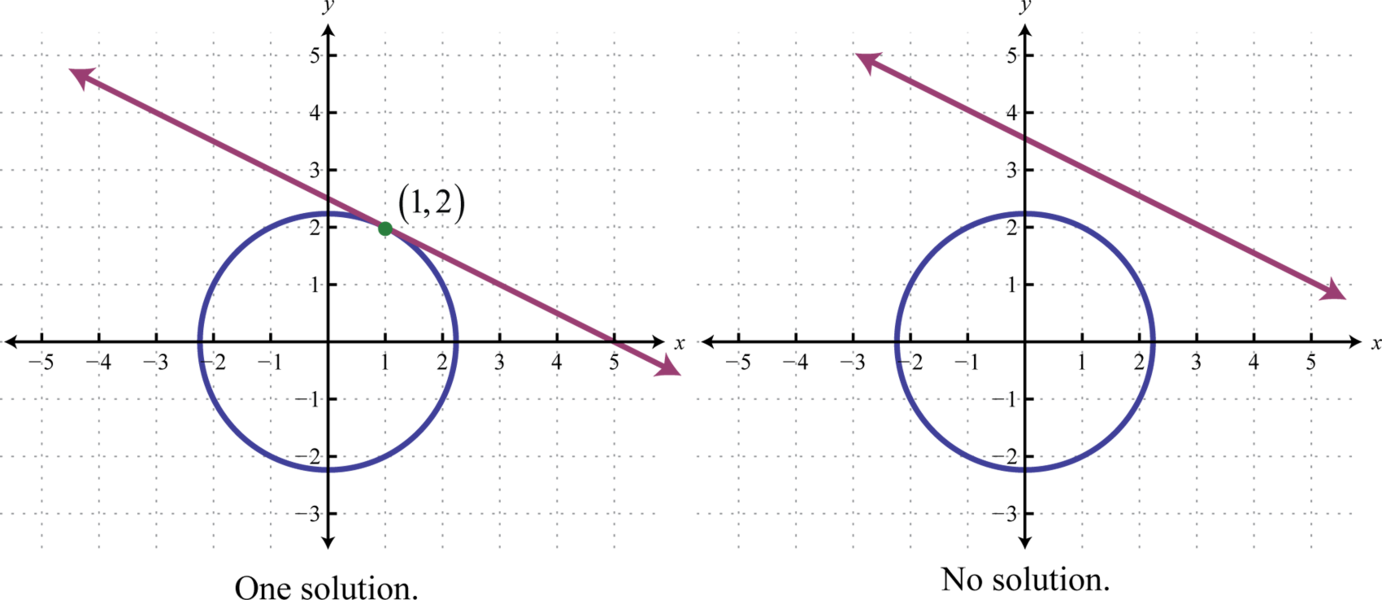
If we are given a system consisting of a circle and a line, then there are \(3\) possibilities for real solutions—two solutions as pictured above, one solution, or no solution.

Figure \(\PageIndex{2}\)

Example \(\PageIndex{2}\)

Solve: \(\left\{\begin{array}{c}{x+y=3} \\ {x^{2}+y^{2}=2}\end{array}\right.\).

Solution

Solve for \(y\) in the first equation.

\(\left\{\begin{array}{c}{x+y} \\ {x^{2}+y^{2}}\end{array}\right.\)

Next, substitute \(y=3−x\) into the second equation and then solve for \(x\).

\(\begin{array}{r}{x^{2}+(\color{Cerulean}{3-x}\color{black}{)}^{2}=2} \\ {x^{2}+9-6 x+x^{2}=2} \\ {2 x^{2}-6 x+9=2} \\ {2 x^{2}-6 x+7=0}\end{array}\)

The resulting equation does not factor. Furthermore, using \(a=2\),\( b=−6\), and \(c=7\) we can see that the discriminant is negative:

\(\begin{aligned} b^{2}-4 a c &=(-6)^{2}-4(2)(7) \\ &=36-56 \\ &=-20 \end{aligned}\)

We conclude that there are no real solutions to this equation and thus no solution to the system.

Answer:

\(Ø\)

Exercise \(\PageIndex{1}\)

Solve: \(\left\{\begin{aligned} x-y &=5 \\ x^{2}+(y+1)^{2} &=8 \end{aligned}\right.\)

Answer

\((2,−3)\)

www.youtube.com/v/ToIrjw-8SNA

If given a circle and a parabola, then there are \(5\) possibilities for solutions.

Figure \(\PageIndex{3}\)

Figure \(\PageIndex{4}\)

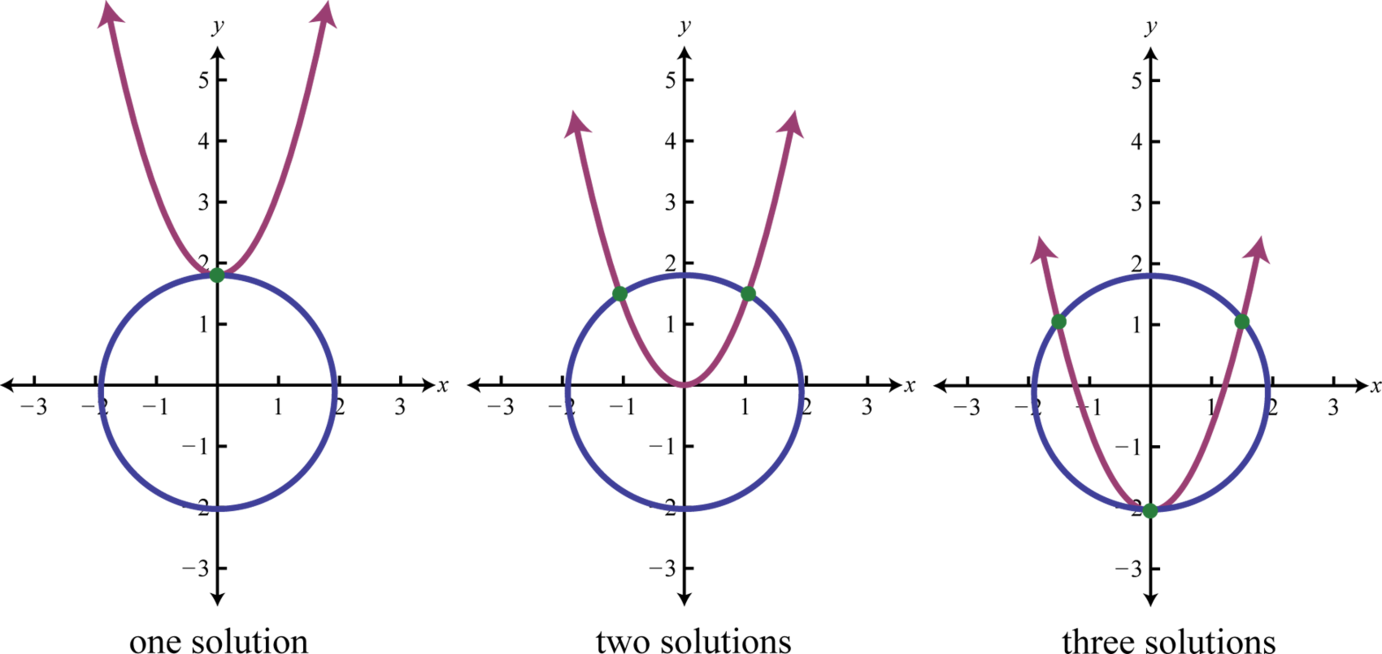
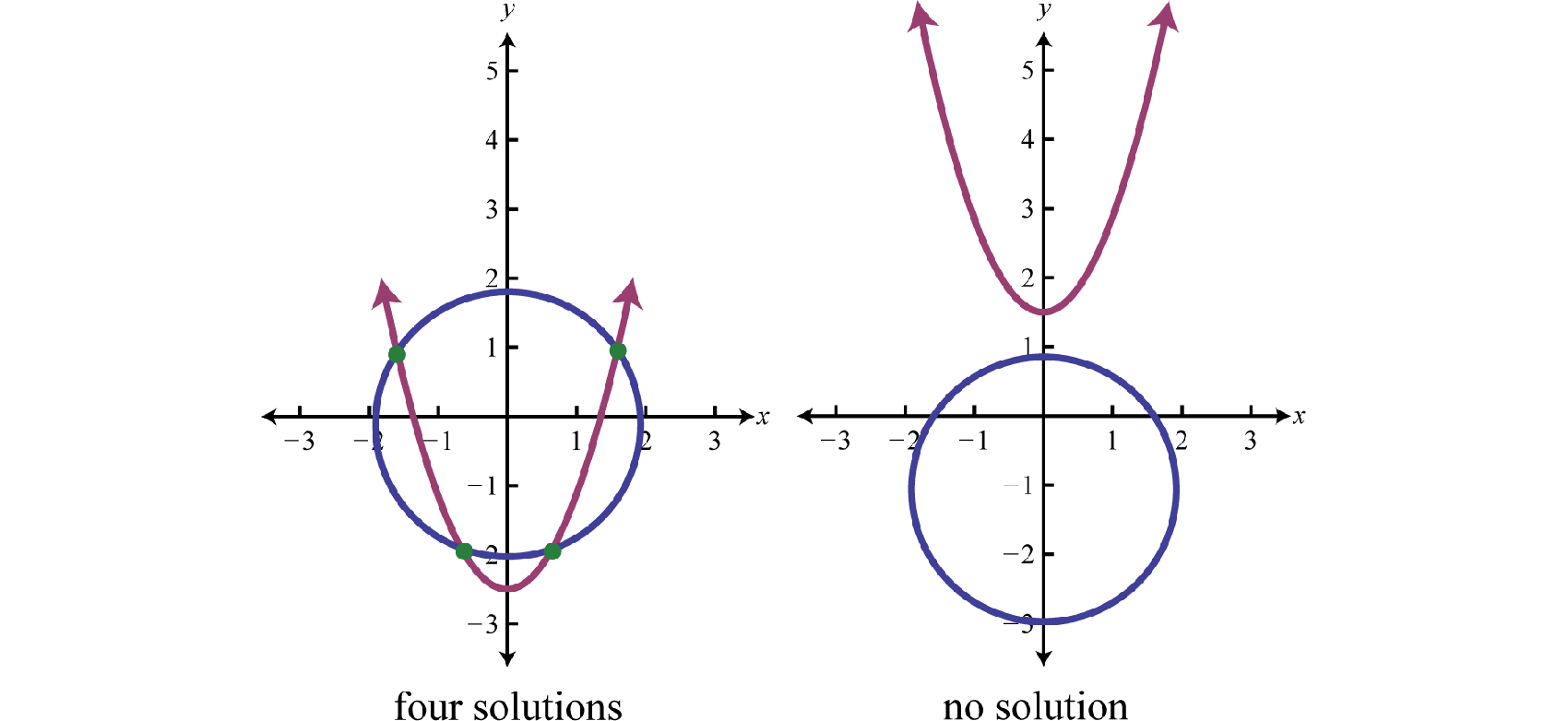
When using the substitution method, we can perform the substitution step using entire algebraic expressions. The goal is to produce a single equation in one variable that can be solved using the techniques learned up to this point in our study of algebra.

Example \(\PageIndex{3}\):

Solve: \(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2}\end{array}\right.\).

Solution

We can solve for \(x^{2}\) in the second equation.

\(\left\{\begin{array}{l}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2 \quad \Rightarrow \quad y+2=x^{2}}\end{array}\right.\)

Substitute \(x^{2}=y+2\) into the first equation and then solve for \(y\).

\(\begin{aligned} \color{Cerulean}{y+2}\color{black}{+}y^{2} &=2 \\ y^{2}+y &=0 \\ y(y+1) &=0 \\ y &=0 \quad \text { or } \quad y=-1 \end{aligned}\)

Back substitute into \(x^{2}=y+2\) to find the corresponding \(x\)-values.

Table \(\PageIndex{2}\)

Using \(y=-1\)	Using \(y=0\)
\(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{-1}\color{black}{+}2 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)	\(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{0}\color{black}{+}2 \\ x^{2} &=2 \\ x &=\pm \sqrt{2} \end{aligned}\)

This leads us to four solutions, \((±1,−1)\) and \((\pm \sqrt{2}, 0)\).

Answer:

\((\pm 1,-1),(\pm \sqrt{2}, 0)\)

Example \(\PageIndex{4}\)

Solve: \(\left\{\begin{aligned}(x-1)^{2}-2 y^{2} &=4 \\ x^{2}+y^{2} &=9 \end{aligned}\right.\)

Solution

We can solve for \(y^{2}\) in the second equation,

\(\left\{\begin{array}{r}{(x-1)^{2}-2 y^{2}=4} \\ {x^{2}+y^{2}=9}\end{array}\right. \Longrightarrow y^{2}=9-x^{2}\)

Substitute \(y^{2}=9−x^{2}\) into the first equation and then solve for \(x\).

\(\begin{aligned}(x-1)^{2}-2\color{black}{\left(\color{Cerulean}{9-x^{2}}\right) }&=4 \\ x^{2}-2 x+1-18+2 x^{2} &=0 \\ 3 x^{2}-2 x-21 &=0 \\(3 x+7)(x-3) &=0 \\ 3 x+7 &=0 \text { or } x-3=0 \\ x &=-\frac{7}{3} \quad x=3 \end{aligned}\)

Back substitute into \(y^{2}=9−x^{2}\) to find the corresponding \(y\)-values.

Table \(\PageIndex{3}\)

Using \(x=-\frac{7}{3}\)	Using \(x=3\)
\(\begin{array}{l}{y^{2}=9-\color{black}{\left(\color{Cerulean}{-\frac{7}{3}}\right)^{2}}} \\ {y^{2}=\frac{9}{1}-\frac{49}{9}} \\ {y^{2}=\frac{32}{9}} \\ {y=\pm \frac{\sqrt{32}}{3}=\pm \frac{4 \sqrt{2}}{3}}\end{array}\)	\(\begin{aligned} y^{2} &=9-(\color{Cerulean}{3}\color{black}{)}^{2} \\ y^{2} &=0 \\ y &=0 \end{aligned}\)

This leads to three solutions, \(\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\) and \((3,0)\).

Answer:

\((3,0),\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\)

Example \(\PageIndex{5}\)

Solve: \(\left\{\begin{aligned} x^{2}+y^{2} &=2 \\ x y &=1 \end{aligned}\right.\).

Solution

Solve for \(y\) in the second equation.

\(\left\{\begin{array}{r}{x^{2}+y^{2}=2} \\ {x y=1}\end{array}\right.\Longrightarrow y=\frac{1}{x}\)

Substitute \(y=\frac{1}{x}\) into the first equation and then solve for \(x\).

\(x^{2}+\left(\frac{1}{x}\right)^{2}=2\)
\(x^{2}+\frac{1}{x^{2}}=2\)

This leaves us with a rational equation. Make a note that \(x≠0\) and multiply both sides by \(x^{2}\).

\(\begin{aligned} \color{Cerulean}{x^{2}}\color{black}{\left(x^{2}+\frac{1}{x^{2}}\right)} &=2 \cdot \color{Cerulean}{x^{2}} \\ x^{4}+1 &=2 x^{2} \\ x^{4}-2 x^{2}+1 &=0 \\\left(x^{2}-1\right)\left(x^{2}-1\right) &=0 \end{aligned}\)

At this point we can see that both factors are the same. Apply the zero product property.

\(\begin{aligned} x^{2}-1 &=0 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)

Back substitute into \(y=\frac{1}{x}\) to find the corresponding \(y\)-values.

Using \(x=-1\)	Using \(x=1\)
\(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{-1}} \\ &=-1 \end{aligned}\)	\(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{1}} \\ &=1 \end{aligned}\)

This leads to two solutions.

Answer:

\((1,1),(-1,-1)\)

Exercise \(\PageIndex{2}\)

Solve: \(\left\{\begin{array}{r}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=40}\end{array}\right.\)

Answer

\(\left(-\frac{1}{2}, \frac{1}{6}\right)\left(\frac{1}{6},-\frac{1}{2}\right)\)

www.youtube.com/v/n8JJ_ybegkM

Key Takeaways

• Use the substitution method to solve nonlinear systems.
• Streamline the solving process by using entire algebraic expressions in the substitution step to obtain a single equation with one variable.
• Understanding the geometric interpretation of the system can help in finding real solutions.

Footnotes

³²A system of equations where at least one equation is not linear.