Skip to main content
Mathematics LibreTexts

8.5: Solving Nonlinear Systems

  1. Last updated
  2. Save as PDF
  • Page ID
    6286
    • Anonymous
    • LibreTexts

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Learning Objectives

    • Identify nonlinear systems.
    • Solve nonlinear systems using the substitution method.

    Nonlinear Systems

    A system of equations where at least one equation is not linear is called a nonlinear system32. In this section we will use the substitution method to solve nonlinear systems. Recall that solutions to a system with two variables are ordered pairs \((x,y)\) that satisfy both equations.

    Example \(\PageIndex{1}\):

    Solve: \(\left\{\begin{array}{l}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\right.\).

    Solution

    In this case we begin by solving for x in the first equation.

    \(\left\{\begin{array}{c}{x+2 y=0} \\ {x^{2}+y^{2}=5}\end{array}\Longrightarrow x=-2y \right.\)

    Substitute \(x=−2y\) into the second equation and then solve for \(y\).

    \(\begin{aligned}(\color{Cerulean}{-2y }\color{black}{)}^{2}+y^{2} &=5 \\ 4 y^{2}+y^{2} &=5 \\ 5 y^{2} &=5 \\ y^{2} &=1 \\ y &=\pm 1 \end{aligned}\)

    Here there are two answers for \(y\); use \(x=−2y\) to find the corresponding \(x\)-values.

    Using \(y=-1\) Using \(y=1\)
    \(\begin{aligned} x &=-2 y \\ &=-2(-1) \\ &=2 \end{aligned}\) \(\begin{aligned} x &=-2 y \\ &=-2(1) \\ &=-2 \end{aligned}\)
    Table \(\PageIndex{1}\)

    This gives us two ordered pair solutions, \((2,−1)\) and \((−2,1)\).

    Answer:

    \((2,−1), (−2,1)\)

    In the previous example, the given system consisted of a line and a circle. Graphing these equations on the same set of axes, we can see that the two ordered pair solutions correspond to the two points of intersection.

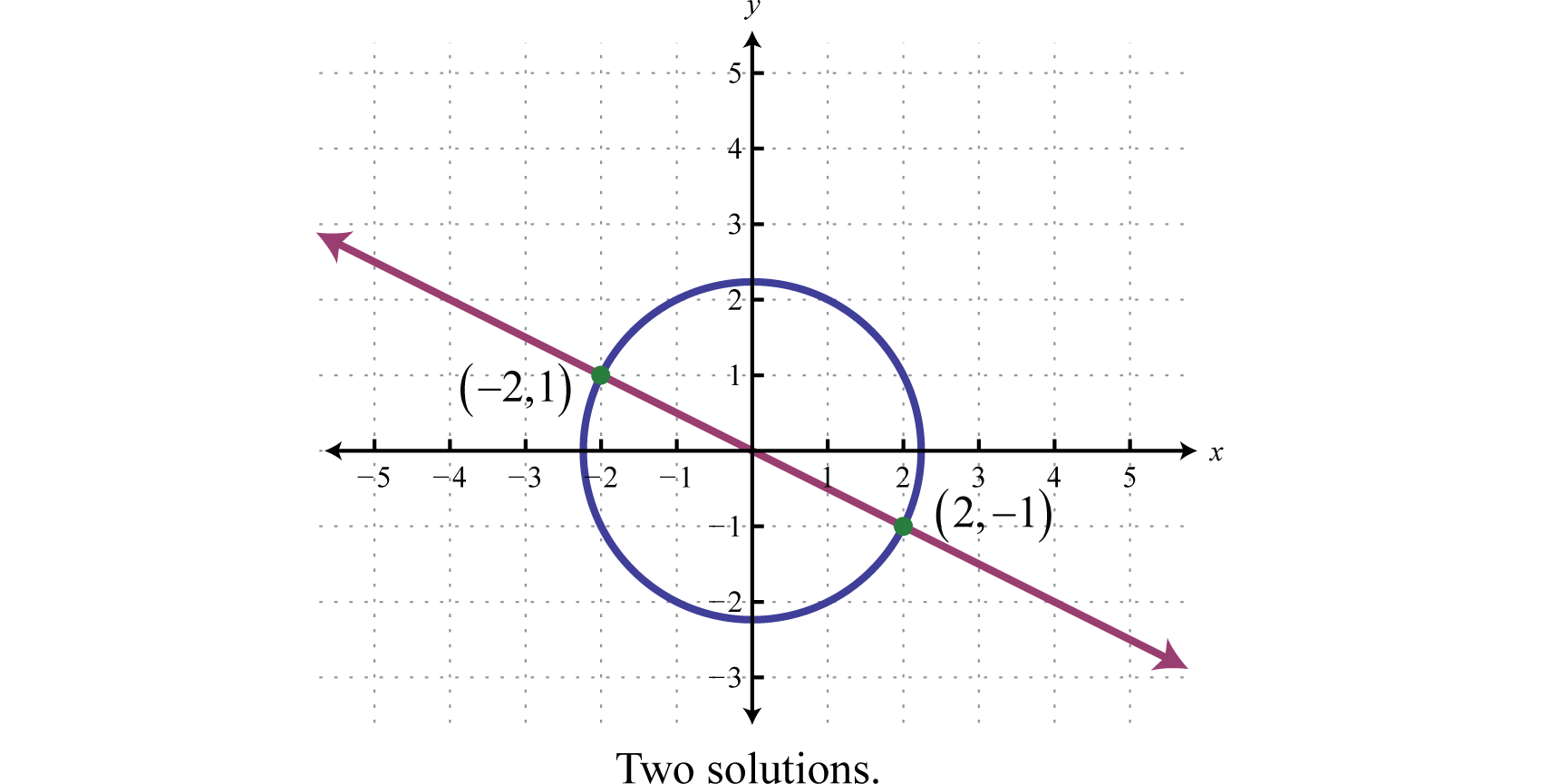
    63cc6b5695c23d927ccfa192d8058ce9.png
    Figure \(\PageIndex{1}\)

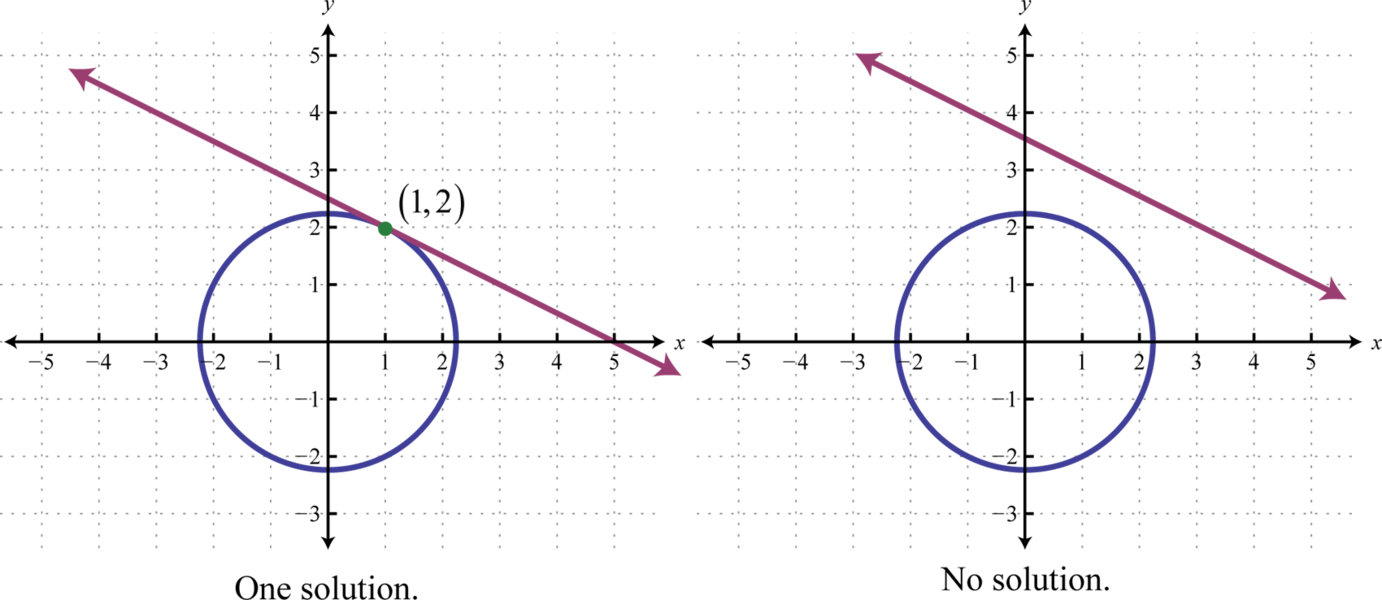
    If we are given a system consisting of a circle and a line, then there are \(3\) possibilities for real solutions—two solutions as pictured above, one solution, or no solution.

    d86c2e39a716bdb8f6872d5af93ec4ed.png
    Figure \(\PageIndex{2}\)

    Example \(\PageIndex{2}\)

    Solve: \(\left\{\begin{array}{c}{x+y=3} \\ {x^{2}+y^{2}=2}\end{array}\right.\).

    Solution

    Solve for \(y\) in the first equation.

    \(\left\{\begin{array}{c}{x+y} \\ {x^{2}+y^{2}}\end{array}\right.\)

    Next, substitute \(y=3−x\) into the second equation and then solve for \(x\).

    \(\begin{array}{r}{x^{2}+(\color{Cerulean}{3-x}\color{black}{)}^{2}=2} \\ {x^{2}+9-6 x+x^{2}=2} \\ {2 x^{2}-6 x+9=2} \\ {2 x^{2}-6 x+7=0}\end{array}\)

    The resulting equation does not factor. Furthermore, using \(a=2\),\( b=−6\), and \(c=7\) we can see that the discriminant is negative:

    \(\begin{aligned} b^{2}-4 a c &=(-6)^{2}-4(2)(7) \\ &=36-56 \\ &=-20 \end{aligned}\)

    We conclude that there are no real solutions to this equation and thus no solution to the system.

    Answer:

    \(Ø\)

    Exercise \(\PageIndex{1}\)

    Solve: \(\left\{\begin{aligned} x-y &=5 \\ x^{2}+(y+1)^{2} &=8 \end{aligned}\right.\)

    Answer

    \((2,−3)\)

    www.youtube.com/v/ToIrjw-8SNA

    If given a circle and a parabola, then there are \(5\) possibilities for solutions.

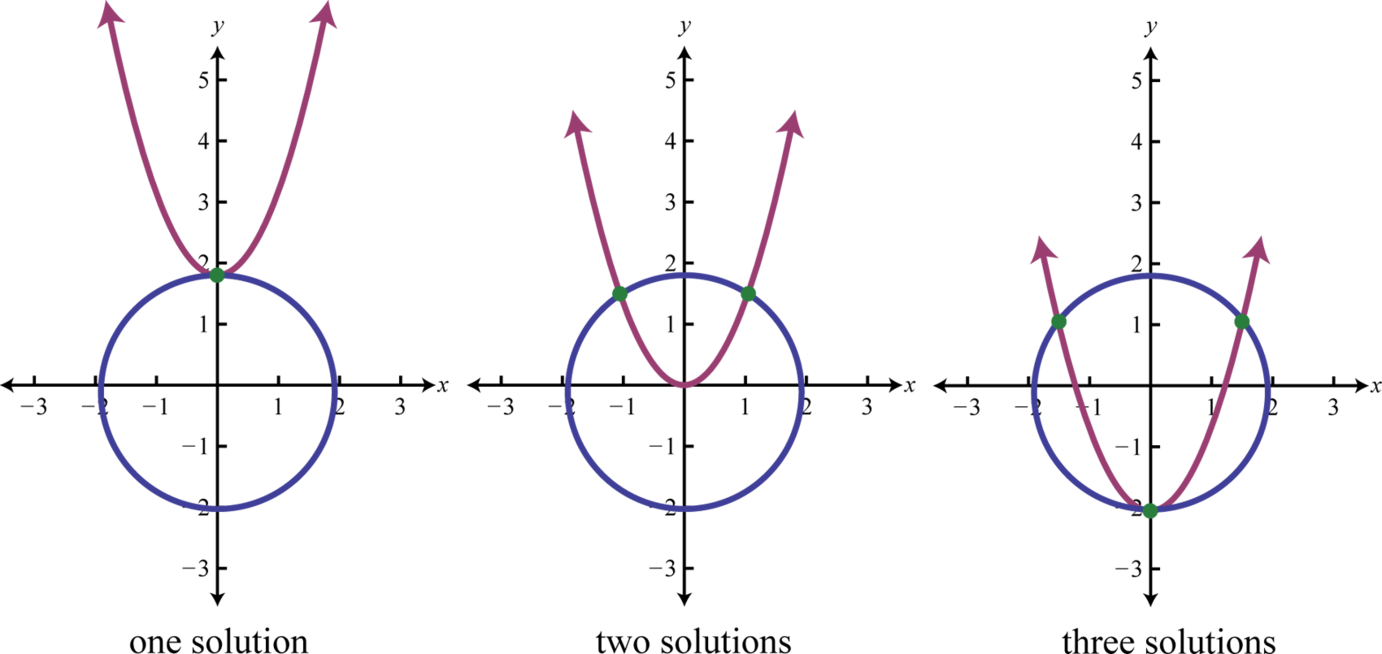
    6f0b7f93046f8792455c1e949553193f.png
    Figure \(\PageIndex{3}\)
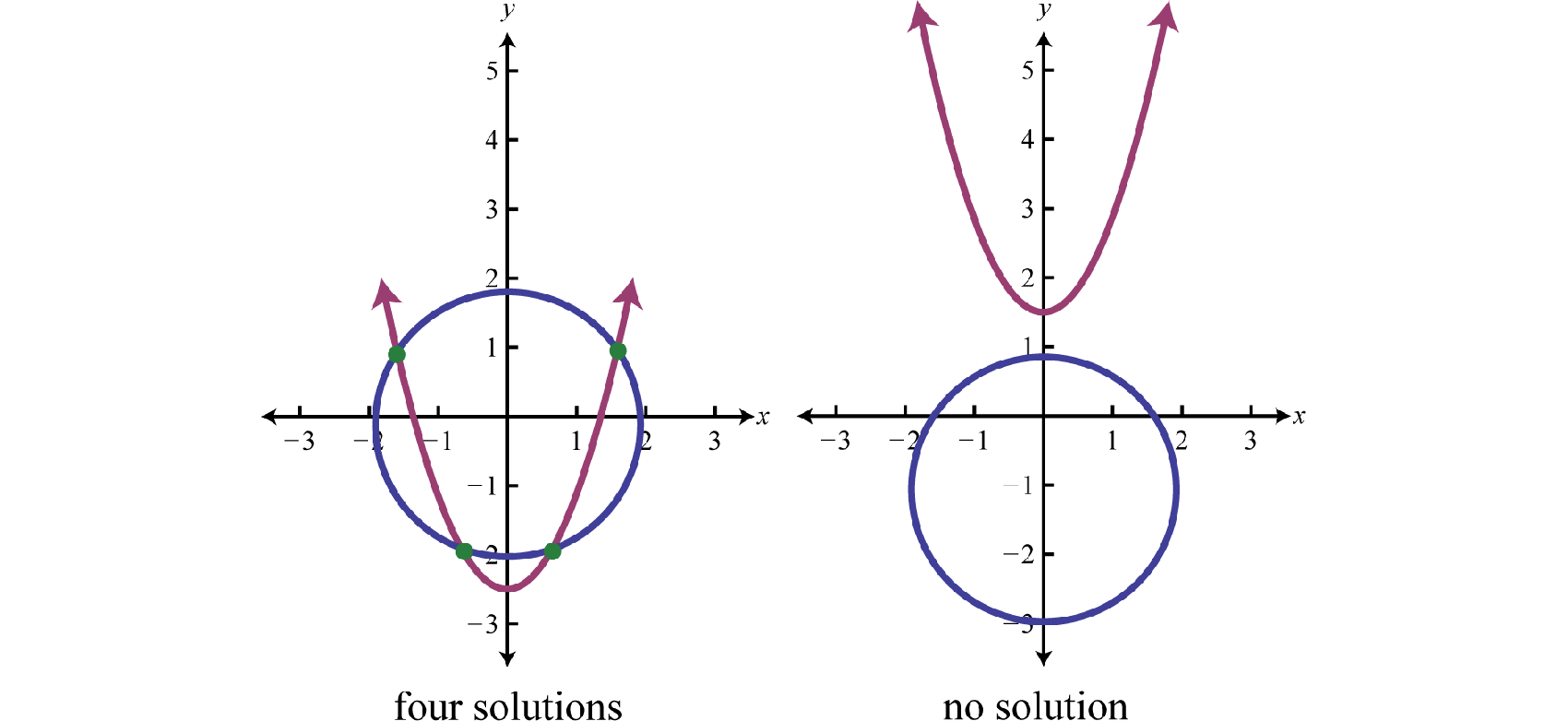
    55805918d45b660465c7ce19545b3b1f.png
    Figure \(\PageIndex{4}\)

    When using the substitution method, we can perform the substitution step using entire algebraic expressions. The goal is to produce a single equation in one variable that can be solved using the techniques learned up to this point in our study of algebra.

    Example \(\PageIndex{3}\):

    Solve: \(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2}\end{array}\right.\).

    Solution

    We can solve for \(x^{2}\) in the second equation.

    \(\left\{\begin{array}{l}{x^{2}+y^{2}=2} \\ {y-x^{2}=-2 \quad \Rightarrow \quad y+2=x^{2}}\end{array}\right.\)

    Substitute \(x^{2}=y+2\) into the first equation and then solve for \(y\).

    \(\begin{aligned} \color{Cerulean}{y+2}\color{black}{+}y^{2} &=2 \\ y^{2}+y &=0 \\ y(y+1) &=0 \\ y &=0 \quad \text { or } \quad y=-1 \end{aligned}\)

    Back substitute into \(x^{2}=y+2\) to find the corresponding \(x\)-values.

    Table \(\PageIndex{2}\)
    Using \(y=-1\) Using \(y=0\)
    \(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{-1}\color{black}{+}2 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\) \(\begin{aligned} x^{2} &=y+2 \\ x^{2} &=\color{Cerulean}{0}\color{black}{+}2 \\ x^{2} &=2 \\ x &=\pm \sqrt{2} \end{aligned}\)

    This leads us to four solutions, \((±1,−1)\) and \((\pm \sqrt{2}, 0)\).

    Answer:

    \((\pm 1,-1),(\pm \sqrt{2}, 0)\)

    Example \(\PageIndex{4}\)

    Solve: \(\left\{\begin{aligned}(x-1)^{2}-2 y^{2} &=4 \\ x^{2}+y^{2} &=9 \end{aligned}\right.\)

    Solution

    We can solve for \(y^{2}\) in the second equation,

    \(\left\{\begin{array}{r}{(x-1)^{2}-2 y^{2}=4} \\ {x^{2}+y^{2}=9}\end{array}\right. \Longrightarrow y^{2}=9-x^{2}\)

    Substitute \(y^{2}=9−x^{2}\) into the first equation and then solve for \(x\).

    \(\begin{aligned}(x-1)^{2}-2\color{black}{\left(\color{Cerulean}{9-x^{2}}\right) }&=4 \\ x^{2}-2 x+1-18+2 x^{2} &=0 \\ 3 x^{2}-2 x-21 &=0 \\(3 x+7)(x-3) &=0 \\ 3 x+7 &=0 \text { or } x-3=0 \\ x &=-\frac{7}{3} \quad x=3 \end{aligned}\)

    Back substitute into \(y^{2}=9−x^{2}\) to find the corresponding \(y\)-values.

    Table \(\PageIndex{3}\)
    Using \(x=-\frac{7}{3}\) Using \(x=3\)
    \(\begin{array}{l}{y^{2}=9-\color{black}{\left(\color{Cerulean}{-\frac{7}{3}}\right)^{2}}} \\ {y^{2}=\frac{9}{1}-\frac{49}{9}} \\ {y^{2}=\frac{32}{9}} \\ {y=\pm \frac{\sqrt{32}}{3}=\pm \frac{4 \sqrt{2}}{3}}\end{array}\) \(\begin{aligned} y^{2} &=9-(\color{Cerulean}{3}\color{black}{)}^{2} \\ y^{2} &=0 \\ y &=0 \end{aligned}\)

    This leads to three solutions, \(\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\) and \((3,0)\).

    Answer:

    \((3,0),\left(-\frac{7}{3}, \pm \frac{4 \sqrt{2}}{3}\right)\)

    Example \(\PageIndex{5}\)

    Solve: \(\left\{\begin{aligned} x^{2}+y^{2} &=2 \\ x y &=1 \end{aligned}\right.\).

    Solution

    Solve for \(y\) in the second equation.

    \(\left\{\begin{array}{r}{x^{2}+y^{2}=2} \\ {x y=1}\end{array}\right.\Longrightarrow y=\frac{1}{x}\)

    Substitute \(y=\frac{1}{x}\) into the first equation and then solve for \(x\).

    \(x^{2}+\left(\frac{1}{x}\right)^{2}=2\)
    \(x^{2}+\frac{1}{x^{2}}=2\)

    This leaves us with a rational equation. Make a note that \(x≠0\) and multiply both sides by \(x^{2}\).

    \(\begin{aligned} \color{Cerulean}{x^{2}}\color{black}{\left(x^{2}+\frac{1}{x^{2}}\right)} &=2 \cdot \color{Cerulean}{x^{2}} \\ x^{4}+1 &=2 x^{2} \\ x^{4}-2 x^{2}+1 &=0 \\\left(x^{2}-1\right)\left(x^{2}-1\right) &=0 \end{aligned}\)

    At this point we can see that both factors are the same. Apply the zero product property.

    \(\begin{aligned} x^{2}-1 &=0 \\ x^{2} &=1 \\ x &=\pm 1 \end{aligned}\)

    Back substitute into \(y=\frac{1}{x}\) to find the corresponding \(y\)-values.

    Using \(x=-1\) Using \(x=1\)
    \(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{-1}} \\ &=-1 \end{aligned}\) \(\begin{aligned} y &=\frac{1}{x} \\ &=\frac{1}{\color{Cerulean}{1}} \\ &=1 \end{aligned}\)

    This leads to two solutions.

    Answer:

    \((1,1),(-1,-1)\)

    Exercise \(\PageIndex{2}\)

    Solve: \(\left\{\begin{array}{r}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=40}\end{array}\right.\)

    Answer

    \(\left(-\frac{1}{2}, \frac{1}{6}\right)\left(\frac{1}{6},-\frac{1}{2}\right)\)

    www.youtube.com/v/n8JJ_ybegkM

    Key Takeaways

    • Use the substitution method to solve nonlinear systems.
    • Streamline the solving process by using entire algebraic expressions in the substitution step to obtain a single equation with one variable.
    • Understanding the geometric interpretation of the system can help in finding real solutions.

    Exercise \(\PageIndex{3}\)

    Solve.

    1. \(\left\{\begin{array}{c}{x^{2}+y^{2}=10} \\ {x+y=4}\end{array}\right.\)
    2. \(\left\{\begin{array}{c}{x^{2}+y^{2}=5} \\ {x-y=-3}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{x^{2}+y^{2}=30} \\ {x-3 y=0}\end{array}\right.\)
    4. \(\left\{\begin{array}{c}{x^{2}+y^{2}=10} \\ {2 x-y=0}\end{array}\right.\)
    5. \(\left\{\begin{array}{c}{x^{2}+y^{2}=18} \\ {2 x-2 y=-12}\end{array}\right.\)
    6. \(\left\{\begin{aligned}(x-4)^{2}+y^{2} &=25 \\ 4 x-3 y &=16 \end{aligned}\right.\)
    7. \(\left\{\begin{array}{c}{3 x^{2}+2 y^{2}=21} \\ {3 x-y=0}\end{array}\right.\)
    8. \(\left\{\begin{aligned} x^{2}+5 y^{2} &=36 \\ x-2 y &=0 \end{aligned}\right.\)
    9. \(\left\{\begin{array}{c}{4 x^{2}+9 y^{2}=36} \\ {2 x+3 y=6}\end{array}\right.\)
    10. \(\left\{\begin{array}{c}{4 x^{2}+y^{2}=4} \\ {2 x+y=-2}\end{array}\right.\)
    11. \(\left\{\begin{array}{c}{2 x^{2}+y^{2}=1} \\ {x+y=1}\end{array}\right.\)
    12. \(\left\{\begin{array}{c}{4 x^{2}+3 y^{2}=12} \\ {2 x-y=2}\end{array}\right.\)
    13. \(\left\{\begin{aligned} x^{2}-2 y^{2} &=35 \\ x-3 y &=0 \end{aligned}\right.\)
    14. \(\left\{\begin{array}{c}{5 x^{2}-7 y^{2}=39} \\ {2 x+4 y=0}\end{array}\right.\)
    15. \(\left\{\begin{array}{c}{9 x^{2}-4 y^{2}=36} \\ {3 x+2 y=0}\end{array}\right.\)
    16. \(\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {x-2 y=-12}\end{array}\right.\)
    17. \(\left\{\begin{array}{l}{2 x^{2}+3 y=9} \\ {8 x-4 y=12}\end{array}\right.\)
    18. \(\left\{\begin{array}{l}{2 x-4 y^{2}=3} \\ {3 x-12 y=6}\end{array}\right.\)
    19. \(\left\{\begin{aligned} 4 x^{2}+3 y^{2} &=12 \\ x-\frac{3}{2} &=0 \end{aligned}\right.\)
    20. \(\left\{\begin{aligned} 5 x^{2}+4 y^{2} &=40 \\ y-3 &=0 \end{aligned}\right.\)
    21. The sum of the squares of two positive integers is \(10\). If the first integer is added to twice the second integer, the sum is \(7\). Find the integers.
    22. The diagonal of a rectangle measures \(\sqrt{5}\) units and has a perimeter equal to \(6\) units. Find the dimensions of the rectangle.
    23. For what values of \(b\) will the following system have real solutions? \(\left\{\begin{array}{c}{x^{2}+y^{2}=1} \\ {y=x+b}\end{array}\right.\)
    24. For what values of \(m\) will be the following system have real solutions? \(\left\{\begin{array}{c}{x^{2}-y^{2}=1} \\ {y=m x}\end{array}\right.\)
    Answer

    1. \((1,3),(3,1)\)

    3. \((-3 \sqrt{3},-\sqrt{3}),(3 \sqrt{3}, \sqrt{3})\)

    5. \((-3,3)\)

    7. \((-1,-3),(1,3)\)

    9. \((0,2),(3,0)\)

    11. \((0,1),\left(\frac{2}{3}, \frac{1}{3}\right)\)

    13. \((-3 \sqrt{5},-\sqrt{5}),(3 \sqrt{5}, \sqrt{5})\)

    15. \(\emptyset\)

    17. \(\left(\frac{-3+3 \sqrt{5}}{2},-6+3 \sqrt{5}\right) ,\left(\frac{-3-3 \sqrt{5}}{2},-6-3 \sqrt{5}\right)\)

    19. \(\left(\frac{3}{2},-1\right),\left(\frac{3}{2}, 1\right)\)

    21. \(1,3\)

    23. \(b \in[-\sqrt{2}, \sqrt{2}]\)

    Exercise \(\PageIndex{4}\)

    Solve.

    1. \(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {y-x^{2}=2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {y-x^{2}=-2}\end{array}\right.\)
    3. \(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {y-x^{2}=3}\end{array}\right.\)
    4. \(\left\{\begin{array}{c}{x^{2}+y^{2}=4} \\ {4 y-x^{2}=-4}\end{array}\right.\)
    5. \(\left\{\begin{array}{c}{x^{2}+3 y^{2}=9} \\ {y^{2}-x=3}\end{array}\right.\)
    6. \(\left\{\begin{array}{c}{x^{2}+3 y^{2}=9} \\ {x+y^{2}=-4}\end{array}\right.\)
    7. \(\left\{\begin{aligned} 4 x^{2}-3 y^{2} &=12 \\ x^{2}+y^{2} &=1 \end{aligned}\right.\)
    8. \(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
    9. \(\left\{\begin{aligned} x^{2}+y^{2} &=1 \\ 4 y^{2}-x^{2}-4 y &=0 \end{aligned}\right.\)
    10. \(\left\{\begin{aligned} x^{2}+y^{2} &=4 \\ 2 x^{2}-y^{2}+4 x &=0 \end{aligned}\right.\)
    11. \(\left\{\begin{aligned} 2(x-2)^{2}+y^{2} &=6 \\(x-3)^{2}+y^{2} &=4 \end{aligned}\right.\)
    12. \(\left\{\begin{array}{c}{x^{2}+y^{2}-6 y=0} \\ {4 x^{2}+5 y^{2}+20 y=0}\end{array}\right.\)
    13. \(\left\{\begin{array}{l}{x^{2}+4 y^{2}=25} \\ {4 x^{2}+y^{2}=40}\end{array}\right.\)
    14. \(\left\{\begin{array}{c}{x^{2}-2 y^{2}=-10} \\ {4 x^{2}+y^{2}=10}\end{array}\right.\)
    15. \(\left\{\begin{array}{c}{2 x^{2}+y^{2}=14} \\ {x^{2}-(y-1)^{2}=6}\end{array}\right.\)
    16. \(\left\{\begin{array}{c}{3 x^{2}-(y-2)^{2}=12} \\ {x^{2}+(y-2)^{2}=1}\end{array}\right.\)
    17. The difference of the squares of two positive integers is \(12\). The sum of the larger integer and the square of the smaller is equal to \(8\). Find the integers.
    18. The difference between the length and width of a rectangle is \(4\) units and the diagonal measures \(8\) units. Find the dimensions of the rectangle. Round off to the nearest tenth.
    19. The diagonal of a rectangle measures \(p\) units and has a perimeter equal to \(2q\) units. Find the dimensions of the rectangle in terms of \(p\) and \(q\).
    20. The area of a rectangle is \(p\) square units and its perimeter is \(2q\) units. Find the dimensions of the rectangle in terms of \(p\) and \(q\).
    Answer

    1. \((0,2)\)

    3. \(\emptyset\)

    5. \((-3,0),(0,-\sqrt{3}),(0, \sqrt{3})\)

    7. \(\emptyset\)

    9. \((0,1),\left(-\frac{2 \sqrt{5}}{5},-\frac{1}{5}\right),\left(\frac{2 \sqrt{5}}{5},-\frac{1}{5}\right)\)

    11. \((3,-2),(3,2)\)

    13. \((-3,-2),(-3,2),(3,-2),(3,2)\)

    15. \((-\sqrt{7}, 0),(\sqrt{7}, 0),\left(-\frac{\sqrt{55}}{3}, \frac{4}{3}\right),\left(\frac{\sqrt{55}}{3}, \frac{4}{3}\right)\)

    17. \(2,4\)

    19. \(\frac{q+\sqrt{2 p^{2}-q^{2}}}{2}\) units by \(\frac{q-\sqrt{2 p^{2}-q^{2}}}{2}\) units

    Exercise \(\PageIndex{5}\)

    Solve.

    1. \(\left\{\begin{aligned} x^{2}+y^{2} &=26 \\ x y &=5 \end{aligned}\right.\)
    2. \(\left\{\begin{aligned} x^{2}+y^{2} &=10 \\ x y &=3 \end{aligned}\right.\)
    3. \(\left\{\begin{aligned} 2 x^{2}-3 y^{2} &=5 \\ x y &=1 \end{aligned}\right.\)
    4. \(\left\{\begin{array}{c}{3 x^{2}-4 y^{2}=-11} \\ {x y=1}\end{array}\right.\)
    5. \(\left\{\begin{array}{c}{x^{2}+y^{2}=2} \\ {x y-2=0}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {2 x y-1=0}\end{array}\right.\)
    7. \(\left\{\begin{aligned} 4 x-y^{2} &=0 \\ x y &=2 \end{aligned}\right.\)
    8. \(\left\{\begin{array}{c}{3 y-x^{2}=0} \\ {x y-9=0}\end{array}\right.\)
    9. \(\left\{\begin{aligned} 2 y-x^{2} &=0 \\ x y-1 &=0 \end{aligned}\right.\)
    10. \(\left\{\begin{aligned} x-y^{2} &=0 \\ x y &=3 \end{aligned}\right.\)
    11. The diagonal of a rectangle measures \(2\sqrt{10}\) units. If the area of the rectangle is \(12\) square units, find its dimensions.
    12. The area of a rectangle is \(48\) square meters and the perimeter measures \(32\) meters. Find the dimensions of the rectangle.
    13. The product of two positive integers is \(72\) and their sum is \(18\). Find the integers.
    14. The sum of the squares of two positive integers is \(52\) and their product is \(24\). Find the integers.
    Answer

    1. \((-5,-1),(5,1),(-1,-5),(1,5)\)

    3. \(\left(-\sqrt{3},-\frac{\sqrt{3}}{3}\right),\left(\sqrt{3}, \frac{\sqrt{3}}{3}\right)\)

    5. \(\emptyset\)

    7. \((1,2)\)

    9. \(\left(\sqrt[3]{2}, \frac{\sqrt[3]{4}}{2}\right)\)

    11. \(2\) units by \(6\) units

    13. \(6,12\)

    Exercise \(\PageIndex{6}\)

    Solve.

    1. \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=4} \\ {\frac{1}{x}-\frac{1}{y}=2}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{\frac{2}{x}-\frac{1}{y}=5} \\ {\frac{1}{x}+\frac{1}{y}=2}\end{array}\right.\)
    3. \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{2}{y}=1} \\ {\frac{3}{x}-\frac{1}{y}=2}\end{array}\right.\)
    4. \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=6} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=20}\end{array}\right.\)
    5. \(\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=2} \\ {\frac{1}{x^{2}}+\frac{1}{y^{2}}=34}\end{array}\right.\)
    6. \(\left\{\begin{array}{l}{x y-16=0} \\ {2 x^{2}-y=0}\end{array}\right.\)
    7. \(\left\{\begin{array}{l}{x+y^{2}=4} \\ {y=\sqrt{x}}\end{array}\right.\)
    8. \(\left\{\begin{array}{c}{y^{2}-(x-1)^{2}=1} \\ {y=\sqrt{x}}\end{array}\right.\)
    9. \(\left\{\begin{array}{l}{y=2^{x}} \\ {y=2^{2 x}-56}\end{array}\right.\)
    10. \(\left\{\begin{array}{l}{y=3^{2 x}-72} \\ {y-3^{x}=0}\end{array}\right.\)
    11. \(\left\{\begin{array}{l}{y=e^{4 x}} \\ {y=e^{2 x}+6}\end{array}\right.\)
    12. \(\left\{\begin{array}{l}{y-e^{2 x}=0} \\ {y-e^{x}=0}\end{array}\right.\)
    Answer

    1. \(\left(\frac{1}{3}, 1\right)\)

    3. \(\left(\frac{7}{5}, 7\right)\)

    5. \(\left(-\frac{1}{3}, \frac{1}{5}\right),\left(\frac{1}{5},-\frac{1}{3}\right)\)

    7. \((2, \sqrt{2})\)

    9. \((3,8)\)

    11. \(\left(\frac{\ln 3}{2}, 9\right)\)

    Exercise \(\PageIndex{7}\)

    1. How many real solutions can be obtained from a system that consists of a circle and a hyperbola? Explain.
    2. Make up your own nonlinear system, solve it, and provide the answer. Also, provide a graph and discuss the geometric interpretation of the solutions.
    Answer

    1. Answer may vary

    Footnotes

    32A system of equations where at least one equation is not linear.

    This page titled 8.5: Solving Nonlinear Systems is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by Anonymous via source content that was edited to the style and standards of the LibreTexts platform.