10.1.3.1: Multiplying Whole Numbers and Applications
- Page ID
- 113211
- Use three different ways to represent multiplication.
- Multiply whole numbers.
- Multiply whole numbers by a power of 10.
- Use rounding to estimate products.
- Find the area of a rectangle.
- Solve application problems using multiplication.
Introduction
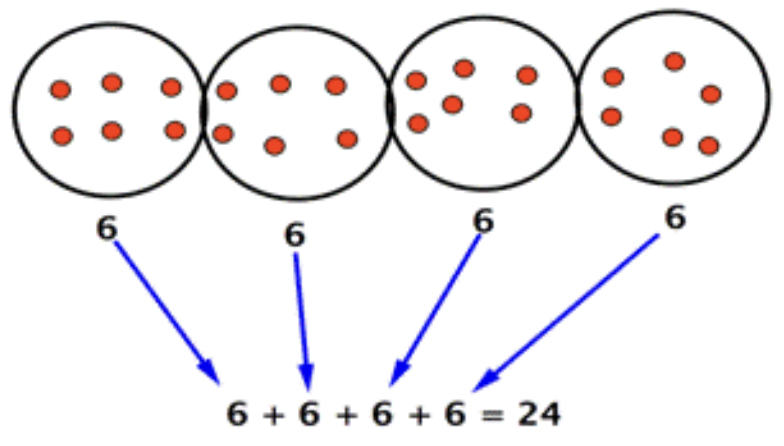
Instead of adding the same number over and over again, an easier way to reach an answer is to use multiplication. Suppose you want to find the value in pennies of 9 nickels. You can use addition to figure this out. Since a nickel is worth 5 pennies, or 5 cents, you can find the value of 9 nickels by adding 5+5+5+5+5+5+5+5+5. This repeated addition shows that 9 nickels have a value of 45 cents.
All of this addition can become very tiring. So, the math operation called multiplication can help perform repeated addition of whole numbers much more quickly. To find the value of these nickels, you could write a multiplication equation: \(\ 5 \cdot 9=45\).
\(\ 5 \cdot 9=45\) is read “5 times 9 equals 45" or "5 multiplied by 9 is equal to 45." The numbers that are being multiplied are called factors. The factors in this example are 5 and 9. The result of the multiplication (or the answer) is called the product. The product for \(\ 5 \cdot 9\) is 45.
In addition to showing multiplication as \(\ 5 \cdot 9=45\), you can show multiplication by using the x sign, \(\ 5 \times 9=45\), and also with parentheses, (5) (9) = 45 or 5(9)=45.
Three Ways to Write Multiplication
Using a multiplication or times sign: \(\ 2 \times 3=6\)
Using a dot: \(\ 2 \cdot 3=6\) (this dot is NOT a decimal point)
Using parentheses: (2)(3)=6 or 2(3)=6
When you are adding the same number over and over again, you can use multiplication. You take the number that you are adding and rewrite it as a multiplication problem, multiplying it by the number of times you are adding it. For example, if you were serving 2 cookies each to 13 children, you could add 2 thirteen times or you could use multiplication to find the answer.
\(\ 2+2+2+2+2+2+2+2+2+2+2+2+2=2 \cdot 13=26\)
You could also write this using parentheses: \(\ 2(13)=26\)
What Is Multiplication?
In order to understand what multiplication is, consider three different ways to think about multiplication of whole numbers.
Approach 1: Set Model
Multiplication is a way of writing repeated addition. When you read the problem \(\ 3 \cdot 5\) you could think of this as 3 groups of 5 things: 3 plates with 5 cookies on each plate; 3 baskets, each with 5 oranges in it; or 3 piles with 5 coins in each pile. We could show this as a picture:
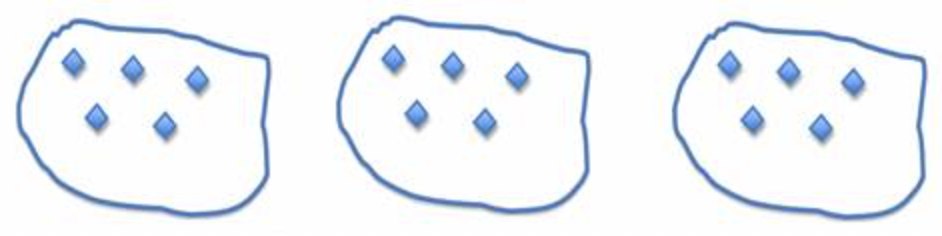
\(\ 3 \cdot 5=3\) groups of \(\ 5=15\)
Approach 2: Number Line Model
Multiplication can also be shown on a number line. The problem, \(\ 3 \cdot 5\) is modeled on the number line below. You can see that the arrows cover a distance of 5 units at a time. After 3 “jumps” on the number line, the arrow ends at 15.
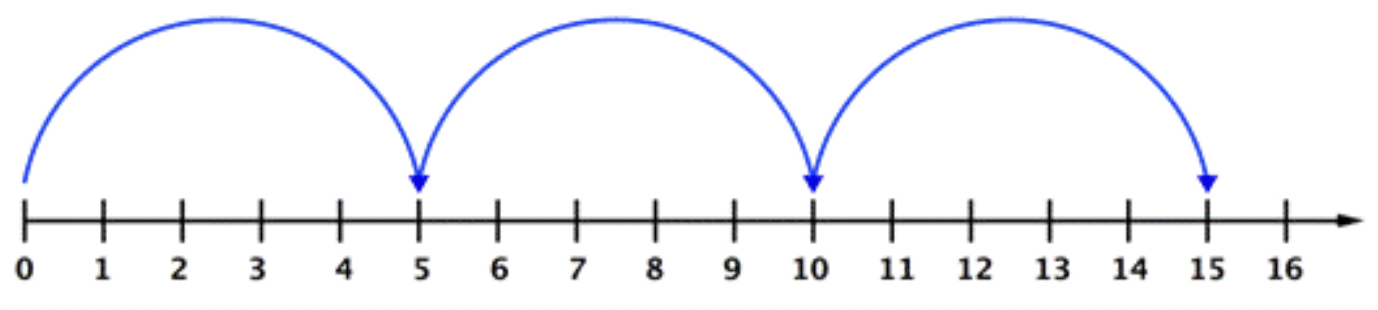
Approach 3: Area Model
Another way of thinking about multiplication is to think about an array or area model to represent multiplication. You could think of \(\ 3 \cdot 5\) as 3 rows of 5 things. This might be a box of chocolates that has 3 rows of 5 chocolates, or a meeting room that is set up with 3 rows of 5 chairs. The pictures below show two rectangular arrangements of \(\ 3 \cdot 5\).
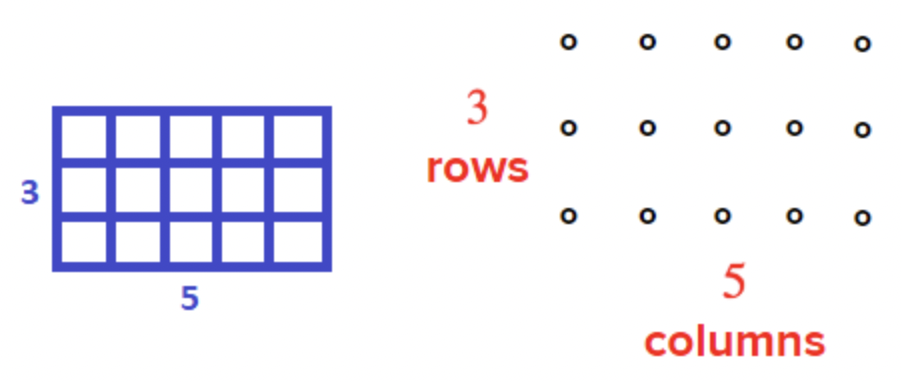
Do you see how both pictures represent the product 15? The picture on the left shows an area of 3 by 5. If you count the small squares that make up the rectangle, they total 15. Similarly, in the picture on the right, you see that 3 rows of 5 circles is equal to 15 circles.
What is the product of \(\ 4 \cdot 6\)? Use the set model, number line model and area model to represent the multiplication problem.
Solution
Set Model:
Number Line model:
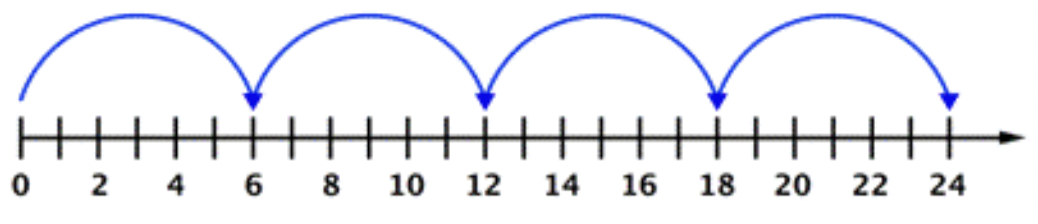
Area Model:
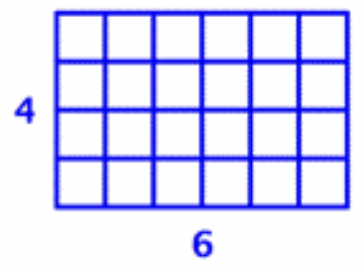
\(\ 4 \cdot 6=24\)
If you switch the order in which you multiply two numbers, the product will not change. This is true for any two numbers you multiply. Think about the problem shown above.
You could make 6 jumps of 4 or 4 jumps of 6 on the number line and end up at 24.
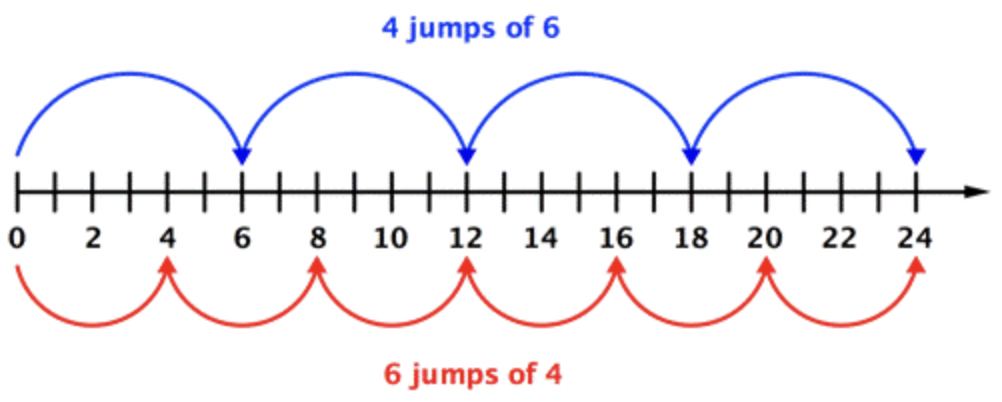
Or, you could make 6 rows of 4 or 4 rows of 6 and still have 24 squares.
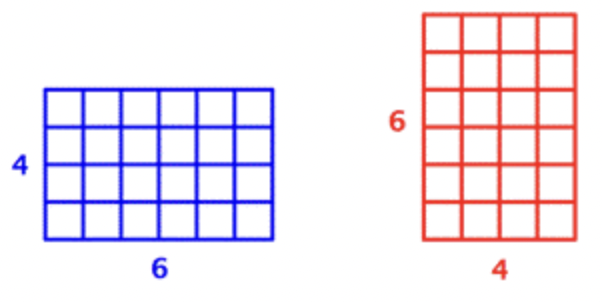
\(\ 6 \cdot 4=24\) and \(\ 4 \cdot 6=24\).
Tanisha modeled \(\ 5 \cdot 8\) using the following models. Which models are accurate representations of the multiplication of these two factors?
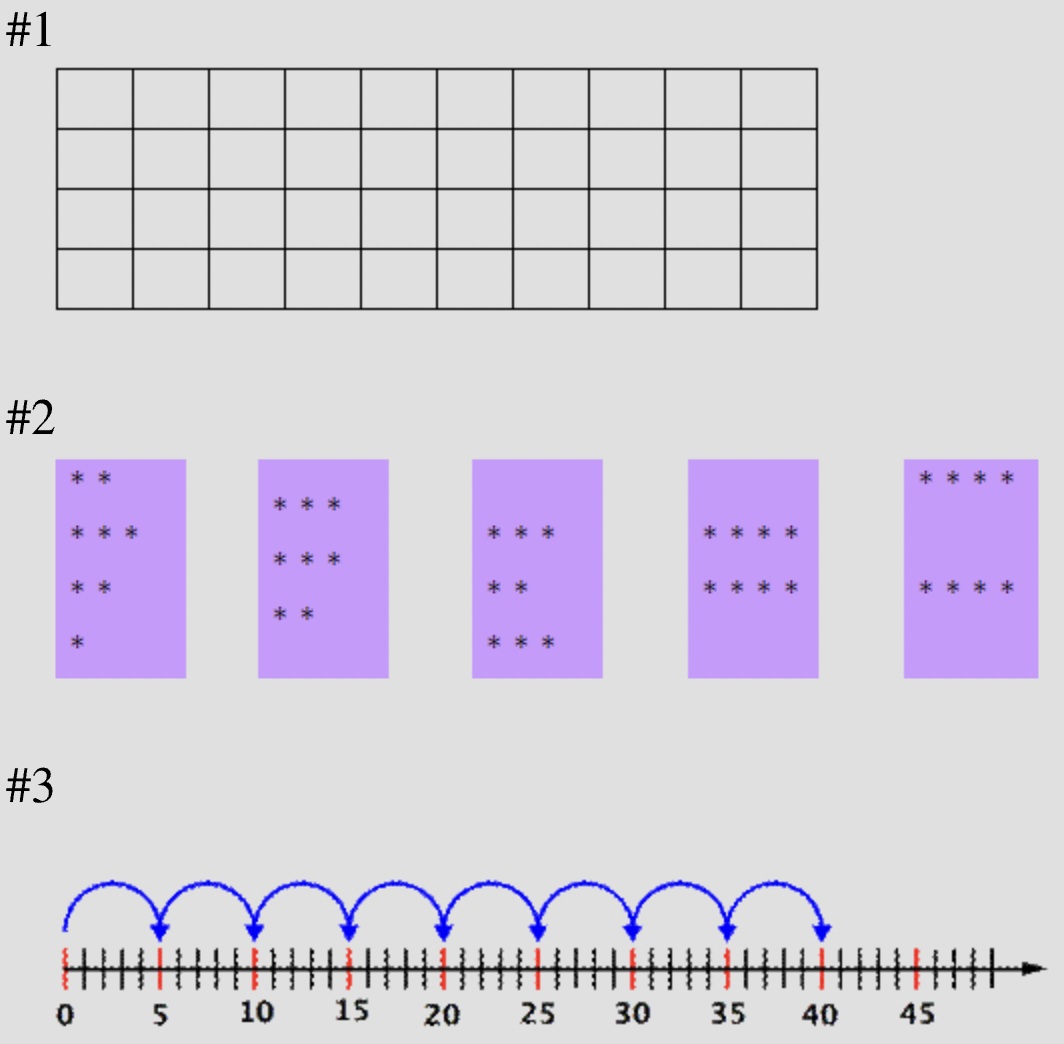
- All three models accurately represent \(\ 5 \cdot 8\).
- Only models #1 and #3 accurately represent \(\ 5 \cdot 8\).
- Only models #2 and #3 accurately represent \(\ 5 \cdot 8\).
- None of the models accurately represents \(\ 5 \cdot 8\).
- Answer
-
- All three models accurately represent \(\ 5 \cdot 8\). Incorrect. While the first model has the same product, it models the factors \(\ 4 \cdot 10\). The correct answer is Only models #2 and #3 accurately represent \(\ 5 \cdot 8\).
- Only models #1 and #3 accurately represent \(\ 5 \cdot 8\). Incorrect. Model #1 models \(\ 4 \cdot 10\), not \(\ 5 \cdot 8\). The correct answer is Only models #2 and #3 accurately represent \(\ 5 \cdot 8\).
- Only models #2 and #3 accurately represent \(\ 5 \cdot 8\). Correct. Model #2 shows 5 groups of 8, which equals 40. Model #3 shows skip counting 8 times by 5 to get to 40.
- None of the models accurately represents \(\ 5 \cdot 8\). Incorrect. Models #2 and #3 represent the multiplication \(\ 5 \cdot 8\). The correct answer is Only models #2 and #3 accurately represent \(\ 5 \cdot 8\).
Multiplying Greater Numbers
Let’s go back to the question posed at the opening of this topic of study. How can you use multiplication to figure out the total cost of 6 baseball caps that cost $14 each? (You do not have to pay sales tax). You can figure out the cost by multiplying \(\ 14 \cdot 6\).
One way to do this computation is to break 14 down into parts and multiply each part by 6.
\(\ \begin{aligned}
14 &=10+4 \quad \text { So, } \\
14 \cdot 6 &=10 \cdot 6+4 \cdot 6 \\
&=60+24 \\
&=84
\end{aligned}\)
You may recall the multiplication computed as \(\ 14 \cdot 6\):
\(\ \begin{array}{r}
2 \\
14 \\
\times \quad 6 \\
\hline 84
\end{array}\)
In this notation, some of the steps are written down with special notation. The product of 6 and 4(24) is written by putting the 4 in the ones place and writing a 2 up above the 1. This 2 actually stands for 20. Then, 6 is multiplied by 1. We are actually multiplying 6 by 1 ten and adding 20 to get the 80 in 84.
An example of multiplying two two-digit numbers is shown below. When performing this multiplication, each part of each number is multiplied by the other number. The numeric notation and an accompanying description are provided.
\(\ 47 \cdot 52\)
Solution
| \(\ \begin{array}{r} 47 \\ \times\quad 52 \\ \hline \end{array}\) |
Stack the numbers with the place values aligned. |
| \(\ \begin{array}{r} \color{blue}1 \ \ \\ 4\color{red}7 \\ \times \quad 5\color{red}2 \\ \hline \color{blue}4 \end{array}\) |
Multiply the ones. \(\ 2 \times 7=14\) ones. Write 4 ones in the ones place and regroup 10 ones into the tens place. |
| \(\ \begin{array}{r} \color{red}1 \ \ \\ {\color{red}4}7 \\ \times \quad 5\color{red}2 \\ \hline {\color{blue}9}4 \end{array}\) |
Multiply 2 ones by 4 tens, and add the regrouped 1 ten. 2 ones times 4 tens + 1 ten = 9 tens |
| \(\ \begin{array}{r} \color{blue}3\ \ \ \ \\ 4\color{red}7 \\ \times \quad {\color{red}5}2 \\ \hline 94 \\ \color{blue}50 \end{array}\) |
Multiply the tens. \(\ 5 \times 7=35\) tens. Write 5 tens in the tens place and regroup. |
| \(\ \begin{array}{r} \color{blue}3\ \ \ \ \\ {\color{red}4}7 \\ \times {\color{red}5}2 \\ \hline 94 \\ {\color{blue}23}50 \end{array}\) |
Multiply: 5 tens times 4 tens = 20 hundreds. Add the regrouped 3, which is 3 hundred. |
| \(\ \begin{array}{r} 3\ \ \ \ \\ {\color{red}4}7 \\ \times\quad {\color{red}5}2 \\ \hline \color{blue}1\color{red}94 \\ \color{red}2350 \\ \hline \color{blue}2,444 \end{array}\) |
Add the two lines. 94+2,350 |
\(\ 47 \cdot 52=2,444\)
Notice that you are multiplying each of the parts of each number by the parts of the other number. You are doing so in a systematic way, from ones places to tens places. You are also using notation to keep track of what you have regrouped. These are shown with raised numbers.
To keep your columns straight and your work organized, consider using grid paper or lined paper turned sideways so the lines form columns. Here is an example of a problem written on grid paper:
\(\ \begin{array}{|l|l|l|l|}
\hline & & 2 & 3 \\
\hline & \mathrm{x} & 1 & 2 \\
\hline & & \color{blue}4 & \color{blue}6 \\
\hline+ & \color{blue}2 & \color{blue}3 & \color{blue}0 \\
\hline & \color{red}2 & \color{red}7 & \color{red}6 \\
\hline
\end{array}\)
When you are multiplying whole numbers, be sure to line up the digits by their place values. In the example above, the digits in the ones place are lined up: the 2 in 12 is directly below the 3 in 23.
Multiplying Whole Numbers by 10
When you multiply numbers by 10 or powers of 10(100 ; 1,000 ; 10,000 ; 100,000), you’ll discover some interesting patterns. These patterns occur because our number system is based on ten: ten ones equal ten; ten tens equal one hundred; ten hundreds equal one thousand. Learning about these patterns can help you compute easily and quickly.
Consider the example of \(\ 25 \cdot 100\). First, let’s use the standard algorithm method to multiply these numbers.
\(\ 25 \cdot 100\)
Solution
\(\ \begin{array}{r}
100 \\
\times \quad 25 \\
\hline 500 \\
2000 \\
\hline 2,500
\end{array}\)
\(\ 25 \cdot 100=2,500\)
Using the standard algorithm, we calculated \(\ 25 \cdot 100=2,500\).
Look at the table below to find a pattern in the factors and products. See how the number of zeros in the power of 10(10,100, 1,000, etc.) relates to the number of zeros in the product.
| Factors | Product |
| \(\ 5 \cdot 10\) | = 50 |
| \(\ 5 \cdot 100\) | = 500 |
| \(\ 5 \cdot 1,000\) | = 5,000 |
| \(\ 5 \cdot 10,000\) | = 50,000 |
You can see that the number of zeros in the product matches the number of zeros in the power of 10(10,100,1,000, etc.). Will this always be true or is it true only in certain situations? Look at two more patterns:
| Factors | Product |
| \(\ 10 \cdot 10\) | = 100 |
| \(\ 10 \cdot 100\) | = 1,000 |
| \(\ 10 \cdot 1,000\) | = 10,000 |
| \(\ 10 \cdot 10,000\) | = 100,000 |
| Factors | Product |
| \(\ 120 \cdot 10\) | = 1,200 |
| \(\ 120 \cdot 100\) | = 12,000 |
| \(\ 120 \cdot 1,000\) | = 120,000 |
| \(\ 120 \cdot 10,000\) | = 1,200,000 |
Notice that in these last two examples, both factors had zeros in them. The number of zeros in the product is equal to the sum of the number of zeros at the end of each of the factors.
The example below illustrates how to multiply \(\ 140 \cdot 3000\).
\(\ 140 \cdot 3000\)
Solution
| \(\ \begin{array}{r} \color{blue}1 \ \ \\ 14 \\ \times \quad 3 \\ \hline \color{blue}42 \end{array}\) |
Identify the non-zero parts of the factors and multiply these parts. Multiply 3 ones by 4 ones. \(\ 4 \cdot 3=12\). |
| 420,000 |
Count the number of zeros in each factor. 140 has one zero; 3,000 has three zeros. 1+3=4 Write another 4 zeros after the 42. |
\(\ 140 \cdot 3000=420,000\)
When you multiply a whole number by 10 or a power of 10, first multiply the nonzero parts of the numbers. Then include the number of zeros at the end of the product equal to the total number of zeros at the end of the factors.
\(\ 13 \cdot 100=1,300\)
\(\ 180 \cdot 2,000=360,000\)
An apple orchard sold 100 bags of apples. If there are 30 apples in each bag, how many apples did the orchard sell?
- 130
- 300
- 30,000
- 3,000
- Answer
-
- Incorrect. You need to multiply 100 and 30, not add. The correct answer is 3,000.
- Incorrect. \(\ 30 \cdot 100=3,000\). You did not include the correct number of zeros. The correct answer is 3,000.
- Incorrect. \(\ 30 \cdot 100=3,000\). You included too many zeros. The correct answer is 3,000.
- Correct. \(\ 30 \cdot 100=3,000.3 \cdot 1=3\) and add three zeros since there is one zero in 30 and there are two zeros in 100.
Using Rounding to Estimate Products
Sometimes you don’t need an exact product because an estimate is enough. If you’re shopping, stopping to make a calculation with pencil and paper, or even a calculator, is inconvenient. Usually, shoppers will round numbers up so they will be sure that they have enough money for their purchases.
Estimating products is also helpful for checking an answer to a multiplication problem. If your actual calculation is quite different from your estimate, there is a good chance you have made a place value and/or regrouping mistake.
To estimate a product, you often round the numbers first. When you round numbers, you are always rounding to a particular place value, such as the nearest thousand or the nearest ten. If you are rounding a number to the nearest ten, you round it to the ten that is closest to the original number. An example of this is rounding 317 to the nearest ten. In this case, you round 317 to 320. If the number is half way in between (315), generally round up to 320.
Rounding factors can make it easy to multiply in your head. Let’s consider the multiplication problem \(\ 145 \cdot 29\). To estimate this product by rounding, you can round to the nearest ten.
Use rounding to estimate the product of \(\ 145 \cdot 29\).
Solution
| \(\ 150 \cdot 30\) | Round numbers to the nearest ten. |
| \(\ 15 \cdot 3=45\) | Multiply the non-zero numbers. |
| 4,500 | Count the zeros in the factors and include that many zeros after the 45. |
The estimate of \(\ 145 \cdot 29 \text { is } 4,500\).
You can use a calculator to see if your estimate seems reasonable. Or you can use estimation to make sure that the answer that you got on a calculator is reasonable. (Have you ever input the wrong numbers?)
|
Key entries: 145 x 29 = Result: 4,205 The exact product and the estimate are close enough to give you confidence in your calculations. |
A factory produces 58 packages of cookies in one hour. There are 32 cookies in each package. Which is the best estimate of the number of cookies the factory produces in one hour?
- 1,800
- 1,500
- 18,000
- 180
- Answer
-
- Correct. Multiplying \(\ 60 \cdot 30\) would give a good estimate. \(\ 60 \cdot 30=1,800\).
- Incorrect. \(\ 50 \cdot 30=1,500\), but 58 rounds to 60, not 50.The correct answer is 1,800.
- Incorrect. \(\ 60 \cdot 30=1,800\). The correct answer is 1,800.
- Incorrect. \(\ 60 \cdot 30=1,800\). The correct answer is 1,800.
Finding the Area of a Rectangle
The formula for the area of a rectangle uses multiplication: \(\ \text { length } \cdot \text { width }=\text { area }\). Applying what you know about multiplication, you can find the area of any rectangle if you know its dimensions (length and width). Consider the rectangle that is 4 by 7 shown below. Its length is 7 and its width is 4.
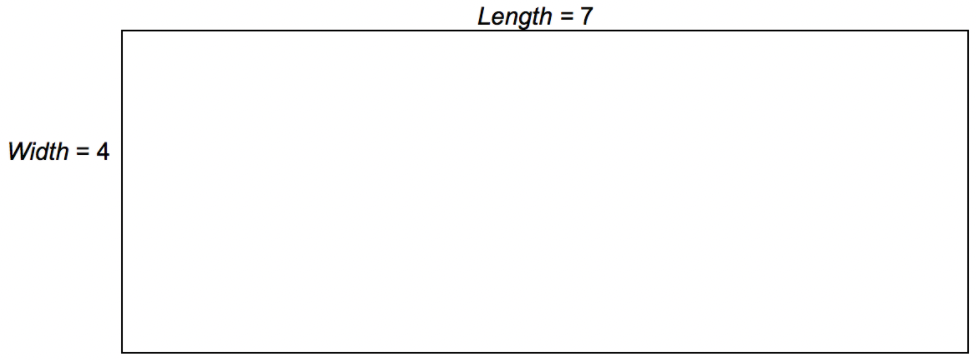
You can divide the rectangle into units by making 7 columns and 4 rows.
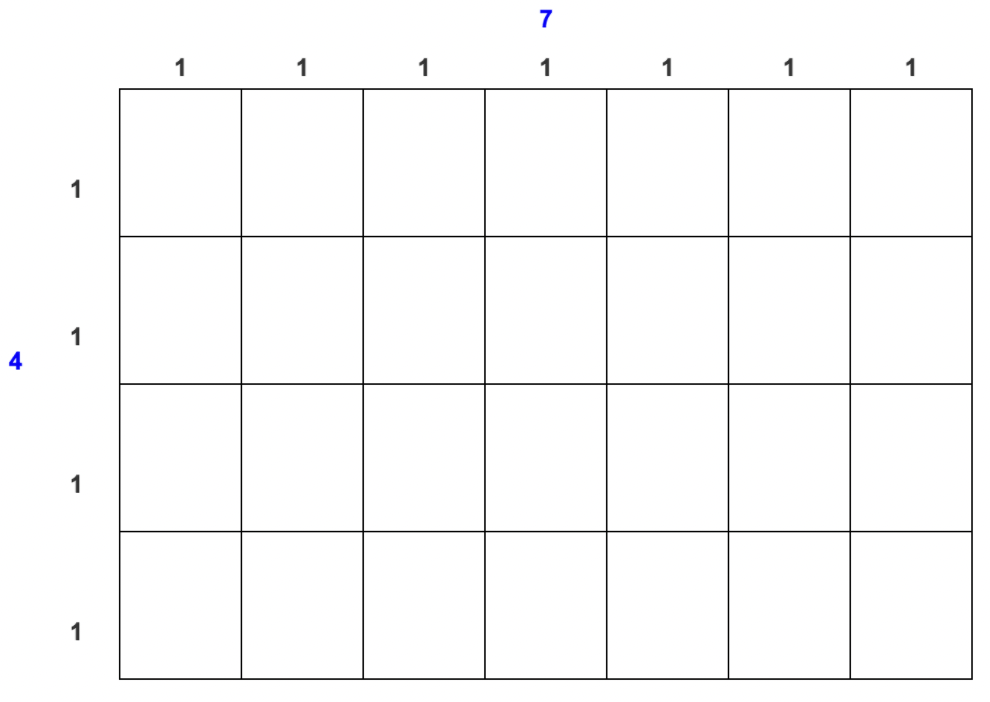
You can see that dividing the rectangle in this way results in 28 squares. You could say that the area of the rectangle is 28 square units. You could also find the area by multiplying \(\ 7 \cdot 4\). (Note: Area is always measured in square units: square inches, square centimeters, square feet, etc.)
Consider an example of a larger rectangle, like one that is found on a soccer field. At each end of a soccer field, centered at the goal, is a large rectangle. This rectangle is called the penalty box because fouls committed within the lines of this rectangle may result in a penalty kick. On a regulation soccer field, the penalty box is 44 yards by 18 yards. What is the area of a penalty box?
\(\ 44 \text { yards } \cdot 18 \text { yards }\)
Solution
\(\ \begin{array}{r}
3\ \ \ \ \\
44 \\
\times \quad 18 \\
\hline 352 \\
+\quad 440 \\
\hline 792
\end{array}\)
The area of the penalty box is 792 square yards.
What is the area of a rectangle whose length is 23 feet and whose width is 7 feet?
- 30 feet
- 161 feet
- 161 square feet
- 1,421 square feet
- Answer
-
- Incorrect. To find the area, you multiply, not add, the length and width. The correct answer is 161 square feet.
- Incorrect. Area is measured in square units. The correct answer is 161 square feet.
- Correct. \(\ 23 \cdot 7=161\)
- Incorrect. There is a place-value mistake. When you multiply \(\ 7 \cdot 3\), you need to regroup 20 ones to 2 tens and add it to the product of 2 and 7. The correct answer is 161 square feet.
Using Multiplication in Problem Solving
Multiplication is used in solving many types of problems. Below are two examples that use multiplication in their solutions to the problem.
A case of cat food has two layers. Each layer has 4 rows of 6 cans. How many cans are in a case of cat food?
Solution
| \(\ \begin{array}{r} 6 \\ \times \quad 4 \\ \hline 24 \end{array}\) |
First find the number of cans in one layer. You can multiply to figure this out. |
| \(\ \begin{array}{r} 24 \\ \times \quad 2 \\ \hline 48 \end{array}\) |
Since there are two layers, you multiply the number of cans in one layer by 2. |
There are 48 cans in a case of cat food.
A theater has 45 rows with 40 seats in each row. How many seats are there in the theater?
Solution
| \(\ \begin{array}{rr} &&\color{blue}2 \ \ \ \ \\ &&45 \\ &\times\quad &40 \\ \hline &&\color{blue}00 \\ &\color{blue}+ \quad&\color{blue}1800 \\ \hline &&\color{blue}1,800 \end{array}\) |
You can solve this problem by adding 40, 45 times, but that would take a lot of work. Multiplication is the way to go. |
There are 1,800 seats in the theater.
A lawn care company charges $35 to mow a lawn. If the company mows 32 lawns, how much money will it make?
- $9,760
- $1,120
- $130.00
- $67.00
- Answer
-
- Incorrect. This answer is too large. By estimation, \(\ 40 \cdot 30=1200\). There must be an error in regrouping or place value. The correct answer is $1,120.
- Correct. \(\ 35 \cdot 32=1,200\)
- Incorrect. The answer should be a larger number. By estimation, \(\ 40 \cdot 30=1200\). There must be an error in regrouping or place value. The correct answer is $1,120.
- Incorrect. You must multiply, not add, 32 and 35. The correct answer is $1,120.
Summary
Multiplication can make repeated addition easier to compute in calculations and problem solving. Multiplication can be written using three symbols: parentheses, a times sign, or a multiplication dot. To perform multiplication with two-digit factors or greater, you can use the standard algorithm where you multiply each of the numbers in each factor by the numbers in the other factor. Using strategies such as short cuts for multiplying by powers of 10 and estimation to check your answers can make multiplication easier as well as reduce errors.


