10.2.1.4: Simplifying Fractions

Last updated
Save as PDF

Page ID: 113224

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Find an equivalent fraction with a given denominator.
Simplify a fraction to lowest terms.

Introduction

Fractions are used to represent a part of a whole. Fractions that represent the same part of a whole are called equivalent fractions. Factoring, multiplication, and division are all helpful tools for working with equivalent fractions.

Equivalent Fractions

We use equivalent fractions every day. Fifty cents can be 2 quarters, and we have $\ \frac{2}{4}$ of a dollar, because there are 4 quarters in a dollar. Fifty cents is also 50 pennies out of 100 pennies, or $\ \frac{50}{100}$ of a dollar. Both of these fractions are the same amount of money, but written with a different numerator and denominator.

Think about a box of crackers that contains 3 packets of crackers. Two of these packets are $\ \frac{2}{3}$ of the box. Suppose each packet has 30 crackers in it. Two packets are also $\ 60(30 \cdot 2)$ crackers out of $\ 90(30 \cdot 3)$ crackers. This is $\ \frac{60}{90}$ of the box. The fractions $\ \frac{2}{3}$ and $\ \frac{60}{90}$ both represent two packets of crackers, so they are equivalent fractions.

Equivalent fractions represent the same part of a whole, even if the numerator and denominator are different. For example, $\ \frac{1}{4}=\frac{5}{20}$. In these diagrams, both fractions represent one of four rows in the rectangle.

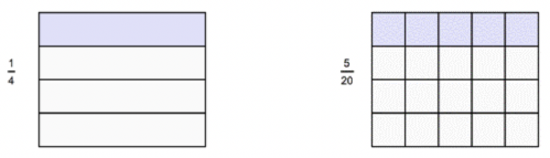
$Screen Shot 2021-04-20 at 1.42.47 PM.png$

Since $\ \frac{1}{4}$ and $\ \frac{5}{20}$ are naming the same part of a whole, they are equivalent.

There are many ways to name the same part of a whole using equivalent fractions.

Let’s look at an example where you need to find an equivalent fraction.

Example

John is making cookies for a bake sale. He made 20 large cookies, but he wants to give away only $\ \frac{3}{4}$ of them for the bake sale. What fraction of the cookies does he give away, using 20 as the denominator?

Solution

$Screen Shot 2021-04-20 at 1.png$

Start with 20 cookies.

$Screen Shot 2021-04-20 at 1.png$

Because the denominator of $\ \frac{3}{4}$ is 4, make 4 groups of cookies, 5 in each group.

$Screen Shot 2021-04-20 at 1.png$

$\ \frac{3}{4}=\frac{3 \cdot 5}{4 \cdot 5}$ because there are 5 cookies in each group.

$\ \frac{3}{4}=\frac{3 \cdot 5}{4 \cdot 5}=\frac{15}{20}$

He gives away $\ \frac{15}{20}$ of the cookies.

When you regroup and reconsider the parts and whole, you are multiplying the numerator and denominator by the same number. In the above example, you multiply 4 by 5 to get the needed denominator of 20, so you also need to multiply the numerator 3 by 5, giving the new numerator of 15.

Finding Equivalent Fractions

To find equivalent fractions, multiply or divide both the numerator and the denominator by the same number.

Examples:

$\ \frac{20}{25}=\frac{20 \div 5}{25 \div 5}=\frac{4}{5}$

$\ \frac{2}{7}=\frac{2 \cdot 6}{7 \cdot 6}=\frac{12}{42}$

Exercise

Write an equivalent fraction to $\ \frac{2}{3}$ that has a denominator of 27.

$\ \frac{26}{27}$
$\ \frac{11}{27}$
$\ \frac{18}{27}$
$\ \frac{12}{18}$

Answer

Incorrect. You may have added the difference between the two denominators to the numerator (27-3=24, 24+2=26). Instead, you need to use a multiplying factor of $\ 9(27 \div 3)$. The correct answer is $\ \frac{18}{27}$.
Incorrect. You may have added the multiplying factor of 9 to the numerator. Instead, multiply the numerator by this factor. The correct answer is $\ \frac{18}{27}$.
Correct. The multiplying factor is 9, so the denominator is $\ 3 \cdot 9=27$ and the numerator is $\ 2 \cdot 9=18$.
Incorrect. Although this is an equivalent fraction to $\ \frac{2}{3}$, the denominator is not 27. The correct answer is $\ \frac{18}{27}$.

Simplifying Fractions

A fraction is in its simplest form, or lowest terms, when it has the least numerator and the least denominator possible for naming this part of a whole. The numerator and denominator have no common factor other than 1.

Here are 10 blocks, 4 of which are green. So, the fraction that is green is $\ \frac{4}{10}$. To simplify, you find a common factor and then regroup the blocks by that factor.

Example

Simplify $\ \frac{4}{10}$.

Solution

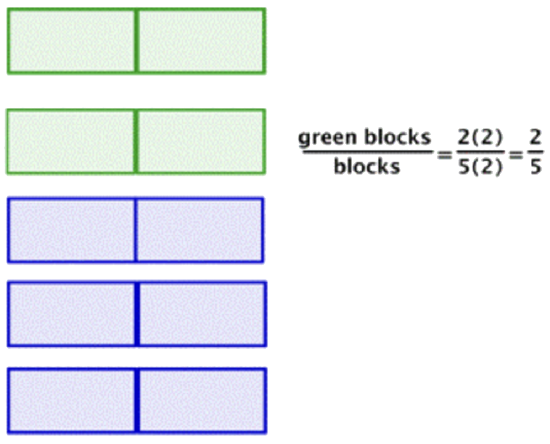$Screen Shot 2021-04-20 at 2.png$	We start with 4 green blocks out of 10 total blocks.
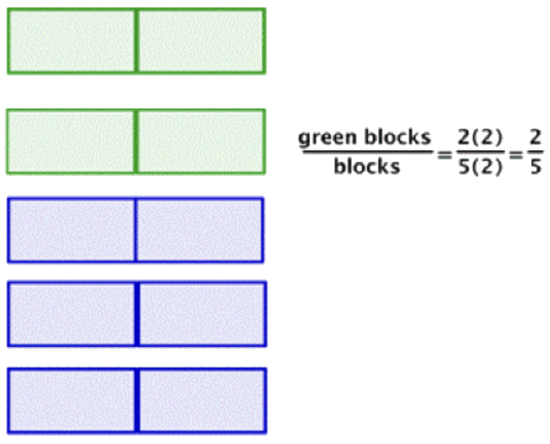$Screen Shot 2021-04-20 at 2.png$	Group the blocks in twos, since 2 is a common factor. You have 2 groups of green blocks and a total of 5 groups, each group containing 2 blocks.
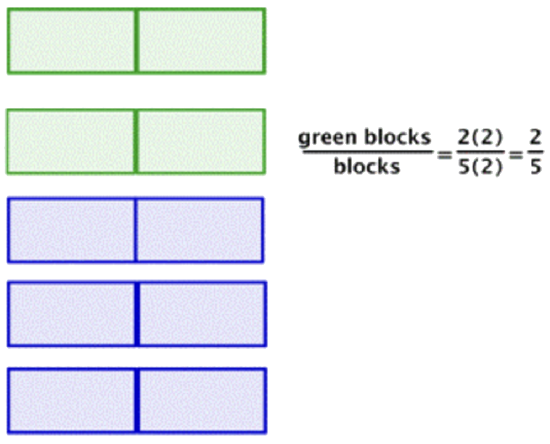$Screen Shot 2021-04-20 at 2.png$	Now, consider the groups as the part and you have 2 green groups out of 5 total groups.

$\ \frac{4}{10}=\frac{2}{5}$ The simplified fraction is $\ \frac{2}{5}$.

Once you have determined a common factor, you can divide the blocks into the groups by dividing both the numerator and denominator to determine the number of groups that you have.

For example, to simplify $\ \frac{6}{9}$ you find a common factor of 3, which will divide evenly into both 6 and 9. So, you divide 6 and 9 into groups of 3 to determine how many groups of 3 they contain. This gives $\ \frac{6 \div 3}{9 \div 3}=\frac{2}{3}$, which means 2 out of 3 groups, and $\ \frac{2}{3}$ is equivalent to $\ \frac{6}{9}$.

It may be necessary to group more than one time. Each time, determine a common factor for the numerator and denominator using the tests of divisibility, when possible. If both numbers are even numbers, start with 2. For example:

Example

Simplify $\ \frac{32}{48}$.

Solution

$\ \frac{32}{48}=\frac{32 \div 2}{48 \div 2}=\frac{16}{24}$	32 and 48 have a common factor of 2. Divide each by 2.
$\ \frac{16}{24}=\frac{16 \div 2}{24 \div 2}=\frac{8}{12}$	16 and 24 have a common factor of 2. Divide each by 2.
$\ \frac{8}{12}=\frac{8 \div 4}{12 \div 4}=\frac{2}{3}$	8 and 12 have a common factor of 4. Divide each by 4.
$\ \frac{32}{48}=\frac{2}{3}$	$\ \frac{2}{3}$ is the simplified fraction equivalent to $\ \frac{32}{48}$.

In the example above, 16 is a factor of both 32 and 48, so you could have shortened the solution.

$\ \frac{32}{48}=\frac{2 \cdot 16}{3 \cdot 16}=\frac{2}{3}$

You can also use prime factorization to help regroup the numerator and denominator.

Example

Simplify $\ \frac{54}{72}$.

Solution

$\ \frac{54}{72}=\frac{2 \cdot 3 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}$	The prime factorization of 54 is $\ 2 \cdot 3 \cdot 3 \cdot 3$. The prime factorization of 72 is $\ 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3$.
$\ \frac{3 \cdot(2 \cdot 3 \cdot 3)}{2 \cdot 2 \cdot(2 \cdot 3 \cdot 3)}$	Rewrite, finding common factors.
$\ \frac{3}{2 \cdot 2} \cdot 1$	$\ \frac{2 \cdot 3 \cdot 3}{2 \cdot 3 \cdot 3}=1$
$\ \frac{3}{4}$	Multiply: $\ 2 \cdot 2$.
$\ \frac{54}{72}=\frac{3}{4}$	$\ \frac{3}{4}$ is the simplified fraction equivalent to $\ \frac{54}{72}$.

Notice that when you simplify a fraction, you divide the numerator and denominator by the same number, in the same way you multiply by the same number to find an equivalent fraction with a greater denominator. In the example above, you could have divided the numerator and denominator by 9, a common factor of 54 and 72.

$\ \frac{54 \div 9}{72 \div 9}=\frac{6}{8}$

Since the numerator (6) and the denominator (8) still have a common factor, the fraction is not yet in lowest terms. So, again divide by the common factor 2.

$\ \frac{6 \div 2}{8 \div 2}=\frac{3}{4}$

Repeat this process of dividing by a common factor until the only common factor is 1.

Simplifying Fractions to Lowest Terms

To simplify a fraction to lowest terms, divide both the numerator and the denominator by their common factors. Repeat as needed until the only common factor is 1.

Exercise

Simplify $\ \frac{36}{72}$.

$\ \frac{3}{6}$
$\ \frac{9}{18}$
$\ \frac{18}{38}$
$\ \frac{1}{2}$

Answer

Incorrect. Although $\ \frac{3}{6}$ is an equivalent fraction to $\ \frac{36}{72}$, it is not in lowest terms. There is a common factor of 3 in the numerator and denominator. The correct answer is $\ \frac{1}{2}$.
Incorrect. Although $\ \frac{9}{18}$ is an equivalent fraction to $\ \frac{36}{72}$, it is not in lowest terms. There are other common factors (9 and 3). The correct answer is $\ \frac{1}{2}$.
Incorrect. You may have divided 72 by 2 and got 38 rather than 36. $\ \frac{18}{36}$ is an equivalent fraction to $\ \frac{36}{72}$, but it is not in lowest terms. The correct answer is $\ \frac{1}{2}$.
Correct. $\ \frac{1}{2}$ is in lowest terms, as 1 is the only common factor of 1 and 2.

Summary

Equivalent fractions do not always have the same numerator and denominator, but they have the same value. A fraction is in lowest terms when the numerator and denominator of the fraction share no common factors other than . A fraction written in lowest terms is called a simplified fraction.

\(\ \frac{32}{48}=\frac{32 \div 2}{48 \div 2}=\frac{16}{24}\)	32 and 48 have a common factor of 2. Divide each by 2.
\(\ \frac{16}{24}=\frac{16 \div 2}{24 \div 2}=\frac{8}{12}\)	16 and 24 have a common factor of 2. Divide each by 2.
\(\ \frac{8}{12}=\frac{8 \div 4}{12 \div 4}=\frac{2}{3}\)	8 and 12 have a common factor of 4. Divide each by 4.
\(\ \frac{32}{48}=\frac{2}{3}\)	\(\ \frac{2}{3}\) is the simplified fraction equivalent to \(\ \frac{32}{48}\).

\(\ \frac{54}{72}=\frac{2 \cdot 3 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}\)	The prime factorization of 54 is \(\ 2 \cdot 3 \cdot 3 \cdot 3\). The prime factorization of 72 is \(\ 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\).
\(\ \frac{3 \cdot(2 \cdot 3 \cdot 3)}{2 \cdot 2 \cdot(2 \cdot 3 \cdot 3)}\)	Rewrite, finding common factors.
\(\ \frac{3}{2 \cdot 2} \cdot 1\)	\(\ \frac{2 \cdot 3 \cdot 3}{2 \cdot 3 \cdot 3}=1\)
\(\ \frac{3}{4}\)	Multiply: \(\ 2 \cdot 2\).
\(\ \frac{54}{72}=\frac{3}{4}\)	\(\ \frac{3}{4}\) is the simplified fraction equivalent to \(\ \frac{54}{72}\).