10.2.1.5: Comparing Fractions

Last updated
Save as PDF

Page ID: 113225

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Determine whether two fractions are equivalent.
Use > or < to compare fractions.

Introduction

You often need to know when one fraction is greater or less than another fraction. Since a fraction is a part of a whole, to find the greater fraction you need to find the fraction that contains more of the whole. If the two fractions simplify to fractions with a common denominator, you can then compare numerators. If the denominators are different, you can find a common denominator first and then compare the numerators.

Determining Equivalent Fractions

Two fractions are equivalent fractions when they represent the same part of a whole. Since equivalent fractions do not always have the same numerator and denominator, one way to determine if two fractions are equivalent is to find a common denominator and rewrite each fraction with that denominator. Once the two fractions have the same denominator, you can check to see if the numerators are equal. If they are equal, then the two fractions are equal as well.

One way to find a common denominator is to check to see if one denominator is a factor of the other denominator. If so, the greater denominator can be used as the common denominator.

Example

Are $\ \frac{2}{6}$ and $\ \frac{8}{18}$ equivalent fractions?

Solution

Does $\ \frac{2}{6}=\frac{8}{18} ?$	To solve this problem, find a common denominator for the two fractions. This will help you compare the two fractions. Since 6 is a factor of 18, you can write both fractions with 18 as the denominator.
$\ \frac{2 \cdot 3}{6 \cdot 3}=\frac{6}{18}$	Start with the fraction $\ \frac{2}{6}$. Multiply the denominator, 6, by 3 to get a new denominator of 18. Since you multiply the denominator by 3, you must also multiply the numerator by 3.
$\ \frac{8}{18}$	The fraction $\ \frac{8}{18}$ already has a denominator of 18, so you can leave it as is.
$\ \frac{6}{18}$ does not equal $\ \frac{8}{18}$	Compare the fractions. Now that both fractions have the same denominator, 18, you can compare numerators.

$\ \frac{2}{6}$ and $\ \frac{8}{18}$ are not equivalent fractions.

When one denominator is not a factor of the other denominator, you can find a common denominator by multiplying the denominators together.

Example

Determine whether $\ \frac{3}{6}$ and $\ \frac{5}{10}$ are equivalent fractions.

Solution

$\ 6 \cdot 10=60$	Use 60 as a common denominator.
$\ \frac{3}{6}=\frac{3 \cdot 10}{6 \cdot 10}=\frac{30}{60}$	Multiply the numerator and denominator of $\ \frac{3}{6}$ by 10 to get 60 in the denominator.
$\ \frac{5}{10}=\frac{5.6}{10 \cdot 6}=\frac{30}{60}$	Multiply the numerator and denominator of $\ \frac{5}{10}$ by 6.
$\ \frac{30}{60}=\frac{30}{60}$	Now that the denominators are the same, compare the numerators.
Yes, $\ \frac{3}{6}$ and $\ \frac{5}{10}$ are equivalent fractions.	Since 30 is the value of the numerator for both fractions, the two fractions are equal.

Notice in the above example that you can use 30 as the least common denominator since both 6 and 10 are factors of 30. Any common denominator will work.

In some cases, you can simplify one or both of the fractions, which can result in a common denominator.

Example

Determine whether $\ \frac{2}{3}$ and $\ \frac{40}{60}$ are equivalent fractions.

Solution

$\ \frac{40}{60}=\frac{40 \div 10}{60 \div 10}=\frac{4}{6}$

Simplify $\ \frac{40}{60}$.

Divide the numerator and denominator by the common factor 10.

$\ \frac{4}{6}=\frac{4 \div 2}{6 \div 2}=\frac{2}{3}$

$\ \frac{4}{6}$ is still not in lowest terms, so divide the numerator and the denominator again, this time by the common factor 2.

$\ \frac{2}{3}=\frac{2}{3}$

Compare the fractions. The numerators and denominators are the same.

Yes, $\ \frac{2}{3}$ and $\ \frac{40}{60}$ are equivalent fractions.

Note

In the example above, you could have used the common factor of 20 to simplify $\ \frac{40}{60}$ directly to $\ \frac{2}{3}$.

Determining Equivalent Fractions

To determine whether or not two fractions are equivalent:

Step 1: Rewrite one or both of the fractions so that they have common denominators.

Step 2: Compare the numerators to see if they have the same value. If so, then the fractions are equivalent.

Exercise

Which of the following fraction pairs are equivalent?

$\ \frac{5}{7}$ and $\ \frac{7}{5}$
$\ \frac{12}{30}$ and $\ \frac{6}{10}$
$\ \frac{4}{20}$ and $\ \frac{1}{5}$
$\ \frac{8}{11}$ and $\ \frac{8}{22}$

Answer

Incorrect. Although the same numbers, 5 and 7, are used in each fraction, the numerators and denominators are not equal, so the fractions cannot be equivalent. The correct answer is $\ \frac{4}{20}$ and $\ \frac{1}{5}$.
Incorrect. 30 is divisible by 10, and 12 is divisible by 6. However, they do not share a common multiple: $\ 6 \cdot 2=12$, and $\ 10 \cdot 3=30$. This means the fractions are not equivalent. The correct answer is $\ \frac{4}{20}$ and $\ \frac{1}{5}$.
Correct. Take the fraction $\ \frac{1}{5}$ and multiply both the numerator and denominator by 4. You are left with the fraction $\ \frac{4}{20}$. This means that the two fractions are equivalent.
Incorrect. The numerators of the two fractions are the same, but the denominators are different. This means the fractions are not equivalent. The correct answer is $\ \frac{4}{20}$ and $\ \frac{1}{5}$

Comparing Fractions Using < and >

When given two or more fractions, it is often useful to know which fraction is greater than or less than the other. For example, if the discount in one store is $\ \frac{1}{3}$ off the original price and the discount in another store is $\ \frac{1}{4}$ off the original price, which store is offering a better deal? To answer this question, and others like it, you can compare fractions.

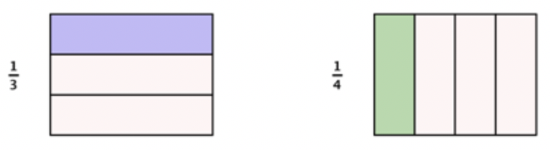
$Screen Shot 2021-04-21 at 12.07.37 PM.png$

To determine which fraction is greater, you need to find a common denominator. You can then compare the fractions directly. Since 3 and 4 are both factors of 12, you will divide the whole into 12 parts, create equivalent fractions for $\ \frac{1}{3}$ and $\ \frac{1}{4}$, and then compare.

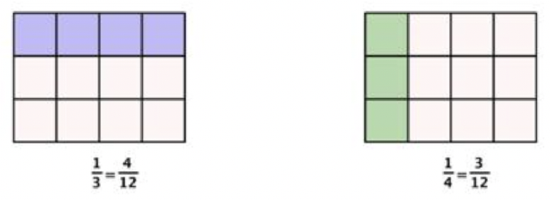
$Screen Shot 2021-04-21 at 12.12.42 PM.png$

Now you see that $\ \frac{1}{3}$ contains 4 parts of 12, and $\ \frac{1}{4}$ contains 3 parts of 12. So, $\ \frac{1}{3}$ is greater than $\ \frac{1}{4}$.

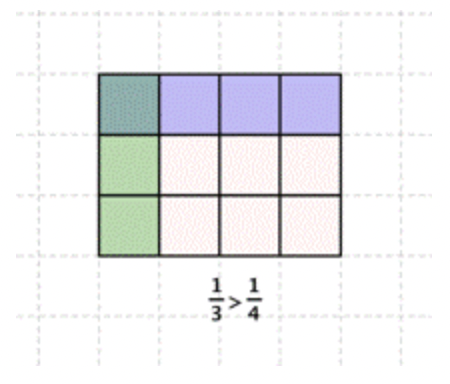
$Screen Shot 2021-04-21 at 10.06.04 PM.png$

As long as the denominators are the same, the fraction with the greater numerator is the greater fraction, as it contains more parts of the whole. The fraction with the lesser numerator is the lesser fraction, as it contains fewer parts of the whole.

Recall that the symbol < means “less than”, and the symbol > means “greater than”. These symbols are inequality symbols. So, the true statement 3<8 is read as "3 is less than 8" and the statement 5>3 is read as "5 is greater than 3". One way to help you remember the distinction between the two symbols is to think that the smaller end of the symbol points to the lesser number.

As with comparing whole numbers, the inequality symbols are used to show when one fraction is “greater than” or “less than” another fraction.

Comparing Fractions

To compare two fractions:

Step 1: Compare denominators. If they are different, rewrite one or both fractions with a common denominator.

Step 2: Check the numerators. If the denominators are the same, then the fraction with the greater numerator is the greater fraction. The fraction with the lesser numerator is the lesser fraction. And, as noted above, if the numerators are equal, the fractions are equivalent.

Example

Use < or > to compare the two fractions $\ \frac{4}{5}$ and $\ \frac{14}{20}$.

Solution

Is $\ \frac{4}{5}>\frac{14}{20}$ or is $\ \frac{4}{5}<\frac{14}{20}$?	You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the two fractions.
$\ \frac{4}{5}=\frac{?}{20}$	Since 5 is a factor of 20, you can use 20 as the common denominator.
$\ \frac{4 \cdot 4}{5 \cdot 4}=\frac{16}{20}$	Multiply the numerator and denominator by 4 to create an equivalent fraction with a denominator of 20.
$\ \frac{16}{20}>\frac{14}{20}$	Compare the two fractions. $\ \frac{16}{20}$ is greater than $\ \frac{14}{20}$.
$\ \frac{4}{5}>\frac{14}{20}$	If $\ \frac{16}{20}>\frac{14}{20}$, then $\ \frac{4}{5}>\frac{14}{20}$, since $\ \frac{4}{5}=\frac{16}{20}$.

Exercise

Which of the following is a true statement?

$\ \frac{5}{6}<\frac{24}{30}$
$\ \frac{75}{100}>\frac{9}{12}$
$\ \frac{4}{16}>\frac{1}{3}$
$\ \frac{3}{8}<\frac{20}{40}$

Answer

Incorrect. $\ \frac{5}{6}$ is equivalent to $\ \frac{25}{30}$, and since 25>24, $\ \frac{25}{30}>\frac{24}{30}$, which means $\ \frac{5}{6}>\frac{24}{30}$. The correct answer is $\ \frac{3}{8}<\frac{20}{40}$.
Incorrect. Both fractions simplify to $\ \frac{3}{4}$, so one isn’t greater than or less than the other one. They are equivalent. The correct answer is $\ \frac{3}{8}<\frac{20}{40}$.
Incorrect. Finding a common denominator, you can compare $\ \frac{12}{48}$ to $\ \frac{16}{48}$, and see that $\ \frac{12}{48}<\frac{16}{48}$, which means $\ \frac{4}{16}<\frac{1}{3}$. The correct answer is $\ \frac{3}{8}<\frac{20}{40}$.
Correct. Simplifying $\ \frac{20}{40}$, you get the equivalent fraction $\ \frac{1}{2}$. Since you still don’t have a common denominator, write $\ \frac{1}{2}$ as an equivalent fraction with a denominator of 8: $\ \frac{1}{2}=\frac{1 \cdot 4}{2 \cdot 4}=\frac{4}{8}$. You find that $\ \frac{3}{8}<\frac{4}{8}$, so $\ \frac{3}{8}<\frac{20}{40}$as well.

Summary

You can compare two fractions with like denominators by comparing their numerators. The fraction with the greater numerator is the greater fraction, as it contains more parts of the whole. The fraction with the lesser numerator is the lesser fraction as it contains fewer parts of the whole. If two fractions have the same denominator, then equal numerators indicate equivalent fractions.

Does \(\ \frac{2}{6}=\frac{8}{18} ?\)	To solve this problem, find a common denominator for the two fractions. This will help you compare the two fractions. Since 6 is a factor of 18, you can write both fractions with 18 as the denominator.
\(\ \frac{2 \cdot 3}{6 \cdot 3}=\frac{6}{18}\)	Start with the fraction \(\ \frac{2}{6}\). Multiply the denominator, 6, by 3 to get a new denominator of 18. Since you multiply the denominator by 3, you must also multiply the numerator by 3.
\(\ \frac{8}{18}\)	The fraction \(\ \frac{8}{18}\) already has a denominator of 18, so you can leave it as is.
\(\ \frac{6}{18}\) does not equal \(\ \frac{8}{18}\)	Compare the fractions. Now that both fractions have the same denominator, 18, you can compare numerators.

\(\ 6 \cdot 10=60\)	Use 60 as a common denominator.
\(\ \frac{3}{6}=\frac{3 \cdot 10}{6 \cdot 10}=\frac{30}{60}\)	Multiply the numerator and denominator of \(\ \frac{3}{6}\) by 10 to get 60 in the denominator.
\(\ \frac{5}{10}=\frac{5.6}{10 \cdot 6}=\frac{30}{60}\)	Multiply the numerator and denominator of \(\ \frac{5}{10}\) by 6.
\(\ \frac{30}{60}=\frac{30}{60}\)	Now that the denominators are the same, compare the numerators.
Yes, \(\ \frac{3}{6}\) and \(\ \frac{5}{10}\) are equivalent fractions.	Since 30 is the value of the numerator for both fractions, the two fractions are equal.

Is \(\ \frac{4}{5}>\frac{14}{20}\) or is \(\ \frac{4}{5}<\frac{14}{20}\)?	You cannot compare the fractions directly because they have different denominators. You need to find a common denominator for the two fractions.
\(\ \frac{4}{5}=\frac{?}{20}\)	Since 5 is a factor of 20, you can use 20 as the common denominator.
\(\ \frac{4 \cdot 4}{5 \cdot 4}=\frac{16}{20}\)	Multiply the numerator and denominator by 4 to create an equivalent fraction with a denominator of 20.
\(\ \frac{16}{20}>\frac{14}{20}\)	Compare the two fractions. \(\ \frac{16}{20}\) is greater than \(\ \frac{14}{20}\).
\(\ \frac{4}{5}>\frac{14}{20}\)	If \(\ \frac{16}{20}>\frac{14}{20}\), then \(\ \frac{4}{5}>\frac{14}{20}\), since \(\ \frac{4}{5}=\frac{16}{20}\).