10.3.1.1: Decimals and Fractions

Learning Objectives

• Read and write numbers in decimal notation.
• Write decimals as fractions.
• Write fractions as decimals.

Introduction

In addition to fraction notation, decimal notation is another way to write numbers between 0 and 1. Decimals can also be used to write numbers between any two whole numbers. For example, you may have to write a check for $2,003.38. Or, in measuring the length of a room, you may find that the length is between two whole numbers, such as 35.24 feet. In this topic, you will focus on reading and writing decimal numbers, and rewriting them in fraction notation.

To read or write numbers written in decimal notation, you need to know the place value of each digit, that is, the value of a digit based on its position within a number. With decimal numbers, the position of a numeral in relation to the decimal point determines its place value. For example, the place value of the 4 in 45.6 is in the tens place, while the place value of 6 in 45.6 is in the tenths place.

Decimal Notation

Decimal numbers are numbers whose place values are based on 10s. Whole numbers are actually decimal numbers that are greater than or equal to zero. The place-value chart can be extended to include numbers less than one, which are sometimes called decimal fractions. A decimal point is used to separate the whole number part of the number and the fraction part of the number.

Let’s say you are measuring the length of a driveway and find that it is 745 feet. You would say this number as seven hundred forty-five. Then, a more accurate measurement shows that it is 745.36 feet. Let’s place this number in a place-value chart.

What you want to examine now are the place values of the decimal part, which are the numbers 3 and 6 in the chart below.

Decimal Numbers	Hundreds	Tens	Ones	Decimal Point	Tenths	Hundredths
745.36	7	4	5	.	3	6

Notice how the place-value names start from the decimal point. To the left of the decimal point are the ones, tens, and hundreds places, where you put digits that represent whole numbers that are greater than or equal to zero. To the right of the decimal point are the tenths and hundredths, where you put digits that represent numbers that are fractional parts of one, numbers that are more than zero and less than one.

Again, the place value of a number depends on how far away it is from the decimal point. This is evident in the chart below, where each number has the digit "4" occupying a different place value.

Decimal Numbers	Thousands	Hundreds	Tens	Ones	Decimal Point	Tenths	Hundredths	Thousandths
0.004				0	.	0	0	4
0.04				0	.	0	4
0.4				0	.	4
4				4	.
40			4	0	.
400		4	0	0	.
4000	4	0	0	0	.

Imagine that as a large balloon deflates, the volume of air inside it goes from 1,000 liters, to 100 liters, to 10 liters, to 1 liter. Notice that you’re dividing a place value by ten as you go to the right. You divide 100 by 10 to get to the tens place. This is because there are 10 tens in 100. Then, you divide 10 by 10 to get to the ones place, because there are 10 ones in 10.

Now, suppose the balloon continues to lose volume, going from 1 liter, to 0.1 liters, to 0.01 liters, and then to 0.001 liters. Notice that you continue to divide by 10 when moving to decimals. You divide 1 by \(\ 10\left(\frac{1}{10}\right)\) to get to the tenths place, which is basically breaking one into 10 pieces. And to get to the hundreds place, you break the tenth into ten more pieces, which results in the fraction \(\ \frac{1}{100}\). The relationship between decimal places and fractions is captured in the table below.

Word Form	Decimal Notation	Fraction Notation
one thousand	1,000	\(\ \frac{1,000}{1}\)
one hundred	100	\(\ \frac{100}{1}\)
ten	10	\(\ \frac{10}{1}\)
one	1	\(\ \frac{1}{1}\)
one tenth	0.1	\(\ \frac{1}{10}\)
one hundredth	0.01	\(\ \frac{1}{100}\)
one thousandth	0.001	\(\ \frac{1}{1,000}\)

Consider a number with more digits. Suppose a fisherman has a net full of fish that weighs 1,357.924 kilograms. To write this number, you need to use the thousands place, which is made up of 10 hundreds. You also use the thousandths place, which is \(\ \frac{1}{10}\) of a hundredth. In other words, there are ten thousandths in one hundredth.

Decimal Numbers	no th side					th side
	Thousands	Hundreds	Tens	Ones	Decimal point	Tenths	Hundredths	Thousandths
1,357.924	1	3	5	7	.	9	2	4

As you can see, moving from the decimal point to the left is ones, tens, hundreds, thousands, etc. This is the “no th side,” which are the numbers greater than or equal to one. Moving from the decimal point to the right is tenths, hundredths, thousandths. This is the “th side,” which are the numbers less than 1.

1,357.924

no th side th side

The pattern going to the right or the left from the decimal point is the same, but there are two big differences:

1. The place values to the right of the decimal point all end in “th”.
2. There is no such thing as “one-ths.” From your work with fractions, you know that 5 and \(\ \frac{5}{1}\) are the same.

Example

What is the place value of 8 in 4,279.386?

Solution

Write the number in a place-value chart. Read the value of the 8 from the chart.

Decimal Numbers	no th side					th side
	Thousands	Hundreds	Tens	Ones	Decimal point	Tenths	Hundredths	Thousandths
4,279.386	4	2	7	9	.	3	8	6

In the number 4,279.386, the 8 is in the hundredths place.

Exercise

What is the place value of the 7 in 324.2671?

1. thousands
2. thousandths
3. hundreds
4. hundredths

Answer

1. Incorrect. The digit 7 is to the right of the decimal point, which means that it is less than one and on the th side. The correct answer is thousandths.
2. Correct. The digit 7 is three decimal places to the right of the decimal point, which means that it is in the thousandths place.
3. Incorrect. The digit 7 is three decimal places to the right of the decimal point, which means that it is in the thousandths place.
4. Incorrect. The digit 7 is three decimal places to the right of the decimal point, which means that it is in the thousandths place.

Reading Decimals

The easiest way to read a decimal number is to read the decimal fraction part as a fraction. (Don’t simplify the fraction though.) Suppose you have 0.4 grams of yogurt in a cup. You would say, "4 tenths of a gram of yogurt," as the 4 is in the tenths place.

Note that the denominator of the fraction written in fraction form is always a power of ten, and the number of zeros in the denominator is the same as the number of decimal places to the right of the decimal point. See the examples in the table below for further guidance.

Decimal Notation	Fraction Notation	Word Form
0.5	\(\ \frac{5}{10}\)	five tenths
0.34	\(\ \frac{34}{100}\)	thirty-four hundredths
0.896	\(\ \frac{896}{1,000}\)	eight hundred ninety-six thousandths

Notice that 0.5 has one decimal place. Its equivalent fraction, \(\ \frac{5}{10}\), has a denominator of 10—which is 1 followed by one zero. In general, when you are converting decimals to fractions, the denominator is always 1, followed by the number of zeros that correspond to the number of decimal places in the original number.

Another way to determine which number to place in the denominator is to use the place value of the last digit without the “ths” part. For example, if the number is 1.458, the 8 is in the thousandths place. Take away the “ths” and you have a thousand, so the number is written as \(\ 1 \frac{458}{1000}\).

Example

Write 0.68 in word form.

Solution

\(\ 0.68=\frac{68}{100}\)=sixty-eight hundredths

Note that the number is read as a fraction. Also note that the denominator has 2 zeros, the same as the number of decimal places in the original number.

The number 0.68 in word form is sixty-eight hundredths.

Recall that a mixed number is a combination of a whole number and a fraction. In the case of a decimal, a mixed number is also a combination of a whole number and a fraction, where the fraction is written as a decimal fraction.

To read mixed numbers, say the whole number part, the word “and” (representing the decimal point), and the number to the right of the decimal point, followed by the name and the place value of the last digit. You can see this demonstrated in the diagram below, in which the last digit is in the ten thousandths place.

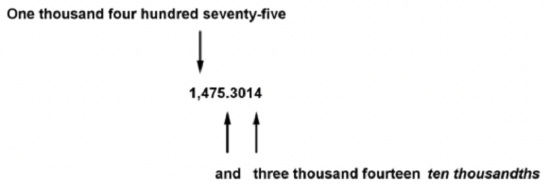
Another way to think about this is with money. Suppose you pay $ 15,264.25 for a car. You would read this as fifteen thousand, two hundred sixty-four dollars and twenty-five cents. In this case, the “cents” means “hundredths of a dollar,” so this is the same as saying fifteen thousand, two hundred sixty-four and twenty-five hundredths. A few more examples are shown in the table below.

Decimal Notation	Fraction Notation	Word Form
9.4	\(\ 9 \frac{4}{10}\)	Nine and four tenths
87.49	\(\ 87 \frac{49}{100}\)	Eighty-seven and forty-nine hundredths
594.236	\(\ 594 \frac{236}{1000}\)	Five hundred ninety-four and two hundred thirty-six thousandths

Example

Write 4.379 in word form.

Solution

\(\ 4.379=4 \frac{379}{1,000}\)= four and three hundred seventy-nine thousandths

The decimal fraction is read as a fraction. Note that the denominator has 3 zeros, the same as the number of decimal places in the original number.

The number 4.379 in word form is four and three hundred seventy-nine thousandths.

Exercise

Write 2.364 in word form.

1. two and three hundred sixty-four hundredths
2. two and three hundred sixty-four thousandths
3. two thousand three hundred sixty-four
4. three hundred sixty-four tenths and two

Answer

1. two and three hundred sixty-four hundredths

   Incorrect. You indicated the wrong decimal place in your answer. The correct answer is two and three hundred sixty-four thousandths.

2. Correct. 2.364 is the same as \(\ 2 \frac{364}{1,000}\), so in addition to the whole number 2, you have three hundred sixty-four thousandths.
3. Incorrect. You ignored the decimal point. The correct answer is a decimal; in this case, two and three hundred sixty-four thousandths.
4. Incorrect. You indicated the wrong decimal place in your answer, and the whole number part should be mentioned before the decimal part. The correct answer is two and three hundred sixty-four thousandths.

Writing Decimals as Simplified Fractions

As you have seen above, every decimal can be written as a fraction. To convert a decimal to a fraction, place the number after the decimal point in the numerator of the fraction and place the number 10,100, or 1,000, or another power of 10 in the denominator. For example, 0.5 would be written as \(\ \frac{5}{10}\). You’ll notice that this fraction can be further simplified, as \(\ \frac{5}{10}\) reduces to \(\ \frac{1}{2}\), which is the final answer.

Let’s get more familiar with this relationship between decimal places and zeros in the denominator by looking at several examples. Notice that in each example, the number of decimal places is different.

Example

Write 0.6 as a simplified fraction.

Solution

\(\ 0.6=\frac{6}{10}\)	The last decimal place is tenths, so use 10 for your denominator. The number of zeros in the denominator is always the same as the number of decimal places in the original decimal.
\(\ \frac{6 \div 2}{10 \div 2}=\frac{3}{5}\)	Simplify the fraction.

\(\ 0.6=\frac{3}{5}\)

Let’s look at an example in which a number with two decimal places is written as a fraction.

Example

Write 0.64 as a simplified fraction.

Solution

\(\ 0.64=\frac{64}{100}\)	The last decimal place is hundredths, so use 100 for your denominator. The number of zeros in the denominator is always the same as the number of decimal places in the original decimal.
\(\ \frac{64 \div 4}{100 \div 4}=\frac{16}{25}\)	Simplify the fraction.

\(\ 0.64=\frac{16}{25}\)

Now, examine how this is done in the example below using a decimal with digits in three decimal places.

Example

Write 0.645 as a simplified fraction.

Solution

\(\ 0.645=\frac{645}{1,000}\)	Note that there are 3 zeros in the denominator, which is the same as the number of decimal places in the original decimal.
\(\ \frac{645 \div 5}{1,000 \div 5}=\frac{129}{200}\)	Simplify the fraction.

\(\ 0.645=\frac{129}{200}\)

You can write a fraction as a decimal even when there are zeros to the right of the decimal point. Here is an example in which the only digit greater than zero is in the thousandths place.

Example

Write 0.007 as a simplified fraction.

Solution

\(\ 0.007=\frac{7}{1,000}\)

Note that 7 is in the thousandths place, so you write 1,000 in the denominator. The number of zeros in the denominator is always the same as the number of decimal places in the original decimal. The fraction cannot be simplified further.

\(\ 0.007=\frac{7}{1,000}\)

When writing decimals greater than 1, you only need to change the decimal part to a fraction and keep the whole number part. For example, 6.35 can be written as \(\ 6 \frac{35}{100}\).

Example

Write 8.65 as a simplified mixed fraction.

Solution

\(\ 8.65=8 \frac{65}{100}=8 \frac{13}{20}\)

Rewrite 0.65 as \(\ \frac{65}{100}\). Note that the number of zeros in the denominator is two, which is the same as the number of decimal places in the original decimal. Then simplify \(\ \frac{65}{100}\) by dividing numerator and denominator by 5.

\(\ 8.65=8 \frac{13}{20}\)

Exercise

Write 0.25 as a fraction.

1. \(\ \frac{2}{5}\)
2. \(\ \frac{1}{4}\)
3. \(\ \frac{4}{1}\)
4. \(\ \frac{5}{2}\)

Answer

1. Incorrect. You may have put the digit from the tenths place in the numerator, and the digit from the hundredths place in the denominator. The correct answer is \(\ \frac{1}{4}\).
2. Correct. The number 0.25 can be written as \(\ \frac{25}{100}\), which reduces to \(\ \frac{1}{4}\).
3. Incorrect. You probably confused the numerator and the denominator. The correct answer is \(\ \frac{1}{4}\).
4. Incorrect. You may have put the digit from the tenths place in the denominator, and the digit from the hundredths place in the numerator. The correct answer is \(\ \frac{1}{4}\).

Writing Fractions as Decimals

Just as you can write a decimal as a fraction, every fraction can be written as a decimal. To write a fraction as a decimal, divide the numerator (top) of the fraction by the denominator (bottom) of the fraction. Use long division, if necessary, and note where to place the decimal point in your answer. For example, to write \(\ \frac{3}{5}\) as a decimal, divide 3 by 5, which will result in 0.6.

Example

Write \(\ \frac{1}{2}\) as a decimal.

Solution

\(\ \begin{array}{r} 0.5 \ \\ 2 \longdiv {1.0} \\ -1.0 \ \\ \hline 0\ \end{array}\)

Using long division, you can see that dividing 1 by 2 results in 0.5.

\(\ \frac{1}{2}=0.5\)

Note that you could also have thought about the problem like this: \(\ \frac{1}{2}=\frac{?}{10}\), and then solved for?. One way to think about this problem is that 10 is five times greater than 2, so will have to be five times greater than 1. What number is five times greater than 1? Five is, so the solution is \(\ \frac{1}{2}=\frac{5}{10}\).

Now look at a more complex example, where the final digit of the answer is in the thousandths place.

Example

Write \(\ \frac{3}{8}\) as a decimal.

Solution

\(\ \begin{array}{r} 0.375\ \\ 8 \longdiv {3.000} \\ -24 \ \ \ \ \ \ \\ \hline 60 \ \ \ \ \\ -56 \ \ \ \ \\ \hline 40\ \ \\ -40 \ \ \\ \hline 0\ \ \end{array}\)

Using long division, you can see that dividing 3 by 8 results in 0.375.

\(\ \frac{3}{8}=0.375\)

Converting from fractions to decimals sometimes results in answers with decimal numbers that begin to repeat. For example, \(\ \frac{2}{3}\) converts to 0.666, a repeating decimal, in which the 6 repeats infinitely. You would write this as \(\ 0 . \overline{6}\), with a bar over the first decimal digit to indicate that the 6 repeats. Look at this example of a problem in which two consecutive digits in the answer repeat.

Example

Convert \(\ \frac{4}{11}\) to a decimal.

Solution

\(\ \begin{array}{r} 0.3636 \ \\ 11\longdiv {4.0000} \\ -33\ \ \ \ \ \ \ \\ \hline 70 \ \ \ \ \ \\ -66 \ \ \ \ \ \\ \hline 40 \ \ \ \\ -33 \ \ \ \\ \hline 70\ \\ -66 \ \\ \hline 4\ \end{array}\)

Using long division, you can see that dividing 4 by 11 results in 0.36 repeating. As a result, this is written with a line over it as \(\ 0 . \overline{36}\).

\(\ \frac{4}{11}=0 . \overline{36}\)

With numbers greater than 1, keep the whole number part of the mixed number as the whole number in the decimal. Then use long division to convert the fraction part to a decimal. For example, \(\ 2 \frac{3}{20}\) can be written as 2.15.

Example

Convert \(\ 2 \frac{1}{4}\) to a decimal.

Solution

\(\ \begin{array}{r} 0.25 \ \\ 4\longdiv{1.00} \\ -8 \ \ \ \\ \hline 20 \ \\ -20 \ \\ \hline 0\ \end{array}\)	Knowing that the whole number 2 will remain the same during the conversion, focus only on the decimal part. Using long division, you can see that dividing 1 by 4 results in 0.25.
\(\ 2+0.25=2.25\)	Now bring back the whole number 2, and the resulting fraction is 2.25.

\(\ 2 \frac{1}{4}=2.25\)

Tips on Converting Fractions to Decimals

To write a fraction as a decimal, divide the numerator (top) of the fraction by the denominator (bottom) of the fraction.

In the case of repeating decimals, write the repeating digit or digits with a line over it. For example, 0.333 repeating would be written as \(\ 0 . \overline{3}\).

Summary

Decimal notation is another way to write numbers that are less than 1 or that combine whole numbers with decimal fractions, sometimes called mixed numbers. When you write numbers in decimal notation, you can use an extended place-value chart that includes positions for numbers less than one. You can write numbers written in fraction notation (fractions) in decimal notation (decimals), and you can write decimals as fractions. You can always convert between fractional notation and decimal notation.