Chapter 11 Review Exercises
- Last updated
- Jun 14, 2019
- Save as PDF
- Page ID
- 20997
( \newcommand{\kernel}{\mathrm{null}\,}\)
For exercises 1 - 4, determine whether the statement is true or false. Justify the answer with a proof or a counterexample.
1) For vectors
- Answer
- True; See proof in Section 11.3
2) For vectors
3) The symmetric equation for the line of intersection between two planes
- Answer
- False, Converting the symmetric equations above to the parametric equations of the line, we get:
If this line lies on each plane, we should get an identity (like 5 = 5) when we substitute each expression ofin the each plane's equation.
Substituting into the first plane equation, we get:
Thus we know that this line does lie on the first plane.
But when we substitute into the second plane equation, we obtain:
Since we do not get an identity, we know this line is not on the second plane and can therefore not be the line of intersection of the two planes.
4) If
- Answer
- False, since
or could also be the zero vector.
For exercises 5 and 6, use the given vectors to find the quantities.
5)
a.
b.
c.
d.
- Answer
- a.
b.
c. Can’t cross a vector with a scalar
d.
6)
a.
b.
c.
d.
e.
7) Find the values of
- Answer
For exercises 8 and 9, find the unit vectors.
8) Find the unit vector that has the same direction as vector
9) Find the unit vector that has the same direction as vector
- Answer
For exercises 10 and 11, find the area or volume of the given shapes.
10) The parallelogram spanned by vectors
11) The parallelepiped formed by
- Answer
units
For exercises 12 and 13, find the parametric equations and the vector equation of the line with the given properties.
12) The line that passes through point
13) The line that passes through points
- Answer
For exercises 14 and 15, find the equation of the plane with the given properties.
14) The plane that passes through point
15) The plane that passes through points
- Answer
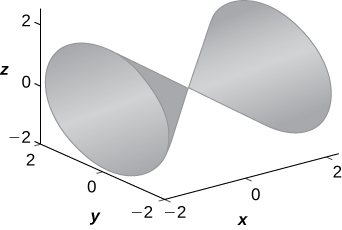
For exercises 16 and 17, find the traces for the surfaces in planes
16)
17)
- Answer
For exercises 18 and 19, write the given equation in cylindrical coordinates and spherical coordinates.
18)
19)
- Answer
- Cylindrical:
For exercises 20 and 21, convert the given equations from cylindrical or spherical coordinates to rectangular coordinates. Identify the given surface.
20)
21)
- Answer
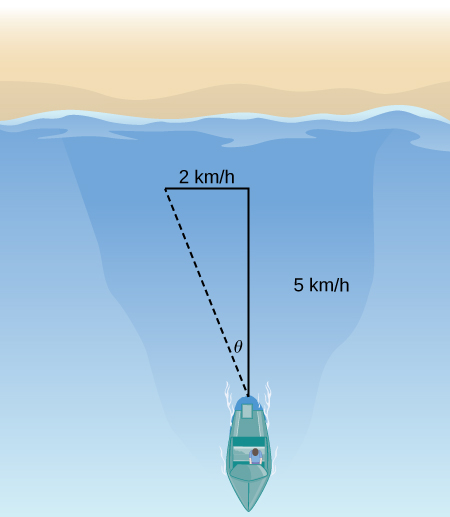
For exercises 22 and 23, consider a small boat crossing a river.
22) If the boat velocity is
23) When the boat reaches the shore, two ropes are thrown to people to help pull the boat ashore. One rope is at an angle of
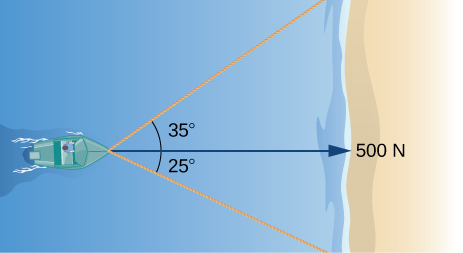
- Answer
- 331 N and 244 N
24) An airplane is flying in the direction of 52° east of north with a speed of 450 mph. A strong wind has a bearing 33° east of north with a speed of 50 mph. What is the resultant ground speed and bearing of the airplane?
25) Calculate the work done by moving a particle from position
- Answer
J
In problems 26 and 27, consider your unsuccessful attempt to take the tire off your car using a wrench to loosen the bolts. Assume the wrench is 0.3 m long and you are able to apply a 200-N force.
26) Because your tire is flat, you are only able to apply your force at a
27) Someone lends you a tire jack and you are now able to apply a 200-N force at an
- Answer
- More,
J
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

