Arc Length and Curvature
- Last updated
- Jun 14, 2019
- Save as PDF
- Page ID
- 21006
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we study formulas related to curves in both two and three dimensions, and see how they are related to various properties of the same curve. For example, suppose a vector-valued function describes the motion of a particle in space. We would like to determine how far the particle has traveled over a given time interval, which can be described by the arc length of the path it follows. Or, suppose that the vector-valued function describes a road we are building and we want to determine how sharply the road curves at a given point. This is described by the curvature of the function at that point. We explore each of these concepts in this section.
Arc Length for Vector Functions
We have seen how a vector-valued function describes a curve in either two or three dimensions. Recall that the formula for the arc length of a curve defined by the parametric functions
In a similar fashion, if we define a smooth curve using a vector-valued function
In three dimensions, if the vector-valued function is described by
Theorem: Arc-Length Formulas for Plane and Space curves
Plane curve: Given a smooth curve
Space curve: Given a smooth curve
The two formulas are very similar; they differ only in the fact that a space curve has three component functions instead of two. Note that the formulas are defined for smooth curves: curves where the vector-valued function
We now return to the helix introduced earlier in this chapter. A vector-valued function that describes a helix can be written in the form
where
Therefore,
This gives a formula for the length of a wire needed to form a helix with
Arc-Length Parameterization
We now have a formula for the arc length of a curve defined by a vector-valued function. Let’s take this one step further and examine what an arc-length function is.
If a vector-valued function represents the position of a particle in space as a function of time, then the arc-length function measures how far that particle travels as a function of time. The formula for the arc-length function follows directly from the formula for arc length:
If the curve is in two dimensions, then only two terms appear under the square root inside the integral. The reason for using the independent variable u is to distinguish between time and the variable of integration. Since
If we assume that
which means that
Theorem: Arc-Length Function
Let
Furthermore,
A useful application of this theorem is to find an alternative parameterization of a given curve, called an arc-length parameterization. Recall that any vector-valued function can be reparameterized via a change of variables. For example, if we have a function
Suppose that we find the arc-length function
Example
Find the arc-length parameterization for each of the following curves:
Solution
- First we find the arc-length function using Equation
which gives the relationship between the arc length
This is the arc-length parameterization of - The arc-length function is given by Equation
Therefore, the relationship between the arc length
This is an arc-length parameterization of
Exercise
Find the arc-length function for the helix
Then, use the relationship between the arc length and the parameter
- Hint
-
Start by finding the arc-length function.
- Answer
-
Curvature
An important topic related to arc length is curvature. The concept of curvature provides a way to measure how sharply a smooth curve turns. A circle has constant curvature. The smaller the radius of the circle, the greater the curvature.
Think of driving down a road. Suppose the road lies on an arc of a large circle. In this case you would barely have to turn the wheel to stay on the road. Now suppose the radius is smaller. In this case you would need to turn more sharply to stay on the road. In the case of a curve other than a circle, it is often useful first to inscribe a circle to the curve at a given point so that it is tangent to the curve at that point and “hugs” the curve as closely as possible in a neighborhood of the point (Figure
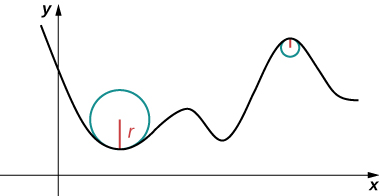
Definition: curvature
Let
As the unit vector
The formula in the definition of curvature is not very useful in terms of calculation. In particular, recall that
To use the formula for curvature, it is first necessary to express
Theorem: Alternate Formulas of Curvature
If
If
Note that in the context of motion, this formula could also be written
If
Proof
The first formula follows directly from the chain rule:
where
Since
In the case of a three-dimensional curve, we start with the formulas
Using these last two equations we get
Since
Since
Now we solve this equation for
Then, we divide both sides by
This proves
Therefore,
Note that in the context of motion, the first alternate formula can be rewritten
Considering what was stated above about the curvature being a measure of the speed at which the direction of motion is changing at a point, notice that we have normalized this measurement this time by dividing out the actual speed of travel along the curve at the given instant.
As indicated above, the second alternate formula can be rewritten as
Remember that the cross product measures the extent to which the two vectors are aligned, returning its largest value when they are orthogonal. Note also that the component of acceleration that is orthogonal to the velocity is the only part we care about here, as it is the component that will affect the change of direction of the motion. The component of acceleration that is aligned with the velocity (and tangent to the curve) will only affect the speed of the motion, which is being ignored in our measurement of curvature. Note that one factor of
Example
Find the curvature for each of the following curves at the given point:
Solution
- This function describes a helix.
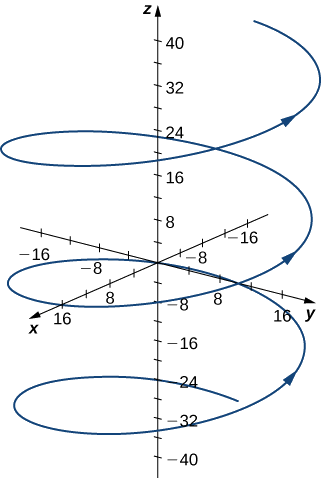
The curvature of the helix at
Next, calculate
The curvature of this helix is constant at all points on the helix.
- This function describes a semicircle.
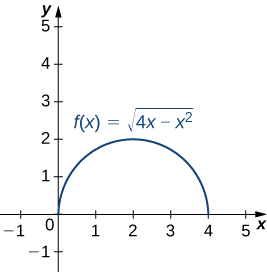
To find the curvature of this graph, we must use
The curvature of this circle is equal to the reciprocal of its radius. There is a minor issue with the absolute value in
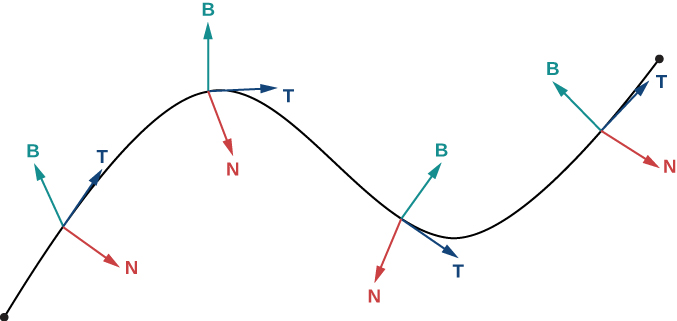
The Normal and Binormal Vectors
We have seen that the derivative
Definition: binormal vectors
Let
The binormal vector at
where
Note that, by definition, the binormal vector is orthogonal to both the unit tangent vector and the normal vector. Furthermore,
where
The principal unit normal vector can be challenging to calculate because the unit tangent vector involves a quotient, and this quotient often has a square root in the denominator. In the three-dimensional case, finding the cross product of the unit tangent vector and the unit normal vector can be even more cumbersome. Fortunately, we have alternative formulas for finding these two vectors, and they are presented in Motion in Space.
Example
For each of the following vector-valued functions, find the principal unit normal vector. Then, if possible, find the binormal vector.
Solution
- This function describes a circle.
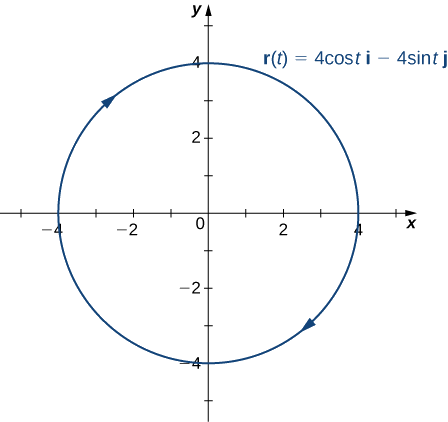
To find the principal unit normal vector, we first must find the unit tangent vector
Notice that the unit tangent vector and the principal unit normal vector are orthogonal to each other for all values of
Furthermore, the principal unit normal vector points toward the center of the circle from every point on the circle. Since
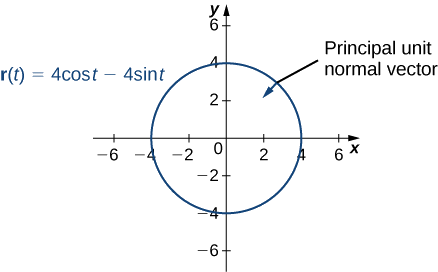
- This function looks like this:
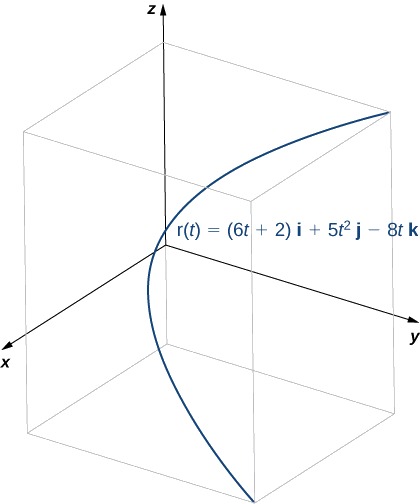
To find the principal unit normal vector, we first find the unit tangent vector
Next, we calculate
Once again, the unit tangent vector and the principal unit normal vector are orthogonal to each other for all values of
Last, since
For any smooth curve in three dimensions that is defined by a vector-valued function, we now have formulas for the unit tangent vector
Suppose we form a circle in the osculating plane of
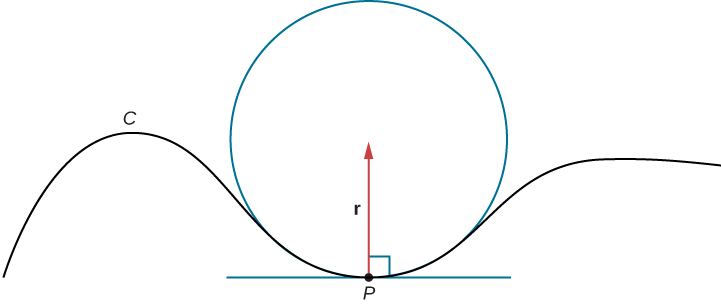
For more information on osculating circles, see this demonstration on curvature and torsion, this article on osculating circles, and this discussion of Serret formulas.
To find the equation of an osculating circle in two dimensions, we need find only the center and radius of the circle.
Example
Find the equation of the osculating circle of the curve defined by the function
Solution
Figure

First, let’s calculate the curvature at
This gives
Exercise
Find the equation of the osculating circle of the curve defined by the vector-valued function
- Hint
-
Use
- Answer
-
At the point
A graph of this function appears next:
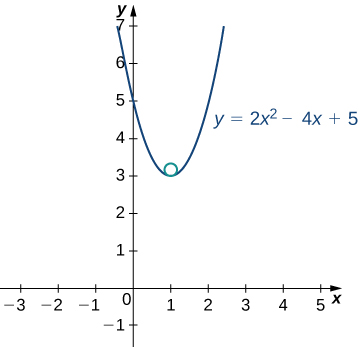
The vertex of this parabola is located at the point
Key Concepts
- The arc-length function for a vector-valued function is calculated using the integral formula
- The curvature of a curve at a point in either two or three dimensions is defined to be the curvature of the inscribed circle at that point. The arc-length parameterization is used in the definition of curvature.
- There are several different formulas for curvature. The curvature of a circle is equal to the reciprocal of its radius.
- The principal unit normal vector at
- The binormal vector at
- The Frenet frame of reference is formed by the unit tangent vector, the principal unit normal vector, and the binormal vector.
- The osculating circle is tangent to a curve at a point and has the same curvature as the tangent curve at that point.
Key Equations
- Arc length of space curve
- Arc-length function
- Curvature
- Principal unit normal vector
- Binormal vector
- arc-length function
- a function
- arc-length parameterization
- a reparameterization of a vector-valued function in which the parameter is equal to the arc length
- binormal vector
- a unit vector orthogonal to the unit tangent vector and the unit normal vector
- curvature
- the derivative of the unit tangent vector with respect to the arc-length parameter
- Frenet frame of reference
- (TNB frame) a frame of reference in three-dimensional space formed by the unit tangent vector, the unit normal vector, and the binormal vector
- normal plane
- a plane that is perpendicular to a curve at any point on the curve
- osculating circle
- a circle that is tangent to a curve
- osculating plane
- the plane determined by the unit tangent and the unit normal vector
- principal unit normal vector
- a vector orthogonal to the unit tangent vector, given by the formula
- radius of curvature
- the reciprocal of the curvature
- smooth
- curves where the vector-valued function
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


