Exercises for Section 12.4

Determining Arc Length

In questions 1 - 5, find the arc length of the curve on the given interval.

1) \(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+(2t^2+1)\,\hat{\mathbf{j}}, \quad 1≤t≤3\). This portion of the graph is shown here:

Answer

\(8\sqrt{5}\) units \( \approx 17.9\) units

2) \(\vecs r(t)=t^2 \,\hat{\mathbf{i}}+14t \,\hat{\mathbf{j}},\quad 0≤t≤7\). This portion of the graph is shown here:

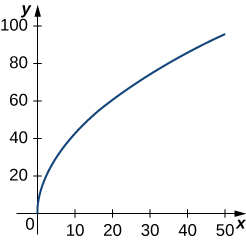
3) \(\vecs r(t)=⟨t^2+1,4t^3+3⟩, \quad −1≤t≤0\). This portion of the graph is shown here:

Answer

\(\frac{1}{54}(37^{3/2}−1)\) units \( \approx 4.15\) units

4) \(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩,\quad 0≤t≤π\). This portion of the graph is shown here:

5) \(\vecs r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩\) over the interval \([0,\frac{π}{2}]\). Here is the portion of the graph on the indicated interval:

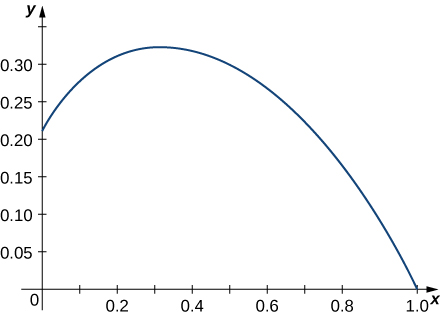
6) Set up an integral to represent the arc length from \(t = 0\) to \(t = 2\) along the curve traced out by \(\vecs r(t) = \langle t, \, t^4\rangle.\) Then use technology to approximate this length to the nearest thousandth of a unit.

7) Find the length of one turn of the helix given by \(\vecs r(t)= \frac{1}{2} \cos t \,\hat{\mathbf{i}}+\frac{1}{2} \sin t \,\hat{\mathbf{j}}+\frac{\sqrt{3}}{2}\,t \,\hat{\mathbf{k}}\).

Answer

Length \(=2π\) units

8) Find the arc length of the vector-valued function \(\vecs r(t)=−t \,\hat{\mathbf{i}}+4t \,\hat{\mathbf{j}}+3t \,\hat{\mathbf{k}}\) over \([0,1]\).

9) A particle travels in a circle with the equation of motion \(\vecs r(t)=3 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}} +0 \,\hat{\mathbf{k}}\). Find the distance traveled around the circle by the particle.

Answer

\(6π\) units

10) Set up an integral to find the circumference of the ellipse with the equation \(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+2 \sin t \,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}\).

11) Find the length of the curve \(\vecs r(t)=⟨\sqrt{2}t,\, e^t, \, e^{−t}⟩\) over the interval \(0≤t≤1\). The graph is shown here:

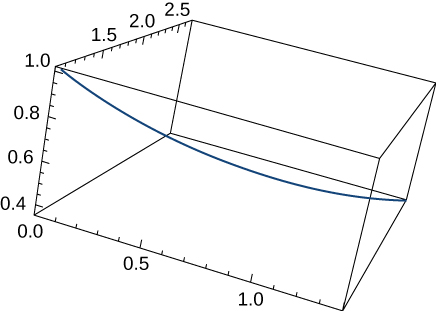
Answer

\(\left(e−\frac{1}{e}\right)\) units \( \approx 2.35\) units

12) Find the length of the curve \(\vecs r(t)=⟨2 \sin t, \, 5t, \, 2 \cos t⟩\) for \(t∈[−10,10]\).

Unit Tangent Vectors and Unit Normal Vectors

13) The position function for a particle is \(\vecs r(t)=a \cos( ωt) \,\hat{\mathbf{i}}+b \sin (ωt) \,\hat{\mathbf{j}}\). Find the unit tangent vector and the unit normal vector at \(t=0\).

Solution:

\(\begin{align*} \vecs r'(t) &= -aω \sin( ωt) \,\hat{\mathbf{i}}+bω \cos (ωt) \,\hat{\mathbf{j}}\\[5pt]
\| \vecs r'(t) \| &= \sqrt{a^2 ω^2 \sin^2(ωt) +b^2ω^2\cos^2(ωt)} \\[5pt]
\vecs T(t) &= \dfrac{\vecs r'(t)}{\| \vecs r'(t) \| } = \dfrac{-aω \sin( ωt) \,\hat{\mathbf{i}}+bω \cos (ωt) \,\hat{\mathbf{j}}}{\sqrt{a^2 ω^2 \sin^2(ωt) +b^2ω^2\cos^2(ωt)}}\\[5pt]
\vecs T(0) &= \dfrac{bω \,\hat{\mathbf{j}}}{\sqrt{(bω)^2}} = \dfrac{bω \,\hat{\mathbf{j}}}{|bω|}\end{align*}\)

If \(bω > 0, \; \vecs T(0) = \hat{\mathbf{j}},\) and if \( bω < 0, \; T(0)= -\hat{\mathbf{j}}\)

Answer

If \(bω > 0, \; \vecs T(0)= \hat{\mathbf{j}},\) and if \( bω < 0, \; \vecs T(0)= -\hat{\mathbf{j}}\)

If \(a > 0, \; \vecs N(0)= -\hat{\mathbf{i}},\) and if \( a < 0, \; \vecs N(0)= \hat{\mathbf{i}}\)

14) Given \(\vecs r(t)=a \cos (ωt) \,\hat{\mathbf{i}} +b \sin (ωt) \,\hat{\mathbf{j}}\), find the binormal vector \(\vecs B(0)\).

15) Given \(\vecs r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩\), determine the unit tangent vector \(\vecs T(t)\).

Answer

\(\begin{align*} \vecs T(t) &=\left\langle \frac{2}{\sqrt{6}},\, \frac{\cos t− \sin t}{\sqrt{6}}, \, \frac{\cos t+ \sin t}{\sqrt{6}}\right\rangle \\[4pt]
&= \left\langle\frac{\sqrt{6}}{3},\, \frac{\sqrt{6}}{6} (\cos t− \sin t), \, \frac{\sqrt{6}}{6} (\cos t+ \sin t)\right\rangle \end{align*}\)

16) Given \(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), find the unit tangent vector \(\vecs T(t)\) evaluated at \(t=0\), \(\vecs T(0)\).

17) Given \(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), determine the unit normal vector \(\vecs N(t)\).

Answer

\(\vecs N(t)=⟨0,\, -\frac{\sqrt{2}}{2} (\sin t + \cos t), \, \frac{\sqrt{2}}{2} (\cos t- \sin t)⟩\)

18) Given \(\vecs r(t)=⟨2e^t,\, e^t \cos t,\, e^t \sin t⟩\), find the unit normal vector \(\vecs N(t)\) evaluated at \(t=0\), \(\vecs N(0)\).

Answer

\(\vecs N(0)=⟨0, \;-\frac{\sqrt{2}}{2},\;\frac{\sqrt{2}}{2}⟩\)

19) Given \(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\), find the unit tangent vector \(\vecs T(t)\). The graph is shown here:

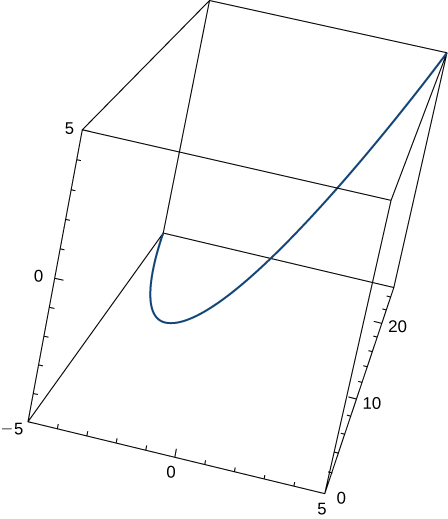
Answer

\(\vecs T(t)=\dfrac{1}{\sqrt{4t^2+2}}<1,2t,1>\)

20) Find the unit tangent vector \(\vecs T(t)\) and unit normal vector \(\vecs N(t)\) at \(t=0\) for the plane curve \(\vecs r(t)=⟨t^3−4t,5t^2−2⟩\). The graph is shown here:

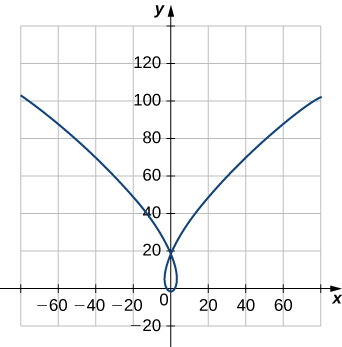
21) Find the unit tangent vector \(\vecs T(t)\) for \(\vecs r(t)=3t \,\hat{\mathbf{i}}+5t^2 \,\hat{\mathbf{j}}+2t \,\hat{\mathbf{k}}\).

Answer

\(\vecs T(t)=\dfrac{1}{\sqrt{100t^2+13}}(3 \,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}+2 \,\hat{\mathbf{k}})\)

22) Find the principal normal vector to the curve \(\vecs r(t)=⟨6 \cos t,6 \sin t⟩\) at the point determined by \(t=\frac{π}{3}\).

23) Find \(\vecs T(t)\) for the curve \(\vecs r(t)=(t^3−4t) \,\hat{\mathbf{i}}+(5t^2−2) \,\hat{\mathbf{j}}\).

Answer

\(\vecs T(t)=\dfrac{1}{\sqrt{9t^4+76t^2+16}}\big((3t^2−4)\,\hat{\mathbf{i}}+10t \,\hat{\mathbf{j}}\big)\)

24) Find \(\vecs N(t)\) for the curve \(\vecs r(t)=(t^3−4t)\,\hat{\mathbf{i}}+(5t^2−2)\,\hat{\mathbf{j}}\).

25) Find the unit tangent vector \(\vecs T(t)\) for \(\vecs r(t)=⟨2 \sin t,\, 5t,\, 2 \cos t⟩\).

Answer

\(\vecs T(t)=⟨\frac{2\sqrt{29}}{29}\cos t,\, \frac{5\sqrt{29}}{29},\,−\frac{2\sqrt{29}}{29}\sin t⟩\)

26) Find the unit normal vector \(\vecs N(t)\) for \(\vecs r(t)=⟨2\sin t,\,5t,\,2\cos t⟩\).

Answer

\(\vecs N(t)=⟨−\sin t,\, 0,\, −\cos t⟩\)

Arc Length Parameterizations

27) Find the arc-length function \(\vecs s(t)\) for the line segment given by \(\vecs r(t)=⟨3−3t,\, 4t⟩\). Then write the arc-length parameterization of \(r\) with \(s\) as the parameter.

Answer

Arc-length function: \(s(t)=5t\); The arc-length parameterization of \(\vecs r(t)\): \(\vecs r(s)=\left(3−\dfrac{3s}{5}\right)\,\hat{\mathbf{i}}+\dfrac{4s}{5}\,\hat{\mathbf{j}}\)

28) Parameterize the helix \(\vecs r(t)= \cos t \,\hat{\mathbf{i}}+ \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) using the arc-length parameter \(s\), from \(t=0\).

29) Parameterize the curve using the arc-length parameter \(s\), at the point at which \(t=0\) for \(\vecs r(t)=e^t \sin t \,\hat{\mathbf{i}} + e^t \cos t \,\hat{\mathbf{j}}\)

Answer

\(\vecs r(s)=\left(1+\dfrac{s}{\sqrt{2}}\right) \sin \left( \ln \left(1+ \dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{i}} +\left(1+ \dfrac{s}{\sqrt{2}}\right) \cos \left( \ln \left(1+\dfrac{s}{\sqrt{2}}\right)\right)\,\hat{\mathbf{j}}\)

Curvature and the Osculating Circle

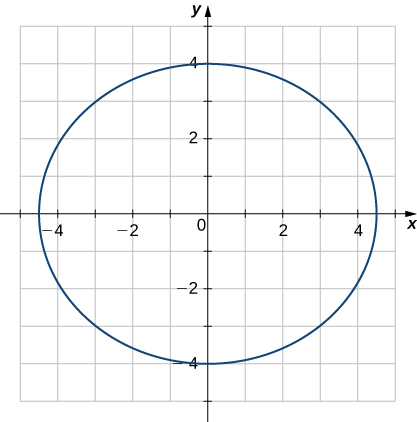
30) Find the curvature of the curve \(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}\) at \(t=π/3\). (Note: The graph is an ellipse.)

31) Find the \(x\)-coordinate at which the curvature of the curve \(y=1/x\) is a maximum value.

Answer

The maximum value of the curvature occurs at \(x=1\).

32) Find the curvature of the curve \(\vecs r(t)=5 \cos t \,\hat{\mathbf{i}}+5 \sin t \,\hat{\mathbf{j}}\). Does the curvature depend upon the parameter \(t\)?

33) Find the curvature \(κ\) for the curve \(y=x−\frac{1}{4}x^2\) at the point \(x=2\).

Answer

\(\frac{1}{2}\)

34) Find the curvature \(κ\) for the curve \(y=\frac{1}{3}x^3\) at the point \(x=1\).

35) Find the curvature \(κ\) of the curve \(\vecs r(t)=t \,\hat{\mathbf{i}}+6t^2 \,\hat{\mathbf{j}}+4t \,\hat{\mathbf{k}}\). The graph is shown here:

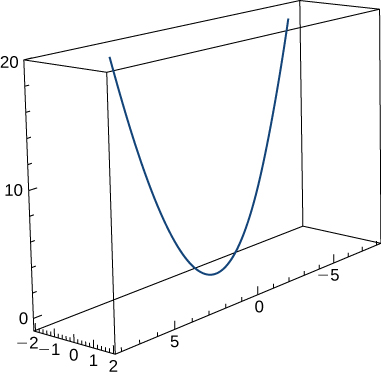
Answer

\(κ≈\dfrac{49.477}{(17+144t^2)^{3/2}}\)

36) Find the curvature of \(\vecs r(t)=⟨2 \sin t,5t,2 \cos t⟩\).

37) Find the curvature of \(\vecs r(t)=\sqrt{2}t \,\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}+e^{−t} \,\hat{\mathbf{k}}\) at point \(P(0,1,1)\).

Answer

\(\frac{1}{2\sqrt{2}}\)

38) At what point does the curve \(y=e^x\) have maximum curvature?

39) What happens to the curvature as \(x→∞\) for the curve \(y=e^x\)?

Answer

The curvature approaches zero.

40) Find the point of maximum curvature on the curve \(y=\ln x\).

41) Find the equations of the normal plane and the osculating plane of the curve \(\vecs r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩\) at point \((0,π,−2)\).

Answer

\(y=6x+π\) and \(x+6y=6π\)

42) Find equations of the osculating circles of the ellipse \(4y^2+9x^2=36\) at the points \((2,0)\) and \((0,3)\).

43) Find the equation for the osculating plane at point \(t=π/4\) on the curve \(\vecs r(t)=\cos (2t) \,\hat{\mathbf{i}}+ \sin (2t) \,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}\).

Answer

\(x+2z=\frac{π}{2}\)

44) Find the radius of curvature of \(6y=x^3\) at the point \((2,\frac{4}{3}).\)

45) Find the curvature at each point \((x,y)\) on the hyperbola \(\vecs r(t)=⟨a \cosh( t),b \sinh (t)⟩\).

Answer

\(\dfrac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}\)

46) Calculate the curvature of the circular helix \(\vecs r(t)=r \sin (t) \,\hat{\mathbf{i}}+r \cos (t) \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\).

47) Find the radius of curvature of \(y= \ln (x+1)\) at point \((2,\ln 3)\).

Answer

\(\frac{10\sqrt{10}}{3}\)

48) Find the radius of curvature of the hyperbola \(xy=1\) at point \((1,1)\).

A particle moves along the plane curve \(C\) described by \(\vecs r(t)=t \,\hat{\mathbf{i}}+t^2 \,\hat{\mathbf{j}}\). Use this parameterization to answer questions 49 - 51.

49) Find the length of the curve over the interval \([0,2]\).

Answer

\(\frac{1}{4}\big[ 4\sqrt{17} + \ln\left(4+\sqrt{17}\right)\big]\text{ units }\approx 4.64678 \text{ units}\)

50) Find the curvature of the plane curve at \(t=0,1,2\).

51) Describe the curvature as t increases from \(t=0\) to \(t=2\).

Answer

The curvature is decreasing over this interval.

The surface of a large cup is formed by revolving the graph of the function \(y=0.25x^{1.6}\) from \(x=0\) to \(x=5\) about the \(y\)-axis (measured in centimeters).

52) [T] Use technology to graph the surface.

53) Find the curvature \(κ\) of the generating curve as a function of \(x\).

Answer

\(κ=\dfrac{30}{x^{2/5}\left(25+4x^{6/5}\right)^{3/2}}\)

Note that initially your answer may be:
\(\dfrac{6}{25x^{2/5}\left(1+\frac{4}{25}x^{6/5}\right)^{3/2}}\)

We can simplify it as follows:
\( \begin{align*} \dfrac{6}{25x^{2/5}\left(1+\frac{4}{25}x^{6/5}\right)^{3/2}} &= \dfrac{6}{25x^{2/5}\big[\frac{1}{25}\left(25+4x^{6/5}\right)\big]^{3/2}}\\[4pt]
&= \dfrac{6}{25x^{2/5}\left(\frac{1}{25}\right)^{3/2}\big[25+4x^{6/5}\big]^{3/2}} \\[4pt]
&= \dfrac{6}{\frac{25}{125}x^{2/5}\big[25+4x^{6/5}\big]^{3/2}} \\[4pt]
&= \dfrac{30}{x^{2/5}\left(25+4x^{6/5}\right)^{3/2}}\end{align*} \)

54) [T] Use technology to graph the curvature function.

Contributors:

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

• Paul Seeburger (Monroe Community College) created question 6.