Skip to main content
Mathematics LibreTexts

Tangent Planes, Linear Approximations, and the Total Differential (Exercises)

  1. Last updated
  2. Save as PDF
  • Page ID
    21020

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    In exercises 1 - 2, find a unit normal vector to the surface at the indicated point.

    1) \( f(x,y)=x^3,\quad (2,−1,8)\)

    Answer
    \( (\frac{\sqrt{145}}{145})(12\hat{\mathbf i}−\hat{\mathbf k})\)

    2) \( \ln\left(\dfrac{x}{y−z}\right)=0\) when \( x=y=1\)

    In exercises 3 - 7, find a normal vector and a tangent vector at point \( P\).

    3) \( x^2+xy+y^2=3,\quad P(−1,−1)\)

    Answer
    Normal vector: \( \hat{\mathbf i}+\hat{\mathbf j}\), tangent vector: \( \hat{\mathbf i}−\hat{\mathbf j}\)

    4) \( (x^2+y^2)^2=9(x^2−y^2),\quad P(\sqrt{2},1)\)

    5) \( xy^2−2x^2+y+5x=6,\quad P(4,2)\)

    Answer
    Normal vector: \( 7\hat{\mathbf i}−17\hat{\mathbf j}\), tangent vector: \( 17\hat{\mathbf i}+7\hat{\mathbf j}\)

    6) \( 2x^3−x^2y^2=3x−y−7,\quad P(1,−2)\)

    7) \( ze^{x^2−y^2}−3=0, \quad P(2,2,3)\)

    Answer
    Normal vector: \( -12\hat{\mathbf i}+12\hat{\mathbf j}-\hat{\mathbf k}\) or \( 12\hat{\mathbf i}-12\hat{\mathbf j}+\hat{\mathbf k}\),
    Tangent vector: \( 0\hat{\mathbf i}+1\hat{\mathbf j}+12\hat{\mathbf k}\) or \( 1\hat{\mathbf i}+0\hat{\mathbf j}-12\hat{\mathbf k}\)

    In exercises 8 - 19, find the equation for the tangent plane to the surface at the indicated point. (Hint: If the given function is not already solved for \(z\), start by solving it for \( z\) in terms of \( x\) and \( y\).)

    8) \( −8x−3y−7z=−19,\quad P(1,−1,2)\)

    9) \( z=−9x^2−3y^2,\quad P(2,1,−39)\)

    Answer
    \( −36x−6y−z=−39\)

    10) \( x^2+10xyz+y^2+8z^2=0,\quad P(−1,−1,−1)\)

    11) \( z=\ln(10x^2+2y^2+1),\quad P(0,0,0)\)

    Answer
    \( z=0\)

    12) \( z=e^{7x^2+4y^2}, \quad P(0,0,1)\)

    13) \( xy+yz+zx=11,\quad P(1,2,3)\)

    Answer
    \( 5x+4y+3z−22=0\)

    14) \( x^2+4y^2=z^2,\quad P(3,2,5)\)

    15) \( x^3+y^3=3xyz,\quad P(1,2,\frac{3}{2})\)

    Answer
    \( 4x−5y+4z=0\)

    16) \( z=axy,\quad P(1,\frac{1}{a},1)\)

    17) \( z=\sin x+\sin y+\sin(x+y),\quad P(0,0,0)\)

    Answer
    \( 2x+2y−z=0\)

    18) \( h(x,y)=\ln\sqrt{x^2+y^2},\quad P(3,4)\)

    19) \( z=x^2−2xy+y^2,\quad P(1,2,1)\)

    Answer
    \( −2(x−1)+2(y−2)−(z−1)=0\)

    In exercises 20 - 25, find parametric equations for the normal line to the surface at the indicated point. (Recall that to find the equation of a line in space, you need a point on the line, \( P_0(x_0,y_0,z_0)\), and a vector \( \vecs v=⟨a,b,c⟩\) that is parallel to the line. Then the equations of the line are: \(\quad x=x_0+at,\quad y=y_0+bt, \quad z=z_0+ct.)\)

    20) \( −3x+9y+4z=−4,\quad P(1,−1,2)\)

    21) \( z=5x^2−2y^2,\quad P(2,1,18)\)

    Answer
    \( x=20t+2,y=−4t+1,z=−t+18\)

    22) \( x^2−8xyz+y^2+6z^2=0,\quad P(1,1,1)\)

    23) \( z=\ln(3x^2+7y^2+1),\quad P(0,0,0)\)

    Answer
    \( x=0,y=0,z=t\)

    24) \( z=e^{4x^2+6y^2},\quad P(0,0,1)\)

    25) \( z=x^2−2xy+y^2\) at point \( P(1,2,1)\)

    Answer
    \( x−1=2t;y−2=−2t;z−1=t\)

    In exercises 26 - 28, use the figure shown here.

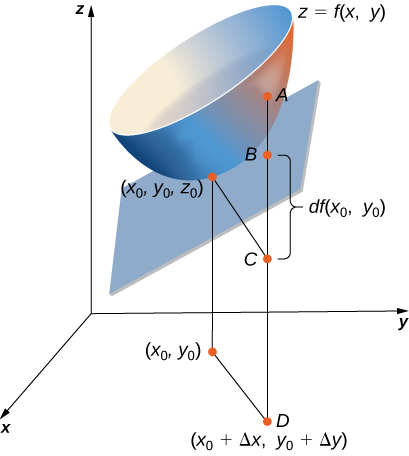
    Diagram showing differential of f at the point (x_0, y_0)

    26) The length of line segment \( AC\) is equal to what mathematical expression?

    27) The length of line segment \( BC\) is equal to what mathematical expression?

    Answer
    The differential of the function \( z(x,y)=dz=f_xdx+f_ydy\)

    28) Using the figure, explain what the length of line segment \( AB\) represents.

    29) Show that \( f(x,y)=e^{xy}x\) is differentiable at point \( (1,0).\)

    Answer
    Using the definition of differentiability, we have \( e^{xy}x≈x+y\).

    30) Show that \( f(x,y)=x^2+3y\) is differentiable at every point. In other words, show that \( Δz=f(x+Δx,y+Δy)−f(x,y)=f_xΔx+f_yΔy+ε_1Δx+ε_2Δy\), where both \( ε_1\) and \( ε_2\) approach zero as \( (Δx,Δy)\) approaches \( (0,0).\)

    Answer
    \( Δz=2xΔx+3Δy+(Δx)^2.(Δx)^2→0\) for small \( Δx\) and \( z\) satisfies the definition of differentiability.

    31) Find the total differential of each function:

    1. \( z=x^3 + y^3 - 5\)
    2. \( z=e^{xy}\)
    3. \( z=y\cos x+\sin y\)
    4. \(P = t^2 + 3t + tu^3\)
    5. \( w=e^y\cos(x)+z^2\)
    Answers:
    1. \( dz = 3x^2\,dx +3y^2\,dy \)
    2. \( dz = ye^{xy}\,dx +xe^{xy}\,dy \)
    3. \( dz = -y\sin x\,dx +(\cos x + \cos y)\,dy \)
    4. \( dP = (2t + 3 + u^3)\, dt + 3t u^2 \,du \)
    5. \( dw = -e^y\sin(x)\,dx +e^y\cos(x)\,dy +2z\,dz\)

    32) a. Find the total differential \(dz\) of the function \( z=\dfrac{xy}{y+x}\) and then
    b. State its value where \( x\) changes from \( 10\) to \( 10.5\) and \( y\) changes from \( 15\) to \( 13\).

    Answer
    a. \( dz = \dfrac{y^2}{(x+y)^2}\, dx + \dfrac{x^2}{(x+y)^2} \,dy \)
    b. \(dx = 0.5\) and \(dy = -2\) so

    \( \begin{align*} dz &= f_x(10, 15) \, dx + f_y(10,15)\, dy \\
    &= \frac{15^2}{25^2}\,dx + \frac{10^2}{25^2}\, dy \\
    &= \frac{225}{625}\, (0.5) + \frac{100}{625} (-2) \\
    &= \frac{9}{25}\left(\frac{1}{2}\right) + \frac{4}{25} (-2) \\
    &= \frac{18}{100} - \frac{32}{100} \\
    &= .18 - .32 = -0.14 \end{align*}\)

    33) Let \( z=f(x,y)=xe^y.\) State its total differential. Then compute \( Δz\) from \( P(1,2)\) to \( Q(1.05,2.1)\) and then find the approximate change in \( z\), \(dz\), from point \( P\) to point \( Q\). Recall \( Δz=f(x+Δx,y+Δy)−f(x,y)\), and \( dz\) and \( Δz\) should be approximately equal, if \(dx\) and \(dy\) are both reasonably small.

    Answer
    Total Differential: \(dz = e^y\,dx + xe^y\, dy \)
    \( Δz≈1.185422\) and \( dz≈1.108.\) Note that they are relatively close.

    34) The volume of a right circular cylinder is given by \( V(r,h)=πr^2h.\) Find the differential \( dV\). Interpret the formula geometrically.

    Answer
    \( dV = 2 \pi r h\, dr + \pi r^2 \,dh \)

    35) See the preceding problem. Use differentials to estimate the amount of aluminum in an enclosed aluminum can with diameter \( 8.0cm\) and height \( 12cm\) if the aluminum is \( 0.04\) cm thick.

    Answer
    \( 16\,\text{cm}^3\)

    36) Use the differential \( dz\) to approximate the change in \( z=\sqrt{4−x^2−y^2}\) as \( (x,y)\) moves from point \( (1,1)\) to point \( (1.01,0.97).\) Compare this approximation with the actual change in the function.

    37) Let \( z=f(x,y)=x^2+3xy−y^2.\) Find the exact change in the function and the approximate change in the function as \( x\) changes from \( 2.00\) to \( 2.05\) and \( y\) changes from \( 3.00\) to \( 2.96\).

    Answer
    \( Δz=\) exact change \( =0.6449\), approximate change is \( dz=0.65\). The two values are close.

    38) The centripetal acceleration of a particle moving in a circle is given by \( a(r,v)=\frac{v^2}{r},\) where \( v\) is the velocity and \( r\) is the radius of the circle. Approximate the maximum percent error in measuring the acceleration resulting from errors of \( 3\%\) in \( v\) and \( 2\%\) in \( r\). (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in a is given by \( \frac{da}{a}\).)

    39) The radius \( r\) and height \( h\) of a right circular cylinder are measured with possible errors of \( 4\%\) and \( 5\%\), respectively. Approximate the maximum possible percentage error in measuring the volume (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in \( V\) is given by \( \frac{dV}{V}\).)

    Answer
    \( 13\%\) or \( 0.13\)

    40) The base radius and height of a right circular cone are measured as \( 10\) in. and \( 25\) in., respectively, with a possible error in measurement of as much as \( 0.1\) in. each. Use differentials to estimate the maximum error in the calculated volume of the cone.

    41) The electrical resistance \( R\) produced by wiring resistors \( R_1\) and \( R_2\) in parallel can be calculated from the formula \( \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}\). If \( R_1\) and \( R_2\) are measured to be \( 7Ω\) and \( 6Ω\), respectively, and if these measurements are accurate to within \( 0.05Ω\), estimate the maximum possible error in computing \( R\). (The symbol \( Ω\) represents an ohm, the unit of electrical resistance.)

    Answer
    \( 0.025\)

    42) The area of an ellipse with axes of length \( 2a\) and \( 2b\) is given by the formula \( A=πab\). Approximate the percent change in the area when \( a\) increases by \( 2\%\) and \( b\) increases by \( 1.5\%.\)

    43) The period \( T\) of a simple pendulum with small oscillations is calculated from the formula \( T=2π\sqrt{\frac{L}{g}}\), where \( L\) is the length of the pendulum and \( g\) is the acceleration resulting from gravity. Suppose that \( L\) and \( g\) have errors of, at most, \( 0.5\%\) and \( 0.1\%\), respectively. Use differentials to approximate the maximum percentage error in the calculated value of \( T\).

    Answer
    \( 0.3\%\)

    44) Electrical power \( P\) is given by \( P=\frac{V^2}{R}\), where \( V\) is the voltage and \( R\) is the resistance. Approximate the maximum percentage error in calculating power if \( 120 V\) is applied to a \( 2000−Ω\) resistor and the possible percent errors in measuring \( V\) and \( R\) are \( 3\%\) and \( 4\%\), respectively.

    For exercises 45 - 49, find the linear approximation of each function at the indicated point.

    45) \( f(x,y)=x\sqrt{y},\quad P(1,4)\)

    Answer
    \( L(x,y) = 2x+\frac{1}{4}y−1\)

    46) \( f(x,y)=e^x\cos y;\quad P(0,0)\)

    47) \( f(x,y)=\arctan(x+2y),\quad P(1,0)\)

    Answer
    \( L(x,y) = \frac{1}{2}x+y+\frac{1}{4}π−\frac{1}{2}\)

    48) \( f(x,y)=\sqrt{20−x^2−7y^2},\quad P(2,1)\)

    49) \( f(x,y,z)=\sqrt{x^2+y^2+z^2},\quad P(3,2,6)\)

    Answer
    \( L(x,y,z) = \frac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z\)

    50) [T] Find the equation of the tangent plane to the surface \( f(x,y)=x^2+y^2\) at point \( (1,2,5),\) and graph the surface and the tangent plane at the point.

    51) [T] Find the equation for the tangent plane to the surface at the indicated point, and graph the surface and the tangent plane: \( z=\ln(10x^2+2y^2+1),\quad P(0,0,0).\)

    Answer

    \( z=0\)

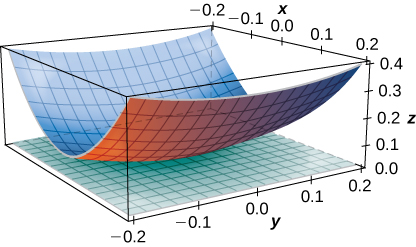
    Surface representing the function z=ln(10x^2+2y^2+1) and its tangent plane at the point (0, 0)

    52) [T] Find the equation of the tangent plane to the surface \( z=f(x,y)=\sin(x+y^2)\) at point \( \left(\frac{π}{4},0,\frac{\sqrt{2}}{2}\right)\), and graph the surface and the tangent plane.

    Contributors

    • Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

    • Paul Seeburger (Monroe Community College) created all but part e of exercise 31.

     

    Tangent Planes, Linear Approximations, and the Total Differential (Exercises) is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by LibreTexts.