2.3: Evaluate, Simplify, and Translate Expressions (Part 1)
- Last updated
- Save as PDF
- Page ID
- 21669
Learning Objectives
- Evaluate algebraic expressions
- Identify terms, coefficients, and like terms
- Simplify expressions by combining like terms
- Translate word phrases to algebraic expressions
Be prepared!
Before you get started, take this readiness quiz.
- Is \(n ÷ 5\) an expression or an equation? If you missed this problem, review Example 2.1.4.
- Simplify \(4^5\). If you missed this problem, review Example 2.1.6.
- Simplify \(1 + 8 • 9\). If you missed this problem, review Example 2.1.8.
Evaluate Algebraic Expressions
In the last section, we simplified expressions using the order of operations. In this section, we’ll evaluate expressions—again following the order of operations.
To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number. To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
Example \(\PageIndex{1}\): evaluate
Evaluate \(x + 7\) when
- \(x = 3\)
- \(x = 12\)
Solution
- To evaluate, substitute \(3\) for \(x\) in the expression, and then simplify.
| \(x + 7\) | |
| Substitute. | \(\textcolor{red}{3} + 7\) |
| Add. | \(10\) |
When \(x = 3\), the expression \(x + 7\) has a value of \(10\).
- To evaluate, substitute \(12\) for \(x\) in the expression, and then simplify.
| \(x + 7\) | |
| Substitute. | \(\textcolor{red}{12} + 7\) |
| Add. | \(19\) |
When \(x = 12\), the expression \(x + 7\) has a value of \(19\). Notice that we got different results for parts (a) and (b) even though we started with the same expression. This is because the values used for \(x\) were different. When we evaluate an expression, the value varies depending on the value used for the variable.
exercise \(\PageIndex{1}\)
Evaluate: \(y + 4\) when
- \(y = 6\)
- \(y = 15\)
- Answer a
-
\(10\)
- Answer b
-
\(19\)
exercise \(\PageIndex{2}\)
Evaluate: \(a − 5\) when
- \(a = 9\)
- \(a = 17\)
- Answer a
-
\(4\)
- Answer b
-
\(12\)
Example \(\PageIndex{2}\)
Evaluate \(9x − 2\), when
- \(x = 5\)
- \(x = 1\)
Solution
Remember \(ab\) means \(a\) times \(b\), so \(9x\) means \(9\) times \(x\).
- To evaluate the expression when \(x = 5\), we substitute \(5\) for \(x\), and then simplify.
| \(9x - 2\) | |
| Substitute \(\textcolor{red}{5}\) for x. | \(9 \cdot \textcolor{red}{5} - 2\) |
| Multiply. | \(45 - 2\) |
| Subtract. | \(43\) |
- To evaluate the expression when \(x = 1\), we substitute \(1\) for \(x\), and then simplify.
| \(9x - 2\) | |
| Substitute \(\textcolor{red}{1}\) for x. | \(9 \cdot \textcolor{red}{1} - 2\) |
| Multiply. | \(9 - 2\) |
| Subtract. | \(7\) |
Notice that in part (a) that we wrote \(9 • 5\) and in part (b) we wrote \(9(1)\). Both the dot and the parentheses tell us to multiply.
exercise \(\PageIndex{3}\)
Evaluate: \(8x − 3\), when
- \(x = 2\)
- \(x = 1\)
- Answer a
-
\(13\)
- Answer b
-
\(5\)
exercise \(\PageIndex{4}\)
Evaluate: \(4y − 4\), when
- \(y = 3\)
- \(y = 5\)
- Answer a
-
\(8\)
- Answer b
-
\(16\)
Example \(\PageIndex{3}\): evaluate
Evaluate \(x^2\) when \(x = 10\).
Solution
We substitute \(10\) for \(x\), and then simplify the expression.
| \(x^{2}\) | |
| Substitute \(\textcolor{red}{10}\) for x. | \(\textcolor{red}{10}^{2}\) |
| Use the definition of exponent. | \(10 \cdot 10\) |
| Multiply | \(100\) |
When \(x = 10\), the expression \(x^2\) has a value of \(100\).
exercise \(\PageIndex{5}\)
Evaluate: \(x^2\) when \(x = 8\).
- Answer
-
\(64\)
exercise \(\PageIndex{6}\)
Evaluate: \(x^3\) when \(x = 6\).
- Answer
-
\(216\)
Example \(\PageIndex{4}\): evaluate
Evaluate \(2^x\) when \(x = 5\).
Solution
In this expression, the variable is an exponent.
| \(2^{x}\) | |
| Substitute \(\textcolor{red}{5}\) for x. | \(2^{\textcolor{red}{5}}\) |
| Use the definition of exponent. | \(2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) |
| Multiply | \(32\) |
When \(x = 5\), the expression \(2^x\) has a value of \(32\).
exercise \(\PageIndex{7}\)
Evaluate: \(2^x\) when \(x = 6\).
- Answer
-
\(64\)
exercise \(\PageIndex{8}\)
Evaluate: \(3^x\) when \(x = 4\).
- Answer
-
\(81\)
Example \(\PageIndex{5}\): evaluate
Evaluate \(3x + 4y − 6\) when \(x = 10\) and \(y = 2\).
Solution
This expression contains two variables, so we must make two substitutions.
| \(3x + 4y − 6\) | |
| Substitute \(\textcolor{red}{10}\) for x and \(\textcolor{blue}{2}\) for y. | \(3(\textcolor{red}{10}) + 4(\textcolor{blue}{2}) − 6\) |
| Multiply. | \(30 + 8 - 6\) |
| Add and subtract left to right. | \(32\) |
When \(x = 10\) and \(y = 2\), the expression \(3x + 4y − 6\) has a value of \(32\).
exercise \(\PageIndex{9}\)
Evaluate: \(2x + 5y − 4\) when \(x = 11\) and \(y = 3\)
- Answer
-
\(33\)
exercise \(\PageIndex{10}\)
Evaluate: \(5x − 2y − 9\) when \(x = 7\) and \(y = 8\)
- Answer
-
\(10\)
Example \(\PageIndex{6}\): evaluate
Evaluate \(2x^2 + 3x + 8\) when \(x = 4\).
Solution
We need to be careful when an expression has a variable with an exponent. In this expression, \(2x^2\) means \(2 • x • x\) and is different from the expression \((2x)^2\), which means \(2x • 2x\).
| \(2x^{2} + 3x + 8\) | |
| Substitute \(\textcolor{red}{4}\) for each x. | \(2(\textcolor{red}{4})^{2} + 3(\textcolor{red}{4}) + 8\) |
| Simplify 42. | \(2(16) + 3(4) + 8\) |
| Multiply. | \(32 + 12 + 8\) |
| Add. | \(52\) |
exercise \(\PageIndex{11}\)
Evaluate: \(3x^2 + 4x + 1\) when \(x = 3\).
- Answer
-
\(40\)
exercise \(\PageIndex{12}\)
Evaluate: \(6x^2 − 4x − 7\) when \(x = 2\).
- Answer
-
\(9\)
Identify Terms, Coefficients, and Like Terms
Algebraic expressions are made up of terms. A term is a constant or the product of a constant and one or more variables. Some examples of terms are \(7\), \(y\), \(5x^2\), \(9a\), and \(13xy\).
The constant that multiplies the variable(s) in a term is called the coefficient. We can think of the coefficient as the number in front of the variable. The coefficient of the term \(3x\) is \(3\). When we write \(x\), the coefficient is \(1\), since \(x = 1 • x\). Table \(\PageIndex{1}\) gives the coefficients for each of the terms in the left column.
| Term | Coefficient |
|---|---|
| 7 | 7 |
| 9a | 9 |
| y | 1 |
| 5x2 | 5 |
An algebraic expression may consist of one or more terms added or subtracted. In this chapter, we will only work with terms that are added together. Table \(\PageIndex{2}\) gives some examples of algebraic expressions with various numbers of terms. Notice that we include the operation before a term with it.
| Expression | Terms |
|---|---|
| 7 | 7 |
| y | y |
| x + 7 | x, 7 |
| 2x + 7y + 4 | 2x, 7y, 4 |
| 3x2 + 4x2 + 5y + 3 | 3x2, 4x2, 5y, 3 |
Example \(\PageIndex{7}\):
Identify each term in the expression \(9b + 15x^2 + a + 6\). Then identify the coefficient of each term.
Solution
The expression has four terms. They are \(9b\), \(15x^2\), \(a\), and \(6\).
The coefficient of \(9b\) is \(9\).
The coefficient of \(15x^2\) is \(15\).
Remember that if no number is written before a variable, the coefficient is \(1\). So the coefficient of a is \(1\).
The coefficient of a constant is the constant, so the coefficient of \(6\) is \(6\).
exercise \(\PageIndex{13}\)
Identify all terms in the given expression, and their coefficients: \(4x + 3b + 2\)
- Answer
-
The terms are \(4x, 3b,\) and \(2\). The coefficients are \(4, 3,\) and \(2\).
exercise \(\PageIndex{14}\)
Identify all terms in the given expression, and their coefficients: \(9a + 13a^2 + a^3\)
- Answer
-
The terms are \(9a, 13a^2,\) and \(a^3\), The coefficients are \(9, 13,\) and \(1\).
Some terms share common traits. Look at the following terms. Which ones seem to have traits in common?
\(5x, 7, n^{2}, 4, 3x, 9n^{2}\)
Which of these terms are like terms?
- The terms \(7\) and \(4\) are both constant terms.
- The terms \(5x\) and \(3x\) are both terms with \(x\).
- The terms \(n^2\) and \(9n^2\) both have \(n^2\).
Terms are called like terms if they have the same variables and exponents. All constant terms are also like terms. So among the terms \(5x, 7, n^2, 4, 3x, 9n^2, 7\) and \(4\) are like terms, \(5x\) and \(3x\) are like terms, and \(n^2\) and \(9n^2\) are like terms.
Definition: Like terms
Terms that are either constants or have the same variables with the same exponents are like terms.
Example \(\PageIndex{8}\): identify
Identify the like terms:
- \(y^3, 7x^2, 14, 23, 4y^3, 9x, 5x^2\)
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Solution
- \(y^3, 7x^2, 14, 23, 4y^3, 9x, 5x^2\)
Look at the variables and exponents. The expression contains \(y^3, x^2, x\), and constants. The terms \(y^3\) and \(4y^3\) are like terms because they both have \(y^3\). The terms \(7x^2\) and \(5x^2\) are like terms because they both have \(x^2\). The terms \(14\) and \(23\) are like terms because they are both constants. The term \(9x\) does not have any like terms in this list since no other terms have the variable \(x\) raised to the power of \(1\).
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Look at the variables and exponents. The expression contains the terms \(4x^2, 2x, 5x^2, 6x, 40x\), and \(8xy\) The terms \(4x^2\) and \(5x^2\) are like terms because they both have \(x^2\). The terms \(2x, 6x\), and \(40x\) are like terms because they all have \(x\). The term \(8xy\) has no like terms in the given expression because no other terms contain the two variables \(xy\).
exercise \(\PageIndex{15}\)
Identify the like terms in the list or the expression: \(9, 2x^3, y^2, 8x^3, 15, 9y, 11y^2\)
- Answer
-
\(9, 15\); \(2x^3\) and \(8x^3\), \(y^2\), and \(11y^2\)
exercise \(\PageIndex{16}\)
Identify the like terms in the list or the expression: \(4x^3 + 8x^2 + 19 + 3x^2 + 24 + 6x^3\)
- Answer
-
\(4x^3\) and \(6x^3\); \(8x^2\) and \(3x^2\); \(19\) and \(24\)
Simplify Expressions by Combining Like Terms
We can simplify an expression by combining the like terms. What do you think \(3x + 6x\) would simplify to? If you thought \(9x\), you would be right!
We can see why this works by writing both terms as addition problems.
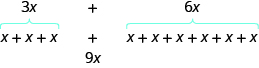
Add the coefficients and keep the same variable. It doesn’t matter what \(x\) is. If you have \(3\) of something and add \(6\) more of the same thing, the result is \(9\) of them. For example, \(3\) oranges plus \(6\) oranges is \(9\) oranges. We will discuss the mathematical properties behind this later.
The expression \(3x + 6x\) has only two terms. When an expression contains more terms, it may be helpful to rearrange the terms so that like terms are together. The Commutative Property of Addition says that we can change the order of addends without changing the sum. So we could rearrange the following expression before combining like terms.
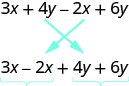
Now it is easier to see the like terms to be combined.
HOW TO: COMBINE LIKE TERMS
Step 1. Identify like terms.
Step 2. Rearrange the expression so like terms are together.
Step 3. Add the coefficients of the like terms.
Example \(\PageIndex{9}\): simplify
Simplify the expression: \(3x + 7 + 4x + 5\).
Solution
| \(3x + 7 + 4x + 5\) | |
| Identify the like terms | \(\textcolor{red}{3x} + \textcolor{blue}{7} + \textcolor{red}{4x} + \textcolor{blue}{5}\) |
| Rearrange the expression, so the like terms are together. | \(\textcolor{red}{3x} + \textcolor{red}{4x} + \textcolor{blue}{7} + \textcolor{blue}{5}\) |
| Add the coefficients of the like terms. | \(\textcolor{red}{7x} + \textcolor{blue}{12}\) |
| The original expression is simplified to... | \(7x + 12\) |
exercise \(\PageIndex{17}\)
Simplify: \(7x + 9 + 9x + 8\)
- Answer
-
\(16x+17\)
exercise \(\PageIndex{18}\)
Simplify: \(5y + 2 + 8y + 4y + 5\)
- Answer
-
\(17y+7\)
Example \(\PageIndex{10}\): simplify
Simplify the expression: \(7x^2 + 8x + x^2 + 4x\).
Solution
| \(7x^{2} + 8x + x^{2} + 4x\) | |
| Identify the like terms. | \(\textcolor{red}{7x^{2}} + \textcolor{blue}{8x} + \textcolor{red}{x^{2}} + \textcolor{blue}{4x}\) |
| Rearrange the expression so like terms are together. | \(\textcolor{red}{7x^{2}} + \textcolor{red}{x^{2}} + \textcolor{blue}{8x} + \textcolor{blue}{4x}\) |
| Add the coefficients of the like terms. | \(\textcolor{red}{8x^{2}} + \textcolor{blue}{12x}\) |
These are not like terms and cannot be combined. So \(8x^2 + 12x\) is in simplest form.
exercise \(\PageIndex{19}\)
Simplify: \(3x^2 + 9x + x^2 + 5x\)
- Answer
-
\(4x^2+14x\)
exercise \(\PageIndex{20}\)
Simplify: \(11y^2 + 8y + y^2 + 7y\)
- Answer
-
\(12y^2+15y\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


