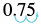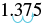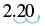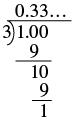6.1: Understand Percent
- Page ID
- 21725
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use the definition of percent
- Convert percents to fractions and decimals
- Convert decimals and fractions to percents
Before you get started, take this readiness quiz.
- Translate “the ratio of 33 to 5” into an algebraic expression. If you missed this problem, review Table 2.4.3.
- Write 3 5 as a decimal. If you missed this problem, review Example 5.5.1.
- Write 0.62 as a fraction. If you missed this problem, review Example 5.1.4.
Use the Definition of Percent
How many cents are in one dollar? There are 100 cents in a dollar. How many years are in a century? There are 100 years in a century. Does this give you a clue about what the word “per cent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is 100. We use the percent symbol %, to show percent.
A percent is a ratio whose denominator is 100.
According to data from the American Association of Community Colleges (2015), about 57% of community college students are female. This means 57 out of every 100 community college students are female, as Figure \(\PageIndex{1}\) shows. Out of the 100 squares on the grid, 57 are shaded, which we write as the ratio \(\dfrac{57}{100}\).
Figure \(\PageIndex{1}\) - Among every 100 community college students, 57 are female.
Similarly, 25% means a ratio of \(\dfrac{25}{100}\), 3% means a ratio of \(\dfrac{3}{100}\) and 100% means a ratio of \(\dfrac{100}{100}\). In words, "one hundred percent" means the total 100% is \(\dfrac{100}{100}\), and since \(\dfrac{100}{100}\) = 1, we see that 100% means 1 whole.
According to the Public Policy Institute of California (2010), 44% of parents of public school children would like their youngest child to earn a graduate degree. Write this percent as a ratio.
Solution
| The amount we want to convert is 44%. | 44% |
| Write the percent as a ratio. Remember that percent means per 100. | $$\dfrac{44}{100}$$ |
Write the percent as a ratio. According to a survey, 89% of college students have a smartphone.
- Answer
-
\(\frac{89}{100}\)
Write the percent as a ratio. A study found that 72% of U.S. teens send text messages regularly.
- Answer
-
\(\frac{72}{100}\)
In 2007, according to a U.S. Department of Education report, 21 out of every 100 first-time freshmen college students at 4-year public institutions took at least one remedial course. Write this as a ratio and then as a percent.
Solution
| The amount we want to convert is 21 out of 100. | 21 out of 100 |
| Write as a ratio. | $$\dfrac{21}{100}$$ |
| Convert the 21 per 100 to percent. | 21% |
Write as a ratio and then as a percent: The American Association of Community Colleges reported that 62 out of 100 full-time community college students balance their studies with full-time or part time employment.
- Answer
-
\(\frac{62}{100}\), 62%
Write as a ratio and then as a percent: In response to a student survey, 41 out of 100 Santa Ana College students expressed a goal of earning an Associate's degree or transferring to a four-year college.
- Answer
-
\(\frac{41}{100}\), 41%
Convert Percents to Fractions and Decimals
Since percents are ratios, they can easily be expressed as fractions. Remember that percent means per 100, so the denominator of the fraction is 100.
Step 1. Write the percent as a ratio with the denominator 100.
Step 2. Simplify the fraction if possible.
Convert each percent to a fraction: (a) 36% (b) 125%
Solution
(a) 36%
| Write as a ratio with denominator 100. | $$\dfrac{36}{100}$$ |
| Simplify. | $$\dfrac{9}{25}$$ |
(b) 125%
| Write as a ratio with denominator 100. | $$\dfrac{125}{100}$$ |
| Simplify. | $$\dfrac{5}{4}$$ |
Convert each percent to a fraction: (a) 48% (b) 110%
- Answer a
-
\(\frac{12}{25}\)
- Answer b
-
\(\frac{11}{10}\)
Convert each percent to a fraction: (a) 64% (b) 150%
- Answer a
-
\(\frac{16}{25}\)
- Answer b
-
\(\frac{3}{2}\)
The previous example shows that a percent can be greater than 1. We saw that 125% means \(\dfrac{125}{100}\), or \(\dfrac{5}{4}\). These are improper fractions, and their values are greater than one.
Convert each percent to a fraction: (a) 24.5% (b) 33 \(\dfrac{1}{3}\)%
Solution
(a) 24.5%
| Write as a ratio with denominator 100. | $$\dfrac{24.5}{100}$$ |
| Clear the decimal by multiplying numerator and denominator by 10. | $$\dfrac{24.5(10)}{100(10)}$$ |
| Multiply. | $$\dfrac{245}{1000}$$ |
| Rewrite showing common factors. | $$\dfrac{5 \cdot 49}{5 \cdot 200}$$ |
| Simplify. | $$\dfrac{49}{200}$$ |
(b) 33 \(\dfrac{1}{3}\)%
| Write as a ratio with denominator 100. | $$\dfrac{33 \dfrac{1}{3}}{100}$$ |
| Write the numerator as an improper fraction. | $$\dfrac{\dfrac{100}{3}}{100}$$ |
| Rewrite as fraction division, replacing 100 with \(\dfrac{100}{1}\). | $$\dfrac{100}{3} \div \dfrac{100}{1}$$ |
| Multiply by the reciprocal. | $$\dfrac{100}{3} \cdot \dfrac{1}{100}$$ |
| Simplify. | $$\dfrac{1}{3}$$ |
Convert each percent to a fraction: (a) 64.4% (b) 66\(\dfrac{2}{3}\)%
- Answer a
-
\(\frac{161}{250}\)
- Answer b
-
\(\frac{2}{3}\)
Convert each percent to a fraction: (a) 42.5% (b) 8\(\dfrac{3}{4}\)%
- Answer a
-
\(\frac{113}{250}\)
- Answer b
-
\(\frac{7}{80}\)
In Decimals, we learned how to convert fractions to decimals. To convert a percent to a decimal, we first convert it to a fraction and then change the fraction to a decimal.
Step 1. Write the percent as a ratio with the denominator 100.
Step 2. Convert the fraction to a decimal by dividing the numerator by the denominator.
Convert each percent to a decimal: (a) 6% (b) 78%
Solution
Because we want to change to a decimal, we will leave the fractions with denominator 100 instead of removing common factors.
(a) 6%
| Write as a ratio with denominator 100. | $$\dfrac{6}{100}$$ |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.06 |
(b) 78%
| Write as a ratio with denominator 100. | $$\dfrac{78}{100}$$ |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.78 |
Convert each percent to a decimal: (a) 9% (b) 87%
- Answer a
-
\(0.09\)
- Answer b
-
\(0.87\)
Convert each percent to a decimal: (a) 3% (b) 91%
- Answer a
-
\(0.03\)
- Answer b
-
\(0.91\)
Convert each percent to a decimal: (a) 135% (b) 12.5%
Solution
| Write as a ratio with denominator 100. | $$\dfrac{135}{100}$$ |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 1.35 |
(b) 12.5%
| Write as a ratio with denominator 100. | $$\dfrac{12.5}{100}$$ |
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.125 |
Convert each percent to a decimal: (a) 115% (b) 23.5%
- Answer a
-
\(1.15\)
- Answer b
-
\(0.235\)
Convert each percent to a decimal: (a) 123% (b) 16.8%
- Answer a
-
\(1.23\)
- Answer b
-
\(0.168\)
Let's summarize the results from the previous examples in Table \(\PageIndex{1}\), and look for a pattern we could use to quickly convert a percent number to a decimal number.
| Percent | Decimal |
|---|---|
| 6% | 0.06 |
| 78% | 0.78 |
| 135% | 1.35 |
| 12.5% | 0.125 |
Do you see the pattern? To convert a percent number to a decimal number, we move the decimal point two places to the left and remove the % sign. (Sometimes the decimal point does not appear in the percent number, but just like we can think of the integer 6 as 6.0, we can think of 6% as 6.0%.) Notice that we may need to add zeros in front of the number when moving the decimal to the left.
Figure \(\PageIndex{2}\) uses the percents in Table \(\PageIndex{1}\) and shows visually how to convert them to decimals by moving the decimal point two places to the left.
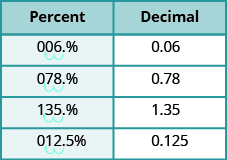
Figure \(\PageIndex{2}\)
Among a group of business leaders, 77% believe that poor math and science education in the U.S. will lead to higher unemployment rates. Convert the percent to: (a) a fraction (b) a decimal
Solution
(a)
| Write as a ratio with denominator 100. | $$\dfrac{77}{100}$$ |
(b)
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.77 |
Twitter's share of web traffic jumped 24% when one celebrity tweeted live on air. Convert the percent to: (a) a fraction and (b) a decimal.
- Answer a
-
\(\frac{6}{25}\)
- Answer b
-
\(0.24\)
The U.S. Census estimated that in 2013, 44% of the population of Boston age 25 or older have a bachelor's or higher degrees. Convert the percent to: (a) a fraction and (b) a decimal.
- Answer a
-
\(\frac{22}{50}\)
- Answer b
-
\(0.44\)
There are four suits of cards in a deck of cards—hearts, diamonds, clubs, and spades. The probability of randomly choosing a heart from a shuffled deck of cards is 25%. Convert the percent to: (a) a fraction (b) a decimal.
Figure \(\PageIndex{3}\) - (credit: Riles32807, Wikimedia Commons)
Solution
(a)
| Write as a ratio with denominator 100. | $$\dfrac{25}{100}$$ |
| Simplify. | $$\dfrac{1}{4}$$ |
(b)
| Change the fraction to a decimal by dividing the numerator by the denominator. | 0.25 |
The probability that it will rain Monday is 30%. Convert the percent to: (a) a fraction, and (b) a decimal.
- Answer a
-
\(\frac{3}{10}\)
- Answer b
-
\(0.3\)
The probability of getting heads three times when tossing a coin three times is 12.5%. Convert the percent to: (a) a fraction, and (b) a decimal.
- Answer a
-
\(\frac{12.5}{100}\)
- Answer b
-
\(0.125\)
Convert Decimals and Fractions to Percents
To convert a decimal to a percent, remember that percent means per hundred. If we change the decimal to a fraction whose denominator is 100, it is easy to change that fraction to a percent.
Step 1. Write the decimal as a fraction.
Step 2. If the denominator of the fraction is not 100, rewrite it as an equivalent fraction with denominator 100.
Step 3. Write this ratio as a percent.
Convert each decimal to a percent: (a) 0.05 (b) 0.83
Solution
(a) 0.05
| Write as a fraction. The denominator is 100. | $$\dfrac{5}{100}$$ |
| Write this ratio as a percent. | 5% |
(b)
| The denominator is 100. | $$\dfrac{83}{100}$$ |
| Write this ratio as a percent. | 83% |
Convert each decimal to a percent: (a) 0.01 (b) 0.17.
- Answer a
-
1%
- Answer b
-
17%
Convert each decimal to a percent: (a) 0.04 (b) 0.41.
- Answer a
-
4%
- Answer b
-
41%
To convert a mixed number to a percent, we first write it as an improper fraction.
Convert each decimal to a percent: (a) 1.05 (b) 0.075
Solution
(a) 1.05
| Write as a fraction. | $$1 \dfrac{5}{100}$$ |
| Write as an improper fraction. The denominator is 100. | $$\dfrac{105}{100}$$ |
| Write this ratio as a percent. | 105% |
Notice that since 1.05 > 1, the result is more than 100%.
(b) 0.075
| Write as a fraction. | $$\dfrac{75}{1,000}$$ |
| Divide the numerator and denominator by 10, so that the denominator is 100. | $$\dfrac{7.5}{100}$$ |
| Write this ratio as a percent. | 7.5% |
Convert each decimal to a percent: (a) 1.75 (b) 0.0825
- Answer a
-
175%
- Answer b
-
8.25%
Convert each decimal to a percent: (a) 2.25 (b) 0.0925
- Answer a
-
225%
- Answer b
-
9.25%
Let's summarize the results from the previous examples in Table 6.20 so we can look for a pattern.
| Decimal | Percent |
|---|---|
| 0.05 | 5% |
| 0.83 | 83% |
| 1.05 | 105% |
| 0.075 | 7.5% |
Do you see the pattern? To convert a decimal to a percent, we move the decimal point two places to the right and then add the percent sign.
Figure \(\PageIndex{4}\) uses the decimal numbers in Table \(\PageIndex{2}\) and shows visually to convert them to percents by moving the decimal point two places to the right and then writing the % sign.
Figure \(\PageIndex{4}\)
In Decimals, we learned how to convert fractions to decimals. Now we also know how to change decimals to percents. So to convert a fraction to a percent, we first change it to a decimal and then convert that decimal to a percent.
Step 1. Convert the fraction to a decimal.
Step 2. Convert the decimal to a percent.
Convert each fraction or mixed number to a percent: (a) \(\dfrac{3}{4}\) (b) \(\dfrac{11}{8}\) (c) \(2 \dfrac{1}{5}\)
Solution
To convert a fraction to a decimal, divide the numerator by the denominator.
(a)
| Change to a decimal. | $$\dfrac{3}{4}$$ |
| Write as a percent by moving the decimal two places. |  |
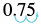| 75% |
(b)
| Change to a decimal. | $$\dfrac{11}{8}$$ |
| Write as a percent by moving the decimal two places. |  |
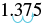| 137.5% |
(c)
| Write as an improper fraction. | $$2 \dfrac{1}{5}$$ |
| Change to a decimal. | $$\dfrac{11}{5}$$ |
| Write as a percent. |  |
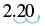| 220% |
Notice that we needed to add zeros at the end of the number when moving the decimal two places to the right.
Convert each fraction or mixed number to a percent: (a) \(\dfrac{5}{8}\) (b) \(\dfrac{11}{4}\) (c) \(3 \dfrac{2}{5}\)
- Answer a
-
62.5%
- Answer b
-
275%
- Answer c
-
340%
Convert each fraction or mixed number to a percent: (a) \(\dfrac{7}{8}\) (b) \(\dfrac{9}{4}\) (c) \(1 \dfrac{3}{5}\)
- Answer a
-
87.5%
- Answer b
-
225%
- Answer c
- 160%
Sometimes when changing a fraction to a decimal, the division continues for many decimal places and we will round off the quotient. The number of decimal places we round to will depend on the situation. If the decimal involves money, we round to the hundredths place. For most other cases in this book we will round the number to the nearest thousandth, so the percent will be rounded to the nearest tenth.
Convert \(\dfrac{5}{7}\) to a percent.
Solution
To change a fraction to a decimal, we divide the numerator by the denominator.
| Change to a decimal—rounding to the nearest thousandth. | 0.714 |
| Write as a percent. | 71.4% |
Convert the fraction to a percent: \(\dfrac{3}{7}\)
- Answer
- 42.9%
Convert the fraction to a percent: \(\dfrac{4}{7}\)
- Answer
-
57.1%
When we first looked at fractions and decimals, we saw that fractions converted to a repeating decimal. When we converted the fraction \(\dfrac{4}{3}\) to a decimal, we wrote the answer as 1.\(\overline{3}\). We will use this same notation, as well as fraction notation, when we convert fractions to percents in the next example.
An article in a medical journal claimed that approximately \(\dfrac{1}{3}\) of American adults are obese. Convert the fraction \(\dfrac{1}{3}\) to a percent.
Solution
| Change to a decimal. |  |
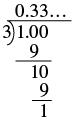| Write as a repeating decimal. | 0.333 … |
| Write as a percent. | \(33 \dfrac{1}{3}\)% |
We could also write the percent as 33.\(\overline{3}\)%.
According to the U.S. Census Bureau, about \(\dfrac{1}{9}\) of United States housing units have just 1 bedroom. Convert the fraction to a percent.
- Answer
-
\(11. \overline{1} \%\), or \(11 \frac{1}{9} \% \)
According to the U.S. Census Bureau, about \(\dfrac{1}{6}\) of Colorado residents speak a language other than English at home. Convert the fraction to a percent.
- Answer
-
\(16. \overline{6} \%\), or \(16 \frac{2}{3} \% \)
Practice Makes Perfect
Use the Definition of Percents
In the following exercises, write each percent as a ratio.
- In 2014, the unemployment rate for those with only a high school degree was 6.0%.
- In 2015, among the unemployed, 29% were long-term unemployed.
- The unemployment rate for those with Bachelor's degrees was 3.2% in 2014.
- The unemployment rate in Michigan in 2014 was 7.3%.
In the following exercises, write as (a) a ratio and (b) a percent.
- 57 out of 100 nursing candidates received their degree at a community college.
- 80 out of 100 firefighters and law enforcement officers were educated at a community college.
- 42 out of 100 first-time freshmen students attend a community college.
- 71 out of 100 full-time community college faculty have a master's degree.
Convert Percents to Fractions and Decimals
In the following exercises, convert each percent to a fraction and simplify all fractions.
- 4%
- 8%
- 17%
- 19%
- 52%
- 78%
- 125%
- 135%
- 37.5%
- 42.5%
- 18.4%
- 46.4%
- \(9 \dfrac{1}{2}\)%
- \(8 \dfrac{1}{2}\) %
- \(5 \dfrac{1}{3}\) %
- \(6 \dfrac{2}{3}\) %
In the following exercises, convert each percent to a decimal.
- 5%
- 9%
- 1%
- 2%
- 63%
- 71%
- 40%
- 50%
- 115%
- 125%
- 150%
- 250%
- 21.4%
- 39.3%
- 7.8%
- 6.4%
In the following exercises, convert each percent to (a) a simplified fraction and (b) a decimal.
- In 2010, 1.5% of home sales had owner financing. (Source: Bloomberg Businessweek, 5/ 23–29/2011)
- In 2000, 4.2% of the United States population was of Asian descent. (Source: www.census.gov)
- According to government data, in 2013 the number of cell phones in India was 70.23% of the population.
- According to the U.S. Census Bureau, among Americans age 25 or older who had doctorate degrees in 2014, 37.1% are women.
- A couple plans to have two children. The probability they will have two girls is 25%.
- Javier will choose one digit at random from 0 through 9. The probability he will choose 3 is 10%.
- According to the local weather report, the probability of thunderstorms in New York City on July 15 is 60%.
- A club sells 50 tickets to a raffle. Osbaldo bought one ticket. The probability he will win the raffle is 2%.
Convert Decimals and Fractions to Percents
In the following exercises, convert each decimal to a percent.
- 0.01
- 0.03
- 0.18
- 0.15
- 1.35
- 1.56
- 3
- 4
- 0.009
- 0.008
- 0.0875
- 0.0625
- 1.5
- 2.2
- 2.254
- 2.317
In the following exercises, convert each fraction to a percent.
- \(\dfrac{1}{4}\)
- \(\dfrac{1}{5}\)
- \(\dfrac{3}{8}\)
- \(\dfrac{5}{8}\)
- \(\dfrac{7}{4}\)
- \(\dfrac{9}{8}\)
- \(6 \dfrac{4}{5}\)
- \(5 \dfrac{1}{4}\)
- \(\dfrac{5}{12}\)
- \(\dfrac{11}{12}\)
- \(2 \dfrac{2}{3}\)
- \(1 \dfrac{2}{3}\)
- \(\dfrac{3}{7}\)
- \(\dfrac{6}{7}\)
- \(\dfrac{5}{9}\)
- \(\dfrac{4}{9}\)
In the following exercises, convert each fraction to a percent.
- \(\dfrac{1}{4}\) of washing machines needed repair.
- \(\dfrac{1}{5}\) of dishwashers needed repair.
In the following exercises, convert each fraction to a percent.
- According to the National Center for Health Statistics, in 2012, 7 20 of American adults were obese.
- The U.S. Census Bureau estimated that in 2013, 85% of Americans lived in the same house as they did 1 year before.
In the following exercises, complete the table.
-
Table 6.26
| Fraction | Decimal | Percent |
|---|---|---|
| $$\dfrac{1}{2}$$ | ||
| 0.45 | ||
| 18% | ||
| $$\dfrac{1}{3}$$ | ||
| 0.0008 | ||
| 2 |
-
Table 6.27
| Fraction | Decimal | Percent |
|---|---|---|
| $$\dfrac{1}{4}$$ | ||
| 0.65 | ||
| 22% | ||
| $$\dfrac{2}{3}$$ | ||
| 0.0004 | ||
| 3 |
Everyday Math
- Sales tax Felipa says she has an easy way to estimate the sales tax when she makes a purchase. The sales tax in her city is 9.05%. She knows this is a little less than 10%.
- Convert 10% to a fraction.
- Use your answer from (a) to estimate the sales tax Felipa would pay on a $95 dress.
- Savings Ryan has 25% of each paycheck automatically deposited in his savings account.
- Write 25% as a fraction.
- Use your answer from (a) to find the amount that goes to savings from Ryan's $2,400 paycheck.
- Amelio is shopping for textbooks online. He found three sellers that are offering a book he needs for the same price, including shipping. To decide which seller to buy from he is comparing their customer satisfaction ratings. The ratings are given in the chart.
| Seller | Rating |
|---|---|
| A | 4/5 |
| B | 3.5/4 |
| C | 85% |
- Write seller C’s rating as a fraction and a decimal.
- Write seller B’s rating as a percent and a decimal.
- Write seller A’s rating as a percent and a decimal.
- Which seller should Amelio buy from and why?
Writing Exercises
- Convert 25%, 50%, 75%, and 100% to fractions. Do you notice a pattern? Explain what the pattern is.
- Convert \(\dfrac{1}{10}, \dfrac{2}{10}, \dfrac{3}{10}, \dfrac{4}{10}, \dfrac{5}{10}, \dfrac{6}{10}, \dfrac{7}{10}, \dfrac{8}{10}\), and \(\dfrac{9}{10}\) to percents. Do you notice a pattern? Explain what the pattern is.
- When the Szetos sold their home, the selling price was 500% of what they had paid for the house 30 years ago. Explain what 500% means in this context.
- According to cnn.com, cell phone use in 2008 was 600% of what it had been in 2001. Explain what 600% means in this context.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."