7.2: Commutative and Associative Properties (Part 1)
- Last updated
- Save as PDF
- Page ID
- 21735
Learning Objectives
- Use the commutative and associative properties
- Evaluate expressions using the commutative and associative properties
- Simplify expressions using the commutative and associative properties
be prepared!
Before you get started, take this readiness quiz.
- Simplify: 7y + 2 + y + 13. If you missed this problem, review Example 2.3.10.
- Multiply: \(\dfrac{2}{3} \cdot 18\). If you missed this problem, review Example 4.3.10.
- Find the opposite of 15. If you missed this problem, review Example 3.1.3.
In the next few sections, we will take a look at the properties of real numbers. Many of these properties will describe things you already know, but it will help to give names to the properties and define them formally. This way we’ll be able to refer to them and use them as we solve equations in the next chapter.
Use the Commutative and Associative Properties
Think about adding two numbers, such as 5 and 3.
\[\begin{split} 5 &+ 3 \qquad 3 + 5 \\ &\; 8 \qquad \qquad 8 \end{split}\]
The results are the same. 5 + 3 = 3 + 5
Notice, the order in which we add does not matter. The same is true when multiplying 5 and 3.
\[\begin{split} 5 &\cdot 3 \qquad \; 3 \cdot 5 \\ & 15 \qquad \quad 15 \end{split}\]
Again, the results are the same! 5 • 3 = 3 • 5. The order in which we multiply does not matter. These examples illustrate the commutative properties of addition and multiplication.
Definition: Commutative Properties
Commutative Property of Addition: if a and b are real numbers, then a + b = b + a
Commutative Property of Multiplication: if a and b are real numbers, then a • b = b • a
The commutative properties have to do with order. If you change the order of the numbers when adding or multiplying, the result is the same.
Example \(\PageIndex{1}\):
Use the commutative properties to rewrite the following expressions: (a) −1 + 3 = _____ (b) 4 • 9 = _____
Solution
(a) −1 + 3 = _____
| Use the commutative property of addition to change the order. | −1 + 3 = 3 + (−1) |
(b) 4 • 9 = _____
| Use the commutative property of multiplication to change the order. | 4 • 9 = 9 • 4 |
Exercise \(\PageIndex{1}\):
Use the commutative properties to rewrite the following expressions: (a) −4 + 7 = _____ (b) 6 • 12 = _____
- Answer a
-
\(-4+7=7+(-4)\)
- Answer b
-
\(6 \cdot 12=12 \cdot 6\)
Exercise \(\PageIndex{2}\):
Use the commutative properties to rewrite the following expressions: (a) 14 + (-2) = _____ (b) 3(-5) = _____
- Answer a
-
\(14+(-2)=-2+14\)
- Answer b
-
\(3(-5)=(-5) 3\)
What about subtraction? Does order matter when we subtract numbers? Does 7 − 3 give the same result as 3 − 7?
\[\begin{split} 7 &- 3 \qquad 3 - 7 \\ &\; 4 \qquad \quad -4 \\ & \quad 4 \neq -4 \end{split}\]
The results are not the same. 7 − 3 ≠ 3 − 7
Since changing the order of the subtraction did not give the same result, we can say that subtraction is not commutative. Let’s see what happens when we divide two numbers. Is division commutative?
\[\begin{split} 12 &\div 4 \qquad 4 \div 12 \\ & \dfrac{12}{4} \qquad \quad \dfrac{4}{12} \\ &\; 3 \qquad \qquad \dfrac{1}{3} \\ &\quad \; 3 \neq \dfrac{1}{3} \end{split}\]
The results are not the same. So 12 ÷ 4 ≠ 4 ÷ 12
Since changing the order of the division did not give the same result, division is not commutative.
Addition and multiplication are commutative. Subtraction and division are not commutative.
Suppose you were asked to simplify this expression.
\[7 + 8 + 2\]
How would you do it and what would your answer be?
Some people would think 7 + 8 is 15 and then 15 + 2 is 17. Others might start with 8 + 2 makes 10 and then 7 + 10 makes 17.
Both ways give the same result, as shown in Figure \(\PageIndex{1}\). (Remember that parentheses are grouping symbols that indicate which operations should be done first.)
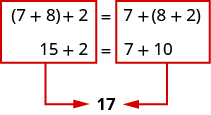
Figure \(\PageIndex{1}\)
When adding three numbers, changing the grouping of the numbers does not change the result. This is known as the Associative Property of Addition.
The same principle holds true for multiplication as well. Suppose we want to find the value of the following expression:
\[5 \cdot \dfrac{1}{3} \cdot 3\]
Changing the grouping of the numbers gives the same result, as shown in Figure \(\PageIndex{2}\).
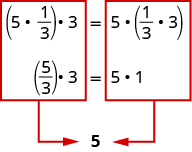
Figure \(\PageIndex{2}\)
When multiplying three numbers, changing the grouping of the numbers does not change the result. This is known as the Associative Property of Multiplication.
If we multiply three numbers, changing the grouping does not affect the product. You probably know this, but the terminology may be new to you. These examples illustrate the Associative Properties.
Definition: Associative Properties
Associative Property of Addition: if a, b, and c are real numbers, then (a + b) + c = a + (b + c)
Associative Property of Multiplication: if a, b, and c are real numbers, then (a • b) • c = a • (b • c)
Example \(\PageIndex{2}\):
Use the associative properties to rewrite the following: (a) (3 + 0.6) + 0.4 = __________ (b) \(\left(−4 \cdot \dfrac{2}{5}\right) \cdot 15\) = __________
Solution
(a) (3 + 0.6) + 0.4 = __________
| Change the grouping. | (3 + 0.6) + 0.4 = 3 + (0.6 + 0.4) |
Notice that 0.6 + 0.4 is 1, so the addition will be easier if we group as shown on the right.
(b) \(\left(−4 \cdot \dfrac{2}{5}\right) \cdot 15\) = __________
| Change the grouping. | (3 + 0.6) + 0.4 = 3 + (0.6 + 0.4) |
Notice that \(\dfrac{2}{5} \cdot 15\) is 6. The multiplication will be easier if we group as shown on the right.
Exercise \(\PageIndex{3}\):
Use the associative properties to rewrite the following: (a) (1 + 0.7) + 0.3 = __________ (b) (−9 • 8) • \(\dfrac{3}{4}\) = __________
- Answer a
-
\((1+0.7)+0.3=1+(0.7+0.3)\)
- Answer b
-
\((-9 \cdot 8) \cdot \frac{3}{4}=-9\left(8 \cdot \frac{3}{4}\right)\)
Exercise \(\PageIndex{4}\):
Use the associative properties to rewrite the following: (a) (4 + 0.6) + 0.4 = __________ (b) (−2 • 12) • \(\dfrac{5}{6}\) = __________
- Answer a
-
\((4+0.6)+0.4=4+(0.6+0.4)\)
- Answer b
-
\((-2 \cdot 12) \cdot \frac{5}{6}=-2\left(12 \cdot \frac{5}{6}\right)\)
Besides using the associative properties to make calculations easier, we will often use it to simplify expressions with variables.
Example \(\PageIndex{3}\):
Use the Associative Property of Multiplication to simplify: 6(3x).
Solution
| Change the grouping. | (6 • 3)x |
| Multiply in the parentheses. | 18x |
Notice that we can multiply 6 • 3, but we could not multiply 3 • x without having a value for x.
Exercise \(\PageIndex{5}\):
Use the Associative Property of Multiplication to simplify the given expression: 8(4x).
- Answer
-
\(32x\)
Exercise \(\PageIndex{6}\):
Use the Associative Property of Multiplication to simplify the given expression: −9(7y).
- Answer
-
\(-63y\)
Evaluate Expressions using the Commutative and Associative Properties
The commutative and associative properties can make it easier to evaluate some algebraic expressions. Since order does not matter when adding or multiplying three or more terms, we can rearrange and re-group terms to make our work easier, as the next several examples illustrate.
Example \(\PageIndex{4}\):
Evaluate each expression when x = \(\dfrac{7}{8}\). (a) x + 0.37 + (− x) (b) x + (− x) + 0.37
Solution
(a) x + 0.37 + (− x)
| Substitute \(\dfrac{7}{8}\) for x. | $$\textcolor{red}{\dfrac{7}{8}} + 0.37 + \left(- \textcolor{red}{\dfrac{7}{8}}\right)$$ |
| Convert fractions to decimals. | 0.875 + 0.37 + (-0.875) |
| Add left to right. | 1.245 - 0.875 |
| Subtract. | 0.37 |
(b) x + (− x) + 0.37
| Substitute \(\dfrac{7}{8}\) for x. | $$\textcolor{red}{\dfrac{7}{8}} + \left(- \textcolor{red}{\dfrac{7}{8}}\right) + 0.37$$ |
| Add opposites first. | 0.37 |
What was the difference between part (a) and part (b)? Only the order changed. By the Commutative Property of Addition, x + 0.37 + (− x) = x + (− x) + 0.37. But wasn’t part (b) much easier?
Exercise \(\PageIndex{7}\):
Evaluate each expression when y = \(\dfrac{3}{8}\): (a) y + 0.84 + (− y) (b) y + (− y) + 0.84.
- Answer a
-
\(0.84\)
- Answer b
-
\(0.84\)
Exercise \(\PageIndex{8}\):
Evaluate each expression when f = \(\dfrac{17}{20}\): (a) f + 0.975 + (− f) (b) f + (− f) + 0.975.
- Answer a
-
\(0.975\)
- Answer b
-
\(0.975\)
Let’s do one more, this time with multiplication.
Example \(\PageIndex{5}\):
Evaluate each expression when n = 17. (a) \(\dfrac{4}{3} \left(\dfrac{3}{4} n\right)\) (b) \(\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) n\)
Solution
(a) \(\dfrac{4}{3} \left(\dfrac{3}{4} n\right)\)
| Substitute 17 for n. | $$\dfrac{4}{3} \left(\dfrac{3}{4} \cdot \textcolor{red}{17} \right)$$ |
| Multiply in the parentheses first. | $$\dfrac{4}{3} \left(\dfrac{51}{4}\right)$$ |
| Multiply again. | $$17$$ |
(b) \(\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) n\)
| Substitute 17 for n. | $$\left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) \textcolor{red}{\cdot 17}$$ |
| Multiply. The product of reciprocals is 1. | $$(1) \cdot 17$$ |
| Multiply again. | $$17$$ |
What was the difference between part (a) and part (b) here? Only the grouping changed. By the Associative Property of Multiplication, \(\dfrac{4}{3} \left(\dfrac{3}{4} n\right) = \left(\dfrac{4}{3} \cdot \dfrac{3}{4}\right) n\). By carefully choosing how to group the factors, we can make the work easier.
Exercise \(\PageIndex{9}\):
Evaluate each expression when p = 24. (a) \(\dfrac{5}{9} \left(\dfrac{9}{5} p\right)\) (b) \(\left(\dfrac{5}{9} \cdot \dfrac{9}{5}\right) p\)
- Answer a
-
\(24\)
- Answer b
-
\(24\)
Exercise \(\PageIndex{10}\):
Evaluate each expression when q = 15. (a) \(\dfrac{7}{11} \left(\dfrac{11}{7} q\right)\) (b) \(\left(\dfrac{7}{11} \cdot \dfrac{11}{7}\right) q\)
- Answer a
-
\(15\)
- Answer b
-
\(15\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


