Translate an Equation and Solve
In previous chapters, we translated word sentences into equations. The first step is to look for the word (or words) that translate(s) to the equal sign. Table \(\PageIndex{1}\) reminds us of some of the words that translate to the equal sign.
Table \(\PageIndex{1}\)
| Equals (=) |
| is |
is equal to |
is the same as |
the result is |
gives |
was |
will be |
Let’s review the steps we used to translate a sentence into an equation.
HOW TO: TRANSLATE A WORD SENTENCE TO AN ALGEBRAIC EQUATION
Step 1. Locate the "equals" word(s). Translate to an equal sign.
Step 2. Translate the words to the left of the "equals" word(s) into an algebraic expression.
Step 3. Translate the words to the right of the "equals" word(s) into an algebraic expression.
Now we are ready to try an example.
Example \(\PageIndex{9}\):
Translate and solve: five more than x is equal to 26.
Solution
| Translate. |
 |
| Subtract 5 from both sides. |
$$x + 5 \textcolor{red}{-5} = 26 \textcolor{red}{-5}$$ |
| Simplify. |
$$x = 21$$ |
| Check: Is 26 five more than 21? |
$$\begin{split} 21 + 5 &\stackrel{?}{=} 26 \\ 26 &= 26\; \checkmark \end{split}$$ |
The solution checks.
Exercise \(\PageIndex{17}\):
Translate and solve: Eleven more than x is equal to 41.
- Answer
-
x + 11 = 41; x = 30
Exercise \(\PageIndex{18}\):
Translate and solve: Twelve less than y is equal to 51.
- Answer
-
y - 12 = 51; y = 63
Example \(\PageIndex{10}\):
Translate and solve: The difference of 5p and 4p is 23.
Solution
| Translate. |
 |
| Simplify. |
p = 23 |
| Check. |
$$\begin{split} 5p - 4p &= 23 \\ 5(23) - 4(23) &\stackrel{?}{=} 23 \\ 115 - 22 &\stackrel{?}{=} 23 \\ 23 &= 23\; \checkmark \end{split}$$ |
The solution checks.
Exercise \(\PageIndex{19}\):
Translate and solve: The difference of 4x and 3x is 14.
- Answer
-
4x - 3x = 14; x = 14
Exercise \(\PageIndex{20}\):
Translate and solve: The difference of 7a and 6a is −8.
- Answer
-
7a - 6a = -8; a = -8
Translate and Solve Applications
In most of the application problems we solved earlier, we were able to find the quantity we were looking for by simplifying an algebraic expression. Now we will be using equations to solve application problems. We’ll start by restating the problem in just one sentence, assign a variable, and then translate the sentence into an equation to solve. When assigning a variable, choose a letter that reminds you of what you are looking for.
Example \(\PageIndex{11}\):
The Robles family has two dogs, Buster and Chandler. Together, they weigh 71 pounds. Chandler weighs 28 pounds. How much does Buster weigh?
Solution
| Read the problem carefully. |
|
| Identify what you are asked to find, and choose a variable to represent it. |
How much does Buster weigh? Let b = Buster's weight. |
| Write a sentence that gives the information to find it. |
Buster's weight plus Chandler's weight equals 71 pounds. |
| We will restate the problem, and then include the given information. |
Buster's weight plus 28 equals 71. |
| Translate the sentence into an equation, using the variable b. |
$$b + 28 = 71$$ |
| Solve the equation using good algebraic techniques. |
$$\begin{split} b + 28 - 28 &= 71 - 28 \\ b &= 43 \end{split}$$ |
| Check the answer in the problem and make sure it makes sense. |
|
| Is 43 pounds a reasonable weight for a dog? Yes. Does Buster's weight plus Chandler's weight equal 71 pounds? |
$$\begin{split} 43 + 28 &\stackrel{?}{=} 71 \\ 71 &= 71\; \checkmark \end{split}$$ |
| Write a complete sentence that answers the question, "How much does Buster weigh?" |
Buster weighs 43 pounds |
Exercise \(\PageIndex{21}\):
Translate into an algebraic equation and solve: The Pappas family has two cats, Zeus and Athena. Together, they weigh 13 pounds. Zeus weighs 6 pounds. How much does Athena weigh?
- Answer
-
a + 6 = 13; Athena weighs 7 pounds
Exercise \(\PageIndex{22}\):
Translate into an algebraic equation and solve: Sam and Henry are roommates. Together, they have 68 books. Sam has 26 books. How many books does Henry have?
- Answer
-
26 + h = 68; Henry has 42 books.
HOW TO: DEVISE A PROBLEM-SOLVING STRATEGY
Step 1. Read the problem. Make sure you understand all the words and ideas.
Step 2. Identify what you are looking for.
Step 3. Name what you are looking for. Choose a variable to represent that quantity
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.
Example \(\PageIndex{12}\):
Shayla paid $24,575 for her new car. This was $875 less than the sticker price. What was the sticker price of the car?
Solution
| What are you asked to find? |
"What was the sticker price of the car?" |
| Assign a variable. |
Let s = the sticker price of the car. |
| Write a sentence that gives the information to find it. |
$24,575 is $875 less than the sticker price
$24,575 is $875 less than s
|
| Translate into an equation. |
$$24,575 = s - 875$$ |
| Solve. |
$$\begin{split} 24,575 + 876 &= s - 875 + 875 \\ 24,575 &= s \end{split}$$ |
| Check: Is $875 less than $25,450 equal to $24,575? |
$$\begin{split} 25,450 - 875 &\stackrel{?}{=} 24,575 \\ 24,575 &= 24,575\; \checkmark \end{split}$$ |
| Write a sentence that answers the question. |
The sticker price was $25,450. |
Exercise \(\PageIndex{23}\):
Translate into an algebraic equation and solve: Eddie paid $19,875 for his new car. This was $1,025 less than the sticker price. What was the sticker price of the car?
- Answer
-
19,875 = s − 1025; the sticker price is $20,900.
Exercise \(\PageIndex{24}\):
Translate into an algebraic equation and solve: The admission price for the movies during the day is $7.75. This is $3.25 less than the price at night. How much does the movie cost at night?
- Answer
-
7.75 = n − 3.25; the price at night is $11.00.
ACCESS ADDITIONAL ONLINE RESOURCES
Solving One Step Equations By Addition and Subtraction
Solve One Step Equations By Add and Subtract Whole Numbers (Variable on Left)
Solve One Step Equations By Add and Subtract Whole Numbers (Variable on Right)
Practice Makes Perfect
Solve Equations Using the Subtraction and Addition Properties of Equality
In the following exercises, determine whether the given value is a solution to the equation.
- Is y = \(\dfrac{1}{3}\) a solution of 4y + 2 = 10y?
- Is x = \(\dfrac{3}{4}\) a solution of 5x + 3 = 9x ?
- Is u = \(− \dfrac{1}{2}\) a solution of 8u − 1 = 6u?
- Is v = \(− \dfrac{1}{3}\) a solution of 9v − 2 = 3v?
In the following exercises, solve each equation.
- x + 7 = 12
- y + 5 = −6
- b + \(\dfrac{1}{4}\) = \(\dfrac{3}{4}\)
- a + \(\dfrac{2}{5}\) = \(\dfrac{4}{5}\)
- p + 2.4 = −9.3
- m + 7.9 = 11.6
- a − 3 = 7
- m − 8 = −20
- x − \(\dfrac{1}{3}\) = 2
- x − \(\dfrac{1}{5}\) = 4
- y − 3.8 = 10
- y − 7.2 = 5
- x − 15 = −42
- z + 5.2 = −8.5
- q + \(\dfrac{3}{4}\) = \(\dfrac{1}{2}\)
- p − \(\dfrac{2}{5}\) = \(\dfrac{2}{3}\)
- y − \(\dfrac{3}{4}\) = \(\dfrac{3}{5}\)
Solve Equations that Need to be Simplified
In the following exercises, solve each equation.
- c + 3 − 10 = 18
- m + 6 − 8 = 15
- 9x + 5 − 8x + 14 = 20
- 6x + 8 − 5x + 16 = 32
- −6x − 11 + 7x − 5 = −16
- −8n − 17 + 9n − 4 = −41
- 3(y − 5) − 2y = −7
- 4(y − 2) − 3y = −6
- 8(u + 1.5) − 7u = 4.9
- 5(w + 2.2) − 4w = 9.3
- −5(y − 2) + 6y = −7 + 4
- −8(x − 1) + 9x = −3 + 9
- 3(5n − 1) − 14n + 9 = 1 − 2
- 2(8m + 3) − 15m − 4 = 3 − 5
- −(j + 2) + 2j − 1 = 5
- −(k + 7) + 2k + 8 = 7
- 6a − 5(a − 2) + 9 = −11
- 8c − 7(c − 3) + 4 = −16
- 8(4x + 5) − 5(6x) − x = 53
- 6(9y − 1) − 10(5y) − 3y = 22
Translate to an Equation and Solve
In the following exercises, translate to an equation and then solve.
- Five more than x is equal to 21.
- The sum of x and −5 is 33.
- Ten less than m is −14.
- Three less than y is −19.
- The sum of y and −3 is 40.
- Eight more than p is equal to 52.
- The difference of 9x and 8x is 17.
- The difference of 5c and 4c is 60.
- The difference of n and \(\dfrac{1}{6}\) is \(\dfrac{1}{2}\).
- The difference of f and \(\dfrac{1}{3}\) is \(\dfrac{1}{12}\).
- The sum of −4n and 5n is −32.
- The sum of −9m and 10m is −25.
Translate and Solve Applications
In the following exercises, translate into an equation and solve.
- Pilar drove from home to school and then to her aunt’s house, a total of 18 miles. The distance from Pilar’s house to school is 7 miles. What is the distance from school to her aunt’s house?
- Jeff read a total of 54 pages in his English and Psychology textbooks. He read 41 pages in his English textbook. How many pages did he read in his Psychology textbook?
- Pablo’s father is 3 years older than his mother. Pablo’s mother is 42 years old. How old is his father?
- Eva’s daughter is 5 years younger than her son. Eva’s son is 12 years old. How old is her daughter?
- Allie weighs 8 pounds less than her twin sister Lorrie. Allie weighs 124 pounds. How much does Lorrie weigh?
- For a family birthday dinner, Celeste bought a turkey that weighed 5 pounds less than the one she bought for Thanksgiving. The birthday dinner turkey weighed 16 pounds. How much did the Thanksgiving turkey weigh?
- The nurse reported that Tricia’s daughter had gained 4.2 pounds since her last checkup and now weighs 31.6 pounds. How much did Tricia’s daughter weigh at her last checkup?
- Connor’s temperature was 0.7 degrees higher this morning than it had been last night. His temperature this morning was 101.2 degrees. What was his temperature last night?
- Melissa’s math book cost $22.85 less than her art book cost. Her math book cost $93.75. How much did her art book cost?
- Ron’s paycheck this week was $17.43 less than his paycheck last week. His paycheck this week was $103.76. How much was Ron’s paycheck last week?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
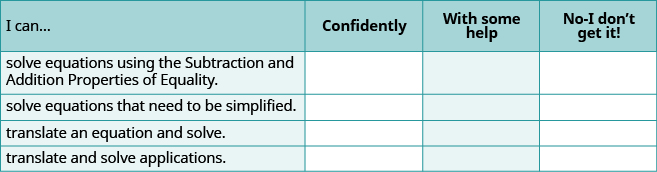
(b) If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.





