4.3: Addition Algorithms
- Last updated
- Save as PDF
- Page ID
- 82997
You will need:A Calculator, Base Blocks (Material Cards 4-15)
There is no one algorithm that everyone uses for adding numbers together. A teacher should be familiar with several methods so that the most number of students can be reached. What's important is that students understand what addition means and knows how to add numbers together one way or another. If a student figures out an algorithm that works on their own, I think that's terrific. It shows creativity and the student probably won't forget it. My hope is that more and more teachers realize many paths may lead to solving a problem correctly and that there is usually no reason to insist students work a problem in a particular way. There are many ways to solve a problem and diversity should be encouraged. This course is a little different because you are presumably interested in becoming a teacher. Therefore, it is important for you to learn as many ways as possible to work problems as well as discover some methods of your own. In this section, you will be learning a variety of algorithms for adding and should be able to work through and explain the procedures for working a problem using any of the methods presented. You will learn some new methods for addition and will be using them to add numbers in Base Ten as well as in other bases.
The DOT METHOD for adding columns of single digits
Here is a method for adding several digits together without having to keep a large running total in your head. The idea is that you only add two single digits together at a time. Any time you add and get a number over 9, you put down a dot and only keep the unit's digit in your memory. The dot stands for the ten. For instance, since 6 + 7 = 13 (which is 10 + 3), you write a dot and think 3. Think 6 + 7 = Dot 3. In the example below, to add eight numbers together, a common approach would be to add the first two digits together, then keep adding on the next digit until all eight digits have been added. In other words, someone might think: 6 + 7 is 13, 13 + 8 is 21, 21 + 3 is 24, 24 + 5 is 29, 29 + 9 is 38, 38 + 4 is 42 and 42 + 7 is 49. Although this yields the correct answer, it's easy to lose track along the way. With the DOT METHOD shown, a dot is placed by a number if after it is added on, the sum is ten or more. At each step of the way, I've written in parentheses what number you think of after adding each digit. To start, see the eight digits to be added. Step 1: 6 + 7 = 13 so write a dot and think 3; Step 2: 3 + 8 = 11 so write a dot and think 1; Step 3: 1 + 3 = 4 so think 4; Step 4: 4 + 5 =9 so think 9; Step 5: 9 + 9 = 18 so write a dot and think 8; Step 6: 8 + 4 = 12 so write a dot and think 2; Step 7: 2 + 7 = 9 so write a 9 under the bar since all digits have been added. Count the dots (4), which stands for how many tens (40) and write in front of the 9. The answer is 49. Try it on your own now!
| Start \[ \begin{aligned} 6 \\ 7\\ 8 \\ 3 \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Step 1 \[ \begin{aligned} 6 \\ 7 &\cdot (3)\\ 8 \\ 3 \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Step 2 \[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot (1)\\ 3 \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Step 3 \[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 &\ (4) \\ 5\\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Step 4 \[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5 &\ (9) \\ 9 \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Step 5 \[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot (8) \\ 4 \\ \underline{+ 7} \end{aligned} \nonumber \] | Step 6 \[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot \\ 4 &\cdot (2)\\ \underline{+ 7} \end{aligned} \nonumber \] | Step 7 \[ \begin{aligned} 6 \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot \\ 4 &\cdot\\ + 7 &\ (9) \\ \hline 49 \end{aligned} \nonumber \] |
| \[ \begin{aligned} \\ 7 &\cdot\\ 8 &\cdot\\ 3 \\ 5\\ 9 &\cdot \\ 4 &\cdot\\ \underline{+ 7 } \\ 49 \end{aligned} \nonumber \] |
In the example just shown on the previous page, every single step, including what you think is shown. In reality, this is a quick algorithm and if you looked at the problem after someone did it, the work on the left is all you would see. To the right are are two more examples. Actually, each is the same sum of numbers written in a different order, which is another way to check addition! A quick check when adding only two numbers is to reverse the order and add again.
| \[ \begin{aligned} 3 \\ 9 &\cdot\\ 6 \\ 5 &\cdot\\ 4 \\ 7 &\cdot \\ 7 &\cdot\\ \underline{+ 8 } \\ 49 \end{aligned} \nonumber \] | \[ \begin{aligned} 6 \\ 3\\ 7 &\cdot\\ 9 &\cdot\\ 7 &\cdot \\ 5 \\ 8 &\cdot\\ \underline{+ 4 } \\ 49 \end{aligned} \nonumber \] |
Exercise 1
Use the dot method to add the following columns of digits shown to the right.
| \[ \begin{aligned} 3 \\ 9 \\4 \\5\\2\\6\\8\\6\\ \underline{+ 7} \end{aligned} \nonumber \] | \[ \begin{aligned} 6 \\ 7 \\ 9\\3\\5\\8\\2\\2\\ \underline{+ 9} \end{aligned} \nonumber \] | \[ \begin{aligned} 2\\9\\6\\4\\2\\5\\7\\9\\ \underline{+ 3} \end{aligned} \nonumber \] | \[ \begin{aligned} 5\\8\\7\\6\\3\\9\\2\\5\\ \underline{+ 7} \end{aligned} \nonumber \] |
By the way, you could put the dots to the left or right of the digit, do whatever is most comfortable for you. If you are adding without paper and pencil, use your fingers to keep track of the dots! Instead of writing a dot, put up a finger. The beauty of this addition is you never have to keep a number higher than nine in your head!
Exercise 2
The dot method could also be used to add several digits written in a horizontal format. The dots could be placed over the numerals. Try it on the following problems. Make up your own problems for part d and part e.
| a. 7 + 6 + 4 + 5 + 9 + 6 + 8 + 3 + 4 + 9 + 8 = ____ |
| b. 4 + 9 + 6 + 2 + 9 + 7 + 7 + 6 + 8 + 4 + 8 = ____ |
| c. 7 + 9 + 8 + 5 + 9 + 4 + 2 + 6 + 9 + 8 + 7 = ____ |
| d. |
| e. |
The Scratch Method
The Scratch Method is similar to the dot method. Any time you add and get a number over nine, you scratch off the last digit added. The scratch, like the dot, will represent ten. Just as in the dot method, you only keep the unit's digit in your memory or as an alternative, write the unit's digit to the right and just below the digit just scratched off. This can be done in the dot method also. I'll illustrate the steps involved by writing down the unit's digits this time. When the sum is less than ten, it is kept in your head. Parentheses will be used to denote what I am thinking in my head. The following problem is exactly the same one I did before when using the dot method. To start, see the eight digits to be added. Step 1: 6 + 7 = 13 so scratch off the 7 and write 3; Step 2: 3 + 8 = 11 so scratch off the 8 and write 1; Step 3: 1 + 3 = 4 so think 4; Step 4: 4 + 5 =9 so think 9; Step 5: 9 + 9 = 18 so scratch off the 9 and write 8; Step 6: 8 + 4 = 12 so scratch off the 4 and write 2; Step 7: 2 + 7 = 9 so write a 9 under the bar since all digits have been added. Count the scratches (4), which stands for how many tens (40) and write in front of the 9. The answer is 49. Try the problem on your own.
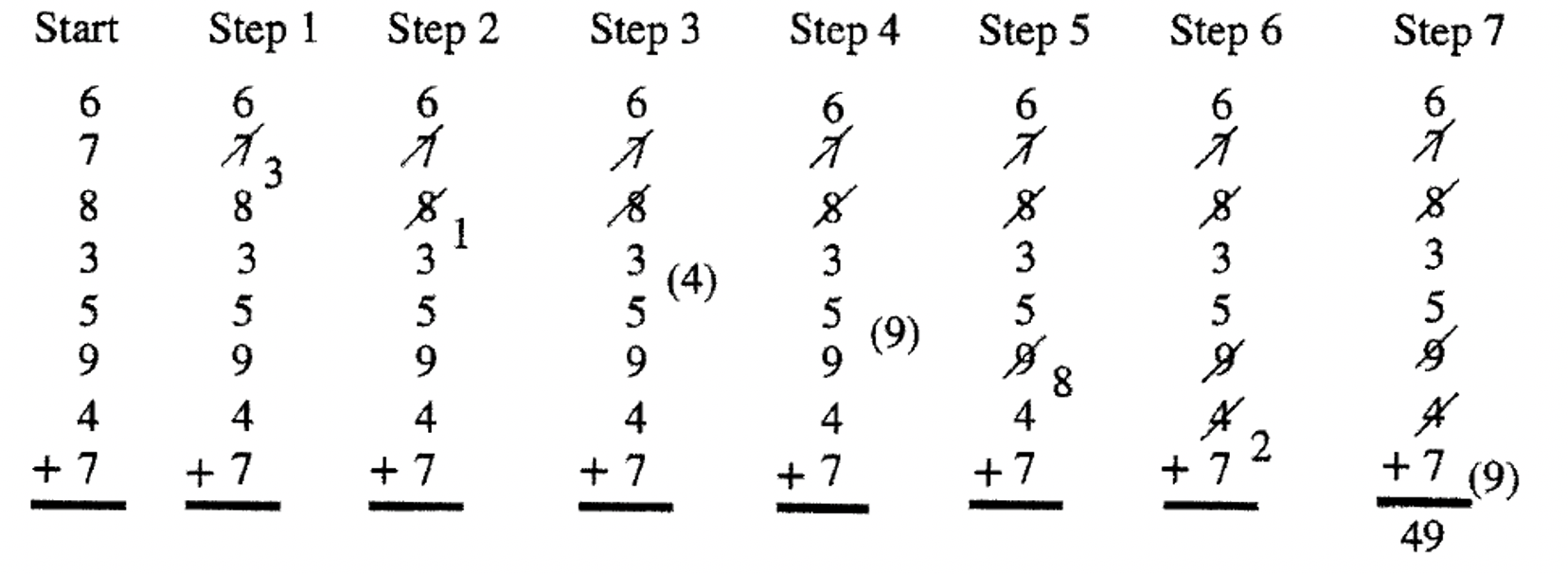
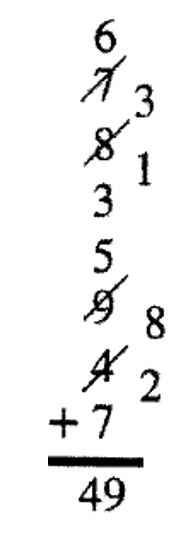
The above problem shows every single step, including what you think as you go along. If you were to look at the problem after someone did it, it would look like what you see on the left. More examples are shown on the right. Keeping the unit's digit in memory is faster than writing them down at each step. Try it both ways and ten adopt what's easiest and/or faster for you.
Exercise 3
Use the scratch method to add the following columns of digits. Make up your own problem with at least 12 numbers for part e.
| a. \( \begin{aligned} 3 \\ 9 \\3 \\6\\5\\8\\6\\ \underline{+ 7} \end{aligned}\) | b. \( \begin{aligned} 5 \\ 3 \\ 9\\6\\7\\4\\2\\ \underline{+ 7} \end{aligned}\) | c. \( \begin{aligned} 8\\8\\5\\7\\9\\7\\6\\ \underline{+ 3} \end{aligned}\) | d. \( \begin{aligned} 7\\6\\4\\3\\8\\9\\7\\ \underline{+ 9} \end{aligned}\) | e. |
The Dot and Scratch Methods can be used to add numerals with more than one digit. Add one column at a time, leaving a little space between the columns for dots if you use the Dot Method. To the right is an example of adding using the Scratch method with the usual method of adding from right to left and carrying. In this case, I am keeping each unit's digit in my head as opposed to writing each digit down after each scratch. The first column has four scratches, so the 4 is carried to column 2. NOTE: Unless you practice several problems using these methods, it probably won't seem easier to add using one of these ways than whatever method you are used to using. But if you practice, you will probably become a whiz at addition and never go back to the old way!
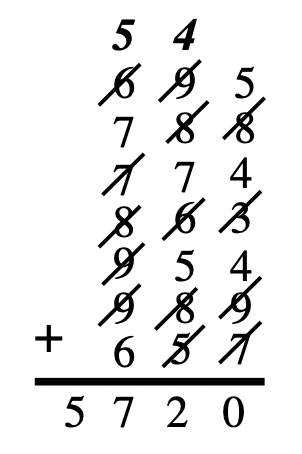
The most common addition algorithm is the Right To Left Standard Addition Algorithm, often referred to as the Standard Addition Algorithm. This is the one almost everyone grew up learning. You start on the right and add the digits. The unit's digit is put down under the line and the ten's digit is carried to the top of the next column to the left. Get out your Base Ten Blocks now to understand what is really going on.
Consider the addition problem 246 + 178. From our knowledge of place value, we know that 246 is 2100 + 4
10 + 6 (or 200 + 40 + 6) and 178 is 1
100 + 7
10 + 8 (or 100 + 70 + 8). Using Base Ten blocks, 246 would be represented with 2 flats, 4 longs and 6 units whereas 178 would be represented with 1 flat, 7 longs and 8 units. So, the addition problem can be thought of in the following way:
Using Base Blocks
\[\begin{aligned} 2 \text{ flat(s) } + 4 \text{ long(s) } +6 \text{ unit(s) } \\
\underline{+ 1 \text{ flat(s) } + 7 \text{ long(s) } + 8 \text{ unit(s) }} \end{aligned} \nonumber \]
This addition problem using blocks is shown below:
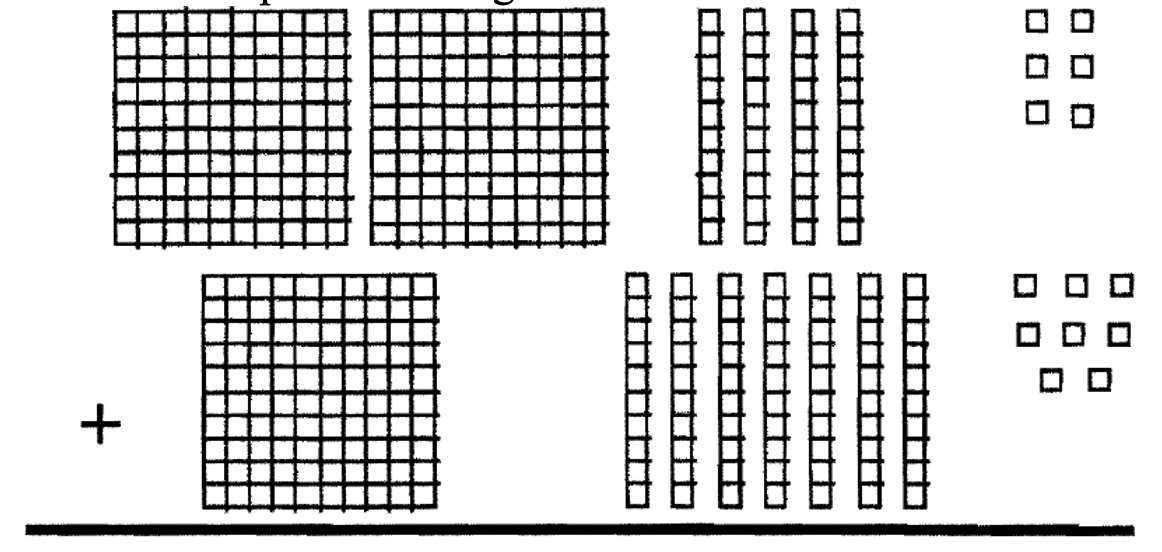
If we add, we get:
\[\begin{aligned} 2 \text{ flat(s) } + 4 \text{ long(s) } +6 \text{ unit(s) } \\
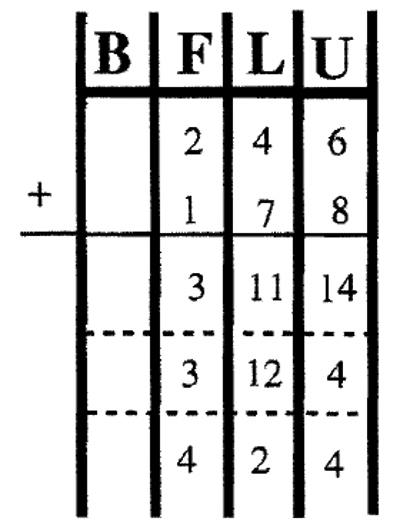
\underline{+ 1 \text{ flat(s) } + 7 \text{ long(s) } + 8 \text{ unit(s) }} \\ 3 \text{ flat(s) } +11 \text{ long(s) } +14 \text{ unit(s) } \end{aligned} \nonumber \]
Trades can now be made. Ten of the 14 units can be exchanged for a long. That leaves us with 3 flats, 12 longs and 4 units. The sum and trades are illustrated with blocks on the next page.
After trading, sum = 3 flat(s) + 12 long(s) + 4 unit(s)
After combining the blocks, the sum is shown below.
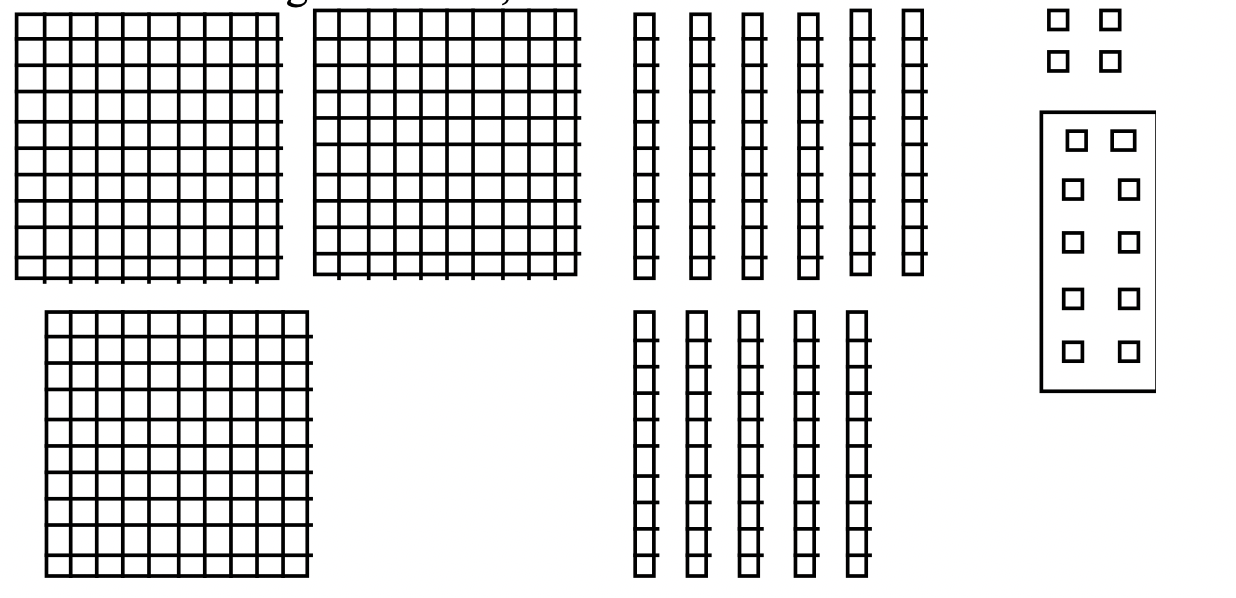
The next step is to trade in ten units for a long. I've put a box around the units to be traded above. This yields 3 flats, 12 longs and 4 units as shown below.
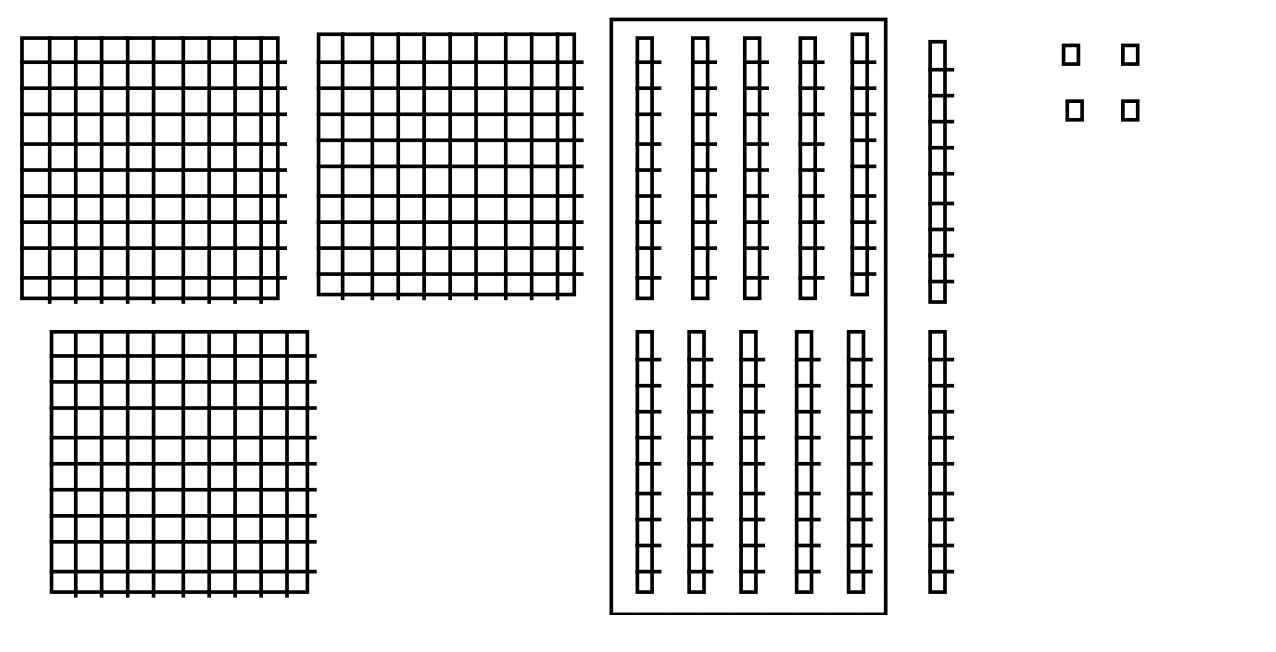
Now ten of the 12 longs can be exchanged for a flat. I've put a box around ten of the longs to be traded above. After the exchange, the sum is 4 flats, 2 longs and 4 units, which is 424. This is illustrated below.
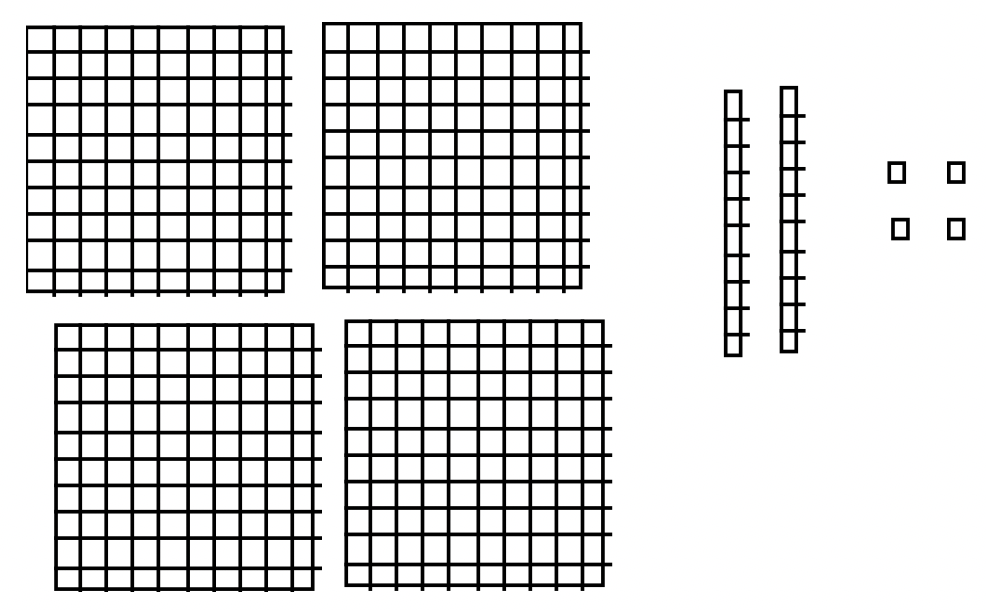
After making all traded, the final sum = 4 flat(s) + 2 long(s) + 4 unit(s)
We're in Base Ten, so the answer is 424. Therefore, 246 + 178 = 424.
In the previous example of adding 246 + 178 using the Base Blocks, ten longs could have been exchanged for a flat at the same time that ten units were exchanged for a long. I only did one trade at a time because in the Standard Addition Algorithm, we don't combine all the blocks (or place values) at once. First, the units are added together to get 14. The 4 is written down in the unit's column and the other 10 units are written as 1 long in the next column to signify that there is another long. Now, there are 1 + 4 + 7 longs to add up, which is 12. The 2 is written down in the longs column and the other 10 units are written as 1 flat in the next column to signify that there is another flat. Finally, there are 1 + 2 + 1 flats to add up, which is 4. So the sum is 4 flats, 2 longs and 4 units, which is 424. The exchanges being made is what carrying is all about. To the right is another way of keeping track of blocks, flats, longs and units. Notice the trades being made at each step. If the largest addend has x digits, I make x + 1 columns to allow for carrying. In this problem, there are three digits for each addend, so I made four columns to allow for a possible block being made.
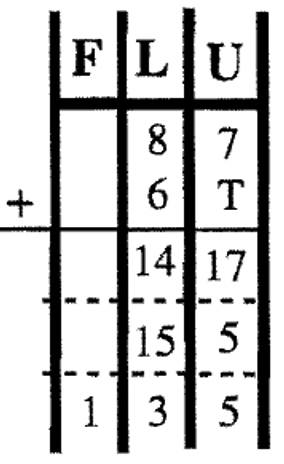
Now, let's perform this basic algorithm in other bases. If you are adding in Base Seven, the trick here is to recall basic addition facts in Base Seven. You need to know your addition tables. Remember \(5_{\text{seven}} + 6_{\text{seven}} = 11_{\text{ten}}\), which is \(14_{\text{seven}}\) (which is one long and four units in Base Seven). Study the examples below. To help visualize the trades, the problems are first done using a chart with the sums written in Base Ten to keep track of the units, longs, flats, etc. In exchanging blocks, the conversion to the proper unit is accomplished. Then, the same problems are done without using the charts and using the traditional carrying method –here, you add in the base given as you go along. Try these five problems on your own before going on to the next exercise.
| \(\begin{aligned} 45_{\text{seven}} \\ \underline{+36_{\text{seven}}} \end{aligned} \) | \(\begin{aligned} 63_{\text{eight}} \\ \underline{+ 45_{\text{eight}}} \end{aligned} \) | \(\begin{aligned} 23_{\text{four}} \\ \underline{+ 12_{\text{four}}} \end{aligned} \) | \(\begin{aligned}87_{\text{twelve}} \\ \underline{+ 6T_{\text{twelve}}} \end{aligned} \) | \(\begin{aligned} 101_{\text{two}} \\ \underline{+ 111_{\text{two}}} \end{aligned}\) |
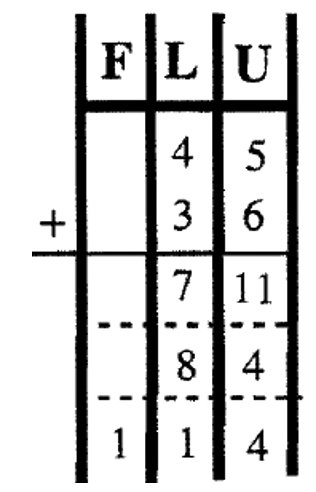 |
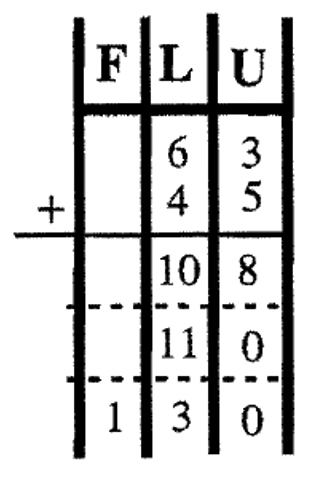 |
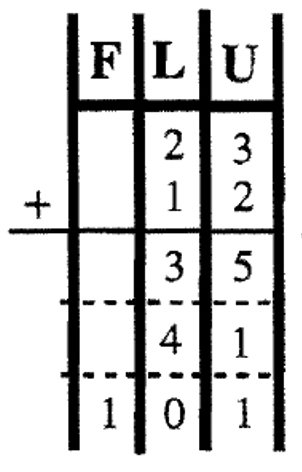 |
 |
 |
The same examples are worked below using the traditional carrying algorithm.
| \(\begin{aligned} ^{1} \\& 45_{\text{seven}} \\& \underline{+36_{\text{seven}}} \\ & 114_{\text{seven}}\end{aligned} \) | \(\begin{aligned} ^{1} && ^{1} \\&63_{\text{eight}} \\ &\underline{+ 45_{\text{eight}}} \\& 130_{\text{eight}} \end{aligned} \) | \(\begin{aligned} &^{1}\\ 23_{\text{four}} \\ \underline{+ 12_{\text{four}}}\\ 101_{\text{four}} \end{aligned} \) |
\(\begin{aligned} &^{11}\\ 87_{\text{twelve}} \\ \underline{+ 6T_{\text{twelve}}} \\ 135_{\text{twelve}} \end{aligned}\) |
\(\begin{aligned} 101_{\text{two}} \\ \underline{+ 111_{\text{two}}} \\ 1100_{\text{two}} \end{aligned}\) |
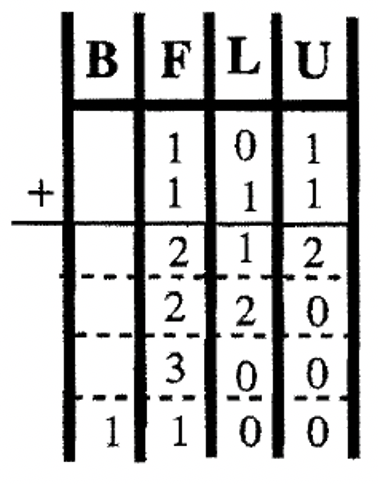
Exercise 4
Add the following. Do each problem using charts as shown in the previous examples. Use your Base Blocks to visualize the problem further.
| a. \(\begin{aligned} &7 & E && 1 & \ {}_{\text{thirteen}} \\ + & 5 &8 &&4& \ {}_{\text{thirteen}} \end{aligned}\) | b. \(\begin{aligned} &1 & 1 && 0 && 1 \ {}_{\text{two}} \\ +& 1 & 0 && 0 && 1 \ {}_{\text{two}} \end{aligned}\) | c. \(\begin{aligned} &3 & 2 && 0 && 4 \ {}_{\text{five}} \\ +& 4 & 0 && 1 && 3 \ {}_{\text{five}} \end{aligned}\) | d. \(\begin{aligned} &6 & 1 && 2 & \ {}_{\text{nine}} \\ + & 4 &5 &&6& \ {}_{\text{nine}} \end{aligned}\) |
 |
 |
 |
 |
| e. \(\begin{aligned} &1 &&0 & 1 && 1 && 1 \ {}_{\text{two}} \\ +&1&& 1 & 1 && 0 && 1 \ {}_{\text{two}} \end{aligned}\) | f. \(\begin{aligned} 2&&2 && 1 && 2 & \ {}_{\text{three}} \\ + && 2 &&2 && 2 & \ {}_{\text{three}} \end{aligned}\) | g. \(\begin{aligned} &4 & 6 && 1 && 3 \ {}_{\text{twelve}} \\ +& 5 & T && 3 && 9 \ {}_{\text{twelve}} \end{aligned}\) | h. \(\begin{aligned} &4 & 3 && 4 && 3 \ {}_{\text{seven}} \\ +& 4 & 1 && 4 && 5 \ {}_{\text{seven}} \end{aligned}\) |
 |
 |
 |
 |
Exercise 5
Eventually, you should be able to do the above problems without the use of charts or manipulatives. You can always think in terms of blocks as you work them. Add the following using the traditional carrying algorithm. Practice until you feel confident and are proficient at adding without using charts or manipulatives.
| a. \(\begin{aligned} &7 & E && 1 & \ {}_{\text{thirteen}} \\ + & 5 &8 &&4& \ {}_{\text{thirteen}} \end{aligned}\) | b. \(\begin{aligned} &1 & 1 && 0 && 1 \ {}_{\text{two}} \\ +& 1 & 0 && 0 && 1 \ {}_{\text{two}}\\ \hline \end{aligned}\) | c. \(\begin{aligned} &3 & 2 && 0 && 4 \ {}_{\text{five}} \\ +& 4 & 0 && 1 && 3 \ {}_{\text{five}}\\ \hline \end{aligned}\) | d. \(\begin{aligned} &6 & 1 && 2 & \ {}_{\text{nine}} \\ + & 4 &5 &&6& \ {}_{\text{nine}} \end{aligned}\) |
| e. \(\begin{aligned} &1 &&0 & 1 && 1 && 1 \ {}_{\text{two}} \\ +&1&& 1 & 1 && 0 && 1 \ {}_{\text{two}} \end{aligned}\) | f. \(\begin{aligned} 2&&2 && 1 && 2 & \ {}_{\text{three}} \\ + && 2 &&2 && 2 & \ {}_{\text{three}}\\ \hline \end{aligned}\) | g. \(\begin{aligned} &4 & 6 && 1 && 3 \ {}_{\text{twelve}} \\ +& 5 & T && 3 && 9 \ {}_{\text{twelve}} \\ \hline \end{aligned}\) | h. \(\begin{aligned} &4 & 3 && 4 && 3 \ {}_{\text{seven}} \\ +& 4 & 1 && 4 && 5 \ {}_{\text{seven}} \\ \hline \end{aligned}\) |
Another way to add is by using expanded notation. Our first example, 246 + 178, can be written as (200 + 40 + 6) + (100 + 70 + 8). Using the commutative and associative properties, this sum can be written as (200 + 100) + (40 + 70) + (6 + 8) or 300 + 110 + 14 = 300 + (100 + 10) + (10 + 4) = (300 + 100) + (10 + 10) + 4 = 400 + 20 + 4 = 424. When written out like this, it is perhaps more clear what is really being added as opposed to doing it by rote without thinking about the place value of each digit.
Exercise 6
6. Add by using expanded notation. Show all steps.
a. 43 + 47
b. 88 + 54
Exercise 7
7. Suppose two different students add two numbers together as shown in the two problems to the right. Both have very similar methods. Explain what each student is doing and why it makes sense. Then, make up two more problems and add using one of these methods.
| \(\begin{aligned}859 \\ \underline{+ 467} \\ 16 \\ 110 \\ \underline{+ 1200} \\ 1326 \end{aligned}\) | \(\begin{aligned}859 \\ \underline{+ 467} \\ 1200 \\ 110 \\ \underline{+ 16} \\ 1326 \end{aligned}\) |
Below is the work of three different students doing the same addition problem. Figure out what each student is doing to get the answer before reading on.
| \(\begin{aligned}859 \\ \underline{+ 467} \\ 1200 \\ 1310 \\ 1326 \end{aligned}\) | \(\begin{aligned}859 \\ \underline{+ 467} \\ 1259 \\ 1319 \\ 1326 \end{aligned}\) | \(\begin{aligned}859 \\ \underline{+ 467} \\ 866 \\ 926 \\ 1326 \end{aligned}\) |
The first student starts by adding the hundreds together (800 + 400 = 1200). Next, the tens are added together (50 + 60 = 110) and that answer is added on (1200 + 110 = 1310). Finally, the ones are added (9 + 7 = 16) and that is added on to get the answer (1310 + 16 = 1326). The second student takes the first number and adds on the hundreds of the second number (859 + 400 = 1259). Next, the tens of the second number is added on (1259 + 60 = 1319). Finally, the ones are added on (1319 + 7 = 1326). The third student starts with the first number and adds on the ones of the second digit first (859 + 7 = 866). Second, the tens digit of the second number is added on (866 + 60 = 926). Finally, the hundreds is added on (926 + 400 = 1326). Someone might be more inclined to use one of these methods if they are adding in their head.
Exercise 8
Make up your own problem and solve using the three methods explained above. Explain the method and steps used to arrive at the correct answer.
Another method used for adding is the Left to Right Addition Algorithm. Some of the last few examples were actually employing Left to Right algorithms. In expanded notation, you could add left to right or right to left. Many people find the Left to Right Addition Algorithm easier because there is no carrying. There are a couple of ways to perform this method. Start by adding the leftmost column of digits first. As you move to the next column to the right, you add the digits. If the sum is more than 9, write the unit's digit under that column and underline the digit already put down immediately to the left. This is similar to carrying but you don't need to move up to the next column –it gets added on to the answer later. Continue until you've added the unit's digits. Then go back and add one to all the digits that are underlined. Can you understand why? The following example takes you step by step using this algorithm.
| Step 1: Starting in the leftmost column, add the digits (3 and 4). Since 3 + 4 = 7, write 7 under that leftmost column. | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline 7 & && && \end{aligned}\) |
| Step 2: Add the digits in the next column to the right. Since 6 + 8 = 14, write the 4 under that column and underline the digit to the left (\(\underline{7}\)). | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && && \end{aligned}\) |
| Step 3: Add the digits in the next column to the right. Since 3 + 2 is 5, write a 5 under that column. | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && 5 && \end{aligned}\) |
| Step 4: Add the digits in the next column to the right. Since 7 + 8 = 15, write the 5 under that column and underline the digit to the left (\(\underline{5}\)). | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && \underline{5} && 5 \end{aligned}\) |
| Step 5: The last step is to rewrite the answer to the problem by adding a 1 to any digit that is underlined. Thus the answer is 8465. | \(\begin{aligned} &4 & 6 && 3 && 7 \\ +& 3 & 8 && 2 && 8 \\ \hline \underline{7} && 4 && \underline{5} && 5 \\ 8 && 4 && 6 && 5 \end{aligned}\) |
Note: Step 5 is what the problem looks like when it's done, as shown in the examples below. Study and then try the following examples on your own before going on to the next exercise.
| \(\begin{aligned} 6483 \\ +5734 \\ \hline 1\underline{1} \underline{1} 1 7 \\ 12217 \end{aligned}\) | \(\begin{aligned} 5417 \\ +3971 \\ \hline \underline{8} 388 \\ 9388 \end{aligned}\) | \(\begin{aligned} 63925 \\ +41738 \\ \hline 10\underline{4}6 \underline{5} 3 \\ 105663 \end{aligned}\) | \(\begin{aligned} 787878 \\ +65656 \\ \hline \underline{7}\underline{4}\underline{2}\underline{4} \underline{2}4 \\ 853534 \end{aligned}\) |
Exercise 9
| a. \(\begin{aligned} 5386 \\ \underline{+ 6723}\end{aligned}\) | b. \(\begin{aligned} 65381 \\\underline{+ 46082}\end{aligned}\) | c. \(\begin{aligned} 6789 \\ \underline{+ 9879}\end{aligned}\) | d. \(\begin{aligned} 70426 \\ \underline{+ 57908}\end{aligned}\) |
In the Left to Right Algorithm, anytime a 9 is underlined, you must continue the underline to include the digit to the left of the nine (if there is a digit to its left). If the digit to the left is a 9, continue the underline to include the digit to its left. Keep underlining until you underline a digit that is not a nine. Then, when you go back, add 1 to the underlined number, (which will now be more than one digit). Study and then practice the following four examples on your own before attempting the next exercise.
| \(\begin{aligned} 4672 \\ \underline{+ 5826} \\ \underline{9} 498 \\ \\ 10498 \end{aligned}\) | \(\begin{aligned} 8468 \\ \underline{+ 5538} \\ 1 \underline{399} 6 \\ \\ 14006 \end{aligned}\) | \(\begin{aligned} 5798 \\ \underline{+ 4605} \\ \underline{9} \underline{39}3 \\ \\ 10403 \end{aligned}\) | \(\begin{aligned} 35776 \\ \underline{+ 64525} \\ \underline{99} \underline{29}1 \\ \\ 100301 \end{aligned}\) |
Using this technique, the first example adds 1 to 9 to get 10. In the second example, 1 is added to 399 to get 400. In the third example, 1 is added to 9 to get 10 and 1 is added to 39 to get 40. In the fourth example, 1 is added to 99 to get 100 and 1 is added to 29 to get 30.
Exercise 10
Use the Left to Right Algorithm to add the following numbers using the above technique.
| a. \(\begin{aligned} 7658 \\ \underline{+ 1147}\end{aligned}\) | b. \(\begin{aligned} 4804 \\\underline{+ 5659}\end{aligned}\) | c. \(\begin{aligned} 5679 \\ \underline{+ 7350}\end{aligned}\) | d. \(\begin{aligned} 98765 \\ \underline{+ 7238}\end{aligned}\) |
On the next page are some addition problems in other bases. The Left to Right Addition Algorithm is being used. Be careful to pay attention to the base. For example, in Base Six, any time you add and get a number higher than 5 (which is the highest digit in Base Six), you only write down the unit's digit under that column and underline the digit to its left. In Base Three, any time you add and get a number higher than 2 (which is the highest digit in Base Three), you only write down the unit's digit under that column and underline the digit to its left. In Base Twelve, any time you add and get a number higher than E (which is the highest digit in Base Twelve), you only write down the unit's digit under that column and underline the digit to its left. Make sure you understand and can do these next examples successfully on your own before going on to the next paragraph and examples.
| \(\begin{aligned} 423 \ {}_{\text{six}} \\ \underline{+503} \ {}_{\text{six}} \\ 13\underline{2}0 \ {}_{\text{six}} \\ 1330 \ {}_{\text{six}} \end{aligned}\) | \(\begin{aligned} 839 {}_{\text{twelve}} \\ \underline{+ E58} \ {}_{\text{twelve}} \\ 17\underline{8}5 \ {}_{\text{twelve}} \\ 1795 \ {}_{\text{twelve}}\end{aligned}\) | \(\begin{aligned}580 \ {}_{\text{nine}} \\ \underline{+ 723} \ {}_{\text{nine}} \\ 1\underline{3}13 \ {}_{\text{nine}} \\ 1413 \ {}_{\text{nine}}\end{aligned}\) | \(\begin{aligned}1011 \ {}_{\text{two}} \\ \underline{+ 1011} \ {}_{\text{two}} \\ 10\underline{0}\underline{0}0 \ {}_{\text{two}} \\ 10110 \ {}_{\text{two}}\end{aligned}\) | \(\begin{aligned}2012 \ {}_{\text{three}} \\ \underline{+ 1112} \ {}_{\text{three}} \\ 10\underline{1}\underline{2}1 \ {}_{\text{three}} \\ 10201 \ {}_{\text{three}}\end{aligned}\) |
Below are some examples where you have to do some continuous underlining similar to examples shown previously in Base Ten. Pay close attention to the base. If you underline a 5 in Base Six, you must continue underlining the digit to its left until you underline a digit less than 5! If you underline a 2 in Base Three, you must continue underlining the digit to its left until you underline a digit less than 2! If you underline an E in Base Twelve, you must continue underlining the digit to its left until you underline a digit less than E!. Study and practice the five examples below on your own before attempting the next exercise.
| \(\begin{aligned} 324 \ {}_{\text{six}} \\ \underline{+132} \ {}_{\text{six}} \\ \underline{45}0 \ {}_{\text{six}} \\ 500 \ {}_{\text{six}} \end{aligned}\) | \(\begin{aligned} 367 \ {}_{\text{twelve}} \\ \underline{+ 35E} \ {}_{\text{twelve}} \\ \underline{6E}6 \ {}_{\text{twelve}} \\ 706 \ {}_{\text{twelve}}\end{aligned}\) | \(\begin{aligned} 528 \ {}_{\text{nine}} \\ \underline{+367} \ {}_{\text{nine}} \\ \underline{88}6 \ {}_{\text{nine}} \\ 1006 \ {}_{\text{nine}}\end{aligned}\) | \(\begin{aligned} 1011 \ {}_{\text{two}} \\ \underline{+1110} \ {}_{\text{two}} \\ 1\underline{01}01 \ {}_{\text{two}} \\ 11001 \ {}_{\text{two}}\end{aligned}\) | \(\begin{aligned} 22021 \ {}_{\text{three}} \\ \underline{+1002} \ {}_{\text{three}} \\ \underline{2}0\underline{02}0 \ {}_{\text{three}} \\ 100100 \ {}_{\text{three}}\end{aligned}\) |
Exercise 11
Use the Left to Right Addition Algorithm to add the following. Pay careful attention to the Base!!!
| a. \(\begin{aligned} 514 \ {}_{\text{six}} \\ \underline{ + 342 \ {}_{\text{six}}} \end{aligned}\) | b. \(\begin{aligned}835 \ {}_{\text{eleven}} \\ \underline{ + 658 \ {}_{\text{eleven}}} \end{aligned}\) | c. \(\begin{aligned}473 \ {}_{\text{eight}} \\ \underline{ + 473 \ {}_{\text{eight}}} \end{aligned}\) | d. \(\begin{aligned}1111 \ {}_{\text{two}} \\ \underline{ + 1010 \ {}_{\text{two}}} \end{aligned}\) | a. \(\begin{aligned}2034 \ {}_{\text{five}} \\ \underline{ + 1112 \ {}_{\text{five}}} \end{aligned}\) |
| f. \(\begin{aligned}7E1 \ {}_{\text{thirteen}} \\ \underline{ + 584 \ {}_{\text{thirteen}}} \end{aligned}\) | f. \(\begin{aligned}1101 \ {}_{\text{two}} \\ \underline{ + 1001 \ {}_{\text{two}}} \end{aligned}\) | f. \(\begin{aligned}3204 \ {}_{\text{five}} \\ \underline{ + 4013 \ {}_{\text{five}}} \end{aligned}\) | f. \(\begin{aligned}612 \ {}_{\text{nine}} \\ \underline{ + 456 \ {}_{\text{nine}}} \end{aligned}\) |
| j. \(\begin{aligned}10111 \ {}_{\text{two}} \\ \underline{ + 11101 \ {}_{\text{two}}} \end{aligned}\) | k. \(\begin{aligned}2212 \ {}_{\text{three}} \\ \underline{ + 222_{\text{three}}} \end{aligned}\) | l. \(\begin{aligned}4613_{\text{twelve}} \\ \underline{ + 5T39_{\text{twelve}}} \end{aligned}\) | m. \(\begin{aligned}4343_{\text{seven}} \\ \underline{ + 4145_{\text{seven}}} \end{aligned}\) |
Exercise 12
List all bases between two and thirteen in which each of the following addition problems are valid.
| a. \(\begin{aligned} 403 \\ \underline{+ 542} \\ 1245 \end{aligned}\) | b. \(\begin{aligned}729\\ \underline{+ 526} \\ W52\end{aligned}\) | c. \(\begin{aligned}E83\\ \underline{+ 1T3} \\ 1166\end{aligned}\) | d. \(\begin{aligned}1011\\ \underline{+ 1111} \\ 2122\end{aligned}\) | e. \(\begin{aligned}2012\\ \underline{+ 1011} \\ 3023\end{aligned}\) |
Exercise 13
Someone started to do each of these addition problems using the Standard Right to Left Algorithm. Figure out which base each addition problem is in and finish the computation.
| a. \(\begin{aligned} 64 \\ \underline{+ 46} \\ 2 \end{aligned}\) | b. \(\begin{aligned}53\\ \underline{+ 28} \\ 2\end{aligned}\) | c. \(\begin{aligned}21\\ \underline{+ 12} \\ 0\end{aligned}\) | d. \(\begin{aligned}57\\ \underline{+ 66} \\ 3\end{aligned}\) |
Exercise 14
Someone was adding 47 + 68 in her head and said out loud, "47 + 70 = 117 and two less is 115." Explain her reasoning.
Exercise 15
Another person was adding 47 + 68 in his head and said out loud "40 + 60 is 100 and 8 + 7 is 15, so the answer is 115." Explain his reasoning.
Exercise 16
The methods in exercises 14 and 15 can be called Break-Apart Methods. You break apart one or both of the addends using the place value of the number. Mentally compute 97 + 88 and then explain the method you used.
Exercise 17
Are there any addition tricks you use? Extra credit for sharing on the Forum
Below is another addition algorithm, called the Lattice Method for Addition, used for adding two numbers together. First, add down the columns, then down the diagonals. The addition problem is 568 + 457 and the answer is 1,025. See if you can understand how to do it and understand why it works. We'll use the lattice method again when we do multiplication.
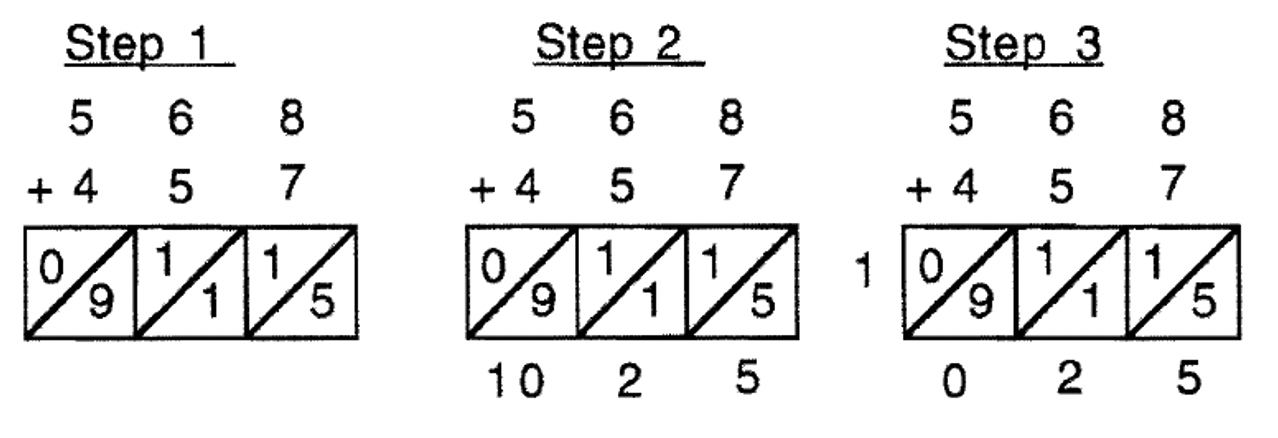
Exercise 18
Use the lattice method to compute 456 + 659. Show your work.
Exercise 19
Use the lattice method to compute the following:
| a. \(12_{\text{six}} + 25_{\text{six}}\) | b. \(T4E_{\text{thirteen}} + 190_{\text{thirteen}}\) |
Learning to estimate is a very useful skill. The idea is to convert the actual numbers in the problem to simpler numbers that are easy to compute mentally. In exercise 14, 47 + 68 is close to adding 50 + 70, which is 120. 120 is pretty close –it's within 5% of the exact answer of 115. Even if you need to know the exact answer, if you do a quick estimate, you can usually tell if you're in the ball park. Sometimes estimating is all that is really necessary. For instance, if you are shopping for groceries and have a limited amount of cash on hand to pay for them, you might want to mentally add up what you spend as you go along. The quickest way to estimate is to round. And if you want to make sure you don't go over your allotted amount, you can always just round up. Let's say you had ten items in the cart for the following amounts:
| $6.75 | $3.23 | $1.25 | $7.18 | $2.98 | $1.89 | $1.50 | $2.45 | $3.69 | $.76 |
There are many ways you could choose to round and add –you could round to the nearest dollar, or up to the nearest dollar (to make sure you don't go over) or maybe to the nearest 50 cents. I am going to assume you know how to round numbers already. And you should be able to add in your head using your fingers and the Dot Method. The following are three examples of how you might get an estimate of what the grocery bill will be.
| Rounding to the nearest dollar: 7 + 3 + 1 + 7 + 3 + 2 + 2 + 2 + 4 + 1 = 32 |
| Rounding up to the nearest dollar: 7 + 4 + 2 + 8 + 3 + 2 + 2 + 3 + 4 + 1 = 36 |
| Rounding to the nearest 50 cents: 7 + 3 + 1.5 + 7 + 3 + 2 + 1.5 + 2.5 + 3.5 + 1 = 32 |
The actual sum is $31.68 which is extremely close to our rough estimate of $32 which we got rounding both to the nearest dollar and to the nearest 50 cents. If you are working with higher priced items, you might round to the nearest ten or hundred dollars, etc.
Exercise 20
Mentally estimate the cost of the grocery bill containing the following priced items. Explain how you did it. Then, compare your answer to the actual sum.
| $4.67 | $8.21 | $9.53 | $5.33 | $2.79 | $1.89 | $2.14 | $4.65 | $5.14 | $.83 |
Exercise 21
Pretend you are going shopping and you buy ten items where each item is less than $10. List the actual cost of each item (make these up) and estimate the total. Then, compute the actual cost of the ten items.
Exercise 22
When do you think you might get too high or low of an estimate? Give an example.


