4.5: Subtraction Algorithms

You will need: Base Blocks (Material Cards 4-15)

The most common subtraction algorithm is the Right to Left Standard Subtraction Algoithm, which is where you start in the ones column and subtract, then move to the left and subtract at each column. The problem, of course, is when the top digit is less than the bottom digit and you have to regroup. Get out your Base Ten blocks now to see what is really going on.

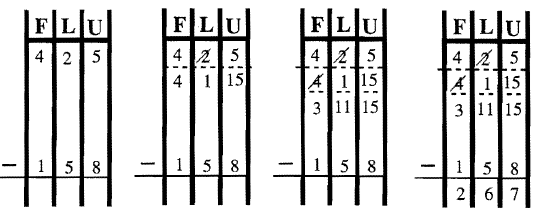
Consider the subtraction problem 425 –158. From our knowledge of place value, we know that 425 is is 4 \(\times\) 100 + 2 \(\times\) 10 + 5 (or 400 + 20 + 5) and 158 is 1 \(\times\) 100 + 5 \(\times\) 10 + 8 (or 100 + 50 + 8). Using Base Ten blocks, 425 would be represented with 4 flats, 2 longs and 5 units whereas 158 would be represented with 1 flat, 5 longs and 8 units. So, the subtraction problem can be thought of in the following way:

Using Base Blocks \[\begin{aligned} (4 \text{ flat(s) } + 2 \text{ long(s) } + 5 \text{ unit(s) }) \\ \underline{– (1 \text{ flat(s) } + 5 \text{ long(s) } + 8 \text{ unit(s) })} \end{aligned} \nonumber \]

Using blocks, the subtraction problem is shown below:

We can't subtract 8 units from 5 units, so a long is exchanged for ten units, which gives 4 flats, 1 long and 15 units in the minuend. Now, we also can't subtract 5 longs from 1 long, so 1 flat is exchanged for ten longs, which gives 3 flats, 11 longs and 15 units in the minuend. Now we can subtract at each column, which is shown on the next page. You can use either the take away approach or the missing addends approach to subtract. Use your base blocks to work through these problems.

Using Base Blocks \[\begin{aligned} &(3 \text{ flat(s) } + 11 \text{ long(s) } + 15 \text{ unit(s)}) \\ -& (1 \text{ flat(s) } + 5 \text{ long(s) } + 8 \text{ unit(s)}) \\ \hdashline &2 \text{ flat(s) } + 6 \text{ long(s) } + 7 \text{ unit(s)}) = \underline{267} \end{aligned} \nonumber \]

The subtraction problem using blocks is shown below:

Since we are working in Base Ten, the answer (difference) is 267. So, 425 –158 = 267.

The problem can be worked using a chart where enough space is left between the minuend and subtrahend so exchanges can be made in the minuend. Notice the steps shown if you work this problem using a Base chart as shown below.

Now, we'll perform this basic algorithm in different bases. Pay attention to the base when you subtract! For instance, in the first example below you have to exchange a flat for 9 more longs (since it is Base Nine). One way to show this is to actually add 9 (the base) to the amount of longs already there, so I cross off the 5, and add 9 to get 14. If you write it that way, remember the number you are writing is in Base Ten and not in the Base you are working in. Writing it this way is probably easiest when you first start to subtract. A more elegant way is to write it the same way you do when working in Base Ten, which is by putting a 1 in front of the 5 in the longs column so it looks like 15 (it doesn't mean fifteen), which in Base Nine represents 14 longs (5 longs + 9 more from the exchange)! Both ways of writing it are shown. You might want to use your Base Blocks to help visualize the actual exchanges being made. Study the following examples. Check each answer by adding the answer to the subtrahend and see that you get the minuend!

Example 1

\(\begin{aligned} 253_{\text{nine}} \\ \underline{-182_{\text{nine}}} \end{aligned}\)

Example 2

\(\begin{aligned} 3\text{E}1_{\text{twelve}} \\ \underline{-14\text{T}_{\text{twelve}}} \end{aligned}\)

Example 3

\(\begin{aligned} 402_{\text{five}} \\ \underline{-233_{\text{five}}} \end{aligned}\)

Example 4

\(\begin{aligned} 1010_{\text{two}} \\ \underline{-111_{\text{two}}} \end{aligned}\)

Check: \(\begin{aligned} 11_{\text{two}} \\ \underline{+111_{\text{two}}} \\ 1010_{\text{two}} \end{aligned}\)

In Examples 3 and 4, when I needed to make an exchange and there was a zero in the place value to the left, the exchange had to be made at a higher place value first. Then, exchanges are made down the line until you can subtract. This case happens in Base Ten all the time when you subtract a number from 100, 1000, 10000, etc. Most people just start crossing off each zero and putting 9's above them out of habit, without having any idea why they are doing it. To subtract 235 from 1000, first you should cross off the 1, put a zero above it and put a 1 in front of the zero in the hundred's place (which is trading in 1000 for 10 hundreds), then you should cross off that 10 in the hundred's place, put a 9 above it and put a 1 in front of the zero in the ten's place (which is exchanging 10 hundreds for 9 hundreds and 10 tens), then you should cross off that 10, put a 9 above it and a 1 in front of the zero in the one's place (which is exchanging 10 tens for 9 tens and 10 ones). Then, you can subtract as shown in the example to the right. It's important to really understand what's going on here because children usually have a very hard time when there is a zero to cross off.

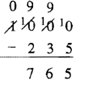
Exercise 1

Perform the following subtraction problems. You can use blocks or charts to help visualize the problem, but you eventually want to work toward being able to do them without the manipulatives. Underneath each problem, check by adding the difference (answer) to the subtrahend (number being subtracted) and see if the sum is the minuend (the number on top). Use any addition algorithm you prefer.

a. \(\begin{aligned} 4 5 2_{\text{thirteen}} \\ \underline{-1 3 \text{E}_{\text{thirteen}}} \end{aligned}\)

b. \(\begin{aligned} 8 3 1_{\text{nine}} \\ \underline{-6 7 0_{\text{nine}}} \end{aligned}\)

c. \(\begin{aligned} 2 0 0 4_{\text{six}} \\ \underline{-3 3 5_{\text{six}}} \end{aligned}\)

d. \(\begin{aligned} 4 2 1_{\text{five}} \\ \underline{-2 3 2_{\text{five}}} \end{aligned}\)

e. \(\begin{aligned} 1 0 0_{\text{three}} \\ \underline{-1 1_{\text{three}}} \end{aligned}\)

Check each problem here:

a.

b.

c.

d.

e.

The traditional, standard subtraction algorithm is not necessarily the best one and there are many other ones you'll be learning in the rest of this Exercise Set.

The next algorithm was taught to many people before the "new math" and so I call it the Oldtimer's Algorithm. It's similar to the Standard Algorithm in that you start on the right and move to the left. But you don't regroup (formally known as borrowing). First look again at an example of using the Standard Algorithm to subtract 95 – 28. Since, you can't subtract 8 from 5, you regroup from the 9 by crossing out the 9 and writing 8 so you can put a 1 in front of the 2. Now, in the unit's column, 15 – 8 = 7 and in the ten's column, 8 – 2 = 6. The answer is 67. This new method starts out the same way. You can't subtract 8 from 5, but instead of regrouping from the 9, you add a 1 to the number under the 9, and put a 1 in front of the 5. Notice that in the unit's column, 15 – 8 = 7 and in the ten's column, instead of 8 –2, you have 9 –3 which is the same answer of 6. The advantage of this method is if you put a 1 at the top of one column, you compensate by adding a 1 to the bottom of the next column. You don't have to worry about crossing things off and making a mess and you don't have to think about the digit in the column to the left until you go to that column to subtract – no trying to regroup and getting hung up there! Look at the two methods side by side. If you use the new method, you have to leave space between the subtrahend and subtraction bar in case you need to put a 1 there.

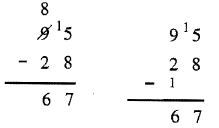
What I really like about the Oldtimer's method is that it is much easier to check. Just add up each column. There is no carrying : 7 + 8 = 15 and 6 + 1 + 2 = 9. It's a breeze. To check the Standard Algorithm, well it's something of a mess and you would need to write it down somewhere else and check it. Study the following examples.

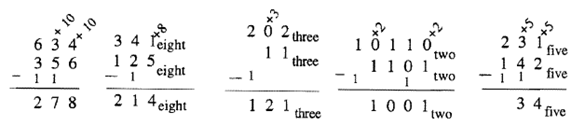
You still have to be very careful to pay close attention to the base. When you put a 1 in front of a digit, remember that it stands for the number that is the base. Another way to indicate the same thing is to write out what it stands for as shown below. The same five examples are illustrated again doing it this way. It's not as elegant but if it helps drive home what is really going on, do it this way.

Exercise 2

Subtract the following using the Oldtimer's Algorithm. Check your answers by adding up.

a. \(\begin{aligned} 5 0 3 6 \\ \underline{-3 4 1 8} \end{aligned}\)	b. \(\begin{aligned} 314_{\text{four}} \\ \underline{-221_{\text{four}}} \end{aligned}\)	c. \(\begin{aligned} 5 \text{T} 2_{\text{twelve}} \\ \underline{-2 3 \text{E}_{\text{twelve}}} \end{aligned}\)	d. \(\begin{aligned} 4 1 3_{\text{six}} \\ \underline{-3 2 4_{\text{six}}} \end{aligned}\)	e. \(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-1 0 1_{\text{two}}} \end{aligned}\)
f. \(\begin{aligned} 537_{\text{nine}} \\ \underline{-273_{\text{nine}}} \end{aligned}\)	g. \(\begin{aligned} 312_{\text{five}} \\ \underline{-224_{\text{five}}} \end{aligned}\)	h. \(\begin{aligned} 502_{\text{seven}} \\ \underline{-235_{\text{seven}}} \end{aligned}\)	i. \(\begin{aligned} 200_{\text{three}} \\ \underline{-121_{\text{three}}} \end{aligned}\)	j. \(\begin{aligned} 523_{\text{eight}} \\ \underline{-265_{\text{eight}}} \end{aligned}\)

Now that you have mastered that algorithm, here is another one for you. This is a Left to Right Algorithm where no regrouping takes place until the end of the problem – you regroup from the answer! Here's how it works. Start with the left-most column and subtract. Move to the next column. Subtract if possible. If you need to regroup, put a 1 in front of the top digit as usual, and put a slash through the previous digit in the answer. You'll take away from the answer in the end. Continue on to the next column until you've done the unit's column. Then go back and subtract one from all digits with a slash through them. Study the following example which is shown step by step.

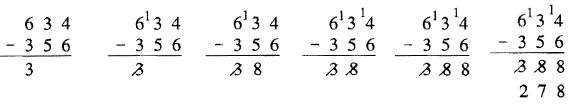
Here are some examples in other bases. If you prefer, instead of putting the 1 in front of the digit when you regroup, you can put, for example, +4 if it's in Base Four, like was shown for the previous algorithm on the bottom of the last page.

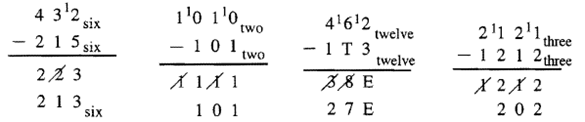
Exercise 3

Check the above examples by doing the following addition problems.

\(\begin{aligned} 213_{\text{six}} \\ \underline{+215_{\text{six}}} \end{aligned}\)

\(\begin{aligned} 101_{\text{two}} \\ \underline{+101_{\text{two}}} \end{aligned}\)

\(\begin{aligned} 2 7 \text{E}_{\text{twelve}} \\ \underline{+1 \text{T} 3_{\text{twelve}}} \end{aligned}\)

\(\begin{aligned} 202_{\text{three}} \\ \underline{+1212_{\text{three}}} \end{aligned}\)

Exercise 4

Subtract the following using the Left to Right Algorithm..

a. \(\begin{aligned} 8 0 4 2 \\ \underline{-1 3 2 5} \end{aligned}\)

b. \(\begin{aligned} 4132_{\text{five}} \\ \underline{-2413_{\text{five}}} \end{aligned}\)

c. \(\begin{aligned} 7210_{\text{eight}} \\ \underline{-5564_{\text{eight}}} \end{aligned}\)

d. \(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{-569_{\text{thirteen}}} \end{aligned}\)

e. \(\begin{aligned} 1 1 0 1_{\text{two}} \\ \underline{-1 1_{\text{two}}} \end{aligned}\)

Exercise 5

Check the answers to Exercise 4 by doing the corresponding addition problem

In this algorithm, there is one more little detail. If you cross out a zero, you must continue crossing off the digit to the left of the zero. If there is more than one zero in a row as you go left, cross off each zero until you get to a nonzero digit. Then, subtract 1 from each number crossed off as before. Pay attention to the base: In the second example below, the number before 40five is 34five. In the third example, the number before 100two is 11two. Study the following examples.

Exercise 6

Subtract the following using the Left to Right Algorithm.

a. \(\begin{aligned} 8 0 4 2 \\ \underline{-1 3 4 5} \end{aligned}\)

b. \(\begin{aligned} 4132_{\text{five}} \\ \underline{-2433_{\text{five}}} \end{aligned}\)

c. \(\begin{aligned} 7210_{\text{eight}} \\ \underline{-5214_{\text{eight}}} \end{aligned}\)

d. \(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{-539_{\text{thirteen}}} \end{aligned}\)

e. \(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-10 1_{\text{two}}} \end{aligned}\)

Exercise 7

Check the answers to Exercise 6 by doing the corresponding addition problem.

Algebra will help you understand the next algorithm:

M – S = M – S + x – x = M + x – S – x = (M + x) – (S + x)

M – S = M – S + x – x = M – x – S + x = (M –x) – (S – x)

Basically, this states that to subtract two numbers, M (minuend) and S (subtrahend), you get the same answer if you first add (or subtract) the same number to both M and S before subtracting. The Oldtimer's Algorithm works because of this fact. For instance, when you put a 1 in front of the minuend's unit's digit and a 1 below the subtrahend's ten's digit, you are adding both a 10 to the minuend and to the subtrahend; then, you subtract.

This algorithm is particularly useful if the minuend has a string of zeros at the end. Subtract 1 from the minuend and subtrahend first and then do the subtraction. Look at how this works:

\(\begin{aligned} 100000 && && 99999 \\ \underline{–65378} && && \underline{–65377} \\ 34622 &&= && 34622 \end{aligned}\)

\(\begin{aligned} 3000 && && 2999\\ \underline{–1264} && && \underline{–1263} \\ 1736 && = && 1736 \end{aligned}\)

Well, what do you think? Isn't the second subtraction shown in each pair easier to do than the first one? I just subtracted 1 from the minuend and subtrahend first!

Exercise 8

Make up two of your own subtraction problems using this method to subtract.

This algorithm also works well if the subtrahend is close to a power of the base, like 100, 1000, etc. For instance, for the subtraction problem 4503 – 997, add 3 to the minuend and subtrahend so that the problem becomes 4506 – 1000 = 3506. In the Base Four problem, \(2302_{\text{four}} – 333_{\text{four}}\), add 1 to both to get \(2303_{\text{four}} – 1000_{\text{four}} = 1303_{\text{four}}\)

Exercise 9

Make up two of your own subtraction problems using this method to subtract. Use a base other than 10.

The above method is sometimes called the Complementary Method. There is yet a more specific approach called the Complementary Algorithm. It relies on the idea of complements that we defined in an earlier exercise set. In Base Ten, pairs of complements were 1 & 9, 2 & 8, 3 & 7, 4 & 6 and 5 & 5. For the complementary method, you find a very specific complement of the subtrahend and add it to both the minuend and subtrahend before subtracting. The complement, in this case, is a 1 followed only by zeros such that the number of zeros is the same number of digits in the minuend. First, you'll have to come up with an easy way to find the complement of a given number.

Below are examples showing how to find the complement (C) of a given number (A), given you want A + C to add up to a number B.

Example 1

A = 74 and B = 1000.

Solution

To find C, add 6 to 74 to get 80, then 20 to get 100 and 900 to get 1000. C = 926.

Example 2

A = \(24_{\text{six}}\) and B = \(1000_{\text{six}}\).

Solution

To find C, add 2 units to get 3 longs, then 3 longs to get 1 flat and 5 flats to get 1 block. Then C = \(532_{\text{six}}\).

There are other ways to figure out the complement. For instance, in Base Ten, if A is 28403 and you want a C such that A + C = 1000000, you can find the answer by writing the actual complement of 3, which is 7, for the unit's digit. Move to the left. You want a digit for each place value that when added to the digit there gives a sum of 9. Do this until the number has as many digits as there are zeros in 1000000. In this case, the answer is 971597. It's harder to explain than do! If you have your own way of figuring out the complement, that's great! Don't keep it a secret.

Exercise 10

Find the complement (C) of the given number (A) such that A + C = B.

a. A = 538 and B = 10000

b. A = \(212_{\text{four}}\) and B = \(1000_{\text{four}}\)

c. A = \(1011_{\text{two}}\) and B = \(10000_{\text{two}}\)

Here is how this complementary method works. Consider the problem 452 – 74. We need to find the number that when added to 74 is 1000. How do you choose what it should add up to, as in 1000? If the first number (minuend) is a 2 digit numeral, you want a 1 with 2 zeroes (100). If the first number (minuend) is a 3 digit numeral, you want a 1 with 3 zeroes (1000), and so on. This step is the same in all bases. Back to the problem: 452 – 74: 926 is what should be added to 74 to get 1000 (from Example 1). Add 926 to the minuend and subtrahend to get the new subtraction problem which is: 1378 – 1000 = 378. The answer is the new minuend without the first digit: 378. Pretty wild! Look at \(402_{\text{six}} –24_{\text{six}}\). We need to find the number that when added to \(24_{\text{six}}\) is \(1000_{\text{six}}\)., which is \(532_{\text{six}}\) from Example 2. Add \(532_{\text{six}}\) to the minuend and subtrahend to get the new subtraction problem which is \(1304 – 1000_{\text{six}} = 304_{\text{six}}\). Again, the answer is the new minuend without the first digit: \(304_{\text{six}}\). So here's the trick – Just add the complement to the minuend, take off the first digit and that's the answer! There is no subtracting.

Example 3

Subtract using the complementary method: 912 – 573

Solution

427 is the number that when added to 573 equals 1000. Add to the minuend: 427 + 912 = 1339. Take off the first digit and the answer is 339.

Example 4

Subtract \(301_{\text{four}} – 212_{\text{four}}\) using the complementary algorithm.

Solution

From 10.b., the complement is \(122_{\text{four}}\). \(301_{\text{four}} + 122_{\text{four}} = 1023_{\text{four}}\).
So the answer is \(23_{\text{four}}\).

Exercise 11

Subtract \(1100_{\text{two}} – 1011_{\text{two}}\) using the complementary algorithm and your answer from 10.c.

Exercise 12

Perform the following subtraction problems using the complementary method.

a. \(\begin{aligned} 5034 \\ \underline{–357} \end{aligned}\)

b. \(\begin{aligned} 420_{\text{five}} \\ \underline{–231_{\text{five}}} \end{aligned}\)

The complementary method is actually easier to do with the blocks –once you get the hang of it. Take out your Base Three blocks to do the following example and problems.

To compute \(212_{\text{three}} – 120_{\text{three}}\), represent \(212_{\text{three}}\) and \(120_{\text{three}}\) with the blocks as shown below.

The minuend is shown on the left. Since its biggest "block" is a flat, the next "place value" up a block. So the problem is to figure out what needs to be added to the subtrahend (shown on the right) to make a block. It would be 1 more long and 1 more flat. In other words, if you added a long and flat to the subtrahend, you would have a block, right? Add that same amount to the minuend, shown on the left above. It should look like this:

If you subtract now, the answer is the new minuend with the largest block removed. Therefore, the answer is 2 longs and 2 units, or \(22_{\text{three}}\) The crucial step is to figure out what needs to be added to the subtrahend to make the block. Then, also add it to the minuend, remove the largest block from the new minuend and that's the answer! Ta da!

Since drawing the blocks out is sometimes cumbersome, another way to pictorially show what is going on is to use abbreviated pictures for the Base Three blocks, flats, longs and units (3B, 3F, 3L, U) as shown below.

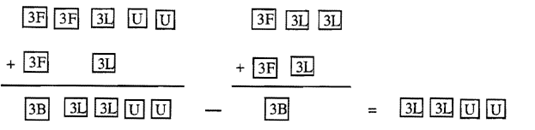
Exercise 13

On the next page, use the appropriate base blocks to subtract \(120_{\text{three}} - 12_{\text{three}}\) and \(213_{\text{four}} - 133_{\text{four}}\) using the complementary method. Explain how to do it and show full or abbreviated pictures with the base blocks.

a. Use Base Three Blocks and complementary method to subtract \(120_{\text{three}} – 12_{\text{three}}\).

b. Use Base Four Blocks and complementary method to subtract \(213_{\text{four}} – 133_{\text{four}}\).

Exercise 14

Explain how each student is doing the subtraction problem 634 – 152.

a. Mary does the subtraction in her head by thinking out loud "534, 484, 482". What is her reasoning?

b. Pedro does the subtraction by thinking out loud " 634 and 48 is 682, take away 200 is 482". What is his reasoning?

Another method to subtract is called the Subtract from the Base Algorithm. This one is especially nice for working in other bases. In this method you never need to subtract from a number larger than the base.

Standard algorithm:

\(\begin{aligned} 534 \\ \underline{-256} \end{aligned}\) make exchanges \(\begin{aligned} {}^{4}&& {}^{12} &&{}^{14} \\ \cancel{5} &&\cancel{3}&&4 \\ -2&&5&&6 \\ \hline 2&&7&&8 \end{aligned}\)

Using the Subtract from the Base method if you have a place where the bottom number is bigger than the top number, regroup as in the traditional method then subtract the bottom number from the base and add the result to the top number. The advantage of this method is you never subtract a number from any number larger than the base. This is a good method for people who need to use fingers to subtract.

Subtract from the base algorithm:

When using this method in other bases circle the base number when regrouping. For example when working in base six, 6 does not exist and writing 10 can be confusing even though it is correct.

Exercise 15

Subtract the following using the Subtract from the Base Algorithm. These are the same problems from #6. Don’t forget to circle the base number when regrouping.

a. \(\begin{aligned} 8 0 4 2 \\ \underline{-1345} \end{aligned}\)

b. \(\begin{aligned} 4 1 3 2_{\text{five}} \\ \underline{-2433_{\text{five}} } \end{aligned}\)

c. \(\begin{aligned} 7 2 1 0_{\text{eight}} \\ \underline{ -5214_{\text{eight}}} \end{aligned}\)

d. \(\begin{aligned} \text{T} 3 7_{\text{thirteen}} \\ \underline{ -539_{\text{thirteen}}} \end{aligned}\)

e. \(\begin{aligned} 1 1 0 0_{\text{two}} \\ \underline{-101_{\text{two}} } \end{aligned}\)

Do you know of another algorithm for addition or subtraction? If so, post it with an explanation on the Forum for extra credit.