8.1: Addition and Subtraction

You will need: Positive and Negative Counters (Material Cards 18A and 18B)

Remember that whole numbers are made up of zero and the counting numbers: 0, 1, 2, 3, 4, 5, . . . When school children first see a number line, they usually focus on the whole numbers and the number line looks something like this:

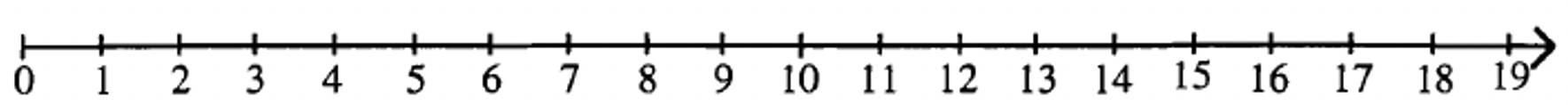
In this model, the number line starts at zero, and the arrow to the right indicates that it goes on indefinitely to the right. Actually, there are infinitely many numbers (or points) between any two numbers on the number line. For example, a few of the infinite number of points between 1 and 2 are 3/2, 4/3, 5/4, 6/5, 7/5, 8/5, etc. On the number line, there are infinitely many irrational numbers as well. Irrational numbers cannot be written as the ratio of two whole numbers, like the way we represent reduced fractions. Examples of some irrational numbers between 3 and 4 are \(\sqrt{11}\), \(\sqrt{15}\), 3.10110111..., and \(\pi\). Contrary to popular belief, \(\pi\) does not equal 3.14 and \(\pi\). does not equal 22/7. Both 3.14 and 22/7 are rational numbers (unlike \(\pi\) which is an irrational number, NOT a rational number) and 3.14 and 22/7 are only approximations commonly used when calculating with \(\pi\). Irrational numbers will be explored and discussed in more detail in a different module.

Okay, let's get back to our discussion of the number line. The number line shown at the beginning of this exercise set is really only a half-line, so to call it a number line is really a misnomer. A horizontal line goes on indefinitely in both the left and right direction, not just to the right. Numbers to the right of zero are called positive numbers. Numbers to the left of zero are called negative numbers. Zero is the only number that has no sign – it is neither positive, nor negative. For each positive number, there is a corresponding negative number, which on a given number line, is the same distance from zero as the positive number, but it is to the left side of zero. Numbers the same distance from but on opposite sides of zero are called "opposites." Negative numbers are represented like this: -5 is read "negative five", -20 is read "negative twenty", etc. So, 5 and -5 are opposites, 20 and -20 are opposites, and zero is the opposite of itself.

Exercise 1

For each marking on the number line, fill in the missing numbers

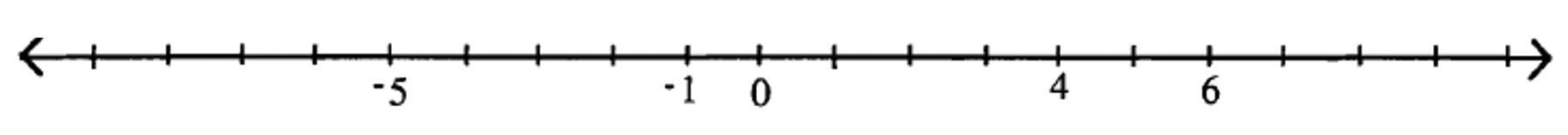
Definitions: The set of positive integers (which are also commonly called the natural numbers or counting numbers) is written as: {1, 2, 3, 4, ... }. Positive numbers may also be written with a positive sign before it. For instance, 4 may be written a +4.

The set of whole numbers contains both zero and the natural numbers and is written as: {0, 1, 2, 3, ... }.

Definition: The set of negative integers contains exactly all the opposites of all the positive integers.

1. Write the set of negative integers:

Definition: The set of integers is made up of zero, the positive integers and the negative integers.

2. Write the set of integers:

Definition: The absolute value of a number on the number line is defined to be the distance that point is from zero. Since absolute value is defined in terms of distance, it can never be negative. To evaluate the absolute value of a number, state the distance it is from zero.

Examples

The absolute value of 5 is 5, since the distance from 5 to 0 is 5 units. The absolute value of -5 is also 5, since the distance from -5 to 0 is also 5 units.

Exercise 3

Evaluate the absolute value of each of the following numbers:

a. 4: ____

b. -8: ____

c. 2: ____

d. -1: ____

e . 0: ____

To indicate the absolute value of a number, we enclose it between two vertical lines. "The absolute value of -15 is 15" is written like this: | -15 | = 15. In order to simplify a problem with an absolute value sign, the part inside the absolute value sign must be simplified first. So, if the part inside the absolute value sign is not simply a numeral, think of the part inside as being in parentheses, and simplify it first. Then, take the absolute value of the numeral. You'll have to do this for part c and f of exercise 4.

Exercise 4

Simplify each of the following:

a. | 7 | = ______		c. | 7 – 3 | = _______
d. \(|\frac{3}{7}|\) = ______	e. \(|-\frac{3}{7}|\) = ______	f. | 2\(\cdot\)5 – 4 | = _______

Exercise 5

Write two numerals that have an absolute value of 6 ______ and _______

Exercise 6

Write two numerals that have an absolute value of 19 ______ and ______

Exercise 7

Write all numerals that have an absolute value of zero _______

Exercise 8

Write all numerals that have an absolute value of -10 (negative 10) _______

Each positive and negative number can be represented with a directed line segment called a vector.

Basically, a vector looks like an arrow. It has two properties: it has a certain length (called the "magnitude") and it points in a certain direction. Since we'll be using horizontal number lines, we'll be drawing horizontal vectors. An arrow pointing to the right will denote a positive number and an arrow pointing to the left will denote a negative number.

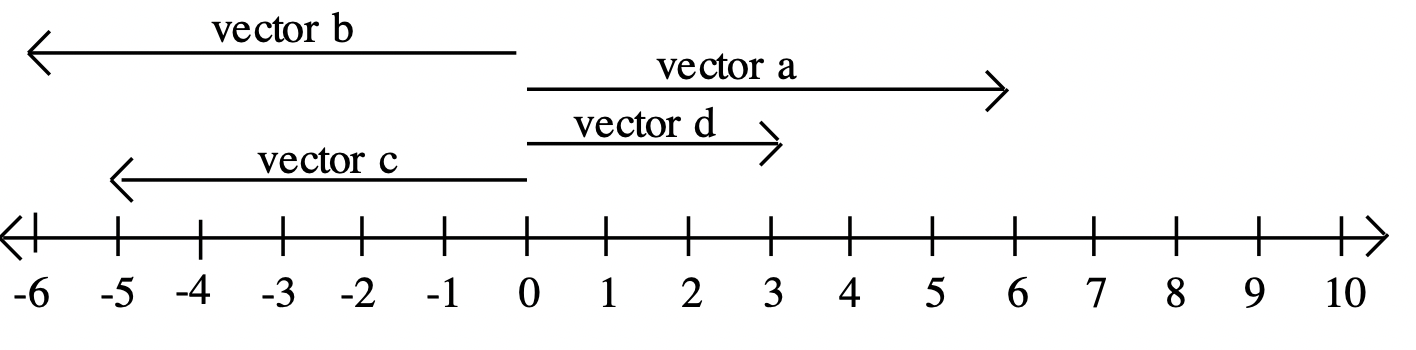
Below is a number line, with some vectors shown above. Vector a is 6 units long and the arrow points to the right. Therefore, it represents the number +6. Vector b is also 6 units long, but it points to the left. Therefore, it represents the number -6. Both vectors have a magnitude of 6.

Exercise 9

1. What number does vector c represent? _________
2. What number does vector d represent? _________

Each vector has an initial point (the starting point of the vector) and a terminal point (the ending point, where the arrow is shown). If the initial point of the vector is placed at zero, the number line can be used as a convenient marker – the terminal point of the vector is simply placed on the number being represented. But it isn't necessary to represent it that way, as you could see from all the vectors shown in the above examples. Vectors a, b, c and d could have been drawn with the initial point at zero as shown below. If you draw a vector with its initial point at zero, the number that vector represents is simply the same number on the number line where its terminal point lands.

Another way of thinking about numbers is to think of them in terms of "actions". You could think of the number "5" as the action of moving 5 spaces to the right. When you draw the vector representing 5, that is a way of showing that particular action. You could think of the number "-3" as the action of moving 3 spaces to the left. When you draw the vector representing -3, that is a way of showing that particular action.

The number line, along with this idea of thinking about numbers in terms of actions, can be used to add numbers together.

Definition: To add two numbers, m and n, you DO the first action, m. The addition sign means NOW DO the second action, n. The answer to the problem (which is the sum: m + n) is the single action that could have been done to achieve the same result as doing the separate actions in succession.

Consider this practical way of thinking about it. Think of walking east as representing a positive number and walking west as representing a negative number. If you walked 5 blocks east, then 7 blocks west, then 3 blocks east, you would be one block east of your original starting point. This can be a way to think about the problem: 5 + (-7) + 3 = 1.

Procedure for using vectors as actions to add two numbers, m and n

1. Pick a starting point and draw the vector m (which is a way of representing the action of m) with its initial point at the designated starting point.
2. The addition sign means starting at the terminal point of the previous action DO the next action. So, draw the vector n, placing the initial point of n at the terminal point of vector m.
3. The sum, m + n, is the same number that would be represented by a vector with its initial point placed on the original starting point and its terminal point on the final terminal point after the last action took place.

For CONVENIENCE only, it is easiest to always use a number line and pick zero as the initial starting point. By doing that, the answer to the problem will be wherever the terminal point of the last action landed on the number line.

Before going on, it is important to note that it is not necessary to mark every point on a number line. In fact, this is impossible since there are infinitely many points on a number line. However, it is usually a good idea to mark zero and at least one point on either side of zero. Mark the number line in a way that makes it convenient to do the problem.

We'll use the above procedure to add the following numbers. For these examples and for the exercises, start at zero for convenience. Draw the first vector. Then move up a little to draw the second vector so it is obvious which vector was drawn first and which one was drawn last. There should be one vector shown for each number in the sum. Since we are placing the initial point of the first vector on zero, we can state the answer by noting where the terminal point of the last vector landed on the number line.

Example: \(4 + 2\)

4 + 2.

Solution

Starting at zero, DO the action 4 (which is shown by drawing the vector representing 4), then starting at the point where the first action ended, DO the action 2 (shown by drawing the vector representing 2).

The answer is 6 since the terminal point of the last vector landed on 6.

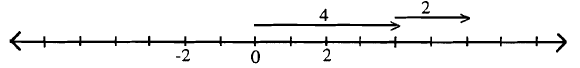
Example: \(-5 + 3\)

-5 + 3.

Solution

Starting at zero, DO the action -5 (which is shown by drawing the vector representing -5), then DO the action 3 (shown by drawing the vector representing 3).

The answer is -2 since the terminal point of the last vector landed on -2.

Example: \(-3 + -4\)

-3 + -4.

Solution

Starting at zero, DO the action -3 (shown by drawing the vector representing -3), then DO the action -4 (shown by drawing the vector representing -4).

The answer is -7 since the terminal point of the last vector landed on -7.

Example: \(-4 + 8\)

-4 + 8.

Solution

Starting at zero, DO the action -4 (which is shown by drawing the vector representing -4), then DO the action 8 (shown by drawing the vector representing 8).

The answer is 4 since the terminal point of the last vector landed on 4.

Example: \(50 + -35\)

50 + -35.

Starting at zero, DO the action 50 (shown by drawing the vector representing 50), then DO the action -35 (shown by drawing the vector representing -35).

The answer is 15 since the terminal point of the last vector landed on 15.

It is IMPERATIVE that you LABEL your number line. Otherwise, it is not clear what each vector represents. Do not assume that each mark stands for 1 unit. Without the label of at least one number on each side of zero on the last example, one might assume the last example shown represented 10 + -7 and that the answer was 3.

Exercise 10

Use vectors on the number line to add the following numbers together. Mark and LABEL your number line with at least zero and a point on either side.

Here is an example of how to do the following problems:

-4 + 8 + (-5) = -1 since the terminal point of the last vector landed on -1.

a. 5 + (-8) = _____ since ______________________________________________

b. -7 + (-2) = _____ since _____________________________________________

c. -5 + 9 = _____ since _____________________________________________

d. 7 + (-6) = _____ since ______________________________________________

e. -7 + 5 = _____ since ______________________________________________

f. -100 + 40 = _____ since ______________________________________________

g. -3 + (-2) + 4 = _____ since ___________________________________________

h. 4 + (-12) + 5 = _____ since ______________________________________________

Sometimes, you'll see vertical number lines instead of horizontal number lines. In this case, the positive numbers go up, and are represented by vertical vectors with the arrow pointing up. Likewise, negative numbers go down and are represented by vertical vectors pointing down. An example of a vertical number line is shown on the right.

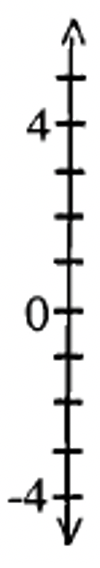
Exercise 11

There is a common use of using a vertical number line. Can you think of one? See if you can think of any and write any down here.

If you need a hint for Exercise 11, think about the weather.

We'll continue to think about actions as we use vectors to do subtraction problems.

Definition: To subtract a number, m, you UNDO the action, m which means you DO the OPPOSITE of the action m.

Whether or not you are doing a subtraction problem, an addition problem, or both in the same problem, the answer to the problem is the single action that could have been done to achieve the same result as doing the separate actions in succession.

You can think of subtraction as undoing some mistake.

Consider a variation on the original example given for addition. To refresh your memory, here was that problem: Think of walking east as representing a positive number and walking west as representing a negative number. If you walked 5 blocks east, then 7 blocks west, then 3 blocks east, you would be one block east of your original starting point. This can be a way to think about the problem: 5 + (-7) + 3 = 1.

Exercise 12

Imagine you walked 5 blocks east, then 2 blocks west, and then realized you had made a mistake. You weren't supposed to walk 2 blocks west. You would need to undo that mistake. What would you do to undo that mistake and get back to where you were before you walked 2 blocks west on accident?

In exercise 12, I hope you realized you needed to walk 2 blocks east to undo your mistake. To translate the steps taken in #12, we could write 5 + (-2) – (-2) = 5. Here is how we would explain and show the actions using vectors on the number line.

5 + (-2) – (-2): Starting at zero, DO the action 5 (shown by drawing the vector representing 5), then DO the action -2 (shown by drawing the vector representing -2), then UNDO the action of -2 (which means to DO the OPPOSITE of the action -2, which is to DO the action +2, shown by drawing the vector representing +2).

The answer is 5 since the terminal point of the last vector landed on 5.

Procedure for using vectors to add or subtract two numbers:

1. If the first number is m, pick a starting point and draw vector m (which is a way of representing the action m) with its initial point at the designated starting point.
2. If the next sign is addition, DO the next action by drawing the vector representing the next number, placing the initial point of this vector at the terminal point of the previous vector. If, on the other hand, the next sign is subtraction, UNDO the next action. So, draw the vector representing the opposite of the next number, placing the initial point of this vector at the terminal point of the previous vector.
3. If there is another addition or subtraction sign, go back to step 2. Otherwise, at this point, we can find the answer. The answer is the same number that would be represented by a vector with its initial point placed on the original starting point and its terminal point on the final terminal point after the last action took place.

Again, using zero as the starting point is CONVENIENT because the answer to the problem will be wherever the terminal point of the last action landed on the number line.

We'll use the above procedure to compute the following problems. For these examples and for the exercises, start at zero for convenience. Draw the first vector. Then move up a little to draw the second vector so it is obvious which vector was drawn first and which one was drawn last. There should be one vector shown for each number in the problem. Since we are placing the initial point of the first vector on zero, we can state the answer by noting where the terminal point of the last vector landed on the number line.

Example

4 – (-2).

Solution

Starting at zero, DO the action 4 (which is shown by drawing the vector representing 4), then UNDO the action -2 (which means to DO the OPPOSITE of the action -2, which is to DO the action +2, shown by drawing the vector representing +2).

The answer is 6 since the terminal point of the last vector landed on 6.

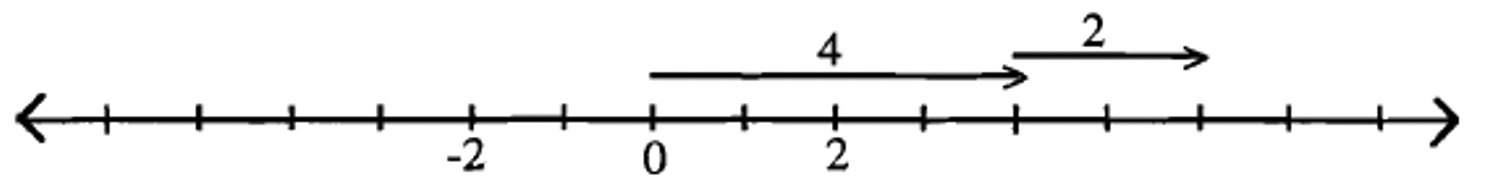
Example

-5 – (-3).

Solution

Starting at zero, DO the action -5 (shown by drawing the vector representing -5), then UNDO the action -3 (which means to DO the OPPOSITE of the action -3, which is to DO the action +3, shown by drawing the vector representing +3).

The answer is -2 since the terminal point of the last vector landed on -2.

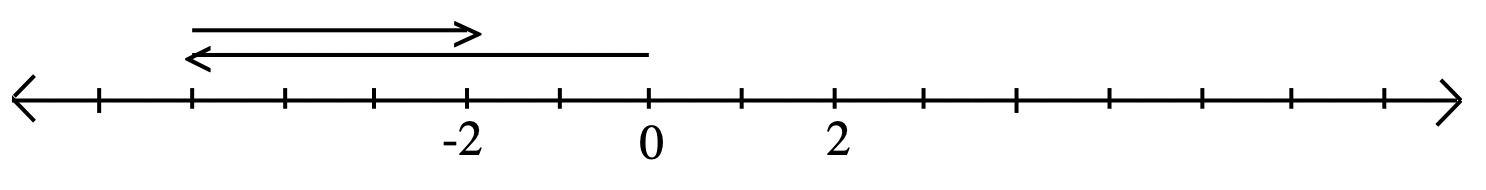
Example

-3 – (+4).

Solution

Starting at zero, DO the action -3 (shown by drawing the vector representing -3), then UNDO the action +4 (which means to DO the OPPOSITE of the action +4, which is to DO the action -4, shown by drawing the vector representing -4).

The answer is -7 since the terminal point of the last vector landed on -7.

Example

-4 – (-8).

Solution

Starting at zero, DO the action -4 (shown by drawing the vector representing -4), then UNDO the action -8 (which means to DO the OPPOSITE of the action -8, which is to DO the action +8, shown by drawing the vector representing +8).

The answer is 4 since the terminal point of the last vector landed on 4.

Example

50 + (-35).

Solution

Starting at zero, DO the action 50 (shown by drawing the vector representing 50), then DO the action -35 (shown by drawing the vector representing -35).

The answer is 15 since the terminal point of the last vector landed on 15.

It is IMPERATIVE that you LABEL your number line. Otherwise, it is not clear what each vector represents. Do not assume that each mark stands for 1 unit. Without the label of at least one number on each side of zero on the last example, one might assume the last example shown represented 10 + (-7) and that the answer was 3.

Exercise 13

Use vectors on the number line to add the following numbers together. Mark and LABEL your number line with at least zero and a point on either side.

Here is an example of how to do the following problems:

Example

-4 + 8 + (-5) = -1 since the terminal point of the last vector landed on -1.

a. 5 – (+8) = _____ since __________________________________________ .

b. -7 – (+2) = _____ since __________________________________________ .

c. -5 – (-9) = _____ since _____________________________________________ .

d. 7 – (+6) = _____ since __________________________________________ .

e. -7 – (-5) = _____ since __________________________________________ .

f. -100 – (-40) = _____ since __________________________________________ .

g. -3 – (+2) – (-4) = _____ since __________________________________________ .

h. 4 – (+12) + 5 = _____ since __________________________________________ .

At this point, it would be beneficial if you looked back at the examples on page 4 and 5 and compared them with the recent examples shown on page 8 and 9. The examples on page 8 and 9 include subtraction, whereas the examples on page 4 and 5 are addition problems. Using the idea of adding and subtracting using vectors and the action approach (either DO or UNDO an action), the problems when done with vectors on the number line look exactly the same. The same is true if you look at the problems in Exercise 10 and 13. Somehow, then, there seems to a connection between subtraction and addition. We'll put it all together after we explore a very different way of adding and subtracting, this time using manipulatives.

Another way to represent positive and negative numbers is by using a collection of positive and negative counters. You need to use counters of one color to represent positive numbers (each counter = +1) and counters of another color to represent negative numbers. If you use the material cards, each green square will represent +1 and each red square will represent -1. We'll discover that there are many ways to represent the same number using these counters. Get out your counters to do the following exercises.

The simplest way to represent a positive number, x, is to have a collection of x green counters. The simplest way to represent a negative number, -y, is to have a collection of y red counters. For example, 4 red counters will represent -4 and 3 green counters will represent +3. In these exercises, I'll sometimes represent a positive counter by either a square or circle with a positive sign (+) or a "G" inside, or by just a "G". Similarly, a negative counter will be represented by either a square or circle with a negative sign (-) or an "R" inside, or by just an "R".

Exercise 14

What number is represented by each of the following collections?

a.	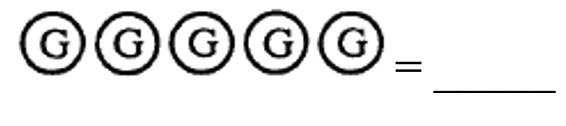b. RRRRRRRRR = ______
c.	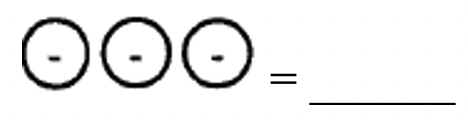d.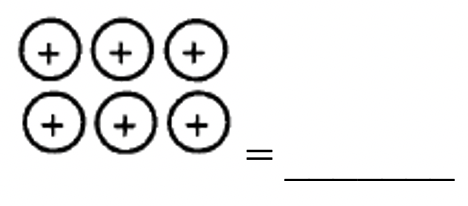

Exercise 15

Under each number, represent the number by showing a collection of counters.

b. 2

Exercise 16

What number do you think the collection below represents? ______ Explain why.

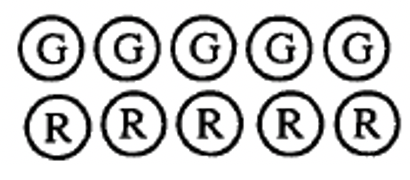
In exercise 14, there were 5 positives and 5 negatives. Did you come up with an answer of zero? If so, you're on the right track. Basically, when a positive counter is paired with a negative counter, they nullify each other. Any time there are the same number of positive counters as negative counters, you have a representation of the number, zero.

Exercise 17

Using positive and negative counters, show three different representations of zero.

a.

b.

c.

Let's see if you can figure out what number each collection represents.

Exercise 18

State the number represented by each collection

a. The collection below represents _____	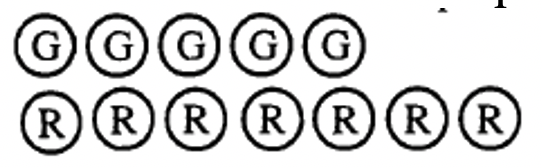b. The collection below represents _____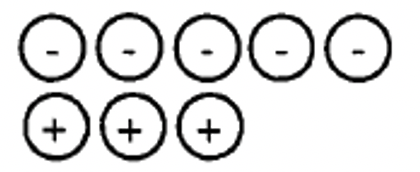
c. The collection below represents _____	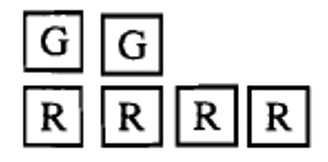d. The collection below represents _____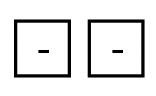
e. The collection below represents _____ RRRRRRGGG	f. The collection below represents _____ GRRGRGRRGGGGG
g. The collection below represents _____	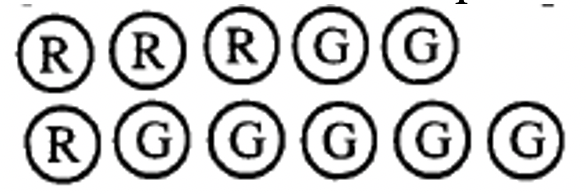h. The collection below represents _____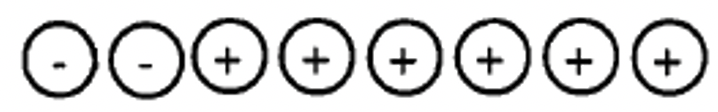

How do you think you did? Hopefully, you came up with an answer of -2 for a-d. If so, you should be convinced that different collections can represent the same number. Each pairing of a negative with a positive basically "cancels each other out". Therefore, to figure out what number a particular collection represents, simply pair as many positives with negatives as possible (red-green pairs), and remove or ignore those counters. Then, count the counters of the one "color" or "sign" that remains. You may have noticed it was easier to compute a-d because the pairings were more easily seen.

Exercise 19

Using positive and negative counters, find 3 different representations of 4. Do these with your actual positive and negative manipulatives first. Then, show it on paper.

a.

b.

c.

Exercise 20

Using positive (green) and negative (red) counters, show 3 different representations of -4. Then, show your three different representations below.

a.

b.

c.

Let's move on to how we can use the counters to add integers. To add integers, simply make a collection of counters representing each number to be added and combine the counters. Then, find the number that the resulting collection represents. Do this by first pairing off any positives and negatives and removing them from the pile.

Example

Show two different ways to use the counters to add the 4 + (-7).

First Way:

First, combine a collection representing 4 (4G) and a collection representing -7 (7R):

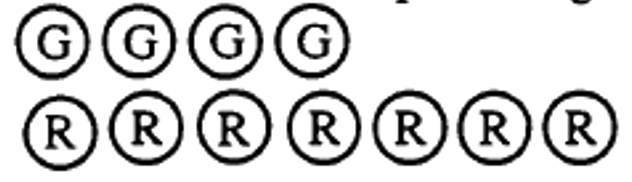
Second, remove any red-green pairs:

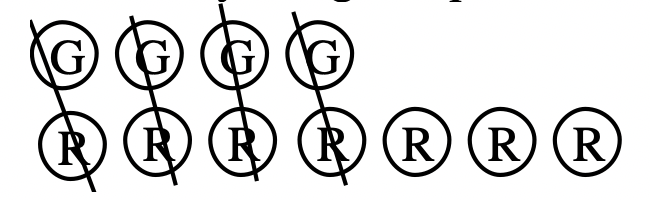
Third, count the counters remaining:

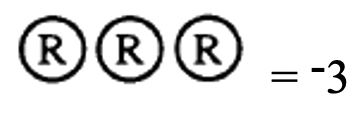
Therefore, 4 + (-7) = -3.

Second Way:

First, combine a collection representing 4 (8G and 4R) and a collection representing 7 (8R and 1G):

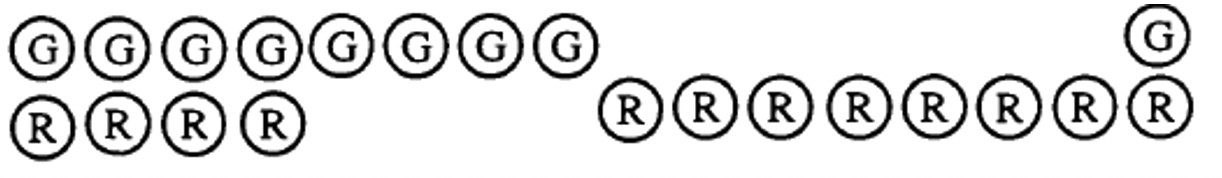
Second, remove any red-green pairs:

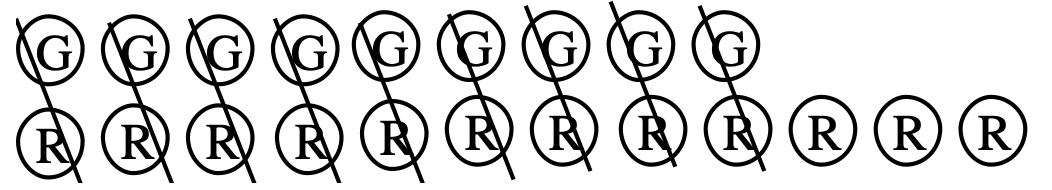
Third, count what counters are remaining:

Therefore, 4 + (-7) = -3.

Of course, the simpler and more direct method is the first way shown, but the result is the same even when complicated representations of the numbers are used in the first step.

Exercise 21

Use red and green counters to add the following integers. Do these problems using the actual manipulatives. Then, explain and show the steps below

Although subtraction is a little trickier using counters, they provide a really interesting way of showing how to subtract negative numbers.

Using the counters, m – n means remove a collection of counters representing n from a collection of counters representing m. The number that the resulting collection represents is the difference (answer).

This means we have to start with a collection of counters representing m. In order to remove a collection representing n, it must be possible to remove a collection representing n from the collection used for m. Sometimes, the original collection chosen for m will not suffice, and the collection must be altered by adding some red-green pairs to the collection representing m. Usually, we start by putting in a simple representation of m counters and see if it is possible to remove or taking away a representation of n counters. If so, we do than and find the number that the resulting collection represents. Let's try this on some examples using the physical models (manipulatives) and then practice showing it on paper.

Example: \(4-2\)

4 – 2

This means to remove a collection representing 2 from a collection representing 4.

Step 1: Make a collection representing 4 (4 green counters): \(\not{GG}\)GG

Step 2: Take out a collection representating 2 (2 green counters):

Step 3: The collection remaining ( GG ) represents 2. So, 4 – 2 = 2.

Example: \(-5-(-3)\)

-5 – (-3)

This means to remove a collection representing -3 from a collection representing -5.

Step 1: Make a collection representing -5 (5 red counters): RRRRR

Step 2: Take out a collection representing -3 (3 red counters):

Step 3: The collection remaining ( RR ) represents -2. So, -5 – (-3) = -2.

Example: \(3-5\)

3 – 5

This means to remove a collection representing 5 from a collection representing 3.

Step 1: Make a collection representing 3 (3 green counters): GGG

OH NO! The next step would be to take out a representation of 5 (5 green counters), but notice this is impossible because there are only 3 green counters to begin with. An extra step must be inserted here. We need to alter the representation of 3 so that 5 greens can be taken out. It should make sense that we can always insert some green-red pairs to the representation of 3 (each green-red pair is the effect of adding zero) without changing the representation of 3. In this example, it makes sense to add 2 more red-green pairs, so that there will be 5 greens and 2 reds in the collection. It will still be a collection representing 3. This extra step is often necessary when doing subtraction problems with integers.

Step 2: Add 2 red-green pairs to the collection representing 3: GGGRGRG

Step 3: Take out a collection representing 5 (5 green counters): \(\begin{aligned} & \fbox{GGGGG} \\ & \text{RR} \end{aligned}\)

Step 4: The collection remaining (RR) represents -2. So, 3 – 5 = -2

Exercise 22

For each problem, state what the problem means (For instance, 4 – (- 9) means remove a collection of counters representing -9 from a collection of counters representing 4), and then explain and show each step you need to take to find the answer. Each problem requires 3 or 4 steps. You should do these problems using the manipulatives, and as you do it, explain and show the steps on paper.

a. 6 – 3 This means Show all of the steps below.

b. 4 – 6 This means Show all of the steps below.

c. -7 – (- 6) This means Show all of the steps below.

d. -3 – (- 7) This means Show all of the steps below.

e. 4 – (- 3) This means Show all of the steps below.

f. -2 – 5 This means Show all of the steps below.

g. 5 – 5 This means Show all of the steps below.

h. 5 – (- 5) This means Show all of the steps below.

i. -4 – (- 4) This means Show all of the steps below.

j. -6 – 6 This means Show all of the steps below.

Exercise 23

State what the problem means in terms of using positive and negative counters and show all steps to (a) subtract 5 - 8, and then (b) add 5 + (-8).

a. 5 – 8

c. What did you notice about your answers to a and b?

Hopefully, you noticed that removing a collection representing 8 from a collection representing 5 produced the same result as combining a collection representing 5 and -8.

In other words, subtracting 8 produced the same result as adding -8.

Exercise 24

1. Use the actual manipulatives. Start with a collection of at least 4 red and some green counters and write what you have below:
2. Remove 4 red counters from your collection. Show this step by crossing out or circling 4 red counters in your collection above. After removing those red counters, what number does the collection in part a now represent? ______
3. Start over. Begin by combining the original collection you had in part a with 4 green counters (add 4 green counters to your original collection). Below, show what the collection now looks like.
4. What number does your final collection represent? ______

Exercises 21 and 22 illustrate a very important fact about subtraction. Subtracting a number gives the same result as adding the opposite number. Exercises 10 and 13, and the examples preceding each of those exercises also illustrated this fact.

Note that red and green counters, or positive and negative counters are opposites.

Example

Explain what 7 – 4 means, and then state another way to get the same result.

Solution

7 – 4 means remove a collection representing 4 from a collection representing 7. This gives the same result as combining a collection representing 7 with a collection representing the opposite of 4, which is to combine a collection representing 7 with a collection representing -4 (which means combine 7G with 4R.) So, 7 – 4 = 7 + (- 4).

Example

Explain what 2 – (- 6) means, and then state another way to get the same result.

Solution

2 – (- 6) means remove a collection representing -6 from a collection

representing 2. This gives the same result as combining a collection representing 2 with a collection representing the opposite of -6, which is to combine a collection representing 2 with a collection representing 6 (which means combine 2G with 6G.) So, 2 – (- 6) = 2 + 6.

Exercise 25

Explain what each problem means and then state another way to get the same result

b. 4 – 8

Exercise 26

Rewrite each subtraction as an equivalent addition problem.

a. 4 – 5 = _____________

Exercise 27

Rewrite each problem so it is only in terms of addition. In other words, only change each subtraction part to an equivalent addition part. Do not compute the answer.

Exercise 28

Fill in the blanks:

1. Subtracting 6 is the same as adding _____ .
2. Subtracting -8 is the same as adding _____ .
3. Subtracting a positive number is the same as adding a ______________ number, where that _____________ number is the opposite of the original positive number.
4. Subtracting a negative number is the same as adding a ______________ number, where that _____________ number is the opposite of the original negative number.
5. Subtracting a number is the same as adding the _______________ of that number.

The one thing you must pay careful attention to is the difference between the subtraction sign and the number being subtracted. When you rewrite a subtraction problem as an equivalent addition problem, you have to remember to change the number that was being

subtracted to its opposite. It is certainly not true that 6 – 3 is the same as 6 + 3. But it is true that 6 minus (positive 3) is equal to 6 plus (negative 3); or 6 – 3 = 6 + (- 3).

It isn't necessary to change subtraction problems to equivalent addition problems. It is, however, sometimes very useful because the addition problem may be easier to work with. And if all subtraction can be written as addition, then one only needs to learn rules for addition and apply them to all addition or subtraction problems. Let me say that although it's a good idea to know the rules for addition and subtraction, it's even more important to be able to go back to the basic concepts and be able to use manipulatives to understand what addition and subtraction really mean.

If you filled in the correct answer to 28e, then you've got it. The relationship between addition and subtraction lies in this fact.

Every subtraction problem can be rewritten as an equivalent addition problem. Instead of subtracting a number, you can add the opposite of that number.

Definition: Let m and n be any integer. Then, m – n = m + (- n). This is called Adding the Opposite. Remember: -n is not necessarily negative! If n is positive, -n is negative but if n happens to be negative (n is just a variable), then -n would be positive.

Let's return to the number line and using vectors in conjunction with the missing addend approach to compute a subtraction problem. Note that this is an entirely different approach from the way we did it at the beginning of the exercise set, when we did it with doing and undoing actions. First, let's review the definition of subtraction using the missing addend approach.

Definition: Subtraction (Missing Addend Approach) The difference of two numbers, m and n, written m – n is the number c such that n + c = m. In other words, if c is added to the subtrahend, n, then the sum is the minuend, m. The answer, c, is called the missing addend.

Consider the problem 7 – 3. The missing addend approach states the answer to this subtraction problem will be the number that when added to the number shown after the subtraction sign equals the number that precedes the subtraction sign. Since 3 is the number after the subtraction sign, we have to find a number to add to 3 that will give an answer of 7. Using a number line, this means if you place the initial point of a vector at 3, what vector must be drawn (the missing addend can still be thought of as which action must take place) so that the terminal point will land on 7? Draw a vector with its initial point at 3 and its terminal point at 7. Make sure the arrow on the end of the vector points to 7.

The number that the vector represents is the answer to the problem. We are trying to find that missing addend, which is the vector we draw. The illustration for 7 – 3 is shown below. The vector has length 4 and points to the right, so the answer is 4, which I've written above the vector (labeled and marked the missing addend) to indicate the answer to the problem.

Again, note that this is a completely different approach to subtraction. It is not at all like the way we did it at the beginning of the exercise set, when we did it by doing one action, and then undoing another and then seeing what one action could have achieved the same result.

Using the missing addend approach, only one vector is shown, and the number that vector represents is the answer to the problem. In other words, the vector represents the missing addend you are looking for, which is the difference of the two numbers. You can find the answer to the subtraction problem by drawing a vector, placing initial point of the vector on the subtrahend (the number shown right after the subtraction sign), and placing the terminal point on the minuend (the number preceding the subtraction sign). Note that this definition only make sense when subtracting two numbers, as opposed to adding and/or subtracting several numbers.

Procedure for subtracting two integers using vectors and the missing addend approach: To find the difference of m and n, draw a vector with its initial point on n and its terminal point on m. The vector drawn is the missing addend, and is the answer to the problem: m – n.

It's important to distinguish between the subtraction sign and the subtrahend (the number shown after the subtraction sign). Also it's important to remember to put the initial point of the vector that will represent the missing addend on the subtrahend (the number AFTER the subtraction sign, and the terminal point on the minuend (the number shown PRECEDING the subtraction sign). One method I sometimes use is to circle the minuend and subtrahend and then draw an arrow from the subtrahend to the minuend so I remember to draw the vector with its initial point on the subtrahend and its terminal point on the minuend.

Let's try the problem 2 – 9. Then, 9 + ____ = 2. Circle the minuend and subtrahend and draw an arrow from the subtrahend to the minuend before you draw the vector.

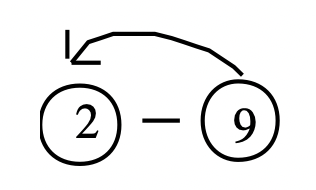
On the number line, draw a vector with its initial point at 9 and its terminal point at 2. The directed vector drawn represents the answer: -7.

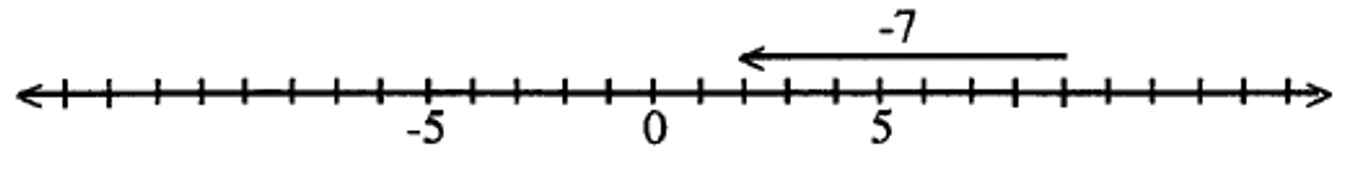
Example

12 – (- 8). Then, -8 + ____ = 12.

Circle the minuend and subtrahend and draw an arrow from the subtrahend to the minuend before you draw the vector.

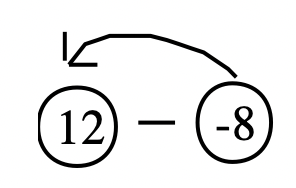
Note when you draw an arrow from the subtrahend to the minuend, the arrow points the the left in the actual subtraction problem. But that has NOTHING to do with whether or not the arrow on the vector you draw on the number line will point left or right. It points to the minuend. For this example, note that on the missing addend vector drawn below, it points to the right, and that the answer to this problem is a positive number.

Place the initial point of the vector on -8 and the terminal point on 12. The vector drawn below shows the answer: 20.

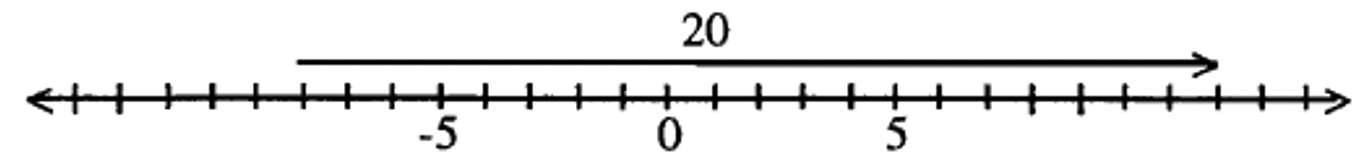
Exercise 29

Before going on, think about the possibility of using the missing addend approach and not even getting a vector.

1. In other words, what if the initial and terminal point of the vector was on the same number? It would look like a point, not a vector. When would this happen?
2. What would be the answer to a problem where this happened?

Exercise 30

Find the answer to the following subtraction problems by using vectors on the number line in conjunction with the missing addend approach. Draw an arrow from the subtrahend to the minuend as shown in the last two examples. Before drawing the missing addend representing the answer to the problem, label and mark your number line with at least 0 and one point on each side of zero. Then, draw the vector that represents the answer to each problem and label the vector with that number.

a. 10 – 4 = ______

b. -7 – 5 = ______

c. 8 – (- 3) = ______

d. -9 – (- 1) = ______

e. 3 – 10 = ______

f. -5 – (- 8) = ______

g. 6 – (- 6) = ______

h. 9 – 9 = ______

Exercise 31

By looking at the vectors a - c below, figure out what subtraction problem was being performed, and then state the answer. For instance, vector d came from doing the problem -1 – 5 since the initial point of that vector is on 5 and the terminal point is on -1. Since vector d is 6 units long and goes left, it represents the number -6. Therefore, vector d would be: -1 – 5 = -6.

a. Vector a:

b. Vector b:

c. Vector c:

One thing I love about using the missing addend model to show subtraction is that it works equally well when subtracting with larger integers. Just approximate where the integers are on the number line in relation to themselves and zero. The answer makes sense using the model.

The following examples show how to use vectors on the number line in conjunction with the missing addend approach to find these differences: 58 – 87, -130 – 55 and -130 – -55.

Example 1: \(58-87\)

58 – 87.

Solution

Draw a vector from 87 to 58. Since the vector is pointing to the left, the answer is negative and the length of the vector is 29 units long, 87 – 58. So, 58 – 87 = -29.

Example 2: \(-130-55\)

-130 – 55.

Solution

Draw a vector from 55 to -130. Since the vector is pointing to the left, the answer is negative and the length of the vector is 185 units long, since it is 130 units from -130 to 0 plus another 55 units from 0 to 55. So, -130 – 55 = -185.

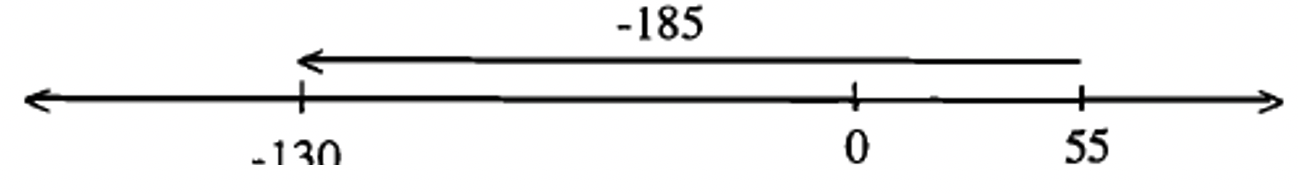
Example 3: \(-55-(-130)\)

-55 – (-130).

Draw a vector from -130 to -55. Since the vector is pointing to the right, the answer is positive and the length of the vector is 130 – 55 , or 75 units long. So, -55 – (-130) = 75.

Exercise 32

Mark and label a number line with at least zero, the minuend (the number in front of the subtraction sign) and the subtrahend (the number being subtracted). Then, use a vector to find the answer to the problem. Label the vector that is the answer

a. -92 – (-71) = _______

b. 92 – (- 81) = _______

c. -110 – (- 200) = _______

d. -122 – 76 = _______

e. 208 – 389 = _______

Finally, here are a set of rules that can always be used to add and subtract integers without the use of manipulatives. While these rules will always work, it is better to first understand where these rules came from and why they work. From doing the exercises in this exercise set, you should now have a better understanding of what it means to add and subtract with positive and negative numbers.

• Any subtraction problem can be rewritten as an equivalent addition problem using the definition of adding the opposite. Once all subtraction problems are rewritten as equivalent addition problems, there is only addition to be done, and so therefore, we only need rules for addition, which follow.
• To add numbers that have like signs (either all positive or all negative), add the absolute values of the numbers. The sign of the answer will be the sign of the original numbers.
• To add two numbers with unlike signs (one positive and one negative), take the difference of the absolute values of the two numbers. The sign of the answer will be the same as the sign of the number with the larger absolute value. If the absolute values of the numbers are the same, the answer is zero.

I never really liked the way these definitions were worded, but this is the mathematical way of expressing exactly how to get the answer. This is how I think about the rules.

First, I do usually rewrite each subtraction as an equivalent addition problem, unless it is two whole numbers being subtracted. In that case, if the first whole number is larger than the second whole number, I do regular whole number subtraction. If the larger whole number is being subtracted from the smaller whole number, I know the answer is negative and simply put a negative number in front of the answer.

This is how I think about adding numbers that have like signs:

• Let's say you were adding 8 + 9. These are both positive. So you just add the two whole numbers together as usual, and the answer is still positive. It's like having 8 dollars in the bank, and depositing 9 more dollars. You now have 17 dollars in the bank. So, I hope it's no surprise that 8 + 9 = 17.
• Let's say you were adding -8 + (- 9). These are both negative. This is like being in debt, and going deeper into dept. So you just add the two whole numbers together as usual, but the answer is negative. It's like owing someone 8 dollars, and then borrowing 9 more dollars. You now owe that person 17 dollars. So, -8 + (- 9) = - 17.

This is how I think about adding numbers that have unlike signs.

• Let's say you were adding 24 + (-10). Now this is an example of adding two numbers with unlike signs. Since the signs are DIFFERENT, I ignore their signs and take their DIFFERENCE – that's the same thing as just subtracting their absolute values. When I ignore their signs, I subtract the smaller number from the larger number. Then, to determine if the sign of the answer is positive or negative, I see which one outweighs the other (are there more negatives or positives?) – that's the same thing as taking the sign of the one with the absolute value. 24 + (-10) could be thought of as having 24 dollars in the bank and writing a check for 10 dollars. You still have $14 left in the bank. So, 24 + (-10) = 14.
• If you were adding -24 + 10, the problem would be done the same as the previous one except that in this case, the negatives outweigh the positives, so the final answer is negative. It's like owing someone 24 dollars and paying them 10 dollars. Now, you only owe them 14 dollars. So, -24 + 10 = -14.
• Let's say you were adding 14 + -14 or adding -83 + 83. In both of these examples, I'm adding opposites. In a way, one undoes the other. So both equal zero. This also could be done by thinking about which sign outweighs the other. But neither outweighs the other, and that is another reason the answer is neither negative nor positive, but is zero.

Using the rules at the beginning of the previous page, or the way I think about it, or maybe some other way you think about it that you are sure works and makes sense, you should be able to add and subtract integers with confidence. You should be able to explain the meaning of the operations, and be able to use manipulatives and number lines to help others learn how to add and subtract with integers and understand

Exercise 33

Perform the following arithmetic problems by first changing subtraction to adding the opposite. Then add two numbers at a time, working from left to right. Show your steps.

Exercise 34

Perform the following arithmetic problems by first changing subtraction to adding the opposite. Then add numbers with like signs together so that you have the sum of a positive and a negative number. Then add those two numbers together. Show your steps.

Remember that for a set to be closed under addition, the sum of any two elements in the set will always be in the set. For a set to be closed under subtraction, the difference of any two elements in the set will always be in the set. To prove a set is not closed under addition or subtraction, you need to provide a counterexample.

Exercise 35

For each of the following sets, determine if the set is closed under the operation given. Provide a counterexample if it is not closed

a. Integers under addition?	b. Integers under subtraction?
c. Positive integers under addition?	d. Positive integers under subtraction?
e. Negative integers under addition?	f. Negative integers under subtraction?
g. {-1, 0, 1} under addition?	h. {-1, 0, 1} under subtraction?