10.4: Decimals
- Page ID
- 83026
The meaning of decimals is best understood once one has a real understanding of place value and fractions. The decimal notation we commonly use is an extension of place value in base ten. The decimal point indicates that succeeding digits represent tenths, hundredths, thousandths, etc. So a person must understand what these fractions mean in order to understand and make the connection to decimals.
The key to understanding the relationship between decimals and fractions (or mixed numbers) begins with READING the decimal correctly. Most people read 5.3 as "five point three" which doesn't help one understand its meaning. It should be read "five and three tenths." In doing so, the connection between the decimal 5.3 and the mixed number \(5 \frac{3}{10}\) is clear. Similarly, 18.035 should be read "Eighteen and thirty-five thousandths" and corresponds to the mixed number \(18\frac{35}{1000}\). Here are a few more:
- 0.309 and \(\frac{309}{1000}\) are both correctly read "three hundred nine thousandths"
- 10.04 and \(10\frac{4}{100}\) are both correctly read "ten and four hundredths"
Note that the decimal point is read as "and". The decimal point (and the word "and") separates the whole part from the fractional part of a mixed number. This is the only correct use of the word "and" when reading numbers. 760 is read "seven hundred sixty." A common mistake is to read 760 as "seven hundred and sixty." If there is no decimal point, don't say the word "and".
People just learning about decimals (like elementary school children) should NOT read the number 5.4 as "five point four". This is a shortcut way of reading the number that is only appropriate to use once one really understands the connection between decimals and fractions. Remember that a number written in decimal form is really just a different way to write a mixed number where the denominator of the fractional part is a power of ten! The name of the fractional part (tenths, hundredths, thousandths, etc.) is the place value of the last digit of the number after the decimal point, which also happens to be the denominator of the number written in fractional form.
Look again at 0.309 and \(\frac{309}{1000}\). In the decimal, there are three digits (or place values) after the decimal point. In the fraction, there are three zeroes after the 1 (which is the number 1000 in the denominator). The same applies to 18.035 and \(18\frac{35}{1000}\). For 5.3 and \(5\frac{3}{10}\), the decimal has one digit after the decimal point, and the fraction has one zero after the 1. It's best if students are allowed to discover this fact for themselves. It's always more meaningful to discover relationships (that often become rules) on your own. Students who are regularly asked to read decimals, fractions and mixed numbers the correct way are more likely to make this particular discovery by themselves.
Mixed numbers like 5.3 and 18.035 can also be written immediately as improper fractions. The denominator of the fraction will still be the same as if it were written as a mixed number. The numerator is the number without a decimal point at all. For instance, 5.3 can be written as \(5\frac{3}{10}\) or \(\frac{53}{10}\); and 18.035 can be written as \(18\frac{35}{1000}\) or \(\frac{18035}{1000}\).
Note that when you first write a decimal as a fraction, it isn't necessarily in simplest (or reduced) form.
On the line, write in words how to read each of the following decimals. Do not use the word "point". Then, underneath, write each decimal as a fraction. If the number is greater than or equal to 1, first write the fraction as a mixed number and then write it as an improper fraction. Simplify any fraction that is not in simplest form. Show all steps (including original fractions before simplifying).
a. 0.4 _________________________________________________________________
0.4 =
b. 0.26 _________________________________________________________________
0.26 =
c. 3.08 _________________________________________________________________
3.08 =
d. 9.85 _________________________________________________________________
9.85 =
e. 17.305 _____________________________________________________________
17.305 =
Write each proper fraction as a decimal. Write each improper fraction first as a mixed number (don't reduce), and then also as a decimal. Do not use your calculator.
a. \(\frac{14}{100}\) = __________
b. \(\frac{8}{1000}\) = __________
c. \(\frac{435}{100}\) = _______________ = _______________
d. \(\frac{5638}{10}\) = _______________ = _______________
e. \(\frac{305}{100}\) = _______________ = _______________
The rule you may remember for multiplying fractions is to multiply the numbers together as if there were no decimal point, and then move the decimal point in from the right the total number of places it is in for both numbers. For instance, (8)(0.4) is done by multiplying 8 times 4 and then moving the decimal point in one place to get 3.2. Similarly, (0.06)(0.7) is done by multiplying 6 times 7 and moving the decimal point in three places (two for 0.06 and one more for 0.7 for a total of three) to get 0.042. Many people make this harder than it really is and don't realize they can easily multiply 0.3 and 0.4 in their head. It's as simple as 3 \(\cdot\) 4 and moving the decimal in two places to get 0.12. Now, how about 1.1 times 1.2? It's simply 11 times 12 with the decimal moved in two places: 1.32.
Let's observe why this rule for multiplying decimals works by rewriting the numbers as fractions first. The key here is to write numbers greater than or equal to one as improper fractions. Then multiply (without canceling or reducing) the fractions. Lastly, rewrite the fraction as a decimal.
(8)(0.4) = \(\frac{8}{1} \cdot \frac{4}{10} = \frac{32}{10}\) = 3.2 (notice the decimal point is one place in for .4)
(1.2)(1.01) = \(\frac{12}{10} \cdot \frac{101}{100} = \frac{1212}{1000}\) = 1.212
(notice the decimal point is three places in, one for 1.2 plus two more for 1.01)
Multiply the following decimals mentally, and write the answer on the blank. Then do it again by showing the same steps as shown in the previous two examples where each decimal is first written as a fraction, then multiply the numerators and denominators, and then convert that answer (don't simplify) to a decimal. Do not use your calculator.
a. (0.4)(.07) = ______________
(0.4)(.07) =
b. (1.6)(0.2) = ______________
(1.6)(0.2) =
c. (0.25)(0.3) = ______________
(0.25)(0.3) =
d. (2.2)(0.3) = ______________
(2.2)(0.3) =
Recognizing Equivalent Decimals and Comparing Decimals
Zeroes, which are behind a decimal's last non-zero digit, can be added or removed without changing the value of the decimal. If you look at some equivalent fraction, you'll see why this should be true. For example,
\[\dfrac{14}{10} = \dfrac{140}{1000} = \dfrac{1400}{10000} = \dfrac{14000}{100000}. \nonumber \]
These are all equivalent to \(\frac{14}{100}\) because the numerator and denominator was multiplied by some power of 10 (10, 100 or 1000) to get one of the other equivalent fractions. If we replace each of the four fractions above with their decimal equivalents, we get 0.14 = 0.140 = 0.1400 = 0.14000. Let's call any zeroes at the end of a decimal's last non-zero digit "trailing zeroes". Then, we could conclude that any number starting with .14 that has trailing zeroes is also equivalent, like 0.1400000.
Two decimals are equal only if one can be made to look identical to the other by adding or removing trailing zeroes. You can also determine if they are equivalent by removing any excess trailing zeroes from each to see if they are identical.
For the first decimal given, circle any of the next four decimals that are equal to it.
| a. | 1.900; | 1.0900 | 1.9 | 1.90000 | 0.190 |
| b. | 4.034; | 4.0340 | 4.0334 | 4.0034 | 4.3040 |
To compare two or more decimals that are not equal, but have the same number of digits after the decimal point, you can write each as a fraction with the same denominator and then compare the numerator. For instance 0.14 is less than 0.21 since fourteen hundredths is less than twenty-one hundredths. Basically, in this case, it's just like comparing whole numbers. You'll be able to determine which is larger by comparing each number as if there was no decimal point. But, keep in mind this only makes sense if the numbers you are looking at have the same number of digits after the decimal point.
Compare each of the following decimals using <, = or >.
| a. | 3.5 | 0.9 |
| b. | 35.06 | 35.0600 |
| c. | 0.089 | 0.098 |
To compare two or more decimals that are not equal that do not all have the same number of digits after the decimal point, first write each decimal with the same number of digits after the decimal point (by adding trailing zeroes to one or more if necessary). By doing that, you are comparing tenths with tenths, or hundredths with hundredth, etc., as you did in exercise 5.
Compare each of the following decimals using <, = or >.
| a. | 3.51 | 3.488 |
| b. | 35.061 | 35.35 |
| c. | 0.08933 | 0.0894 |
If a fraction is written with a power of ten in the denominator, it's basic to write the same number in decimal form. You did that in Exercise 2. Any fraction that is written with a power of 10 in the denominator can be written as a terminal decimal. This means that it's possible to write the number with trailing zeroes. But what if the fraction doesn't have a power of 10 (like 10, 100, 1000, etc.) in the denominator? Sometimes those can be tricky!
If a fraction WITHOUT a power of ten in the denominator CAN be written as an equivalent fraction WITH a power of ten in the denominator, then it can be written as a terminating decimal.
For instance, \(\frac{1}{2}\) can be written as \(\frac{5}{10}\) (by multiplying the numerator and denominator by 5)
Therefore, \(\frac{1}{2}\) = \(\frac{5}{10}\) = 0.5 (remember to read this as five-tenths)
Well, that one wasn't too hard, but what about \(\frac{7}{80}\)? The question is whether you can multiply the denominator, 80, by something to get 10, 100, 1000, 10000, etc. There is no whole number you can multiply 80 by to get 10, 100 or 1000. But, if you multiply 80 times 125, it equals 100000. So, by multiplying both 7 and 80 by 125, we get the equivalent fraction \(\frac{875}{10000}\) for \(\frac{7}{80}\) which can now be written as the decimal 0.0875.
How about writing \(\frac{5}{6}\) as a terminating decimal? Well, there is nothing you can multiply 6 by to get 10 or 100 or 1000 or 10000. Is there maybe some number we could multiply 6 by to get some higher power of ten? Well, that's a good question! Actually, there isn't, but how could you be sure? You certainly can't try every power of ten since there are an infinite number of them to try.
It would be nice if there was an easy way to determine if any given fraction could be written as a terminating decimal. The key is to consider the factors of the denominator of a fraction that can be written as a terminating decimal. If a fraction can be written as a terminating decimal, then there is some equivalent fraction where the denominator must be a power of ten: 10 or 100 or 1000, etc.
Write the prime factorization of each of the following:
a. 10 = _______________
b. 100 = _______________
c. 1000 = _______________
d. 10000 = _______________
e. 100000 = _______________
What are the only prime factors of powers of 10? ______________
If a power of ten has three factors of 5, how many factors of 2 does it have? ______
If a power of ten has two factors of 2, how many factors of 5 does it have? _____
Powers of ten only have 2s and 5s as its prime factors and nothing else.
Let's go back to our three numbers , \(\frac{1}{2}\), \(\frac{7}{80}\), and \(\frac{5}{6}\), that we were trying to write as terminating decimals and analyze the situation.
\(\frac{1}{2}\) is simplified, and in its prime factored form, there is exactly one 2 in the denominator. To write as an equivalent fraction with a denominator that is a power of ten, it must have only 2s and 5s as prime factors in the denominator, and the same number of each! Therefore, multiplying by one more 5 in the numerator and denominator did the trick!
Prime factor the numerator and denominator of this reduced fraction: \(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5}\)
We must determine if it is possible to multiply the denominator by something so that the resulting denominator will be made up of only 2s and 5s and the same number of each. Well, there are four factors of 2 and one factor of 5. Since we need the same number of each factor, making an equivalent fraction by multiplying the numerator and denominator by three more factors of 5 will do the trick.
\(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5} \cdot \frac{5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.0875\)
In both examples, note we either multiplied by extra factors of 2 or 5, but not both!
What about \(\frac{5}{6}\)? Well, it's reduced, and the prime factorization of the denominator is 2 \(\cdot\) 3. No matter what the denominator is multiplied by, we'll be stuck with a factor of 3 in the denominator. Since the only prime factors of powers of 10 are 2 and 5, there can't be a prime factor of 3 in the denominator if we want to end up with only a power of 10 in the denominator. Therefore, since it is impossible to write \(\frac{5}{6}\) as an equivalent fraction with a power of ten in the denominator, it cannot be written as a terminating decimal.
How about \(\frac{63}{72}\)? If we prime factor the denominator, we get 2 \(\cdot\) 2 \(\cdot\) 2 \(\cdot\) 3 \(\cdot\) 3.
Well, what do you think? Can \(\frac{63}{72}\) be written as a terminating decimal? ________
Explain why or why not.
One way to check that you are obtaining the correct results is to use a calculator. For \(\frac{1}{2}\), we got 0.5, which you can check by doing the division 1 \(\div\) 2 on your calculator.
Use your calculator to find the decimal equivalent for each of the following:
a. \(\frac{7}{80}\) = _____________
b. \(\frac{63}{72}\) = _____________
Hmmm, did you get 0.0875 for part a? _________
If you did part b on your calculator, did you get a terminating decimal of 0.875?
Is that what you expected? Why or why not?
The reason \(\frac{63}{72}\) can be written as a terminating decimal is because in its simplified form, it only has 2’s and/or 5’s as its prime factors. Here is how to finish this problem by simplifying first, and then multiplying by any needed factors of 2 or 5 to get the same number of each:
\(\frac{63}{72} = \frac{3 \cdot 3 \cdot 7}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} = \frac{7}{2 \cdot 2 \cdot 2} \cdot \frac{5\cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.875\)
For each fraction, determine if it can be written as an equivalent fraction with a power of ten in the denominator. If a fraction cannot be written as a terminal decimal, explain why not. Otherwise, show ALL of the steps (as shown in the previous examples) to write it as a terminal decimal. The steps are listed below.
- Simplify if possible
- Prime factor the denominator
- Multiply the numerator and denominator by an appropriate number of factors of 2 or 5 so that the denominator will be a power of 10
- Simplify the numerator and denominator
- Write as a terminating decimal
Then, check your answer with a calculator by taking the original fraction and dividing the numerator by the denominator. You should get the same decimal obtained by doing the five steps outlined above.
a. \(\frac{3}{4}\)
b. \(\frac{9}{20}\)
c. \(\frac{9}{15}\)
d. \(\frac{18}{25}\)
e. \(\frac{5}{14}\)
Okay, now we have to deal with those fractions that cannot be written as terminating decimals. Any simplified fraction that has at least one prime factor that isn't a 2 or 5 is in this category. Let's look at \(\frac{5}{6}\) again. One way to write this as a decimal is to divide 5 by 6.
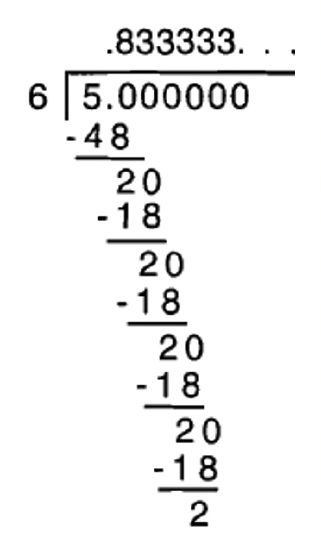
As you could see, I keep dividing 6 into 20, write 3, multiply to get 18, subtract from 20, get 2, bring down the 0, and start all over again. This can go on forever and ever. So, the 3’s at the end will trail on forever. This is NOT a terminating decimal since the number cannot be written with trailing zeroes. In this case, there are trailing 3s. The three dots at the end (called ellipses) of the number are to show that the 3s repeat forever. The answer can be written as 0.8333333... or \(0.8\bar{3}\). Remember to put the ellipses (three dots) at the end of the number! The bar over the 3 indicates that the 3 repeats forever and ever. Here are other ways to represent the same thing: \(0.8\overline{33}\) or \(0.8333\bar{3}\). In the first case, it says 33 repeats forever. In the second case, it says after the first three 3’s, the 3 repeats forever. In both cases, when you write it out in long form, it looks like 0.8333333... so it's the same number. Usually, we'll write 0.8333333... or \(0.8\bar{3}\).
Write 0.8333333... or \(0.8\bar{3}\) in three more ways, different than \(0.8\overline{33}\) or \(0.8333\bar{3}\).
____________________ , ____________________, and ____________________
One thing to notice about what happened when we divided 5 by 6 is that I kept getting 2 after each subtraction in the division, this is like the remainder. Also remember that when you divide, each remainder must be less than or equal than what you are dividing by.
Write the possible remainders for each number.
a. 6: _________________________________
b. 7: _________________________________
c. 9: _________________________________
d. 11: _________________________________
e. 3: _________________________________
Let's now look at what happens when you do long division compute \(\frac{4}{11}\) and \(\frac{2}{7}\).
 |
 |
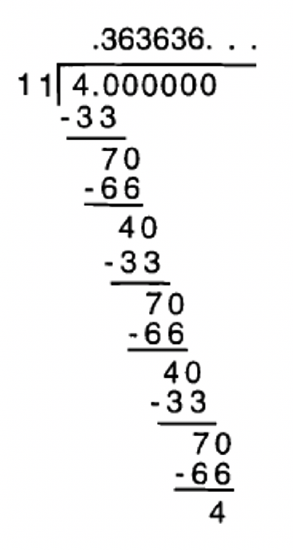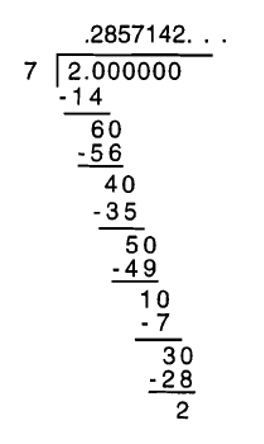In both of these cases, eventually, you get a remainder that you got previously, so the computation repeats itself. In the case of dividing 4 by 11, two remainders come up before there is some repetition 4 and 7. From 16d, you should have realized that the only possible remainders for 11 are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Now if you got a remainder of 0 when dividing, you'd have a terminating decimal. So, when dividing by 11, the most remainders you might get in a row before one repeats is 10 in a row. But in the case of \(\frac{4}{11}\), the remainders repeat after the 4 and 7. This means you keep dividing into 40 or 70 (since you bring the zero down) and that's why in the quotient the digits start repeating. Remember to put the ellipses (three dots) at the end of the number if there is a pattern of repeating digits.
Now in the case of dividing 2 by 7, the remainders you get as you go along are 6, then 4, then 5, then 1, then 3, and then 2. When you bring down the 0, you are dividing 7 into 20 again, and hence the remainders repeat. Notice that the sequence of remainders (6, 4, 5, 1, 3, and 2) is different than the sequence of digits that repeat in the quotient. The digits that repeat in the quotient are 285714, so \(\frac{2}{7}\) = 0.285714285714... or \(0.\overline{285714}\).
Since there are only six possible remainders other than zero when dividing by 7, only a sequence of 6 digits could possibly repeat. In this case, all six possible remainders of 7 appeared in the long division.
There are many ways to express the infinite or repeating decimal 0.285714285714... or \(0.\overline{285714}\). First of all, to establish what is repeating, you would want to see the sequence of digits repeating at least two times through. Therefore, 0.285714285714...is the shortest possible way of showing it when the ellipses (three dots) are used. If you simply wrote 0.285714..., it wouldn't be clear whether or not the 4 repeated or the 14 repeated, etc.
Here are a few other ways to write 0.285714285714... besides \(0.\overline{285714}\).
0.285714285714285714285714...
0.2857142857142857142...
(in this case, you see it as the 857142 repeating from this point on)
0.2857142857142857...
(in this case, you see it as the 142857 repeating from this point on)
\(0.28\overline{571428}\)
(in this case, you see it as the 571428 repeating from this point on)
Write 0.285714285714... two more ways using ellipses (the three dots) and two more ways using a bar over a repeating sequence of digits.
Determine which of the following is equivalent to 0.383432432432...
One way to do this is write the number out in long form by carefully continuing the pattern and then check the digits one place value at a time.
- 0.3834324324...
- 0.383432432...
- 0.3834323432...
- \(0.38343\overline{243}\)
- \(0.38\overline{34324}\)
Keep in mind that if you are finding a decimal equivalent for a fraction with 17 in the denominator that there may be up to sixteen digits in a row before you see any repetition. Now, obviously, there are only 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) in base ten. Note that the sequence of digits repeating in the quotient is totally different than the possible remainders you might get when you divide by 17 since a remainder may be more than a single-digit number.
a. How many possible remainders could there be if you divide a number by 33?
b. Do long division to write \(\frac{31}{33}\) as a repeating decimal using ellipses and then using the bar over the repeating digits on this line: ______________________________
Show work here:
c. In the long division, how many digits repeat? ______
d. In the long division, what were the remainders you would keep getting if you continued the division forever and ever? _________________
Use your calculator to write each as a repeating decimal. Write the answer two ways, first with a bar over the repeating digits, and then in long form, using ellipses. Note that your calculator may or may not round the last digit shown. It can't show digits repeating forever, so you have to be savvy enough to know whether the decimal showing on the display is terminal or if it is an approximation.
a. \(\frac{5}{9}\) = ________________ = _______________________________
b. \(\frac{5}{7}\) = ________________ = _______________________________
c. \(\frac{1}{6}\) = ________________ = _______________________________
d. \(\frac{2}{3}\) = ________________ = _______________________________
e. \(\frac{7}{11}\) = ________________ = _______________________________
f. \(\frac{5}{12}\) = ________________ = _______________________________
g. \(\frac{8}{15}\) = ________________ = _______________________________
h. \(\frac{16}{45}\) = ________________ = _______________________________
i. \(\frac{5}{66}\) = ________________ = _______________________________
If you are changing a simplified fraction to a decimal where the denominator is x, how many digits at most can repeat in the quotient? _________
Well, you've learned how to write terminating decimals as fractions, and how to write fractions as decimals. You should be able to determine whether a fraction can be written as a terminating or repeating decimal before doing the actual division.
Rational Numbers are defined to be numbers which can be expressed as the ratio of two integers. Fractions as we usually refer to them (without decimal points or square roots, etc. in the numerator or denominator) are rational numbers. Since all fractions can be written as terminating or nonterminating (infinite, repeating) decimals, then all terminating and repeating decimals are also rational numbers. In Exercise 1, you wrote some terminating decimals as fractions. Since all nonterminating decimals came from a fraction, now we want to be able to go the other way around and write a repeating decimal as a fraction. We've got a nifty trick for doing just that!
Let's say we wanted to write \(0.\overline{72}\) or 0.727272727272... as a fraction.
First, notice this is a very different number from 0.72, since 0.72 is seventy-two hundredths, or \(\frac{72}{100}\). This simplifies to \(\frac{18}{25}\). So,0 .72 and \(\frac{18}{25}\) are the same number. You can check to make sure \(\frac{18}{25}\) is the correct fraction by using a calculator and dividing 18 by 25. The calculator should read 0.72, which is where we started.
Okay, so how do we write \(0.\overline{72}\) as a fraction? Since this is a repeating decimal that has infinitely many digits, there is no single power of ten we can put in the denominator. The trick is to use algebra to write a number in a way that eliminates the infinitely repeating part of the decimal. First, let's write out \(0.\overline{72}\) the long way:
\(0.\overline{72}\) = .727272727272... and call it the number x. So x = 0.727272727272...
Remember that if you multiply a decimal by 10, the decimal point moves one place to the right, and when you multiply a decimal by 100, the decimal point moves two places to the right, etc.
If x = 0.727272727272..., then write out what 10x, 100x and 1000x equals. Write it out without using the bar over the repeating digits. Use the ellipses (three dots).
10x = _______________________________
100x = _______________________________
1000x = _______________________________
Okay, let's work with x = 0.727272727272... and 100x = 72.727272727272...
a. In algebra, what is 100x - x? _________ (Hint: Subtract coefficients.)
b. Compute 100x - x another way: Line up the decimal points and subtract 0.727272727272... from 72.727272727272... Notice that if the decimals are lined up, the "tails" at the end of both repeating decimals are exactly the same so it should be easy to subtract. Show the work below.
c. Write an equation so that the answer to part a equals the answer to part b. Then use algebra to solve for x. Show work.
d. Simplify the fraction you got for x in part c. Show work.
e. Use a calculator to rewrite the fraction you got in part c as a decimal:
Is it equal to \(0.\overline{72}\)? __________
If so, you must have written \(0.\overline{72}\) as the correct fraction!
Here's the trick for changing repeating decimals to simplified fractions:
Call the number you are trying to write as a decimal a variable, like \(n\) or x.
If there is one repeating digit, compute 10x; if there are two repeating digits, compute 100x; if there are three repeating digits, compute 1000x, etc. This aligns the repeating decimals up with each other so that the tail of x and the other number (10x, 100x, 1000x, etc.) is the same.
Then subtract x from the other number (10x, 100x, 1000x, etc.) The tails of both numbers will come off and you should have an algebraic problem to solve at this point. Make sure you write your answer as a reduced fraction with only integers in the numerator and denominator.
Here are two examples. If you write the number in decimal form without the bar over the number, remember to put the ellipses (three dots) at the end!
|
Write \(0.\bar{2}\) as a simplified fraction. Let x = \(0.\bar{2}\) = .222222... Since only one digit is repeating, multiply x by 10. Then 10x = 2.222222... \[\begin{aligned} 10x = & 2.22222.... \\ - x = & .2222..... \\ \hline 9x = & 2 \end{aligned} \nonumber \] \[x = \frac{2}{9}\nonumber \] Use a calculator to check that \(\frac{2}{9} = 0.\bar{2}\) |
Write \(0.\overline{54}\) as a simplified fraction. Let x = \(0.\overline{54}\) = .545454... Since two digits are repeating, multiply x by 100. Then 100x = 54.545454... \[\begin{aligned} 100x = & 54.545454... \\ - x = & .545454... \\ \hline 99x = & 54 \end{aligned} \nonumber \] \[x = \frac{54}{99} = \frac{6}{11}\nonumber \] Use a calculator to check that \(\frac{6}{11} = 0.\overline{54}\) |
Rewrite each of the following decimals as simplified fractions. For repeating decimals, use the technique shown in the previous examples. Then, check your answer using a calculator by dividing the numerator by the denominator to see if the result matches the original problem.
a. 0.4
b. \(0.\bar{4}\) Begin by letting x = \(0.\bar{4}\) or x = 0.44444...
c. 0.06 =
d. \(0.\overline{06}\) Begin by letting x = \(0.\overline{06}\) or x = 0.060606...
e. 0.9
f. \(0.\bar{9}\) Begin by letting x = \(0.\bar{9}\) or x = 0.9999... (this answer might surprise you)
g. 0.45
h. \(0.\overline{45}\) Begin by letting x = \(0.\overline{45}\) or x = 0.454545...
i. 0.084
j. \(0.\overline{084}\) Begin by letting x = \(0.\overline{084}\) or 0.084084084...
Sometimes, the arithmetic gets a little more challenging. Consider writing 0.14444... as a fraction. The 4 repeats starting two places after the decimal point. We plunge forward as before, but there's a little glitch at the end because one side of the equation will have a decimal point in it. If we were to divide by 9, the fraction will have a decimal point in the numerator so it isn't a reduced rational number; both the numerator and denominator have to be integers. Here are basic steps up until that point.
\(10n = 1.444444...\) and \(n = 0.144444\)
Subtracting, we get \(9n = 1.3\)
One way to remedy this situation is to multiply both sides of the equation by 10 (or 100 or 1000 as needed) to eliminate the decimal. This is like clearing fractions by multiplying both sides of an equation by the least common denominator.
So multiply both sides of \(9n = 1.3\) by 10 to get \(90n = 13\). Then divide by 90 to get \(\frac{13}{90}\).
Another way to remedy this situation is to write the right side of the equation as a fraction. Remember that 1.3 is \(\frac{13}{10}\). So the equation is \(9n=\frac{13}{10}\).
You can cross multiply to get \(90n = 13\) and then divide by 90 to get \(n = \frac{13}{90}\)
In any case, remember that a reduced fraction is the ratio of two integers that are relatively prime.
Rewrite each repeating decimal, use the technique shown in the previous example, as a simplified fraction. Then, using your calculator, divide the numerator by the denominator and see if the result matches the original problem.
a. 0.02828...
b. 0.2888...
c. 0.00666...
d. 0.1011011...
e. 0.3999...
So, what did you think about the answer to 24f and 25e? Both of those are little mind-boggling. It's kind of hard to accept, but 0.999999... is really the same number as 1. It's not less than 1 it's exactly 1! For 24f, if you let \(10n = 9.999...\) and \(n =0 .999...\), then subtracting \(n\) from \(10n\) yields \(9n = 9\), so \(n = 1\). That's hard to swallow, but it's the truth! Another way to see this is to realize that 1/3 + 2/3 = 1. But 1/3 = 0.333333.... and 2/3 = 0.666666... Then, 1/3 + 2/3 = 0.33333... + 0.66666... = 0.99999.... We know 1/4 + 2/3 = 1, so 0.99999... must also equal 1, as well. Oh, this stuff is just too cool!
For 0.39999..., the result of repeating 9s after a decimal makes 0.39999...= 0.4 = \(\frac{4}{10} = \frac{2}{5}\).
So, basically, any number with a bunch of trailing 9s ends up being a terminating decimal.
All of the numbers we've been dealing with so far fractions, terminating decimals, and repeating decimals make up the rational numbers. Every rational number can be written as the ratio of two relatively prime integers, and can also be written as a terminating or repeating decimal. Conversely, every terminating and repeating decimal is a rational number.
Oh, but there's more...much more!
The rationals make up a very small part of the real numbers. To complete the real number system, we have to talk about the irrational numbers. Every real number is either rational or irrational. Those numbers which cannot be written as the ratio of two relatively prime integers is irrational. Those decimal numbers which neither terminate nor repeat are irrational. So, what do they look like?
One of the most commonly known irrational numbers is \(\pi\). It is the number that is the ratio of the circumference of a circle to its diameter. Sounds like it's a ratio of two integers, but it's not! \(\pi\) can only be approximated. The most common approximation is 3.14 or 22/7. Neither of these is equal to \(\pi\) because both of these are rational numbers, and \(\pi\) is not!
Other irrational numbers are square roots of numbers that are not perfect squares, or cube roots of numbers that are not perfect cubes, etc.
For instance, these numbers are irrational: \( \sqrt{5}, \sqrt{3}, \sqrt{12}, \sqrt{20}, \sqrt[3]{35}, \sqrt[4]{72}\)
Write five irrational numbers not already listed above ________________________
Is \(\sqrt{9}\) irrational? _____ Why or why not? ________________________________
Another way to express an irrational number in decimal form is to make up a decimal that perhaps has some pattern to it, but never terminates or repeats. Two examples of this type are 2.12112111211112... and 5.010203040506070809010011012...
Write four irrational numbers in decimal form that shows a clear pattern.
Write both a rational number and an irrational number in decimal form that is between 0.53 and 0.54.
Write both a rational number and an irrational number in decimal form that is between 0.53333... and 0.54444...
Rational ______________________
Irrational ______________________
Classify each of the following numbers as rational or irrational.
a. 0.428222... ___________________
b. 0.283848... ___________________
c. \(\frac{5}{13}\) ___________________
d. \(\sqrt{80}\) ___________________
e. \(\sqrt{100}\) ___________________
f. \(\pi\) ___________________