6.7: Special Products
- Last updated
- Save as PDF
- Page ID
- 61423
This section is dedicated to explaining a number of important shortcuts for multiplying binomials. These are extremely important patterns that will produce the same products computed in previous sections. It is essential that readers practice until they become proficient using each of the patterns presented in this section.
The FOIL Method
Consider the product of two binomials \((x + 3)(x + 6)\). We already know how to find the product of these two binomials; we multiply \(x\) times both terms of \(x + 6\), then we multiply \(3\) times both terms of \(x + 6\).
\[(x+3)(x+6)=x^{2}+6 x+3 x+18 \nonumber \]
Normally we combine like terms, but we halt the process at this point so as to introduce the pattern called the FOIL method. The letters in the word FOIL stand for “First,” “Outer,” “Inner,” and “Last.”
Let’s see how we can connect these terms to the product \((x+3)(x+6)\).
- The arrows indicate the terms in the “First” positions in each binomial. If you multiply the terms in the “First” position, you get \(x^2\).\[{\color {Red}\underbrace{\color {Black}(x+3)(x}_{F}}+6) \nonumber \]
- The arrows indicate the terms in the “Outer” positions in each binomial. If you multiply the terms in the “Outer” positions, you get \(6x\).\[{\color {Red}\underbrace {\color {Black}(x+3)(x+6}_{O}}) \nonumber \]
- The arrows indicate the terms in the “Inner” positions in each binomial. If you multiply the terms in the “Inner” positions, you get \(3x\).\[(x+{\color {Red}\underbrace{\color {Black}{3)(x}}_{I}}+6) \nonumber \]
- The arrows indicate the terms in the “Last” positions in each binomial. If you multiply the terms in the “Last” positions, you get \(18\).\[(x+{\color {Red}\underbrace{\color {Black}{3)(x+6}}_{L}}) \nonumber \]
The following diagram shows the connection between “First,” “Outer,” “Inner,” “Last,” and the answer.
\[(x+3)(x+6)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ x^{2}&+&6x&+&3x&+&18\end{array} \nonumber \]
Example \(\PageIndex{1}\)
Use the FOIL method to simplify: \((x + 5)(x + 7)\)
Solution
Multiply the “First” positions: \(x^2\). Multiply the “Outer” positions: \(7x\). Multiply the “Inner” positions: \(5x\). Multiply the “Last” positions: \(35\).
\[(x+5)(x+7)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ x^{2}&+&7x&+&5x&+&35\end{array} \nonumber \]
Combining like terms, \((x+5)(x+7)=x^{2}+12 x+35\)
Exercise \(\PageIndex{1}\)
Simplify: \((x + 2)(x + 11)\)
- Answer
-
\(x^{2}+13 x+22\)
Example \(\PageIndex{2}\)
Use the FOIL method to simplify: \((2x−7)(x−4)\)
Solution
Multiply the “First” positions: \(2x^2\). Multiply the “Outer” positions: \(−8x\). Multiply the “Inner” positions: \(−7x\). Multiply the “Last” positions: \(28\).
\[(2x-7)(x-4)=\begin{array}{ccccccc} \color {Red}{F} & {} & \color {Red}{O} & {} & \color {Red}{I} & {} & \color {Red}{L}\\ 2x^{2}&-&8x&-&7x&+&28\end{array} \nonumber \]
Combining like terms, \((2 x-7)(x-4)=2 x^{2}-15 x+28\)
Exercise \(\PageIndex{2}\)
Simplify: \((x−1)(4x + 5)\)
- Answer
-
\(4 x^{2}+x-5\)
At first glance, the FOIL method doesn’t look like much of a shortcut. After all, if we simply use the distributive property on the product of Example \(\PageIndex{2}\), we get the same quick result.
\[\begin{aligned}(2 x-7)(x-4) &=2 x(x-4)-7(x-4) \\ &=2 x^{2}-8 x-7 x+28 \\ &=2 x^{2}-15 x+28 \end{aligned} \nonumber \]
The FOIL method becomes a true shortcut when we add the “Outer” and “Inner” results in our head.
FOIL Shortcut
To multiply two binomials, follow these steps:
- Multiply the terms in the “First” positions.
- Multiply the terms in the “Outer” and “Inner” positions and combine the results mentally (if they are like terms).
- Multiply the terms in the “Last” positions.
Example \(\PageIndex{3}\)
Use the FOIL shortcut to simplify: \((3x + 8)(2x−1)\)
Solution
Each of the following steps is performed mentally.
- Multiply the terms in the “First” positions: \(6x^2\)
- Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(−3x + 16x = 13x\)
- Multiply the terms in the “Last” positions: \(−8\)
Write the answer with no intermediate steps: \((3 x+8)(2 x-1)=6 x^{2}+13 x-8\)
Exercise \(\PageIndex{3}\)
Simplify: \((2z−3)(5z−1)\)
- Answer
-
\(10 z^{2}-17 z+3\)
Example \(\PageIndex{4}\)
Use the FOIL shortcut to simplify: \((4y−3)(5y + 2)\)
Solution
Each of the following steps is performed mentally.
- Multiply the terms in the “First” positions: \(20y^2\)
- Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(8y−15y = −7y\)
- Multiply the terms in the “Last” positions: \(−6\)
Write the answer with no intermediate steps: \((4 y-3)(5 y+2)=20 y^{2}-7 y-6\)
Exercise \(\PageIndex{4}\)
Simplify: \((7 x+2)(2 x-3)\)
- Answer
-
\(14 x^{2}-17 x-6\)
The Difference of Squares
We can use the FOIL shortcut to multiply \((a + b)(a−b)\).
- Multiply the terms in the “First” positions: \(a^2\)
- Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(ab−ab =0\)
- Multiply the terms in the “Last” positions: \(−b^2\)
Thus, \((a+b)(a-b)=a^{2}-b^{2}\). Note how the right-hand side \(a^2 −b^2\) is the difference of two squares. This leads to the following shortcut.
The difference of squares
If you have identical terms in the “First” positions and identical terms in the “Last” positions, but one set is separated with a plus sign while the other is separated by a minus sign, then proceed as follows:
- Square the “First” term.
- Square the “Last” term.
- Place a minus sign between the results
That is,
\[(a+b)(a-b)=a^{2}-b^{2} \nonumber \]
Note
If you don’t have identical terms in the “First” and “Last” positions, with one set separated with a plus sign and the other with a minus sign, then you do not have the difference of squares pattern and you must find some other way to multiply. For example, \((x+3)(x−3)\) is an example of the difference of squares pattern, but \((2y + 3)(2y−5)\) is not.
Example \(\PageIndex{5}\)
Use the difference of squares shortcut to simplify: \((x+3)(x− 3)\)
Solution
Note how the terms in the “First” position are identical, as are the terms in the “Last” position, with one set separated by a plus sign and the other with a minus sign. Hence, this is the difference of squares pattern and we proceed as follows:
- Square the term in the “First” position: \(x^2\)
- Square the term in the “Last” position: \((−3)^2 =9\)
- Separate the squares with a minus sign.
That is:
\[\begin{aligned}(x+3)(x-3) &=x^{2}-(3)^{2} \\ &=x^{2}-9 \end{aligned} \nonumber \]
Note
You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((x + 3)(x−3) = x^2 −9\).
Exercise \(\PageIndex{5}\)
Simplify: \((x + 5)(x−5)\)
- Answer
-
\(x^{2}-25\)
Example \(\PageIndex{6}\)
Use the difference of squares shortcut to simplify: \((8y +7z)(8y−7z)\)
Solution
Note how the terms in the “First” position are identical, as are the terms in the “Last” position, with one set separated by a plus sign and the other with a minus sign. Hence, this is the difference of squares pattern and we proceed as follows:
- Square the term in the “First” position: \((8y)^2 = 64 y^2\)
- Square the term in the “Last” position: \((7z)^2 = 49 z^2\)
- Separate the squares with a minus sign.
That is:
\[\begin{aligned}(8 y+7 z)(8 y-7 z) &=(8 y)^{2}-(7 z)^{2} \\ &=64 y^{2}-49 z^{2} \end{aligned} \nonumber \]
Note
You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((8 y+7 z)(8 y-7 z)=64 y^{2}-49 z^{2}\)
Exercise \(\PageIndex{6}\)
Simplify: \((3a−6b)(3a +6b)\)
- Answer
-
\(9 a^{2}-36 b^{2}\)
Example \(\PageIndex{7}\)
Use the difference of squares shortcut to simplify: \(\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right)\)
Solution
Note how the terms in the “First” position are identical, as are the terms in the “Last” position, with one set separated by a plus sign and the other with a minus sign. Hence, this is the difference of squares pattern and we proceed as follows:
- Square the term in the “First” position: \((x^3)^2 = x^6\)
- Square the term in the “Last” position: \((5y^2)^2 = 25 y^4\)
- Separate the squares with a minus sign.
That is:
\[\begin{aligned}\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right) &=\left(x^{3}\right)^{2}-\left(5 y^{2}\right)^{2} \\ &=x^{6}-25 y^{4} \end{aligned} \nonumber \]
Note
You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \(\left(x^{3}-5 y^{2}\right)\left(x^{3}+5 y^{2}\right)=x^{6}-25 y^{4}\)
Exercise \(\PageIndex{7}\)
Simplify: \(\left(2 y^{4}+z^{3}\right)\left(2 y^{4}-z^{3}\right)\)
- Answer
-
\(4 y^{8}-z^{6}\)
Squaring a Binomial
Before demonstrating the correct procedure for squaring a binomial, we will first share one of the most common mistakes made in algebra.
Warning! This is incorrect!
One of the most common mistakes made in algebra is the assumption that:
\[(a+b)^{2}=a^{2}+b^{2} \nonumber \]
The fact that this is incorrect is easily checked. Substitute \(3\) for \(a\) and \(4\) for \(b\).
\[\begin{aligned}(3+4)^{2} &=3^{2}+4^{2} \\ 7^{2} &=3^{2}+4^{2} \\ 49 &=9+16 \end{aligned} \nonumber \]
Clearly this is incorrect!
So what is the correct answer? First, \((a+b)^{2}=(a+b)(a+b)\). We can now use the FOIL shortcut.
- Multiply the terms in the “First” positions: \(a^2\)
- Multiply the terms in the “Outer” and “Inner” positions and add the results mentally: \(ab + ab =2ab\)
- Multiply the terms in the “Last” positions: \(b^2\)
Hence, the correct answer is \((a+b)^{2}=a^{2}+2 a b+b^{2}\). This leads us to the following shortcut for squaring a binomial.
Squaring a binomial
To square a binomial, such as \((a + b)^2\), perform the following steps:
- Square the “First” term: \(a^2\)
- Multiply the “First” and “Last” terms and double the result: \(2ab\)
- Square the “Last” term: \(b^2\)
That is:
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber \]
Example \(\PageIndex{8}\)
Use the squaring a binomial shortcut to expand: \((x+5)^{2}\)
Solution
Follow these steps:
- Square the first term: \(x^2\)
- Multiply the “First” and “Last” terms and double the result: \(2(x)(5) = 10x\)
- Square the “Last” term: \(5^2 = 25\)
Thus:
\[\begin{aligned}(x+5)^{2} &=x^{2}+2(x)(5)+(5)^{2} \\ &=x^{2}+10 x+25 \end{aligned} \nonumber \]
Note
You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((x+5)^{2}=x^{2}+10 x+25\)
Exercise \(\PageIndex{8}\)
Simplify: \((x+3)^{2}\)
- Answer
-
\(x^{2}+6 x+9\)
Comment
Students often refuse to learn the “squaring a binomial” shortcut, noting that they can just as easily use the FOIL technique or a simple application of the distributive property to arrive at the same result. Unfortunately, failure to learn the “squaring a binomial” shortcut will severely handicap students, as this pattern is an important component of many procedures in future mathematics courses.
Example \(\PageIndex{9}\)
Use the squaring a binomial shortcut to expand: \((3 x+7 y)^{2}\)
Solution
Follow these steps:
- Square the first term: \((3x)^2 =9x^2\)
- Multiply the “First” and “Last” terms and double the result: \(2(3x)(7y)= 42xy\)
- Square the “Last” term: \((7y)^2 = 49 y^2\)
Thus:
\[\begin{aligned}(3 x+7 y)^{2} &=(3 x)^{2}+2(3 x)(7 y)+(7 y)^{2} \\ &=9 x^{2}+42 x y+49 y^{2} \end{aligned} \nonumber \]
Note
You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \((3 x+7 y)^{2}=9 x^{2}+42 x y+49 y^{2}\)
Exercise \(\PageIndex{9}\)
Simplify: \((2 y+3 z)^{2}\)
- Answer
-
\(4 y^{2}+12 y z+9 z^{2}\)
In the next example, when squaring a binomial with a minus sign, we take care of the minus sign by “adding the opposite.”
Example \(\PageIndex{10}\)
Use the squaring a binomial shortcut to expand: \(\left(4 a^{2}-5 b^{3}\right)^{2}\)
Solution
Add the opposite: \((4a^2−5b^3)^2 = (4 a^2+(−5b^3))^2\). Now follow these steps:
- Square the first term: \((4a^2)^2 = 16 a^4\)
- Multiply the “First” and “Last” terms and double the result: \(2(4a^2)(−5b^3)= −40a^2b^3\)
- Square the “Last” term: \((−5b^3)^2 = 25 b^6\)
Thus:
\[\begin{aligned}\left(4 a^{2}-5 b^{3}\right)^{2} &=\left(4 a^{2}+\left(-5 b^{3}\right)\right)^{2} \\ &=\left(4 a^{2}\right)^{2}+2\left(4 a^{2}\right)\left(-5 b^{3}\right)+\left(-5 b^{3}\right)^{2} \\ &=16 a^{4}-40 a^{2} b^{3}+25 b^{6} \end{aligned} \nonumber \]
Note
You should practice this pattern until you can go straight from the problem statement to the answer without writing down any intermediate work, as in \[\left(4 a^{2}-5 b^{3}\right)^{2}=16 a^{4}-40 a^{2} b^{3}+25 b^{6} \nonumber \]
Exercise \(\PageIndex{10}\)
Simplify: \(\left(3 x^{4}-5 z^{2}\right)^{2}\)
- Answer
-
\(9 x^{8}-30 x^{4} z^{2}+25 z^{4}\)
Example \(\PageIndex{10}\) shows us that if we are squaring a difference, the middle term will be minus. That is, the only difference between \((a+b)^2\) and \((a−b)^2\) is the sign of the middle term.
Squaring a binomial
The shortcuts for squaring a binomial are:
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \nonumber \]
\[(a-b)^{2}=a^{2}-2 a b+b^{2} \nonumber \]
Example \(\PageIndex{11}\)
Use the squaring a binomial shortcut to expand: \(\left(x^{3}-y^{3}\right)^{2}\)
Solution
Use the pattern \((a−b)^2 = a^2 −2ab+ b^2\). Square the “First” term, multiply the “First” and “Last” terms and double the result, then square the “Last” term. Because of the minus sign, the middle term will be minus, but all other terms are plus.
\[\begin{aligned}\left(x^{3}-y^{3}\right)^{2} &=\left(x^{3}\right)^{2}-2\left(x^{3}\right)\left(y^{3}\right)+\left(y^{3}\right)^{2} \\ &=x^{6}-2 x^{3} y^{3}+y^{6} \end{aligned} \nonumber \]
Exercise \(\PageIndex{11}\)
Simplify: \(\left(a^{2}-3 b^{5}\right)^{2}\)
- Answer
-
\(a^{4}-6 a^{2} b^{5}+9 b^{10}\)
An Application
In Example \(\PageIndex{7}\), we found the area of the outer square by summing the areas of its parts (see Figure \(\PageIndex{1}\)). Recall that the answer was \(A = x^2 + 6x + 9\).
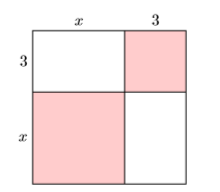
Now that we have the squaring a binomial shortcut, we can simplify the process of finding the area of the outer square by squaring its side. That is:
\[A=(x+3)^{2} \nonumber \]
Now we can use the squaring the binomial technique to expand.
\[\begin{array}{l}{=x^{2}+2(x)(3)+(3)^{2}} \\ {=x^{2}+6 x+9}\end{array} \nonumber \]
Note that this is the same as the answer found by summing the four parts of the square in Example \(\PageIndex{7}\).


