2.8: Solving Polynomial Equations

We begin by introducing a property that will be used extensively in this and future sections.

The Zero Factor Property

If the product of two or more numbers equals zero, then at least one of the numbers must equal zero. That is, if

\(ab =0\)

then

\(a = 0\) or \(b =0\)

Let’s use the zero factor property to solve a few equations.

Example \(\PageIndex{1}\)

Solve for \(x\): \((x+3)(x-5)=0\)

Solution

The product of two factors equals zero.

\[(x+3)(x-5)=0 \nonumber \]

Hence, at least one of the factors must equal zero. Using the zero product property, set each factor equal to zero, then solve the resulting equations for \(x\).

\[\begin{aligned} x+3 &=0 \\ x &=-3 \end{aligned} \nonumber \]

or

\[\begin{aligned} x-5 &=0 \\ x &=5 \end{aligned} \nonumber \]

Hence, the solutions are \(x = −3\) and \(x =5\)

Check:

Check that each solution satisfies the original equation.

Substitute \(−3\) for \(x\):

\[\begin{aligned}(x+3)(x-5) &=0 \\(-3+3)(-3-5) &=0 \\(0)(-8) &=0 \\ 0 &=0 \end{aligned} \nonumber \]

Substitute \(5\) for \(x\):

\[\begin{aligned}(x+3)(x-5) &=0 \\(5+3)(5-5) &=0 \\(8)(0) &=0 \\ 0 &=0 \end{aligned} \nonumber \]

Because each check produces a true statement, both \(x = −3\) and \(x = 5\) are solutions of \((x + 3)(x−5) = 0\).

You Try \(\PageIndex{1}\)

Solve for x: \((x-7)(x-2)=0\)

Answer

\(7\), \(2\)

The zero product property also works equally well if more than two factors are present. For example, if \(abc = 0\), then either \(a = 0\) or \(b = 0\) or \(c = 0\). Let’s use this idea in the next example.

Example \(\PageIndex{2}\)

Solve for \(x\): \(x(2x + 9)(3x−5) = 0\)

Solution

The product of three factors equals zero.

\[x(2x + 9)(3x−5) = 0 \nonumber \]

Using the zero product property, set each factor equal to zero, then solve the resulting equations for \(x\).

\[x=0 \nonumber \]

or

\[\begin{align*} 2x + 9 &= 0\\ 2x &= -9\\ x &= -\dfrac{9}{2} \end{align*} \nonumber \]

or

\[\begin{align*} 3x - 5 &= 0\\ 3x &= 5\\ x &= \dfrac{5}{3} \end{align*} \nonumber \]

Hence, the solutions are \(x = 0\), \(x = −9/2\), and \(x =5 /3\). We encourage the reader to check the solution.

You Try \(\PageIndex{2}\)

Solve for \(x\): \(6x(x + 4)(5x + 1) = 0\)

Answer

\(0\), \(−4\), \(−1/5\)

Linear versus Nonlinear Equations

Many equations that you have solved in the past were linear equations. Linear equations contain terms where the highest power of the variable we are solving for is one. Nonlinear equations have a power on the variable we are solving for that exceeds one. In this chapter we are learning how to solve nonlinear equations involving polynomials. L'ets briefly make sure we can recognize the difference between a linear and a nonlinear equation.

Linear versus Nonlinear Equations

Use the following conditions to determine if an equation is linear or nonlinear.

1. If the highest power of the variable we are solving for is one, then the equation is linear.
2. If the highest power of the variable we are solving for is larger than one, then the equation is nonlinear.

Example \(\PageIndex{3}\)

If the instruction is “solve for \(x\),” classify each of the following equations as linear or nonlinear.

1. \(3x−5=4−7x\)
2. \(x^2 =8x\)

Solution

Because the instruction is “solve for \(x\),” to determine whether the equation is linear or nonlinear, we identify the largest power of \(x\) present in the equation.

1. The highest power of \(x\) present in the equation \(3x− 5=4− 7x\) is one. Hence, this equation is linear.
2. The equation \(x^2 =8 x\) contains a power of \(x\) higher than one (it contains an \(x^2\)). Hence, this equation is nonlinear.

Example \(\PageIndex{4}\)

Solve: \(3 x−5=4−7x\)

Solution

Note that the largest power of the variable in the equation,\(x\), is one so the equation \(3x−5=4−7x\) is linear. Hence, the strategy is to move all terms containing the variable, \(x\), to one side of the equation, then move all the remaining terms to the other side of the equation.

\[\begin{array}{rlrl}{3 x-5} & {=4-7 x} & {\color {Red} \text { Original equation. }} \\ {3 x-5+7 x} & {=4} & {\color {Red} \text { Add } 7 x \text { to both sides. }} \\ {3 x+7 x} & {=4+5} & {\color {Red} \text { Add } 5 \text { to both sides. }}\end{array} \nonumber \]

Note how we have succeeded in moving all terms containing \(x\) to one side of the equation and all terms that do not contain \(x\) to the other side of the equation.

\[\begin{array}{rlrl}{10 x} & {=9} & {} & {\color {Red} \text { Simplify both sides. }} \\ {x} & {=\dfrac{9}{10}} & {} & {\color {Red} \text { Divide both sides by } 10 .}\end{array} \nonumber \]

Hence, the solution of \(3x−5=4−7x\) is \(x =9 /10\). Readers are encouraged to check this solution.

The situation is much different when the equation is nonlinear.

Strategy for Solving a Nonlinear Equation

If an equation is nonlinear, first move everything to one side of the equation, making one side of the equation equal to zero. Continue the solution process by factoring and applying the zero factor property.

Example \(\PageIndex{5}\)

Solve: \(x^2 = 8x\)

Solution

Because the instruction is “solve for \(x\),” and the highest power of \(x\) is larger than one, the equation \(x^2 =8x\) is nonlinear. Hence, the strategy requires that we move all terms to one side of the equation, making one side zero.

\[\begin{array}{rlrl}{x^{2}} & {=8 x} \quad {\color {Red} \text { Original equation. }} \\ {x^{2}-8 x} & {=0} \quad {\color {Red} \text { Get zero on one side. }}\end{array} \nonumber \]

Next, we factor out the \(\mathrm{GCF}\) on the left-hand side.

\[x(x-8) = 0 \quad \color {Red} \text {Factor out the GCF.} \nonumber \]

By the zero factor property, either the first factor is zero or the second factor is zero.

\[\begin{array}{r}{x=0 \quad \text { or } \quad x-8=0} \\ {x=8}\end{array} \nonumber \]

Hence, the solutions are \(x = 0\) and \(x = 8\).

Check:

Check that each solution satisfies the original equation.

\[\begin{array}{l}{\text { Substitute } 0 \text { for } x :} \\ {\qquad \begin{aligned} x^{2} &=8 x \\(0)^{2} &=8(0) \\ 0 &=0 \end{aligned}}\end{array} \nonumber \]

\[\begin{array}{l}{\text { Subtitute } 8 \text { for } x :} \\ {\qquad \begin{aligned} x^{2} &=8 x \\(8)^{2} &=8(8) \\ 64 &=64 \end{aligned}}\end{array} \nonumber\]

Note that both results are true statements, guaranteeing that both \(x = 0\) and \(x = 8\) are solutions of \(x^2 =8x\)

You Try \(\PageIndex{5}\)

Solve: \(t^2 =−5t\)

Answer

\(0\), \(-5\)

Caution!

Consider what would happen if we divided both sides of the equation \(x^2 =8x\) in Example \(\PageIndex{5}\) by \(x\):

\[\begin{aligned} x^{2} &=8 x \\ \dfrac{x^{2}}{x} &=\dfrac{8 x}{x} \\ x &=8 \end{aligned} \nonumber \]

We have lost one of the answers found in Example \(\PageIndex{5}\), \(x = 0\).

You should never divide by the variable you are solving for because you could be dividing by zero which is not mathematically possible. You also will lose answers to your equation.

Let’s try solving a nonlinear equation that requires factoring by grouping.

Example \(\PageIndex{6}\)

Solve: \(6x^2 +9x−8x−12 = 0\)

Solution

This equation is nonlinear. Begin by moving everything to one side of the equation, making one side equal to zero. Then factor.

Since zero is one side already, let’s factor the left-hand side by grouping since there are four terms,

\[\begin{align*} 6x^2+9x-8x-12 &=0 \\ (6x^2+9x)-(8x+12)&=0\\ 3x {\color{Red}(2x+3)}-4 {\color{Red}(2x+3)}&=0\\ (3x-4){\color {Red}(2x + 3)}&=0 \end{align*}\]

We now have a product of two factors that equals zero. Use the zero product property to write:

\[\begin{aligned} 3x-4 &=0 \\ 3x &= 4 \\ x &=\dfrac{4}{3} \end{aligned} \nonumber \]

or

\[\begin{aligned} 2x+3 &=0 \\ 2x &= -3 \\ x &= -\dfrac{3}{2} \end{aligned}\]

Hence, the solutions are \(x =4 /3\) and \(x =−3/2\). We leave it to the reader to check that the solutions in the original equation.

You Try \(\PageIndex{6}\)

Solve: \(5w^2 −20w−4w + 16 = 0\)

Answer

\(4/5\), \(4\)

Using the Graphing Calculator

In this section we will employ two different calculator routines to find the solution of a nonlinear equation. Before picking up the calculator, let’s first use an algebraic method to solve the equation \(x^2 = −5x\). The equation is nonlinear, so the first step is to move everything to one side of the equation, making one side equal to zero.

\[\begin{aligned} x^{2} &= -5x \quad \color {Red} \text { Nonlinear. Make one side zero. } \\ x^{2}+5 x &= 0 \quad \color {Red} \text { Add } 5x \text { to both sides. } \\ x(x+5) &= 0 \quad \color {Red} \text { Factor out the GCF. } \end{aligned} \nonumber \]

Use the zero product property, setting each factor equal to zero, then solving the resulting equations for \(x\).

\[x=0 \nonumber \]

or

\[\begin{aligned} x+5&=0 \\ x&=-5 \end{aligned} \nonumber \]

Hence, the solutions are \(x = 0\) and \(x = −5\).

We’ll now use the calculator to find the solutions of \(x^2 = −5x\). The first technique employs the 5:intersect routine on the calculator’s CALC menu.

Example \(\PageIndex{7}\)

Use the 5:intersect utility on the graphing calculator to solve the equation \(x^2 = −5x\) for \(x\).

Solution

Load the left-hand side of \(x^2 = −5x\) in \(\mathbb{Y1}\) and the right-hand side in \(\mathbb{Y2}\) (see Figure \(\PageIndex{1}\)). Selecting 6:ZStandard from the ZOOM menu produces the graphs shown in the image on the right in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Graphs of each side of the equation \(x^2 = −5x\).

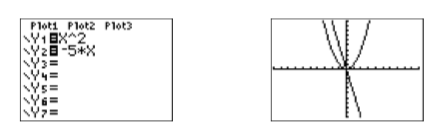
Note that the graph of \(y = x^2\) is a parabola that opens upward, with vertex (turning point) at the origin. This graph reveals why the equation \(x^2 = −5x\) is called a nonlinear equation (not all the graphs involved are lines). Next, the graph of \(y = −5x\) is a line with slope \(−5\) and \(y\)-intercept at the origin.

The two graphs obviously intersect at the origin, but it also appears that there may be another point of intersection that is off the screen. Let’s increase \(\mathbb{Ymax}\) in an attempt to reveal the second point of intersection. After some experimentation, the settings shown in the first image in Figure \(\PageIndex{2}\) reveal both points of intersection. Pushing the GRAPH button produces the image on the right in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): WINDOW parameters settings to reveal both points of intersection.

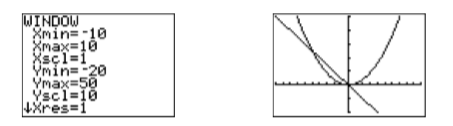
To find the solutions of the equation \(x^2 =−5x\), we must find the coordinates of the points where the graphs of \(y = x^2\) and \(y = −5x\) intersect. The \(x\)-coordinate of each point of intersection will be a solution of the equation \(x^2 = −5x\).

• Start by selecting 5:intersect from the CALC menu. When prompted for the “First curve?”, press ENTER. When prompted for the “Second curve?”, press ENTER. When prompted for a “Guess,” press ENTER. The result is the point \((0,0)\) shown in the image on the left in Figure \(\PageIndex{3}\).
• Repeat the process a second time. Select 5:intersect from the CALC menu. When prompted for the “First curve?”, press ENTER. When prompted for the “Second curve?”, press ENTER. When prompted for a “Guess,” use the left-arrow key to move the cursor closer to the leftmost point of intersection, then press ENTER. The result is the point \((−5,25)\) shown in the image on the right in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): Graphs showing using the 5:intersect utility to find the points of intersection.

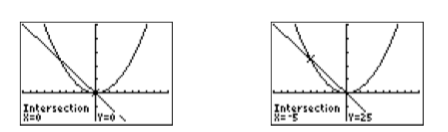
Hence, the solutions of \(x^2 = −5x\) are \(x = −5\) and \(x = 0\).

You Try \(\PageIndex{7}\)

Use the 5:intersect utility on the graphing calculator to solve the equation \(x^2 =4x\) for \(x\).

Answer

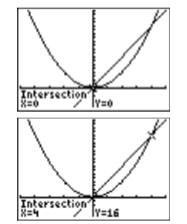
Before demonstrating a second graphing calculator technique for solving nonlinear equations, let’s take a moment to metnion the relationship between zeros and x-intercepts.

Zeros and \(x\)-intercepts

The points where the graph of \(f\) crosses the \(x\)-axis are called the \(x\)-intercepts of the graph of \(f\). The \(x\)-value of each \(x\)-intercept is called a zero of the function \(f\).

We recently solved the equation \(x^2 = −5x\) by using the 5:intersect feature on the graphing calculator. We’ll now employ the 2:zero utility from the CALC menu to find the solutions of the equation \(x^2 = −5x\).

Example \(\PageIndex{8}\)

Use the 2:zero utility on the graphing calculator to solve the equation \(x^2 = −5x\) for \(x\).

Solution

First, make one side of the equation equal to zero.

\[\begin{aligned}x^{2} &=-5 x \quad \color {Red} \text { Make one side zero. } \\ x^{2}+5 x &=0 \quad \color {Red} \text { Add } 5 x \text { to both sides. }\end{aligned} \nonumber \]

To determine the values of \(x\) that make \(x^2 +5x = 0\), we must locate the points where the graph of \(f(x)=x^2 +5x\) crosses the \(x\)-axis. These points are the \(x\)-intercepts of the graph of \(f\) and the \(x\)-values of these points are the zeros of the function \(f\).

Load the function \(f(x)=x^2 +5 x\) in \(\mathbb{Y1}\), then select 6:ZStandard to produce the image in Figure \(\PageIndex{4}\). Note that the graph of \(f\) has two \(x\)-intercepts, and the \(x\)-values of each of these points are the zeros of the function \(f\).

Figure \(\PageIndex{4}\): Graph of \(p(x)=x^2 +5x\).

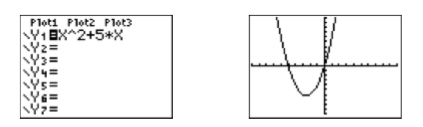
Select 2:zero from the CALC menu (see Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): Visuals of calculator screen showing the 2:zero feature to find the \(x\)-intercepts of the graph of \(f(x)=x^2 +5x\).

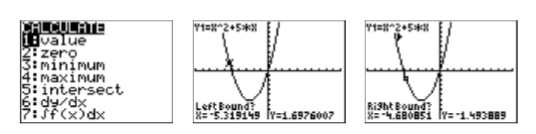
• The calculator responds by asking for a “Left Bound?” Use the left-arrow key to move the cursor so that it lies to the left of the \(x\)-intercept near \((−5,0)\) (see the second image in Figure \(\PageIndex{5}\)), then press the ENTER key.
• The calculator responds by asking for a “Right Bound?” Move the cursor so that is slightly to the right of the x-intercept near \((−5,0)\) (see the third image Figure \(\PageIndex{6}\)), then press the ENTER key.
• The calculator responds by asking for a “Guess?” Note the two triangular marks near the top of the viewing window in the first image in Figure \(\PageIndex{6}\) that mark the left- and right-bounds. As long as you place the cursor so that the x-value of the cursor location lies between these two marks, you’ve made a valid guess. Because the cursor already lies between these two marks, we usually leave it where it is and press the ENTER key.

Figure \(\PageIndex{6}\): Visuals of calculator screen showing the 2:zero feature to find the \(x\)-intercepts of the graph of \(f(x)=x^2 +5x\).

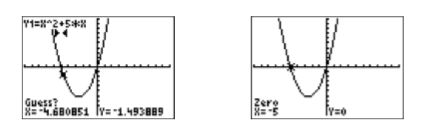
After making your guess and pressing the ENTER key, the calculator proceeds to find an approximation of the \(x\)-intercept that lies between the left- and right-bounds previously marked (see the second image in Figure \(\PageIndex{6}\). Hence, this \(x\)-intercept is \((−5,0)\), making \(−5\) a zero of \(f(x)=x^2 +5x\) and a solution of the equation \(x^2 +5x = 0\).

We’ll leave it to our readers to repeat the 2:zero process to find the second zero at the origin.

Hence, the solutions of \(x^2 = −5x\) are \(x = −5\) and \(x = 0\).

Note

It’s often easier to find the solutions of a nonlinear equation by making one side zero and identifying where the graph of the resulting function crosses the \(x\)-axis.