2.23: Complex Numbers

Evaluating the Square Root of a Negative Number

Whenever we have a situation where we have a square root of a negative number we say there is no real number that equals that square root. For example, to simplify $\sqrt{-1}$, we are looking for a real number $x$ so that $x^{2}=-1$. Since all real numbers squared are positive numbers, there is no real number that equals $–1$ when squared.

Mathematicians have often expanded their numbers systems as needed. They added $0$ to the counting numbers to get the whole numbers. When they needed negative balances, they added negative numbers to get the integers. When they needed the idea of parts of a whole they added fractions and got the rational numbers. Adding the irrational numbers allowed numbers like $\sqrt{5}$. All of these together gave us the real numbers and so far in your study of mathematics, that has been sufficient.

But now we will expand the real numbers to include the square roots of negative numbers. We start by defining the imaginary unit $i$ as the number whose square is $–1$.

Imaginary Unit

The imaginary unit $i$ is the number whose square is $-1$.

$i^{2}=-1 \text { or } i=\sqrt{-1}$

We will use the imaginary unit to simplify the square roots of negative numbers.

Square Root of a Negative Number

If $b$ is a positive real number, then

$\sqrt{-b}=\sqrt{b} i$

We will use this definition in the next example. Be careful that it is clear that the $i$ is not under the radical. Sometimes you will see this written as $\sqrt{-b}=i \sqrt{b}$ to emphasize the $i$ is not under the radical. But the $\sqrt{-b}=\sqrt{b} i$ is considered standard form.

Example $\PageIndex{1}$

Write each expression in terms of $i$ and simplify is possible:

1. $\sqrt{-25}$
2. $\sqrt{-7}$
3. $\sqrt{-12}$

Solution:

a.

$\sqrt{-25}$

Use the definition of the square root of negative numbers.

$\sqrt{25} i$

Simplify.

$5i$

b.

$\sqrt{-7}$

Use the definition of the square root of negative numbers.

$\sqrt{7} i$

Simplify.

Be careful that it is clear that $i$ is not under the radical sign.

c.

$\sqrt{-12}$

Use the definition of the square root of negative numbers.

$\sqrt{12} i$

Simplify $\sqrt{12}$.

$2 \sqrt{3} i$

You Try $\PageIndex{1}$

Write each expression in terms of $i$ and simplify if possible:

1. $\sqrt{-81}$
2. $\sqrt{-5}$
3. $\sqrt{-18}$

Answer

1. $9i$
2. $\sqrt{5} i$
3. $3 \sqrt{2} i$

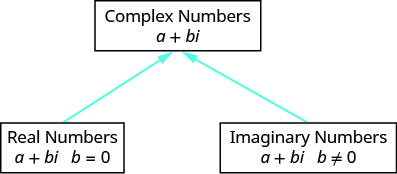
Now that we are familiar with the imaginary number $i$, we can expand the real numbers to include imaginary numbers. The complex number system includes the real numbers and the imaginary numbers. A complex number is of the form $a+bi$, where $a, b$ are real numbers. We call $a$ the real part and $b$ the imaginary part.

Complex Number

A complex number is of the form $a+bi$, where $a$ and $b$ are real numbers.

Figure $\PageIndex{1}$

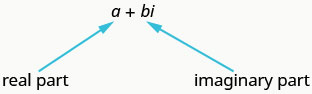
A complex number is in standard form when written as $a+bi$, where $a$ and $b$ are real numbers.

If $b=0$, then $a+bi$ becomes $a+0⋅i=a$, and is a real number.

If $b≠0$, then $a+bi$ is an imaginary number.

If $a=0$, then $a+bi$ becomes $0+bi=bi$, and is called a pure imaginary number.

We summarize this here.

Table 8.8.1

	$a+bi$
$b=0$	$a+0 \cdot i$ $a$	Real number
$b\neq 0$	$a+bi$	Imaginary number
$a=0$R	$0+bi$ $bi$	Pure imaginary numbe4

The standard form of a complex number is $a+bi$, so this explains why the preferred form is $\sqrt{-b}=\sqrt{b} i$ when $b>0$.

The diagram helps us visualize the complex number system. It is made up of both the real numbers and the imaginary numbers.

Figure $\PageIndex{2}$

Adding and Subtracting Complex Numbers

We are now ready to perform the operations of addition, subtraction, multiplication and division on the complex numbers—just as we did with the real numbers.

Adding and subtracting complex numbers is much like adding or subtracting like terms. We add or subtract the real parts and then add or subtract the imaginary parts. Our final result should be in standard form.

Example $\PageIndex{2}$

Add: $\sqrt{-12}+\sqrt{-27}$

Solution:

$\sqrt{-12}+\sqrt{-27}$

Use the definition of the square root of negative numbers.

$\sqrt{12} i+\sqrt{27} i$

Simplify the square roots.

$2 \sqrt{3} i+3 \sqrt{3} i$

Add.

$5 \sqrt{3} i$

You Try $\PageIndex{2}$

Add: $\sqrt{-8}+\sqrt{-32}$

Answer

$6 \sqrt{2} i$

Remember to add both the real parts and the imaginary parts in this next example.

Example $\PageIndex{3}$

Simplify:

1. $(4-3 i)+(5+6 i)$
2. $(2-5 i)-(5-2 i)$

Solution:

a.

$(4-3 i)+(5+6 i)$

Use the Associative Property to put the real parts and the imaginary parts together.

$(4+5)+(-3 i+6 i)$

Simplify.

$9+3i$

b.

$(2-5 i)-(5-2 i)$

Distribute.

$2-5 i-5+2 i$

Use the Associative Property to put the real parts and the imaginary parts together.

$2-5-5 i+2 i$

Simplify.

$-3-3 i$

You Try $\PageIndex{3}$

Simplify:

1. $(2+7 i)+(4-2 i)$
2. $(8-4 i)-(2-i)$

Answer

1. $6+5i$
2. $6-3i$

Multiplying Complex Numbers

Multiplying complex numbers is also much like multiplying expressions with coefficients and variables. There is only one special case we need to consider. We will look at that after we practice in the next two examples.

Example $\PageIndex{4}$

Multiply: $2 i(7-5 i)$

Solution:

$2 i(7-5 i)$

Distribute.

$14 i-10 i^{2}$

Simplify $i^{2}$.

$14 i-10(-1)$

Multiply.

$14 i+10$

Write in standard form.

$10+14i$

You Try $\PageIndex{4}$

Multiply: $-3 i(2+4 i)$.

Answer

$12+6i$

In the next example, we multiply the binomials using the Distributive Property or FOIL.

Example $\PageIndex{5}$

Multiply: $(3+2 i)(4-3 i)$

Solution:

$(3+2 i)(4-3 i)$

Use FOIL.

$12-9 i+8 i-6 i^{2}$

Simplify $i^{2}$ and combine like terms.

$12-i-6(-1)$

Multiply.

$12-i+6$

Combine the real parts.

$18-i$

You Try $\PageIndex{5}$

Multiple: $(5-3 i)(-1-2 i)$

Answer

$-11-7i$

In the next example, we could use FOIL or the Product of Binomial Squares Pattern.

Example $\PageIndex{6}$

Multiply: $(3+2 i)^{2}$

Solution:

Table 8.8.2

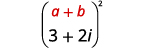Use the Product of Binomial Squares Pattern, $(a+b)^{2}=a^{2}+2 a b+b^{2}$.
Simplify.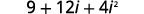
Simplify $i^{2}$.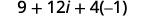
Simplify.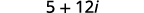

You Try $\PageIndex{6}$

Multiply: $(-2-5 i)^{2}$

Answer

$-21-20 i$

Since the square root of a negative number is not a real number, we cannot use the Product Property for Radicals. In order to multiply square roots of negative numbers we should first write them as complex numbers, using $\sqrt{-b}=\sqrt{b}i$.This is one place students tend to make errors, so be careful when you see multiplying with a negative square root.

Example $\PageIndex{7}$

Multiply: $\sqrt{-36} \cdot \sqrt{-4}$

Solution:

To multiply square roots of negative numbers, we must first write them as complex numbers.

$\sqrt{-36} \cdot \sqrt{-4}$

Write as complex numbers using $\sqrt{-b}=\sqrt{b}i$.

$\sqrt{36} i \cdot \sqrt{4} i$

Simplify.

$6 i \cdot 2 i$

Multiply.

$12i^{2}$

Simplify $i^{2}$ and multiply.

$-12$

You Try $\PageIndex{7}$

Multiply: $\sqrt{-49} \cdot \sqrt{-4}$

Answer

$-14$

In the next example, each binomial has a square root of a negative number. Before multiplying, each square root of a negative number must be written as a complex number.

Example $\PageIndex{8}$

Multiply: $(3-\sqrt{-12})(5+\sqrt{-27})$

Solution:

To multiply square roots of negative numbers, we must first write them as complex numbers.

$(3-\sqrt{-12})(5+\sqrt{-27})$

Write as complex numbers using $\sqrt{-b}=\sqrt{b}i$.

$(3-2 \sqrt{3} i)(5+3 \sqrt{3} i)$

Use FOIL.

$15+9 \sqrt{3} i-10 \sqrt{3} i-6 \cdot 3 i^{2}$

Combine like terms and simplify $i^{2}$.

$15-\sqrt{3} i-6 \cdot(-3)$

Multiply and combine like terms.

$33-\sqrt{3} i$

You Try $\PageIndex{8}$

Multiply: $(-2+\sqrt{-8})(3-\sqrt{-18})$

Answer

$6+12 \sqrt{2} i$

We first looked at conjugate pairs when we studied polynomials. We said that a pair of binomials that each have the same first term and the same last term, but one is a sum and one is a difference is called a conjugate pair and is of the form $(a−b),(a+b)$.

A complex conjugate pair is very similar. For a complex number of the form $a+bi$, its conjugate is $a−bi$. Notice they have the same first term and the same last term, but one is a sum and one is a difference.

Complex Conjugate Pairs

A complex conjugate pair is of the form $a+bi,a-bi$.

We will multiply a complex conjugate pair in the next example.

Example $\PageIndex{9}$

Multiply: $(3-2 i)(3+2 i)$

Solution:

$(3-2 i)(3+2 i)$

Use FOIL

$9+6 i-6 i-4 i^{2}$

Combine like terms and simplify $i^{2}$.

$9-4(-1)$

Multiply and combine like terms.

$13$

You Try $\PageIndex{9}$

Multiply: $(-2+5 i) \cdot(-2-5 i)$

Answer

$29$

From our study of polynomials, we know the product of conjugates is always of the form $(a-b)(a+b)=a^{2}-b^{2}$.The result is called a difference of squares. We can multiply a complex conjugate pair using this pattern.

The last example we used FOIL. Now we will use the Product of Conjugates Pattern.

Figure $\PageIndex{3}$

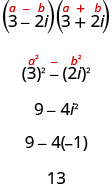
Notice this is the same result we found in Example 8.8.9.

When we multiply complex conjugates, the product of the last terms will always have an $i^{2}$ which simplifies to $−1$.

$\begin{array}{c}{(a-b i)(a+b i)} \\ {a^{2}-(b i)^{2}} \\ {a^{2}-b^{2} i^{2}} \\ {a^{2}-b^{2}(-1)} \\ {a^{2}+b^{2}}\end{array}$

This leads us to the Product of Complex Conjugates Pattern: $(a-b i)(a+b i)=a^{2}+b^{2}$

Product of Complex Conjugates

If $a$ and $b$ are real numbers, then

$(a-b i)(a+b i)=a^{2}+b^{2}$

Example $\PageIndex{10}$

Multiply: $(8-2 i)(8+2 i)$

Solution:

Table 8.8.3

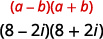Use the Product of Complex Conjugates Pattern, $(a-b i)(a+b i)=a^{2}+b^{2}$.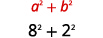
Simplify the squares.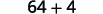
Add.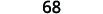

You Try $\PageIndex{10}$

Multiply: $(-5+4 i)(-5-4 i)$

Answer

$41$

Dividing Complex Numbers

Dividing complex numbers is much like rationalizing a denominator. We want our result to be in standard form with no imaginary numbers in the denominator.

Example $\PageIndex{11}$

Divide: $\frac{4+3 i}{3-4 i}$

Solution:

Table 8.8.4

Step 1: Write both the numerator and denominator in standard form.	They are both in standard form.	$\frac{4+3 i}{3-4 i}$
Step 2: Multiply the numerator and denominator by the complex conjugate of the denominator.	The complex conjugate of $3-4i$ is $3+4i$.	$\frac{(4+3 i)\color{red}{(3+4 i)}}{(3-4 i)\color{red}{(3+4 i)}}$
Step 3: Simplify and write the result in standard form.	Use the pattern $(a-b i)(a+b i)=a^{2}+b^{2}$ in the denominator. Combine like terms. Simplify. Write the result in standard form.	$\begin{array}{c}{\frac{12+16 i+9 i+12 i^{2}}{9+16}} \\ {\frac{12+25 i-12}{25}} \\ {\frac{25 i}{25}} \\ {i}\end{array}$

You Try $\PageIndex{11}$

Divide: $\frac{2+5 i}{5-2 i}$

Answer

$i$

We summarize the steps here.

How to Divide Complex Numbers

1. Write both the numerator and denominator in standard form.
2. Multiply both the numerator and denominator by the complex conjugate of the denominator.
3. Simplify and write the result in standard form.

Example $\PageIndex{12}$

Divide, writing the answers in standard form: $\frac{-3}{5+2 i}$

Solution:

$\frac{-3}{5+2 i}$

Multiply the numerator and denominator by the complex conjugate of the denominator.

$\frac{-3(5-2 i)}{(5+2 i)(5-2 i)}$

Multiply in the numerator and use the Product of Complex Conjugates Pattern in the denominator.

$\frac{-15+6 i}{5^{2}+2^{2}}$

Simplify.

$\frac{-15+6 i}{29}$

Write in standard form.

$-\frac{15}{29}+\frac{6}{29} i$

You Try $\PageIndex{12}$

Divide, writing the answer in standard form: $\frac{4}{1-4 i}$

Answer

$\frac{4}{17}+\frac{16}{17} i$

Be careful as you find the conjugate of the denominator.

Example $\PageIndex{13}$

Divide: $\frac{5+3 i}{4 i}$

Solution:

$\frac{5+3 i}{4 i}$

Write the denominator in standard form.

$\frac{5+3 i}{0+4 i}$

Multiply the numerator and denominator by the complex conjugate of the denominator.

$\frac{(5+3 i)(0-4 i)}{(0+4 i)(0-4 i)}$

Simplify.

$\frac{(5+3 i)(-4 i)}{(4 i)(-4 i)}$

Multiply.

$\frac{-20 i-12 i^{2}}{-16 i^{2}}$.

Simplify the $i^{2}$.

$\frac{-20 i+12}{16}$

Rewrite in standard form.

$\frac{12}{16}-\frac{20}{16} i$

Simplify the fractions.

$\frac{3}{4}-\frac{5}{4} i$

You Try $\PageIndex{13}$

Divide: $\frac{3+3 i}{2 i}$

Answer

$\frac{3}{2}-\frac{3}{2} i$

Simplifying Powers of $i$

The powers of $i$ make an interesting pattern that will help us simplify higher powers of $i$. Let’s evaluate the powers of $i$ to see the pattern.

$\begin{array}{ccc}{i^{1}} \qquad& {i^{2}} & {i^{3}} \qquad& {i^{4}} \\ {i} \qquad& {-1} \qquad& {i^{2}\cdot i} \qquad& {i^{2}\cdot i^{2}}\\ {}\qquad& {}\qquad& {-1\cdot i}\qquad& {(-1)(-1)}\\ {}\qquad&{}\qquad&{-i}&{1}\end{array}$

$\begin{array}{cccc}{i^{5}} \qquad& {i^{6}} \qquad& {i^{7}} \qquad& {i^{8}} \\ {i^{4} \cdot i} \qquad& {i^{4} \cdot i^{2}} \qquad& {i^{4} \cdot i^{3}} \qquad& {i^{4} \cdot i^{4}} \\ {1 \cdot i} \qquad& {1 \cdot i^{2}} \qquad& {1 \cdot i^{3}} \qquad& {1 \cdot 1} \\ {i} \qquad& {i^{2}} & {i^{3}} \qquad& {1} \\ {}&\qquad&{-1} & {-i}\end{array}$

We summarize this now.

$\begin{array}{ll}{i^{1}=i} \qquad& {i^{5}=i} \\ {i^{2}=-1} \qquad& {i^{6}=-1} \\ {i^{3}=-i} \qquad& {i^{7}=-i} \\ {i^{4}=1} \qquad& {i^{8}=1}\end{array}$

If we continued, the pattern would keep repeating in blocks of four. We can use this pattern to help us simplify powers of $i$. Since $i^{4}=1$, we rewrite each power, $i^{n}$, as a product using $i^{4}$ to a power and another power of $i$.

We rewrite it in the form $i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}$, where the exponent, $q$, is the quotient of $n$ divided by $4$ and the exponent, $r$, is the remainder from this division. For example, to simplify $i^{57}$, we divide $57$ by $4$ and we get $14$ with a remainder of $1$. In other words, $57=4⋅14+1$. So we write $i^{57}=\left(1^{4}\right)^{14} \cdot i^{1}$ and then simplify from there.

Figure $\PageIndex{4}$

Example $\PageIndex{14}$

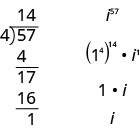
Simplify: $i^{86}$

Solution:

$i^{86}$

Divide $86$ by $4$ and rewrite $i^{86}$ in the $i^{n}=\left(i^{4}\right)^{q} \cdot i^{r}$ form.

$\left(1^{4}\right)^{21} \cdot i^{2}$

Figure $\PageIndex{5}$

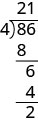
Simplify.

$(1)^{21} \cdot(-1)$

Simplify.

$-1$

You Try $\PageIndex{14}$

Simplify: $i^{75}$

Answer

$-1$