4.R: Polynomial and Rational Functions(Review)

Last updated
Save as PDF

Page ID: 87101

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Complex Numbers

Perform the indicated operation with complex numbers.

1) $(4+3 i)+(-2-5 i)$

Answer: $2-2 i$

2) $(6-5 i)-(10+3 i)$

3) $(2-3 i)(3+6 i)$

Answer: $24+3 i$

4) $\dfrac{2-i}{2+i}$

Solve the following equations over the complex number system.

5) $x^{2}-4 x+5=0$

Answer: $\{2+i, 2-i\}$

6) $x^{2}+2 x+10=0$

Quadratic Functions

For the exercises 1-2, write the quadratic function in standard form. Then, give the vertex and axes intercepts. Finally, graph the function.

1) $f(x)=x^{2}-4 x-5$

Answer

$f(x)=(x-2)^{2}-9$ vertex $(2,-9)$, intercepts $(5,0); (-1,0); (0,-5)$

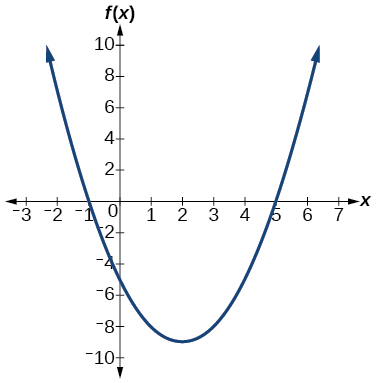
$CNX_Precalc_Figure_03_09_206.jpg$

2) $f(x)=-2 x^{2}-4 x$

For the problems 3-4, find the equation of the quadratic function using the given information.

3) The vertex is $(-2,3)$ and a point on the graph is $(3,6)$.

Answer: $f(x)=\dfrac{3}{25}(x+2)^{2}+3$

4) The vertex is $(-3,6.5)$ and a point on the graph is $(2,6)$.

Answer the following questions.

5) A rectangular plot of land is to be enclosed by fencing. One side is along a river and so needs no fence. If the total fencing available is $600$ meters, find the dimensions of the plot to have maximum area.

Answer: $300$ meters by $150$ meters, the longer side parallel to river.

6) An object projected from the ground at a $45$ degree angle with initial velocity of $120$ feet per second has height, $h$, in terms of horizontal distance traveled, $x$, given by $h(x)=\dfrac{-32}{(120)^{2}} x^{2}+x$. Find the maximum height the object attains.

Power Functions and Polynomial Functions

For the exercises 1-3, determine if the function is a polynomial function and, if so, give the degree and leading coefficient.

1) $f(x)=4 x^{5}-3 x^{3}+2 x-1$

Answer: Yes, $\text{degree} = 5$, $\text{leading coefficient} = 4$

2) $f(x)=5^{x+1}-x^{2}$

3) $f(x)=x^{2}\left(3-6 x+x^{2}\right)$

Answer: Yes, $\text{degree} = 4$, $\text{leading coefficient} = 1$

For the exercises 4-6, determine end behavior of the polynomial function.

4) $f(x)=2 x^{4}+3 x^{3}-5 x^{2}+7$

5) $f(x)=4 x^{3}-6 x^{2}+2$

Answer: As $x \rightarrow-\infty, f(x) \rightarrow-\infty $, as $x \rightarrow \infty, f(x) \rightarrow \infty$

6) $f(x)=2 x^{2}\left(1+3 x-x^{2}\right)$

Graphs of Polynomial Functions

For the exercises 1-3, find all zeros of the polynomial function, noting multiplicities.

1) $f(x)=(x+3)^{2}(2 x-1)(x+1)^{3}$

Answer: $-3$ with multiplicity $2$, $-\dfrac{1}{2}$ with multiplicity $1$, $-1$ with multiplicity $3$

2) $f(x)=x^{5}+4 x^{4}+4 x^{3}$

3) $f(x)=x^{3}-4 x^{2}+x-4$

Answer: $4$ with multiplicity $1$

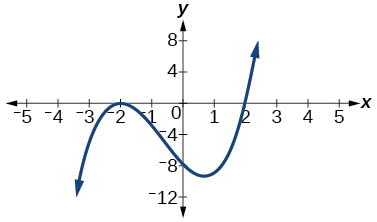
For the exercises 4-5, based on the given graph, determine the zeros of the function and note multiplicity.

$CNX_Precalc_Figure_03_09_208.jpg$

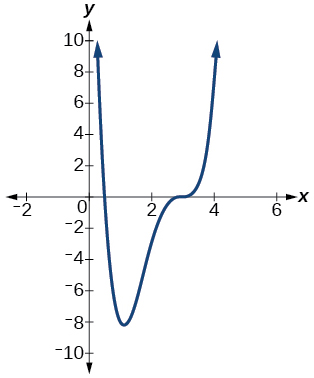
$CNX_Precalc_Figure_03_09_209.jpg$

Answer: $\dfrac{1}{2}$ with multiplicity $1$, $3$ with multiplicity $3$

6) Use the Intermediate Value Theorem to show that at least one zero lies between $2$ and $3$ for the function $f(x)=x^{3}-5 x+1$

Dividing Polynomials

For the exercises 1-2, use long division to find the quotient and remainder.

1) $\dfrac{x^{3}-2 x^{2}+4 x+4}{x-2}$

Answer: $x^{2}+4$ with remainder $12$

2) $\dfrac{3 x^{4}-4 x^{2}+4 x+8}{x+1}$

For the exercises 3-6, use synthetic division to find the quotient. If the divisor is a factor, then write the factored form.

3) $\dfrac{x^{2}-2 x^{2}+5 x-1}{x+3}$

Answer: $x^{2}-5 x+20-\dfrac{61}{x+3}$

4) $\dfrac{x^{2}+4 x+10}{x-3}$

5) $\dfrac{2 x^{3}+6 x^{2}-11 x-12}{x+4}$

Answer: $2 x^{2}-2x-3$, so factored form is $(x+4)\left(2 x^{2}-2x-3\right)$

6) $\dfrac{3 x^{4}+3 x^{3}+2 x+2}{x+1}$

Zeros of Polynomial Functions

For the exercises 1-4, use the Rational Zero Theorem to help you solve the polynomial equation.

1) $2 x^{3}-3 x^{2}-18 x-8=0$

Answer: $\left\{-2,4,-\dfrac{1}{2}\right\}$

2) $3x^{3}+11 x^{2}+8 x-4=0$

3) $2 x^{4}-17 x^{3}+46 x^{2}-43 x+12=0$

Answer: $\left\{1,3,4, \dfrac{1}{2}\right\}$

style="display:inline !important;float:none;background-color:transparent;font-family:lato,arial,helvetica,sans-serif,arial unicode ms;font-style:normal;font-variant:normal;font-weight:400;letter-spacing:normal;line-height:22.4px;orphans:2;text-align:justify;text-decoration:none;text-indent:0px;text-transform:none;-webkit-text-stroke-width:0px;white-space:normal;word-spacing:0px;">4) $4 x^{4}+8 x^{3}+19 x^{2}+32 x+12=0$

For the exercises 5-6, use Descartes’ Rule of Signs to find the possible number of positive and negative solutions.

5) $x^{3}-3 x^{2}-2 x+4=0$

Answer: $0$ or $2$ positive, $1$ negative

6) $2 x^{4}-x^{3}+4 x^{2}-5 x+1=0$

Rational Functions

For the following rational functions 1-4, find the intercepts and the vertical and horizontal asymptotes, and then use them to sketch a graph.

1) $f(x)=\dfrac{x+2}{x-5}$

Answer

Intercepts $(-2,0)$ and $\left(0,-\dfrac{2}{5}\right)$, Asymptotes $x=5$ and $y=1$

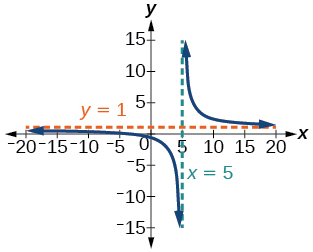
$CNX_Precalc_Figure_03_09_210.jpg$

2) $f(x)=\dfrac{x^{2}+1}{x^{2}-4}$

3) $f(x)=\dfrac{3 x^{2}-27}{x^{2}-9}$

Answer

Intercepts $(3,0),(-3,0)$, and $\left(0, \dfrac{27}{2}\right)$, Asymptotes $x=1, x=-2, y=3$

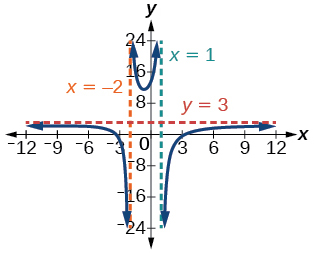
$CNX_Precalc_Figure_03_09_212.jpg$

4) $f(x)=\dfrac{x+2}{x^{2}-9}$

For the exercises 5-6, find the slant asymptote.

5) $f(x)=\dfrac{x^{2}-1}{x+2}$

Answer: $y=x-2$

6) $f(x)=\dfrac{2 x^{3}-x^{2}+4}{x^{2}+1}$

Inverses and Radical Functions

For the exercises 1-6, find the inverse of the function with the domain given.

1) $f(x)=(x-2)^{2}, x \geq 2$

Answer: $f^{-1}(x)=\sqrt{x}+2$

2) $f(x)=(x+4)^{2}-3, x \geq-4$

3) $f(x)=x^{2}+6 x-2, x \geq-3$

Answer: $f^{-1}(x)=\sqrt{x+11}-3$

4) $f(x)=2 x^{3}-3$

5) $f(x)=\sqrt{4 x+5}-3$

Answer: $f^{-1}(x)=\dfrac{(x+3)^{2}-5}{4}, x \geq-3$

6) $f(x)=\dfrac{x-3}{2 x+1}$

Modeling Using Variation

For the exercises 1-4, find the unknown value.

1) $y$ varies directly as the square of $x$. If when $x=3, y=36$, find $y$ if $x=4$.

Answer: $y=64$

2) $y$ varies inversely as the square root of $x$. If when $x=25, y=2$, find $y$ if $x=4$.

3) $y$ varies jointly as the cube of $x$ and as $z$. If when $x=1$ and $z=2, y=6$, find $y$ if $x=2$ and $z=3$.

Answer: $y=72$

4) $y$ varies jointly as $x$ and the square of $z$ and inversely as the cube of $w$. If when $x=3, z=4$, and $w=2, y=48$, ind $y$ if $x=4, z=5$, and $w=3$.

For the exercises 5-6, solve the application problem.

5) The weight of an object above the surface of the earth varies inversely with the distance from the center of the earth. If a person weighs $150$ pounds when he is on the surface of the earth ($3,960$ miles from center), find the weight of the person if he is $20$ miles above the surface.

Answer: $148.5$ pounds

6) The volume $V$ of an ideal gas varies directly with the temperature $T$ and inversely with the pressure$P$. A cylinder contains oxygen at a temperature of $310$ degrees K and a pressure of $18$ atmospheres in a volume of $120$ liters. Find the pressure if the volume is decreased to $100$ liters and the temperature is increased to $320$ degrees K.

Practice Test

Perform the indicated operation or solve the equation.

1) $(3-4 i)(4+2 i)$

Answer: $20-10 i$

2) $\dfrac{1-4 i}{3+4 i}$

3) $x^{2}-4 x+13=0$

Answer: $\{2+3 i, 2-3 i\}$

4) Give the degree and leading coefficient of the following polynomial function. \[f(x)=x^{3}\left(3-6 x^{2}-2 x^{2}\right) \nonumber \]

Determine the end behavior of the polynomial function.

5) $f(x)=8 x^{3}-3 x^{2}+2 x-4$

Answer: As $x \rightarrow-\infty, f(x) \rightarrow-\infty$, as $x \rightarrow \infty, f(x) \rightarrow \infty$

6) $f(x)=-2 x^{2}\left(4-3 x-5 x^{2}\right)$

7) Write the quadratic function in standard form. Determine the vertex and axes intercepts and graph the function. \[f(x)=x^{2}+2 x-8 \nonumber \]

Answer

$f(x)=(x+1)^{2}-9,$ vertex $(-1,-9),$ intercepts $(2,0); (-4,0); (0,-8)$

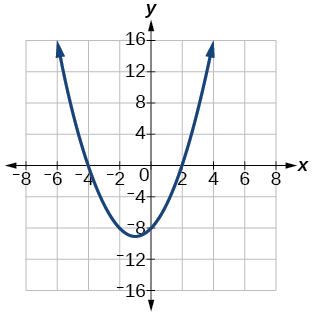
$CNX_Precalc_Figure_03_09_214.jpg$

8) Given information about the graph of a quadratic function, find its equation: Vertex $(2,0)$ and point on graph $(4,12)$

Solve the following application problem.

9) A rectangular field is to be enclosed by fencing. In addition to the enclosing fence, another fence is to divide the field into two parts, running parallel to two sides. If $1,200$ feet of fencing is available, find the maximum area that can be enclosed.

Answer: $60,000$ square feet

Find all zeros of the following polynomial functions, noting multiplicities.

10) $f(x)=(x-3)^{3}(3 x-1)(x-1)^{2}$

11) $f(x)=2 x^{6}-12 x^{5}+18 x^{4}$

Answer: $0$ with multiplicity $4$, $3$ with multiplicity $2$

12) Based on the graph, determine the zeros of the function and multiplicities.

$CNX_Precalc_Figure_03_09_215.jpg$

13) Use long division to find the quotient: \[\dfrac{2 x^{2}+3 x-4}{x+2} \nonumber \]

Answer: $2 x^{2}-4 x+11-\dfrac{26}{x+2}$

Use synthetic division to find the quotient. If the divisor is a factor, write the factored form.

14) $\dfrac{x^{4}+3 x^{2}-4}{x-2}$

15) $\dfrac{2 x^{3}+5 x^{2}-7 x-12}{x+3}$

Answer: $2 x^{2}-x-4$. So factored form is $(x+3)\left(2 x^{2}-x-4\right)$

Use the Rational Zero Theorem to help you find the zeros of the polynomial functions.

16) $f(x)=2 x^{3}+5 x^{2}-6 x-9$

17) $f(x)=4 x^{4}+8 x^{3}+21 x^{2}+17 x+4$

Answer: $-\dfrac{1}{2}$ (has multiplicity $2$), $\dfrac{-1+i \sqrt{15}}{2}$

18) $f(x)=4 x^{4}+16 x^{3}+13 x^{2}-15 x-18$

19) $f(x)=x^{5}+6 x^{4}+13 x^{3}+14 x^{2}+12 x+8$

Answer: $-2$ (has multiplicity $3$), $\pm i$

Given the following information about a polynomial function, find the function.

20) It has a double zero at $x=3$ and zeroes at $x=1$ and $x=-2$. Its $y$ -intercept is $(0,12)$.

21) It has a zero of multiplicity $3$ at $x=\dfrac{1}{2}$ and another zero at $x=-3$. It contains the point $(1,8)$.

Answer: $f(x)=2(2 x-1)^{3}(x+3)$

22) Use Descartes’ Rule of Signs to determine the possible number of positive and negative solutions. \[8 x^{3}-21 x^{2}+6=0 \nonumber \]

For the following rational functions, find the intercepts and horizontal and vertical asymptotes, and sketch a graph.

23) $f(x)=\dfrac{x+4}{x^{2}-2 x-3}$

Answer

Intercepts $(-4,0)$, $\left(0,-\dfrac{4}{3}\right)$, Asymptotes $x=3, x=-1, y=0$

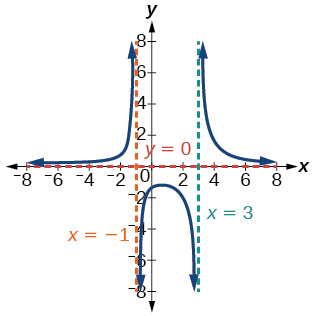
$CNX_Precalc_Figure_03_09_216.jpg$

24) $f(x)=\dfrac{x^{2}+2 x-3}{x^{2}-4}$

25) Find the slant asymptote of the rational function. \[f(x)=\dfrac{x^{2}+3 x-3}{x-1} \nonumber \]

Answer: $y=x+4$

Find the inverse of the function.

26) $f(x)=\sqrt{x-2}+4$

27) $f(x)=3 x^{3}-4$

Answer: $f^{-1}(x)=\sqrt[3]{\dfrac{x+4}{3}}$

28) $f(x)=\dfrac{2 x+3}{3 x-1}$

Find the unknown value.

29) $y$ varies inversely as the square of $x$ and when $x=3, y=2$. Find $y$ if $x=1$.

Answer: $y=18$

30) $y$ varies jointly with $x$ and the cube root of $z$. If when $x=27, y=12$, find $y$ if $x=5$ and $z=8$.

Solve the following application problem.

31) The distance a body falls varies directly as the square of the time it falls. If an object falls $64$ feet in $2$ seconds, how long will it take to fall $256$ feet?

Answer: $4$ seconds

Search

Text Color

Text Size

Margin Size

Font Type