5.4: Logarithmic Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Convert from logarithmic to exponential form.
- Convert from exponential to logarithmic form.
- Evaluate logarithms.
- Use common logarithms.
- Use natural logarithms.
- Finding inverses of exponential and logarithmic functions.
In 2010, a major earthquake struck Haiti, destroying or damaging over 285,000 homes. One year later, another, stronger earthquake devastated Honshu, Japan, destroying or damaging over 332,000 buildings, like those shown in Figure 5.4.1. Even though both caused substantial damage, the earthquake in 2011 was 100 times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a 7.0 on the Richter Scale whereas the Japanese earthquake registered a 9.0.

Figure 5.4.1: Devastation of March 11, 2011 earthquake in Honshu, Japan. (credit: Daniel Pierce).
The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude 8 is not twice as great as an earthquake of magnitude 4. It is
108−4=104=10,000
times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
Converting from Logarithmic to Exponential Form
In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake were 500 times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is 10x=500, where x represents the difference in magnitudes on the Richter Scale. How would we solve for x?
We have not yet learned a method for solving exponential equations. None of the algebraic tools discussed so far is sufficient to solve 10x=500. We know that 102=100 and 103=1000, so it is clear that x must be some value between 2 and 3, since y=10x is increasing. We can examine a graph, as in Figure 5.4.2, to better estimate the solution.
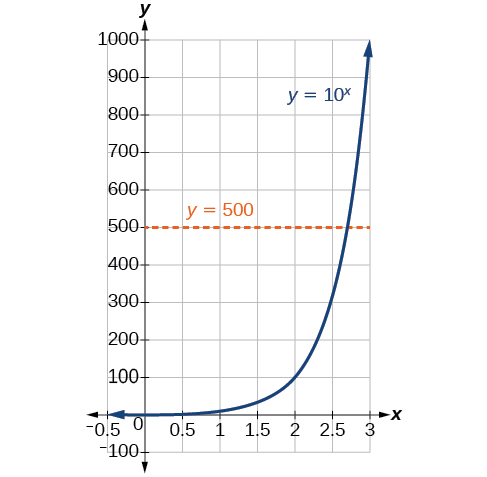
Figure 5.4.2
Estimating from a graph, however, is imprecise. To find an algebraic solution, we must introduce a new function. Observe that the graph in Figure 5.4.2 passes the horizontal line test. The exponential function y=bx is one-to-one, so its inverse, x=by is also a function. As is the case with all inverse functions, we simply interchange x and y and solve for y to find the inverse function. To represent y as a function of x, we use a logarithmic function of the form y=logb(x). The base b logarithm of a number is the exponent by which we must raise b to get that number.
We read a logarithmic expression as, “The logarithm with base b of x is equal to y,” or, simplified, “log base b of x is y.” We can also say, “b raised to the power of y is x,” because logs are exponents. For example, the base 2 logarithm of 32 is 5, because 5 is the exponent we must apply to 2 to get 32. Since 25=32, we can write log232=5. We read this as “log base 2 of 32 is 5.”
We can express the relationship between logarithmic form and its corresponding exponential form as follows:
logb(x)=y⇔by=x,b>0,b≠1
Note that the base b is always positive.
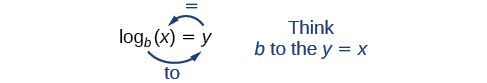
Because logarithm is a function, it is most correctly written as logb(x), using parentheses to denote function evaluation, just as we would with f(x). However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as logbx. Note that many calculators require parentheses around the x.
We can illustrate the notation of logarithms as follows:

Notice that, comparing the logarithm function and the exponential function, the input and the output are switched. This means y=logb(x) and y=bx are inverse functions.
A logarithm base b of a positive number x satisfies the following definition.
For x>0, b>0, b≠1,
y=logb(x) is equivalent to by=x
where,
- we read logb(x) as, “the logarithm with base b of x” or the “log base b of x."
- the logarithm y is the exponent to which b must be raised to get x.
Also, since the logarithmic and exponential functions switch the x and y values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,
- the domain of the logarithm function with base b is (0,∞).
- the range of the logarithm function with base b is (−∞,∞).
We call the input, x, the argument of the function.
Write the following logarithmic equations in exponential form.
- log3(9)=2
- log6(√6)=12
- log5(1)=0
- log10(1,000,000)=6
Solution
First, identify the values of b, y,and x. Then, write the equation in the form by=x.
- log3(9)=2
Here, b=3, y=2,and x=9. Therefore, the equation log3(9)=2 is equivalent to 32=9
- log6(√6)=12
Here, b=6, y=12,and x=√6. Therefore, the equation log6(√6)=12 is equivalent to 612=√6
- log5(1)=0
Here, b=5, y=0,and x=1. Therefore, the equation log5(1)=0 is equivalent to
50=1
Write the following logarithmic equations in exponential form.
- log10(1,000,000)=6
- log5(25)=2
- Answer a
-
log10(1,000,000)=6 is equivalent to 106=1,000,000
- Answer b
-
log5(25)=2 is equivalent to 52=25
By establishing the relationship between exponential and logarithmic functions, we can now solve basic logarithmic equations by rewriting them in exponential form.
Solve log4(x)=2 for x.
Solution
By rewriting this expression as an exponential, 42=x, so x=16.
Solve log2(t)=5 for t.
- Answer
-
t=32
Converting from Exponential to Logarithmic Form
To convert from exponents to logarithms, we follow the same steps in reverse. We identify the base b,exponent x,and output y. Then we write x=logb(y).
Write the following exponential equations in logarithmic form.
- 23=8
- 42=16
- 10−4=110,000
Solution
First, identify the values of b, y,and x. Then, write the equation in the form x=logb(y).
- 23=8
Here, b=2, x=3,and y=8. Therefore, the equation 23=8 is equivalent to log2(8)=3.
- 42=16
Here, b=4, x=2,and y=16. Therefore, the equation 42=16 is equivalent to log4(16)=2.
- 10−4=110,000
Here, b=10, x=−4,and y=110,000. Therefore, the equation 10−4=110,000 is equivalent to log10(110,000)=−4.
Write the following exponential equations in logarithmic form.
- 32=9
- 53=125
- 2−1=12
- Answer a
-
32=9 is equivalent to log3(9)=2
- Answer b
-
53=125 is equivalent to log5(125)=3
- Answer c
-
2−1=12 is equivalent to log2(12)=−1
By establishing the relationship between exponential and logarithmic functions, we can now solve basic exponential equations also.
Solve 2x=10 for x.
Solution
By rewriting this expression as a logarithm, we get x=log2(10).
Solve 3m=11 for m.
- Answer
-
m=log3(11)
Evaluating Logarithms
Knowing the squares, cubes, and roots of numbers allows us to evaluate many logarithms mentally. For example, consider log28. We ask, “To what exponent must 2 be raised in order to get 8?” Because we already know 23=8, it follows that log28=3.
Now consider solving log749 and log327 mentally.
- We ask, “To what exponent must 7 be raised in order to get 49?” We know 72=49. Therefore, log749=2
- We ask, “To what exponent must 3 be raised in order to get 27?” We know 33=27. Therefore, log327=3
Even some seemingly more complicated logarithms can be evaluated without a calculator. For example, let’s evaluate log2349 mentally.
- We ask, “To what exponent must 23 be raised in order to get 49? ” We know 22=4 and 32=9, so (23)2=49. Therefore, log23(49)=2.
Evaluate the following without using a calculator:
- log4(64)
- log3(127)
- log5(−3)
Solution
- First let's set the expression equal to y, y=log4(64), then we can rewrite the logarithm in exponential form: 4y=64. Next, we ask, “To what exponent must 4 be raised in order to get 64?”
We know
43=64
So
4y=43
Therefore,
log4(64)=3
- First, set the expression equal to a variable, y=log3(127), Then rewrite the logarithm in exponential form: 3y=127. Next, we ask, “To what exponent must 3 be raised in order to get 127?”
We know 33=27,but what must we do to get the reciprocal, 127? Recall from working with exponents that b−a=1ba. We use this information to write
3−3=133=127
Therefore, log3(127)=−3.
- Logarithms are only defined for positive values so y=log5(−3) is undefined.
Evaluate the following without using a calculator:
- log121(11)
- log2(132)
- Answer
-
- log121(11)=12
- log2(132)=−5
Properties of Logarithms
We saw above that it was convenient to convert to exponential form to evaluate logarithms. Recall that log4(64)=3. We know that 43=64, so we substitute this in, we get log4(64)=log4(43)=3
This gives us our first property for logarithms:
logb(bx)=x
Next, consider x=log31. Converting to exponential form, 3x=1. From properties of exponents we know x=0. We can conclude that \({\log}_31\=0). This bring sus to our second property for logarithms:
logb1=0
Similarly, if we convert x=logbb to exponetial form we will find that x=logbb=1. This is our third property for logarithms:
logbb=1
To evaluate x=4log4(9), we can rewrite in logarithmic form as log49=log4x. This means x=9. This give us the following property:
blogbx=x where x>0
- logb(bx)=x
- logb1=0
- logbb=1
- blogbx=x where x>0
Common Logarithms
Sometimes we may see a logarithm written without a base. In this case, we assume that the base is 10. In other words, the expression log(x) means log10(x). We call a base 10 logarithm a common logarithm. Common logarithms are used to measure the Richter Scale mentioned at the beginning of the section. Scales for measuring the brightness of stars and the pH of acids and bases also use common logarithms.
A common logarithm is a logarithm with base 10. We write log10(x) simply as log(x). The common logarithm of a positive number x satisfies the following definition.
For x>0,
y=log(x) is equivalent to 10y=x
We read log(x) as, “the logarithm with base 10 of x ” or “log base 10 of x.”
The logarithm y is the exponent to which 10 must be raised to get x.
Evaluate y=log(1000) without using a calculator.
Solution
First we rewrite the logarithm in exponential form: 10y=1000. Next, we ask, “To what exponent must 10 be raised in order to get 1000?” We know
103=1000
Therefore, log(1000)=3.
Evaluate y=log(1,000,000) without using a calculator.
- Answer
-
log(1,000,000)=6
Evaluate y=log(321) and round to four decimal places using a calculator.
Solution
Rounding to four decimal places, log(321)≈2.5065.
Analysis
Note that 102=100 and that 103=1000. Since 321 is between 100 and 1000, we know that log(321) must be between log(100) and log(1000). This gives us the following:
100<321<1000
2<2.5065<3
When using a calculator when approximating logarithms, it is important to make sure you input everything properly including having parentheses in the corect place.
Use your calculator to approximate log3−4 to four decimal places.
Solution
Remember that sometimes parentheses are not written, log3−4 is equivalent to log(3)−4.
log3−4≈−3.5229
Evaluate y=log(123) and round to four decimal places using a calculator.
- Answer
-
log(123)≈2.0899
The amount of energy released from one earthquake was 500 times greater than the amount of energy released from another. The equation 10x=500 represents this situation, where x is the difference in magnitudes on the Richter Scale. Rounding to three decimal places, what was the difference in magnitudes?
Solution
We begin by rewriting the exponential equation in logarithmic form.
10x=500
log(500)=x Use the definition of the common log.
Next we evaluate the logarithm using a calculator:
To the nearest thousandth, log(500)≈2.699.
The difference in magnitudes was about 2.699.
The amount of energy released from one earthquake was 8,500 times greater than the amount of energy released from another. The equation 10x=8500 represents this situation, where x is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
- Answer
-
The difference in magnitudes was about 3.929.
Natural Logarithms
The most frequently used base for logarithms is e. Base e logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base e logarithm, loge(x), has its own notation,ln(x). Most values of ln(x) can be found only using a calculator. The major exception is that, because the logarithm of 1 is always 0 in any base, ln1=0. For other natural logarithms, we can use the ln key that can be found on most scientific calculators. We can also find the natural logarithm of any power of e using the inverse property of logarithms.
A natural logarithm is a logarithm with base e. We write loge(x) simply as ln(x). The natural logarithm of a positive number x satisfies the following definition.
For x>0,
y=ln(x) is equivalent to ey=x
We read ln(x) as, “the logarithm with base e of x” or “the natural logarithm of x.”
The logarithm y is the exponent to which e must be raised to get x.
Since the functions y=ex and y=ln(x) are inverse functions, ln(ex)=x for all x and eln(x)=x for x>0.
Approximate y=ln(500) to four decimal places using a calculator.
Solution
Rounding to four decimal places, ln(500)≈6.2146
Approximate ln(−500) to four decimal places using a calculator.
- Answer
-
It is not possible to take the logarithm of a negative number so ln(−500) is undefined.
Solve ln(a)=7 for a.
- Answer
-
a=e7
Note that this answer is exact as e is an irrational number. To represent as a decimal approximation when asked, use your calculator to approximate.
There a couple of things worth mentioning from what we have learned about logarithms in this section.
- Logarithms are functions, f(x)=logb(x). We call the input, x, the argument of the function.
- When evaluating, sometimes we do not write parentheses around the argument. Example: log7(4) is equivalent to log74
- Common logarithms are written as y=log(x). All other logarithms, excluding the natural logarithm must have the base written or else it is assumed to be a common logarithm
- The natural logarithm is written as y=ln(x). This is the only logarithm with a function name, ln, that is different than all other logarithms.
Let's end with some examples of using the relationship between exponential and logarithmic functions to find inverse functions.
Given J(x)=log3(x−2)+4, find J−1
Solution
J(x)=log3(x−2)+4y=log3(x−2)+4x=log3(y−2)+4x−4=log3(y−2)3x−4=y−23x−4+2=y
Hence J−1=3x−4+2
Notice that J(x) is a basic logarithm function of base 3 that has a horizontal shift to the right 2 units and a vertical shift up 4 units. J−1 has a horizontal shift to the right 4 units and a vertical shift up 2 units. When working with transformed functions, the inverse will have its transformations reversed between the horizontal and vertical directions. Remember that the domain and range of functions and their inverse are also reversed.
Find the inverse of V(x)=5−ex+3
- Answer
-
y=ln(5−x)−3


