5.5: Graphing Logarithmic Functions
- Page ID
- 90194
- Identify the domain of logarithmic functions.
- Identify transformations of logarithmic functions.
- Graph logarithmic functions.
- Find equations of logarithmic functions that model graphical information.
Earlier in this chapter, we saw how creating a graphical representation of an exponential model gives us another layer of insight for predicting future events. How do logarithmic graphs give us insight into situations? Because every logarithmic function is the inverse function of an exponential function, we can think of every output on a logarithmic graph as the input for the corresponding inverse exponential equation. In other words, logarithms give the cause for an effect.
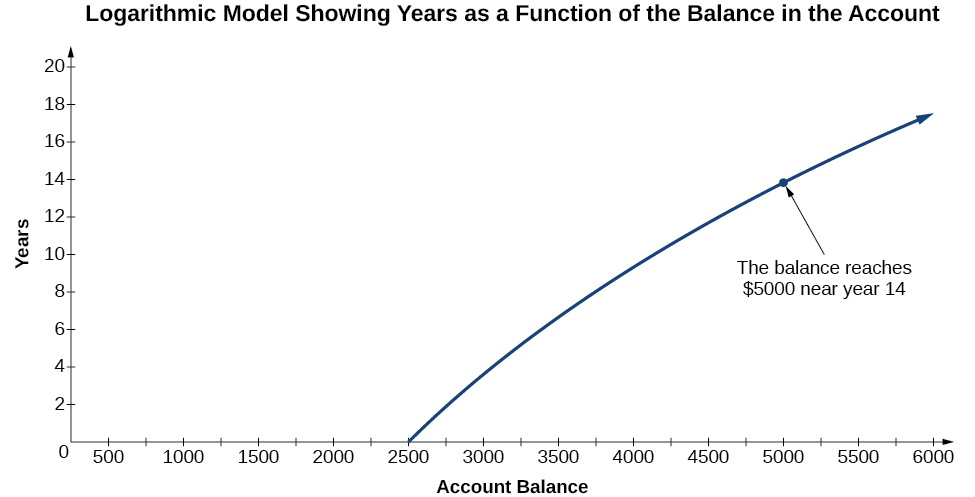
To illustrate, suppose we invest \($2500\) in an account that offers an annual interest rate of 5%, compounded continuously. We already know that the balance in our account for any year \(t\) can be found with the equation \(A=2500e^{0.05t}\).
But what if we wanted to know the year for any balance? We would need to create a corresponding new function by interchanging the input and the output; thus we would need to create a logarithmic model for this situation. By graphing the model, we can see the output (year) for any input (account balance). For instance, what if we wanted to know how many years it would take for our initial investment to double? Figure \(\PageIndex{1}\) shows this point on the logarithmic graph.
In this section we will discuss the values for which a logarithmic function is defined, and then turn our attention to graphing the family of logarithmic functions.
Finding the Domain of a Logarithmic Function
Before working with graphs, we will take a look at the domain (the set of input values) for which the logarithmic function is defined.
Recall that the exponential function is defined as \(y=b^x\) for any real number \(x\) and constant \(b>0\), \(b≠1\), where
- The domain of \(y\) is \((−\infty,\infty)\).
- The range of \(y\) is \((0,\infty)\).
In the last section, we learned that the logarithmic function \(y={\log}_b(x)\) is the inverse of the exponential function \(y=b^x\). So, as inverse functions:
- The domain of \(y={\log}_b(x)\) is the range of \(y=b^x\): \((0,\infty)\).
- The range of \(y={\log}_b(x)\) is the domain of \(y=b^x\): \((−\infty,\infty)\).
Transformations of the basic function \(y={\log}_b(x)\) behave similarly to those of other functions. Just as with other basic functions, we can apply the four types of transformations—shifts, stretches, compressions, and reflections—to the basic function without loss of shape.
We've seen that certain transformations can change the range of \(y=b^x\). Similarly, applying transformations to the basic function \(y={\log}_b(x)\) can change the domain. When finding the domain of a logarithmic function, it is important to remember that the domain consists only of positive real numbers. That is, the argument of the logarithmic function must be greater than zero.
For example, consider \(f(x)={\log}_4(2x−3)\). This function is defined for any values of \(x\) such that the argument, in this case \(2x−3\), is greater than zero. To find the domain, we set up an inequality and solve for \(x\):
\[\begin{align*} 2x-3&> 0 \qquad \text {Show the argument greater than zero}\\ 2x&> 3 \qquad \text{Add 3} \\ x&>\dfrac{3}{2} \qquad \text{Divide by 2} \\ \end{align*}\]
In interval notation, the domain of \(f(x)={\log}_4(2x−3)\) is \(\left(\dfrac{3}{2},\infty\right)\).
Find the domain of the following functions:
- \(f(x)={\log}_2(x+3)\)
- \(g(t)=4-{\log}(5−2t)\)
Solution
- The logarithmic function is defined only when the input is positive, so this function is defined when \(x+3>0\). Solving this inequality,
\[\begin{align*} x+3&> 0 \qquad \text{The input must be positive}\\ x&> -3 \qquad \text{Subtract 3} \end{align*}\]
The domain of \(f(x)={\log}_2(x+3)\) is \((−3,\infty)\).
- This function is defined when \(5–2t>0\). Solving this inequality,
\[\begin{align*} 5-2t&> 0 \qquad \text{The input must be positive}\\ -2t&> -5 \qquad \text{Subtract 5}\\ t&< \dfrac{5}{2} \qquad \text{Divide by -2 and switch the inequality} \end{align*}\]
The domain of \(g(t)=4-{\log}(5−2t)\) is \(\left(–\infty,\dfrac{5}{2}\right)\).
What is the domain of \(h(x)=\log_4(x^2-4x+3)+2\)?
Solution
This function is defined when \(x^2-4x+3>0\). Solving this inequality using a sign chart,
\[\begin{align*} x^2-4x+3&> 0 \\[16pt] (x-3)(x-1)&>0 \end{align*} \]
.png?revision=1)
The domain is \((−3,\infty)\)
What is the domain of \(f(x)=\log(3x+7)+2\)?
- Answer
-
\((-/dfrac{7}{3},\infty)\)
Graphing Logarithmic Functions
Now that we have a feel for the set of values for which a logarithmic function is defined, we move on to graphing logarithmic functions. The family of logarithmic functions includes the basic function \(y={\log}_b(x)\) along with all its transformations: shifts, stretches, compressions, and reflections.
We begin with the basic function \(y={\log}_b(x)\). Because every logarithmic function of this form is the inverse of an exponential function with the form \(y=b^x\), their graphs will be reflections of each other across the line \(y=x\). To illustrate this, we can observe the relationship between the input and output values of \(y=2^x\) and its equivalent \(x={\log}_2(y)\) in Table \(\PageIndex{1}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(2^x=y\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \({\log}_2(y)=x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
Using the inputs and outputs from Table \(\PageIndex{1}\), we can build another table to observe the relationship between points on the graphs of the inverse functions \(f(x)=2^x\) and \(g(x)={\log}_2(x)\). See Table \(\PageIndex{2}\).
| \(f(x)=2^x\) | \(\left(−3,\dfrac{1}{8}\right)\) | \(\left(−2,\dfrac{1}{4}\right)\) | \(\left(−1,\dfrac{1}{2}\right)\) | \((0,1)\) | \((1,2)\) | \((2,4)\) | \((3,8)\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\log}_2(x)\) | \(\left(\dfrac{1}{8},−3\right)\) | \(\left(\dfrac{1}{4},−2\right)\) | \(\left(\dfrac{1}{2},−1\right)\) | \((1,0)\) | \((2,1)\) | \((4,2)\) | \((8,3)\) |
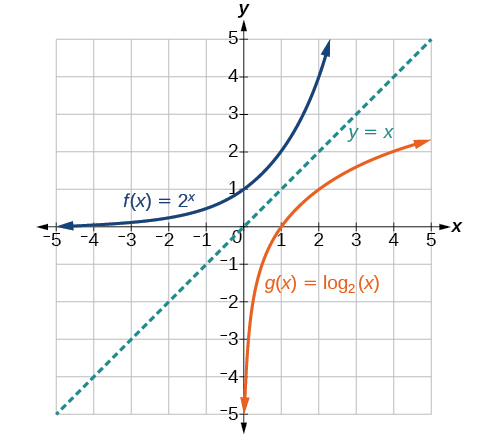
As we’d expect, the \(x\)- and \(y\)-coordinates are reversed for the inverse functions. Figure \(\PageIndex{3}\) shows the graph of \(f\) and \(g\).
Observe the following from the graph:
- \(f(x)=2^x\) has a \(y\)-intercept at \((0,1)\) and \(g(x)={\log}_2(x)\) has an \(x\)- intercept at \((1,0)\).
- The domain of \(f(x)=2^x\), \((−\infty,\infty)\), is the same as the range of \(g(x)={\log}_2(x)\).
- The range of \(f(x)=2^x\), \((0,\infty)\), is the same as the domain of \(g(x)={\log}_2(x)\).
For any real number \(x\) and constant \(b>0\), \(b≠1\), we can see the following characteristics in the graph of \(f(x)={\log}_b(x)\):
- one-to-one function
- vertical asymptote: \(x=0\)
- domain: \((0,\infty)\)
- range: \((−\infty,\infty)\)
- \(x\)-intercept: \((1,0)\)
- \(y\)-intercept: none
- point at \((b,1)\)
- increasing if \(b>1\)
- decreasing if \(0<b<1\)
Figure \(\PageIndex{4}\) compares the graphs of logarithmic functions with \(b>1\) and \(0<b<1\)
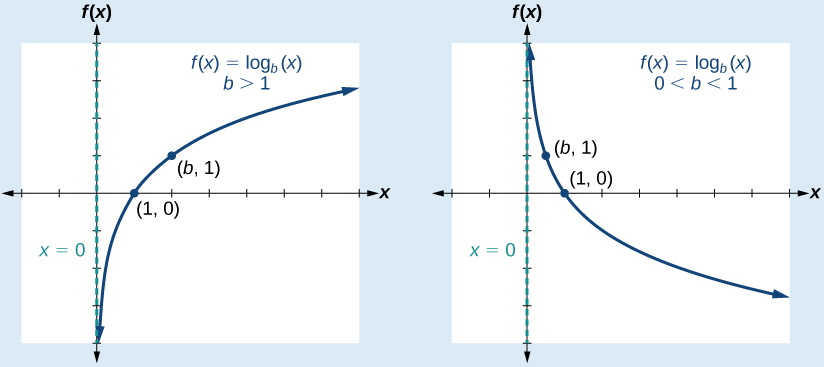
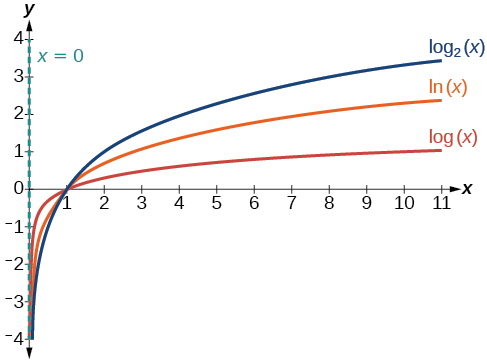
Figure \(\PageIndex{5}\) shows how changing the base \(b\) in \(f(x)={\log}_b(x)\) can affect the graphs. Observe that the graphs compress vertically as the value of the base increases. (Note: recall that the function \(\ln(x)\) has base \(e≈2.718\).)
Sketch the graph of \(f(x)={\log}_5(x)\). State the domain, range, and asymptote.
Solution
Before graphing, identify the behavior and key points for the graph.
- Since \(b=5\) is greater than one, we know the function is increasing. The left tail of the graph will approach the vertical asymptote, \(x=0\), and the right tail will increase slowly without bound.
- The \(x\)-intercept is \((1,0)\).
- The point \((5,1)\) is on the graph.
- We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points (see Figure \(\PageIndex{6}\)).
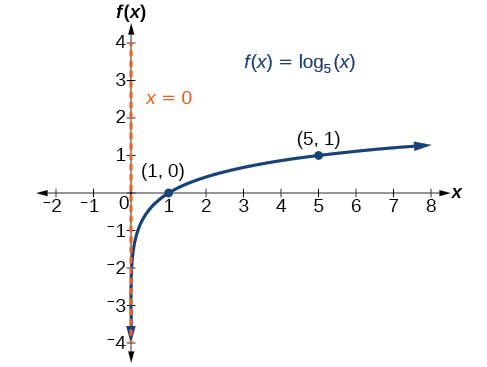
The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).
Graphing Transformations of Logarithmic Functions
As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other basic functions. We can shift, stretch, compress, and reflect the basic function \(y={\log}_b(x)\) without loss of shape.
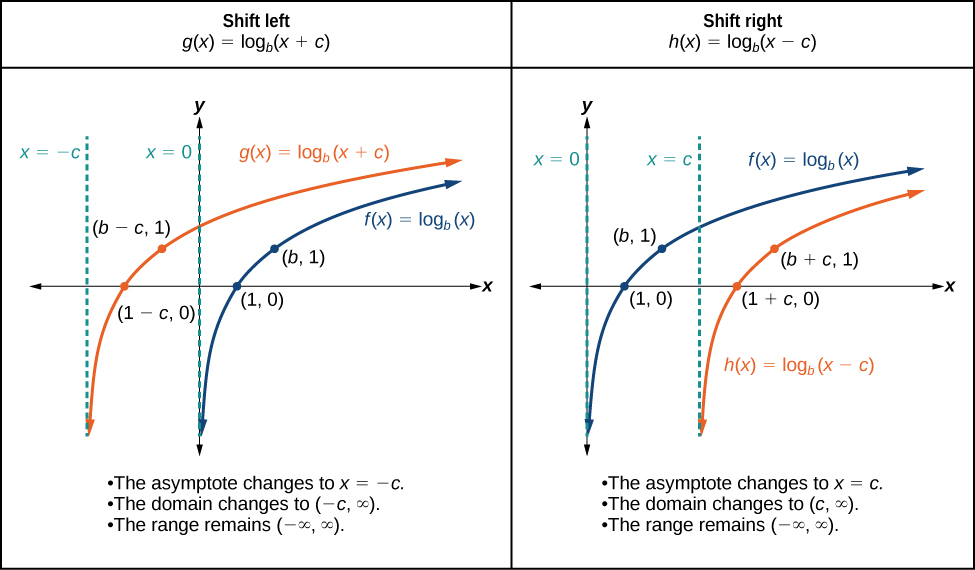
Graphing a Horizontal Shift
When a constant \(c\) is added to the input of the basic function \(f(x)={\log}_b(x)\), the result is a horizontal shift \(c\) units in the opposite direction of the sign on \(c\). To visualize horizontal shifts, we can observe the general graph of the basic function \(f(x)={\log}_b(x)\) and for \(c>0\) alongside the shift left, \(g(x)={\log}_b(x+c)\), and the shift right, \(h(x)={\log}_b(x−c)\). See Figure \(\PageIndex{7}\).
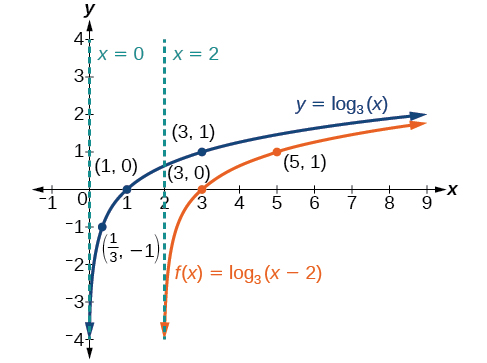
Sketch the horizontal shift \(f(x)={\log}_3(x−2)\) alongside its basic function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.
Solution
Since the function is \(f(x)={\log}_3(x−2)\), we notice \(x+(−2)=x–2\).
Thus \(c=−2\), so \(c<0\). This means we will shift the function \(f(x)={\log}_3(x)\) right 2 units.
The vertical asymptote is \(x=−(−2)\) or \(x=2\).
Consider the three key points from the basic function, \(\left(\dfrac{1}{3},−1\right)\), \((1,0)\), and \((3,1)\).
The new coordinates are found by adding \(2\) to the \(x\) coordinates.
Label the points \(\left(\dfrac{7}{3},−1\right)\), \((3,0)\),and \((5,1)\).
The domain is \((2,\infty)\),the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=2\).
Sketch a graph of \(f(x)={\log}_3(x+4)\) alongside its basic function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.
- Answer
-
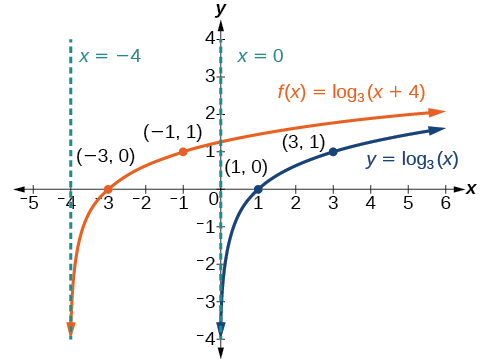
Figure \(\PageIndex{9}\) The domain is \((−4,\infty)\),the range \((−\infty,\infty)\),and the asymptote \(x=–4\).
Graphing a Vertical Shift
When a constant \(d\) is added to the basic function \(f(x)={\log}_b(x)\),the result is a vertical shift \(d\) units in the direction of the sign on \(d\). To visualize vertical shifts, we can observe the general graph of the basic function \(f(x)={\log}_b(x)\) alongside the shift up, \(g(x)={\log}_b(x)+d\) and the shift down, \(h(x)={\log}_b(x)−d\).See Figure \(\PageIndex{10}\).
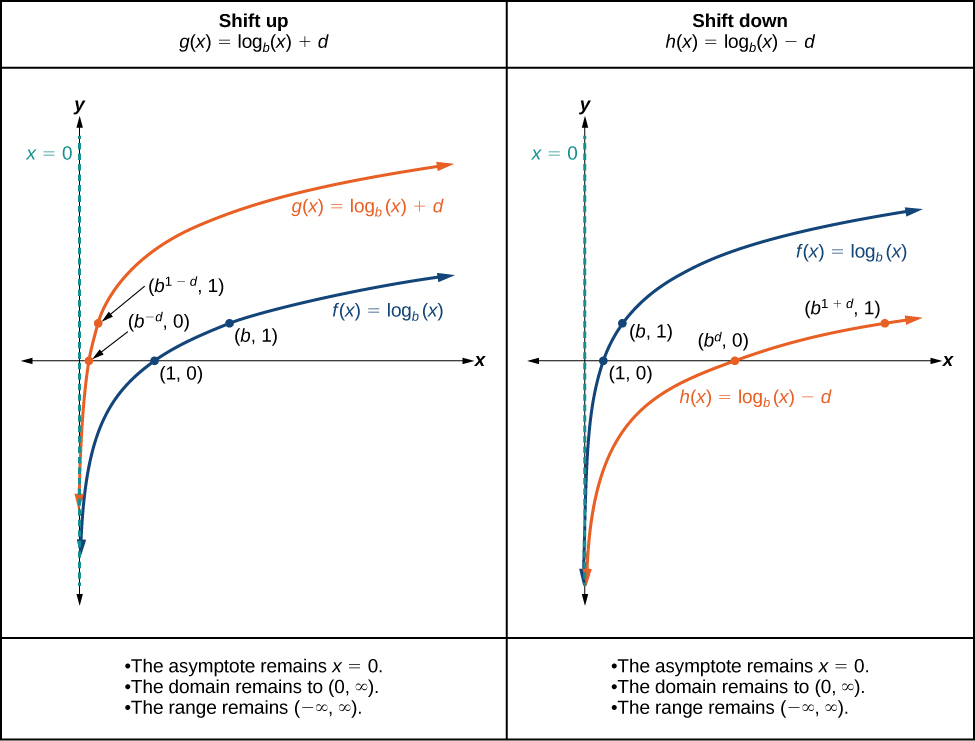
Sketch a graph of \(f(x)={\log}_3(x)−2\) alongside its basic function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Solution
Since the function is \(f(x)={\log}_3(x)−2\),we will notice \(d={ }–2\). Thus \(d<0\).
This means we will shift the function \(f(x)={\log}_3(x)\) down \(2\) units.
The vertical asymptote is \(x=0\).
Consider the three key points from the basic function, \(\left(\dfrac{1}{3},−1\right)\), \((1,0)\), and \((3,1)\).
The new coordinates are found by subtracting \(2\) from the y coordinates.
Label the points \(\left(\dfrac{1}{3},−3\right)\), \((1,−2)\), and \((3,−1)\).
The domain is \((0,\infty)\),the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).
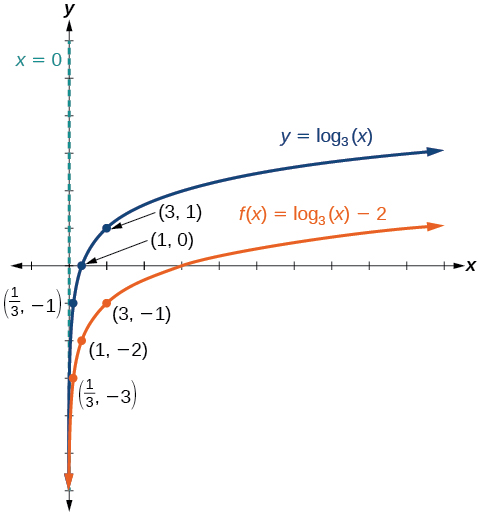
The domain is \((0,\infty)\),the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=0\).
Identify the transformations and use them to sketch the graph of \(L(x)=2+\log_3(x+1)\). State the domain, range, and asymptote.
Solution
We can rewrite \(L(x)=2+\log_3(x+1)\) as \(L(x)=\log_3(x+1)+2\) which can be helpful for identifying transformations.
The basic function is \(y=\log_3(x)\). The graph will shift left 1 unit and up 2 units.
Shifting left 1 unit and up 2 units results in the x-intercept of the basic graph shifting to \((0,2)\). The point \((3,1)\) on the basic graph shifts to \((2,3)\). The horizontal asymptote \(x=−1\).
Using these key points, asymptote, and the shape of \(y=\log_3(x)\), shift the whole graph left \(1\) units and down \(3\) units.
.png?revision=2&size=bestfit&width=404&height=402)
The domain is \((-1,\infty)\), the range is \((−\infty,\infty)\), and the horizontal asymptote is \(x=-1\)
Identify the transformations and use them to sketch the graph of \(m(x)=\log_5(x-4)-3\). State the domain, range, and asymptote.
- Answer
-
The transformations are shift right 4 units and shift down 3 units.
.png?revision=2&size=bestfit&width=447&height=443)
Figure \(\PageIndex{13}\): Graph of Transformed Logarithmic Function m(x) The domain is \((4,\infty)\), the range is \((−\infty,\infty)\), and the horizontal asymptote is \(x=4\)
Remember that the input for a logarithm is called the argument. When the argument is a single term, it is a common practice to not write parentheses. Example: \[f(x)={\log}_4(x)\text{ is equivalent to } f(x)={\log}_4x\nonumber\]
However, when the argument is more than one term, one must put parentheses around it. Example: \[y=\ln(x+3) \text{ is not equivalent to } y=\ln x+3\nonumber\]
The function on the left is a natural logarithmic function shifted left 3 units, whereas, the function on the right is a natural logarithmic function shifted up 3 units.
In graphing calculators, one needs to make sure functions are inputted properly also.
Graphing Reflections of \(f(x) = log_b(x)\)
When the basic function \(f(x)={\log}_b(x)\) is multiplied by \(−1\),the result is a reflection about the \(x\)-axis. When the input is multiplied by \(−1\),the result is a reflection about the \(y\)-axis. To visualize reflections, we restrict \(b>1\), and observe the general graph of the basic function \(f(x)={\log}_b(x)\) alongside the reflection about the \(x\)-axis, \(g(x)=−{\log}_b(x)\) and the reflection about the \(y\)-axis, \(h(x)={\log}_b(−x)\).
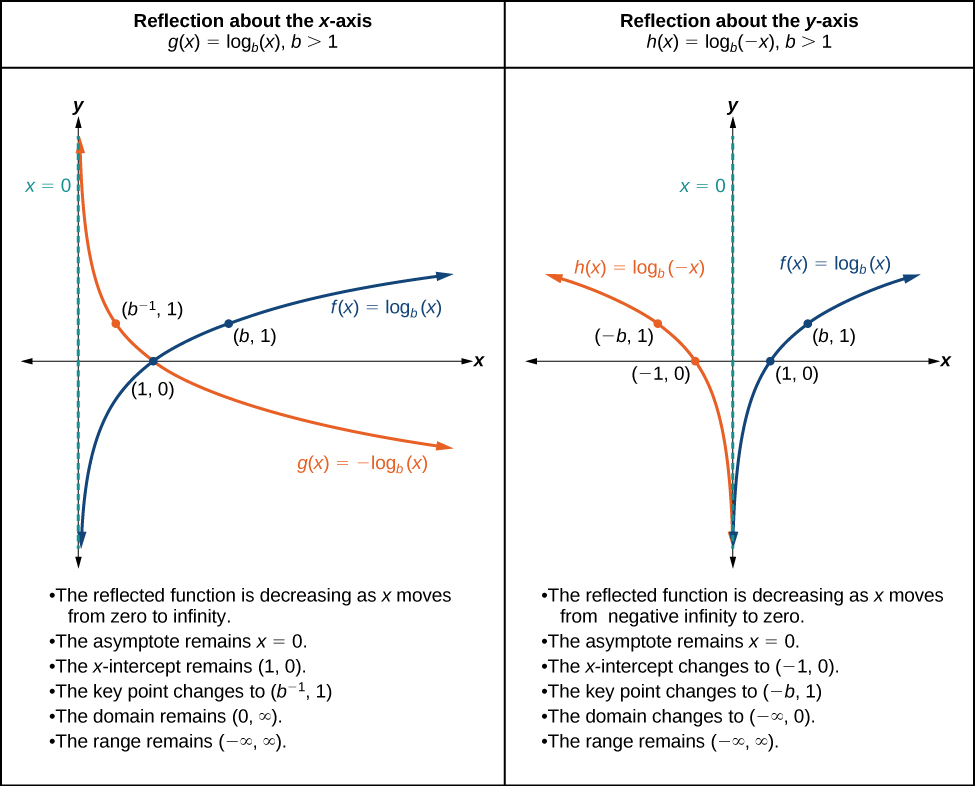
Sketch a graph of \(f(x)=\log(−x)\) alongside its basic function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Solution
Before graphing \(f(x)=log(−x)\), \(f(x)=log(−x)\),identify the behavior and key points for the graph.
- Since \(b=10\) is greater than one, we know that the basic function is increasing. Since the input value is multiplied by \(−1\), \(f(x)\) is a reflection of the basic graph about the \(y\)-axis. Thus, \(f(x)=\log(−x)\) will be decreasing as \(x\) moves from negative infinity to zero, and the right tail of the graph will approach the vertical asymptote \(x=0\).
- The \(x\)-intercept is \((−1,0)\).
- We draw and label the asymptote, plot and label the points, and draw a smooth curve through the points.
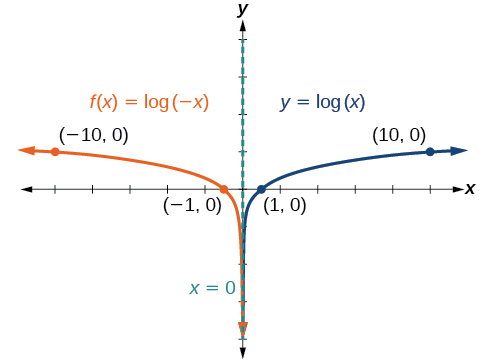
The domain is \((−\infty,0)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).
Graph \(f(x)=−\log(−x)\). State the domain, range, and asymptote.
- Answer
-
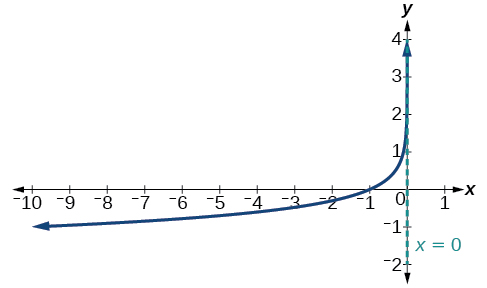
Figure \(\PageIndex{16}\) The domain is \((−\infty,0)\),the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=0\).
Graphing Stretches and Compressions of \(y = log_b(x)\)
When the basic function \(f(x)={\log}_b(x)\) is multiplied by a constant \(a>0\), the result is a vertical stretch or compression of the original graph. To visualize stretches and compressions, we set \(a>1\) and observe the general graph of the basic function \(f(x)={\log}_b(x)\) alongside the vertical stretch, \(g(x)=a{\log}_b(x)\) and the vertical compression, \(h(x)=\dfrac{1}{a}{\log}_b(x)\). See Figure \(\PageIndex{17}\).
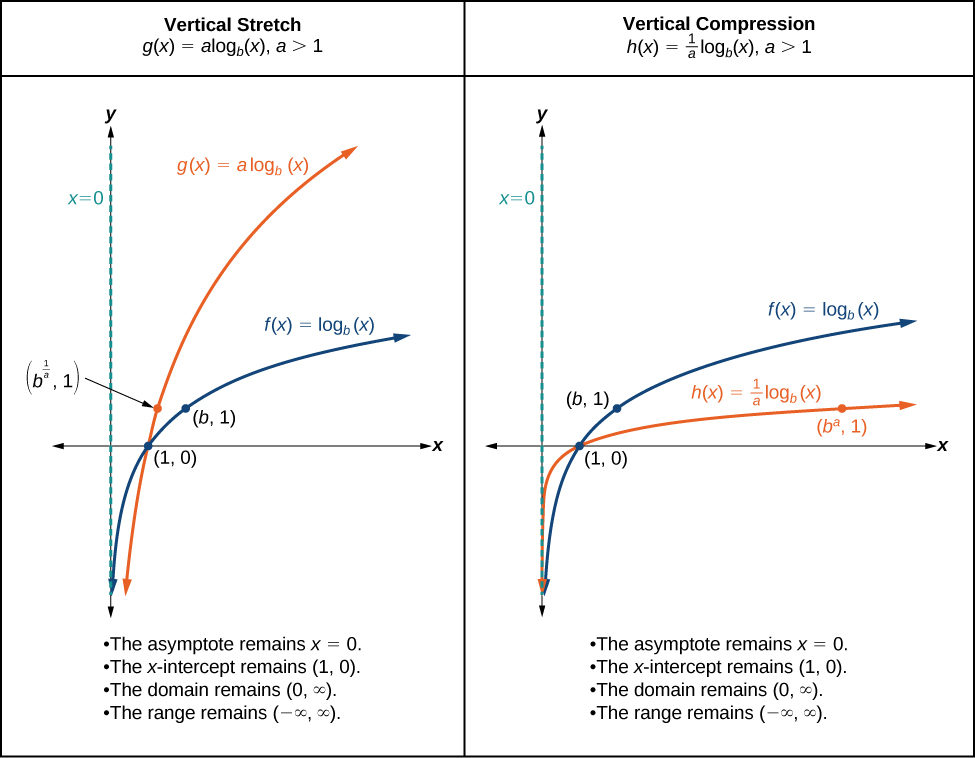
Sketch a graph of \(f(x)=2{\log}_4(x)\) alongside its basic function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Solution
Since the function is \(f(x)=2{\log}_4(x)\), we will notice \(a=2\).
This means we will stretch the function \(f(x)={\log}_4(x)\) by a factor of \(2\).
The vertical asymptote is \(x=0\).
Consider the three key points from the basic function, \(\left(\dfrac{1}{4},−1\right)\), \((1,0)\), and \((4,1)\).
The new coordinates are found by multiplying the \(y\) coordinates by \(2\).
Label the points \(\left(\dfrac{1}{4},−2\right)\), \((1,0)\), and \((4,2)\).
The domain is \((0, \infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\). See Figure \(\PageIndex{18}\).
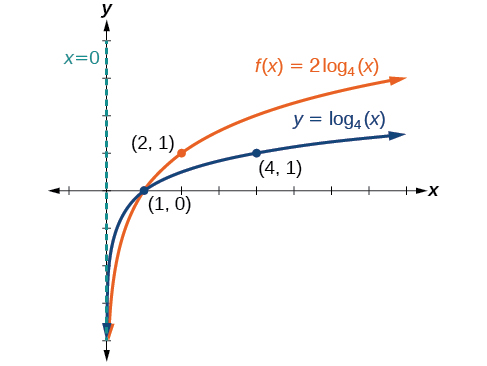
The domain is \((0,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=0\).
Sketch a graph of \(f(x)=5{\log}(x+2)\). State the domain, range, and asymptote.
Solution
Remember: what happens inside basicheses happens first. First, we move the graph left \(2\) units, then stretch the function vertically by a factor of \(5\), as in Figure \(\PageIndex{19}\). The vertical asymptote will be shifted to \(x=−2\). The \(x\)-intercept will be \((−1,0)\). The domain will be \((−2,\infty)\). Two points will help give the shape of the graph: \((−1,0)\) and \((8,5)\). We chose \(x=8\) as the x-coordinate of one point to graph because when \(x=8\), \(x+2=10\), the base of the common logarithm.
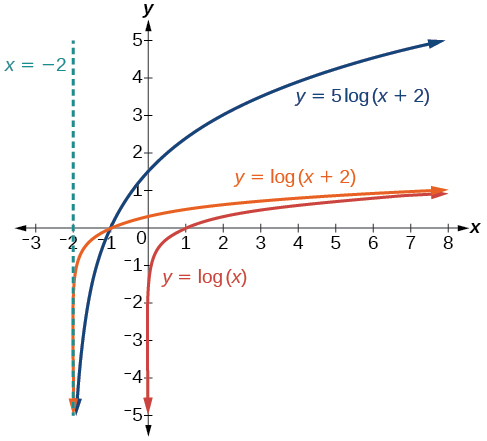
The domain is \((−2,\infty)\), the range is \((−\infty,\infty)\),and the vertical asymptote is \(x=−2\).
Sketch a graph of the function \(f(x)=3{\log}(x−2)+1\). State the domain, range, and asymptote.
- Answer
-
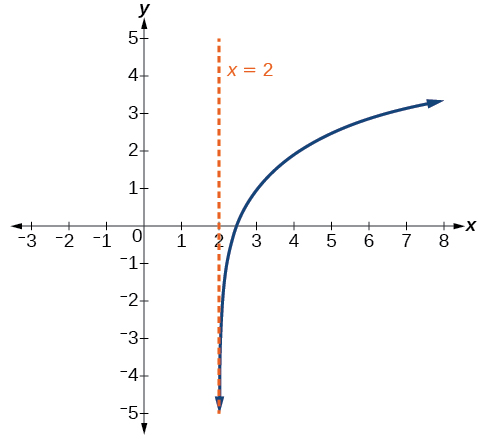
Figure \(\PageIndex{20}\) The domain is \((2,\infty)\), the range is \((−\infty,\infty)\), and the vertical asymptote is \(x=2\).
Summarizing Transformations of the Logarithmic Function
Now that we have worked with each type of transformation for the logarithmic function, we can summarize each to arrive at the general equation for translating exponential functions.
All transformations of the basic logarithmic function, \(y={\log}_b(x)\), have the form
\(f(x)=a{\log}_b(x+c)+d\)
where the basic function, \(y={\log}_b(x)\), \(b>1\),is
- shifted vertically up \(d\) units.
- shifted horizontally to the left \(c\) units.
- stretched vertically by a factor of \(|a|\) if \(|a|>0\).
- compressed vertically by a factor of \(|a|\) if \(0<|a|<1\).
- reflected about the x-axis when \(a<0\).
For \(f(x)=\log(−x)\), the graph of the basic function is reflected about the y-axis.
What is the vertical asymptote and domain of \(f(x)=−2{\log}_3(x+4)+5\)?
Solution
The vertical asymptote is at \(x=−4\).
Analysis
The coefficient, the base, and the upward transformation do not affect the asymptote. The shift of the curve \(4\) units to the left shifts the vertical asymptote to\(x=−4\). The domain is \((-4,\infty)\)
What is the vertical asymptote and domain of of \(f(x)=3+\ln(-x+1)\)?
- Answer
-
The vertical asymptote is \(x=1\). The domain is \((-\infty, 1)\)
Finding Equations of Logarithmic Functions that Model Graphical Information
Write an equation of the natural logarithmic function that has no vertical stretch or compression that is graphed in Figure \(\PageIndex{21}\).
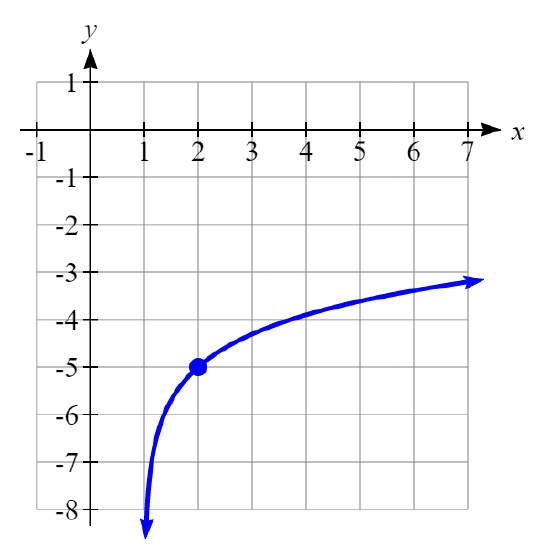
Solution
The vertical asymptote is at \(x=1\). There is a point at \((2,-5)\) that is one unit to the right of the asymptote which indicates this is the transformed x-intercept (remember that for basic functions that the vertical asymptote is at \(x=0\) and the x-intercept is at \((1,0)\)). This tells us the basic graph was shifted right 1 units and down 5 units. The equation for the graph is \(y=\ln(x-1)-5\)
Write an equation of the base 3 logarithmic function that is vertically stretched by 4, is reflected across the y-axis, and then shifted up 6 units.
- Answer
-
\(y=4\log_3(-x)+6\)


