5.5: Volume

Last updated
Save as PDF

Page ID: 57199

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Let’s revisit our friend Wally from “Area and Perimeter” and use another aspect of his yard to introduce the concept of volume. Wally is a swimmer and wants to install a lap pool in his backyard. Because he has some extra space, he is going to build a pool that is 25 yards long, 2 yards wide, and 2 yards deep. How many cubic yards of water must be used to fill the pool (assuming right to the top).

Much as we did with area (counting unit squares), with volume we will be counting unit cubes. What is the volume of a unit cube? Let’s look at figure 1:

Finding the Volume of a Cube

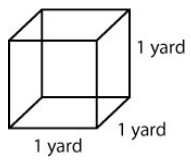
$Figure 1.$

Figure 1. Volume = 1 yd × 1yd × yd = 1 cubic yard

The shape at left is a cube (all sides are equal length). In particular, because all sides are of length 1, this cube is called a unit cube.

We know the area of the base from our previous work (1 yd × 1 yd or 1 square yard). We are going to take that area and extend it vertically through a height of 1 yard so our volume becomes

Volume = 1 yd × 1yd × yd = 1 cubic yard

How does this help Wally? Well, if he can count the number of unit cubes in his pool, he can determine the volume of water needed to fill the pool.

Guided Example

Filling Wally’s Pool

$Figure 2. Volume = Length× Width × Height or V = LWH$

Figure 2. Volume = Length × Width × Height or V = LWH

If we fill the pool with unit cubes, we can fill 25 unit cubes along the length, 2 along the width and 2 along the height. That would give us 25 × 2 × 2 = 100 unit cubes or:

Volume = 25 yd × 2 yd × 2 yd = 100 cubic yd

Explicit formulas for the types of rectangular solids used in the previous section are as follows:

Shape	Volume
Cub of side length L	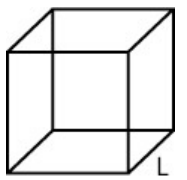$Fig2_4_3$	\(V=L \times L \times L \) \( V = L^3 \)
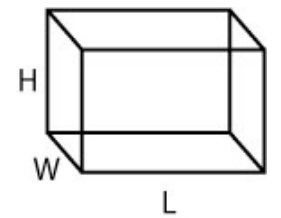Box with sides of length L, W, H	$Fig2_4_4$	\( V = L \times W \times H \)

Shape

Volume

Cub of side length L

$Fig2_4_3$

$V=L \times L \times L $

$ V = L^3 $

Box with sides of length L, W, H

$Fig2_4_4$

$ V = L \times W \times H $

Notes on Volume

Volume is a three-dimensional measurement that represents the amount of space inside a closed three-dimensional shape.
To find volume, count the number of unit cubes inside a given shape.
If there are units, include units in your final result. Units will always be three-dimensional (i.e. cubic feet, cubic yards, cubic miles, etc…)

Example 1

Find the volume of each shape below.

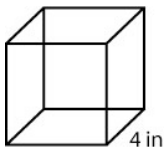
$Fig2_4_5$
A box with sides of length 2 ft, 3 ft, 2.5 ft.

Solutions

64 in³
15 ft³

Volume of A Circular Cylinder

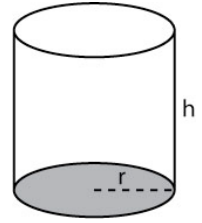
$Figure 3.$

Figure 3.

Can we use what we know about the area of a circle to formulate the volume of a can (also called a cylinder)? Take a look at figure 3.

The base circle is shaded. If we take the area of that circle ( $A = \pi r^2 $ ) and extend it up through the height h, then our volume for the can would be:

$V= \pi r^2 h$.

Example 2

Find the volume of the cylinder shown below.

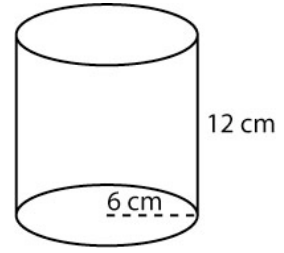
$Fig2_4_7$

Solution

432π cm³

Volume of Other Shapes

The chart below shows the volumes of some other basic geometric shapes.

Shape	Volume
Sphere	$V = \frac{4}{3} \pi r^3 $
Cone	$ V = \frac{1}{3} \pi r^2 h $
Pyramid	$ V = \frac{1}{3}LWH $

Example 3

Find the volume of a sphere with radius 5 meters.

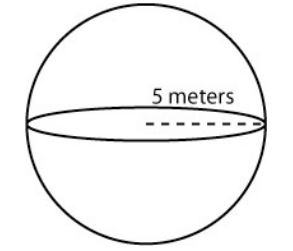
$Fig2_4_8$

Solution

$ \dfrac{500}{3} \text{cm}^3 $

Example 4

Determine the volume of each of the following. Include a drawing of the shape with the included information. Show all work. As in the examples, if units are included then units should be present in your final result. Use 3.14 for π and round answers to tenths as needed.

Find the volume of a cube with side 3.25 meters.
Find the volume of a box with sides of length 4 feet by 2.5 feet by 6 feet.
Find the volume of a can with radius 4.62 cm and height 10 cm.
Find the volume of a sphere with diameter 12 yards.

Solution

34.3 m³ or 34.3 cubic meters
60 ft³ or 60 cubic feet
670.2 cm³ or 670.2 cubic centimeters
904.3 yd³ or 904.3 cubic yards

Example 5

Applications of Volume

If you drank sodas from 5 cans each of diameter 4 inches and height 5 inches, how many cubic inches of soda did you drink? Use 3.14 for $ \pi $ and round to tenths.

Solution

314.0 in³(rounded)

Angles

Angles, often measured in degrees, measure the amount of rotation or “arc” between intersecting line segments. We need to have some sense of what an angle is before moving on to the next topic. See some examples and terminology below.

$Fig2_4_9$	This angle measures 30º This angle measure is less than 90º Angles less than 90º are called acute angles
$Fig2_4_10$	This angle measures 90º Angles that measure exactly 90º are called right angles The small box in the angle corner denotes a right angle
$Fig2_4_11$	This angle measures 120º This angle measure is more than 90º Angles that measure more than 90º but less 180º than are called obtuse angles
$Fig2_4_12$	This angle measures 180º Angles that measure exactly 180º are called straight angles

Basic Arithmetic Student Workbook. Authored by: Donna Gaudet, Amy Volpe, and Jenifer Bohart. Provided by: Scottsdale Community College. Located at: https://sccmath.wordpress.com/. License: CC BY-SA: Attribution-ShareAlike

Search

Text Color

Text Size

Margin Size

Font Type

Finding the Volume of a Cube

Guided Example

Filling Wally’s Pool

Notes on Volume

Example 1

Solutions

Example 2

Solution

Example 3

Solution

Example 4

Solution

Example 5

Applications of Volume

Solution

Shape	Volume
Sphere	\(V = \frac{4}{3} \pi r^3 \)
Cone	\( V = \frac{1}{3} \pi r^2 h \)
Pyramid	\( V = \frac{1}{3}LWH \)