3.6E: Exercises

Last updated

Jan 4, 2021
Save as PDF

Page ID: 54984

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Find an Equation of the Line Given the Slope and $y$ -Intercept

In the following exercises, find the equation of a line with given slope and $y$ -intercept. Write the equation in slope–intercept form.

Exercise $\PageIndex{1}$

slope $3$ and $y$ -intercept $(0,5)$

Exercise $\PageIndex{2}$

slope $4$ and $y$ -intercept $(0,1)$

Answer: $y=4x+1$

Exercise $\PageIndex{3}$

slope $6$ and $y$ -intercept $(0,−4)$

Exercise $\PageIndex{4}$

slope $8$ and $y$ -intercept $(0,−6)$

Answer: $y=8x−6$

Exercise $\PageIndex{5}$

slope $−1$ and $y$ -intercept $(0,3)$

Exercise $\PageIndex{6}$

slope $−1$ and $y$ -intercept $(0,7)$

Answer: $y=−x+7$

Exercise $\PageIndex{7}$

slope $−2$ and $y$ -intercept $(0,−3)$

Exercise $\PageIndex{8}$

slope $−3$ and $y$ -intercept $(0,−1)$

Answer: $y=−3x−1$

Exercise $\PageIndex{9}$

slope $\frac{3}{5}$ and $y$ -intercept $(0,-1)$

Exercise $\PageIndex{10}$

slope $\frac{1}{5}$ and $y$ -intercept $(0,-5)$

Answer: $y=\frac{1}{5} x-5$

Exercise $\PageIndex{11}$

slope $-\frac{3}{4}$ and $y$ -intercept $(0,-2)$

Exercise $\PageIndex{12}$

slope $-\frac{2}{3}$ and $y$ -intercept $(0,-3)$

Answer: $y=-\frac{2}{3} x-3$

Exercise $\PageIndex{13}$

slope $0$ and $y$ -intercept $(0,-1)$

Exercise $\PageIndex{14}$

slope $0$ and $y$ -intercept $(0,2)$

Answer: $y=2$

Exercise $\PageIndex{15}$

slope $-3$ and $y$ -intercept $(0,0)$

Exercise $\PageIndex{16}$

slope $-4$ and $y$ -intercept $(0,0)$

Answer: $y=−4x$

In the following exercises, find the equation of the line shown in each graph. Write the equation in slope–intercept form.

Exercise $\PageIndex{17}$

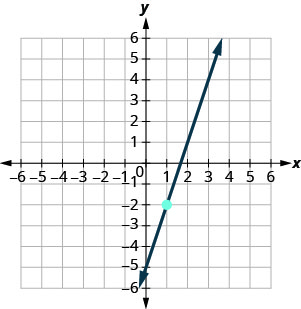
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (1, negative 2) is plotted. A line intercepts the y-axis at (0, negative 5), passes through the point (1, negative 2), and intercepts the x-axis at (5 thirds, 0).$

Exercise $\PageIndex{18}$

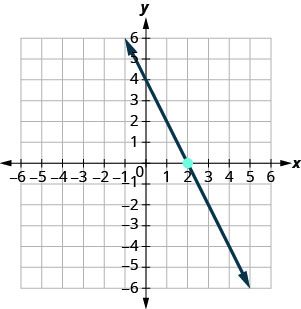
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (2, 0) is plotted. A line intercepts the y-axis at (0, 4) and intercepts the x-axis at (2, 0).$

Answer: $y=−2x+4$

Exercise $\PageIndex{19}$

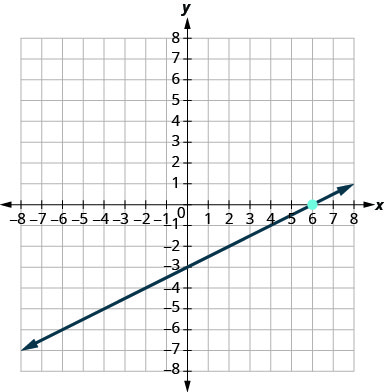
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (6, 0) is plotted. A line intercepts the y-axis at (0, negative 3) and intercepts the x-axis at (6, 0).$

Exercise $\PageIndex{20}$

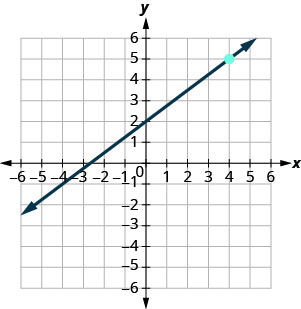
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (4, 5) is plotted. A line intercepts the x-axis at (negative 8 thirds, 0), intercepts the y-axis at (0, 2), and passes through the point (4, 5).$

Answer: $y=\frac{3}{4} x+2$

Exercise $\PageIndex{21}$

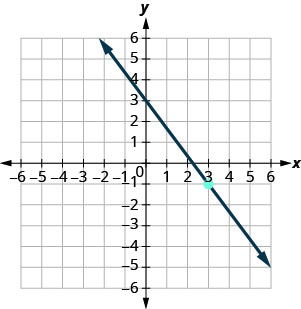
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (3, negative 1) is plotted. A line intercepts the y-axis at (0, 2), intercepts the x-axis at (9 fourths, 0), and passes through the point (3, negative 1).$

Exercise $\PageIndex{22}$

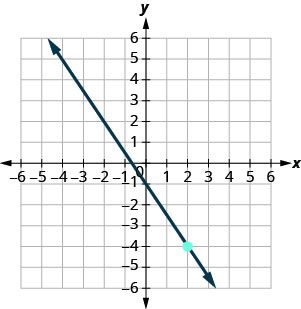
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (2, negative 4) is plotted. A line intercepts the x-axis at (negative 2 thirds, 0), intercepts the y-axis at (0, negative 1), and passes through the point (2, negative 4).$

Answer: $y=-\frac{3}{2} x-1$

Exercise $\PageIndex{23}$

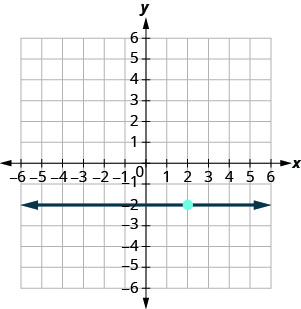
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (2, negative 2) is plotted. A line running parallel to the x-axis intercepts the y-axis at (0, negative 2) and passes through the point (2, negative 2).$

Exercise $\PageIndex{24}$

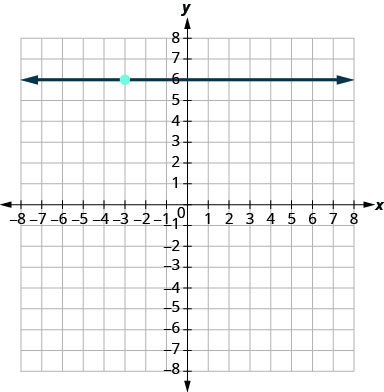
$The graph shows the x y-coordinate plane. The x and y-axes each run from negative 9 to 9. The point (negative 3, 6) is plotted. A line running parallel to the x-axis passes through (negative 3, 6) and intercepts the y-axis at (0, 6).$

Answer: $y=6$

Find an Equation of the Line Given the Slope and a Point

In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope–intercept form.

Exercise $\PageIndex{25}$

$m=\frac{5}{8},$ point $(8,3)$

Exercise $\PageIndex{26}$

$m=\frac{3}{8},$ point $(8,2)$

Answer: $y=\frac{3}{8} x-1$

Exercise $\PageIndex{27}$

$m=\frac{1}{6},$ point $(6,1)$

Exercise $\PageIndex{28}$

$m=\frac{5}{6},$ point $(6,7)$

Answer: $y=\frac{5}{6} x+2$

Exercise $\PageIndex{29}$

$m=-\frac{3}{4},$ point $(8,-5)$

Exercise $\PageIndex{30}$

$m=-\frac{3}{5},$ point $(10,-5)$

Answer: $y=-\frac{3}{5} x+1$

Exercise $\PageIndex{31}$

$m=-\frac{1}{4},$ point $(-12,-6)$

Exercise $\PageIndex{32}$

$m=-\frac{1}{3},$ point $(-9,-8)$

Answer: $y=-\frac{1}{3} x-11$

Exercise $\PageIndex{33}$

Horizontal line containing $(−2,5)$

Exercise $\PageIndex{34}$

Horizontal line containing $(−1,4)$

Answer: $y=4$

Exercise $\PageIndex{35}$

Horizontal line containing $(−2,−3)$

Exercise $\PageIndex{36}$

Horizontal line containing $(−1,−7)$

Answer: $y=−7$

Exercise $\PageIndex{37}$

$m=-\frac{3}{2},$ point $(-4,-3)$

Exercise $\PageIndex{38}$

$m=-\frac{5}{2},$ point $(-8,-2)$

Answer: $y=-\frac{5}{2} x-22$

Exercise $\PageIndex{39}$

$m=-7,$ point $(-1,-3)$

Exercise $\PageIndex{40}$

$m=-4,$ point $(-2,-3)$

Answer: $y=-4 x-11$

Exercise $\PageIndex{41}$

Horizontal line containing $(2,-3)$

Exercise $\PageIndex{42}$

Horizontal line containing $(4,-8)$

Answer: $y=−8$

Find an Equation of the Line Given Two Points

In the following exercises, find the equation of a line containing the given points. Write the equation in slope–intercept form.

Exercise $\PageIndex{43}$

$(2,6)$ and $(5,3)$

Exercise $\PageIndex{44}$

$(3,1)$ and $(2,5)$

Answer: $y=−4x+13$

Exercise $\PageIndex{45}$

$(4,3)$ and $(8,1)$

Exercise $\PageIndex{46}$

$(2,7)$ and $(3,8)$

Answer: $y=x+5$

Exercise $\PageIndex{47}$

$(−3,−4)$ and $(5,−2)$

Exercise $\PageIndex{48}$

$(−5,−3)$ and $(4,−6)$

Answer: $y=-\frac{1}{3} x-\frac{14}{3}$

Exercise $\PageIndex{49}$

$(−1,3)$ and $(−6,−7)$

Exercise $\PageIndex{50}$

$(−2,8)$ and $(−4,−6)$

Answer: $y=7x+22$

Exercise $\PageIndex{51}$

$(6,−4)$ and $(−2,5)$

Exercise $\PageIndex{52}$

$(3,−2)$ and $(−4,4)$

Answer: $y=-\frac{6}{7} x+\frac{4}{7}$

Exercise $\PageIndex{53}$

$(0,4)$ and $(2,−3)$

Exercise $\PageIndex{54}$

$(0,−2)$ and $(−5,−3)$

Answer: $y=\frac{1}{5} x-2$

Exercise $\PageIndex{55}$

$(7,2)$ and $(7,−2)$

Exercise $\PageIndex{56}$

$(4,2)$ and $(4,−3)$

Answer: $x=4$

Exercise $\PageIndex{57}$

$(−7,−1)$ and $(−7,−4)$

Exercise $\PageIndex{58}$

$(−2,1)$ and $(−2,−4)$

Answer: $x=−2$

Exercise $\PageIndex{59}$

$(6,1)$ and $(0,1)$

Exercise $\PageIndex{60}$

$(6,2)$ and $(−3,2)$

Answer: $y=2$

Exercise $\PageIndex{61}$

$(3,−4)$ and $(5,−4)$

Exercise $\PageIndex{62}$

$(−6,−3)$ and $(−1,−3)$

Answer: $y=−3$

Exercise $\PageIndex{63}$

$(4,3)$ and $(8,0)$

Exercise $\PageIndex{64}$

$(0,0)$ and $(1,4)$

Answer: $y=4x$

Exercise $\PageIndex{65}$

$(−2,−3)$ and $(−5,−6)$

Exercise $\PageIndex{66}$

$(−3,0)$ and $(−7,−2)$

Answer: $y=\frac{1}{2} x+\frac{3}{2}$

Exercise $\PageIndex{67}$

$(8,−1)$ and $(8,−5)$

Exercise $\PageIndex{68}$

$(3,5)$ and $(−7,5)$

Answer: $y=5$

Find an Equation of a Line Parallel to a Given Line

In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope–intercept form.

Exercise $\PageIndex{69}$

line $y=4 x+2,$ point $(1,2)$

Exercise $\PageIndex{70}$

line $y=3 x+4,$ point $(2,5)$

Answer: $y=3 x-1$

Exercise $\PageIndex{71}$

line $y=-2 x-3,$ point $(-1,3)$

Exercise $\PageIndex{72}$

line $y=-3x-1,$ point $(2,-3)$

Answer: $y=−3x+3$

Exercise $\PageIndex{73}$

line $3 x-y=4,$ point $(3,1)$

Exercise $\PageIndex{74}$

line $2 x-y=6,$ point $(3,0)$

Answer: $y=2x−6$

Exercise $\PageIndex{75}$

line $4 x+3 y=6,$ point $(0,-3)$

Exercise $\PageIndex{76}$

line $2x+3y=6,$ point $(0,5)$

Answer: $y=-\frac{2}{3} x+5$

Exercise $\PageIndex{77}$

line $x=-3,$ point $(-2,-1)$

Exercise $\PageIndex{78}$

line $x=-4,$ point $(-3,-5)$

Answer: $x=−3$

Exercise $\PageIndex{79}$

line $x-2=0,$ point $(1,-2)$

Exercise $\PageIndex{80}$

line $x-6=0,$ point $(4,-3)$

Answer: $x=4$

Exercise $\PageIndex{81}$

line $y=5,$ point $(2,-2)$

Exercise $\PageIndex{82}$

line $y=1,$ point $(3,-4)$

Answer: $y=−4$

Exercise $\PageIndex{83}$

line $y+2=0,$ point $(3,-3)$

Exercise $\PageIndex{84}$

line $y+7=0,$ point $(1,-1)$

Answer: $y=−1$

Find an Equation of a Line Perpendicular to a Given Line

In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope–intercept form.

Exercise $\PageIndex{85}$

line $y=-2 x+3,$ point $(2,2)$

Exercise $\PageIndex{86}$

line $y=-x+5,$ point $(3,3)$

Answer: $y=x$

Exercise $\PageIndex{87}$

line $y=\frac{3}{4} x-2,$ point $(-3,4)$

Exercise $\PageIndex{88}$

line $y=\frac{2}{3} x-4,$ point $(2,-4)$

Answer: $y=-\frac{3}{2} x-1$

Exercise $\PageIndex{89}$

line $2 x-3 y=8,$ point $(4,-1)$

Exercise $\PageIndex{90}$

line $4 x-3 y=5,$ point $(-3,2)$

Answer: $y=-\frac{3}{4} x-\frac{1}{4}$

Exercise $\PageIndex{91}$

line $2 x+5 y=6,$ point $(0,0)$

Exercise $\PageIndex{92}$

line $4 x+5 y=-3,$ point $(0,0)$

Answer: $y=\frac{5}{4} x$

Exercise $\PageIndex{93}$

line $y-3=0,$ point $(-2,-4)$

Exercise $\PageIndex{94}$

line $y-6=0,$ point $(-5,-3)$

Answer: $x=-5$

Exercise $\PageIndex{95}$

line $y$ -axis, point $(3,4)$

Exercise $\PageIndex{96}$

line $y$ -axis, point $(2,1)$

Answer: $y=1$

Mixed Practice

In the following exercises, find the equation of each line. Write the equation in slope–intercept form.

Exercise $\PageIndex{97}$

Containing the points $(4,3)$ and $(8,1)$

Exercise $\PageIndex{98}$

Containing the points $(2,7)$ and $(3,8)$

Answer: $y=x+5$

Exercise $\PageIndex{99}$

$m=\frac{1}{6},$ containing point $(6,1)$

Exercise $\PageIndex{100}$

$m=\frac{5}{6},$ containing point $(6,7)$

Answer: $y=\frac{5}{6} x+2$

Exercise $\PageIndex{101}$

Parallel to the line $4 x+3 y=6,$ containing point $(0,-3)$

Exercise $\PageIndex{102}$

Parallel to the line $2 x+3 y=6,$ containing point $(0,5)$

Answer: $y=-\frac{2}{3} x+5$

Exercise $\PageIndex{103}$

$m=-\frac{3}{4},$ containing point $(8,-5)$

Exercise $\PageIndex{104}$

$m=-\frac{3}{5},$ containing point $(10,-5)$

Answer: $y=-\frac{3}{5} x+1$

Exercise $\PageIndex{105}$

Perpendicular to the line $y-1=0,$ point $(-2,6)$

Exercise $\PageIndex{106}$

Perpendicular to the line y-axis, point $(-6,2)$

Answer: $y=2$

Exercise $\PageIndex{107}$

Containing the points $(4,3)$ and $(8,1)$

Exercise $\PageIndex{108}$

Containing the points $(-2,0)$ and $(-3,-2)$

Answer: $y=x+2$

Exercise $\PageIndex{109}$

Parallel to the line $x=-3,$ containing point $(-2,-1)$

Exercise $\PageIndex{110}$

Parallel to the line $x=-4,$ containing point $(-3,-5)$

Answer: $x=-3$

Exercise $\PageIndex{111}$

Containing the points $(-3,-4)$ and $(2,-5)$

Exercise $\PageIndex{112}$

Containing the points $(-5,-3)$ and $(4,-6)$

Answer: $y=-\frac{1}{3} x-\frac{14}{3}$

Exercise $\PageIndex{113}$

Perpendicular to the line $x-2 y=5,$ containing point $(-2,2)$

Exercise $\PageIndex{114}$

Perpendicular to the line $4 x+3 y=1,$ containing point $(0,0)$

Answer: $y=\frac{3}{4} x$

Everyday Math

Exercise $\PageIndex{115}$

Cholesterol. The age, $x,$ and LDL cholesterol evel, $y,$ of two men are given by the points $(18,68)$ and $(27,122) .$ Find a linear equation that models the relationship between age and LDL cholesterol level.

Exercise $\PageIndex{116}$

Fuel consumption. The city mpg, $x$ , and highway mpg, $y,$ of two cars are given by the points $(29,40)$ and $(19,28) .$ Find a
linear equation that models the relationship between city mpg and highway mpg.

Answer: $y=1.2 x+5.2$

Writing Exercises

Exercise $\PageIndex{117}$

Why are all horizontal lines parallel?

Exercise $\PageIndex{118}$

Explain in your own words why the slopes of two perpendicular lines must have opposite signs.

Answer: Answers will vary.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This is a table that has six rows and four columns. In the first row, which is a header row, the cells read from left to right: “I can…,” “confidently,” “with some help,” and “no-I don’t get it!” The first column below “I can…” reads “find the equation of the line given the slope and y-intercept,”, “find an equation of the line given the slope and a point,” “find an equation of the line given two points,” “find an equation of a line parallel to a given line,” and “find an equation of a line perpendicular to a given line.” The rest of the cells are blank.$

b. On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Practice Makes Perfect

Exercise 3.6E.1\PageIndex{1}

Exercise 3.6E.2\PageIndex{2}

Exercise 3.6E.3\PageIndex{3}

Exercise 3.6E.4\PageIndex{4}

Exercise 3.6E.5\PageIndex{5}

Exercise 3.6E.6\PageIndex{6}

Exercise 3.6E.7\PageIndex{7}

Exercise 3.6E.8\PageIndex{8}

Exercise 3.6E.9\PageIndex{9}

Exercise 3.6E.10\PageIndex{10}

Exercise 3.6E.11\PageIndex{11}

Exercise 3.6E.12\PageIndex{12}

Exercise 3.6E.13\PageIndex{13}

Exercise 3.6E.14\PageIndex{14}

Exercise 3.6E.15\PageIndex{15}

Exercise 3.6E.16\PageIndex{16}

Exercise 3.6E.17\PageIndex{17}

Exercise 3.6E.18\PageIndex{18}

Exercise 3.6E.19\PageIndex{19}

Exercise 3.6E.20\PageIndex{20}

Exercise 3.6E.21\PageIndex{21}

Exercise 3.6E.22\PageIndex{22}

Exercise 3.6E.23\PageIndex{23}

Exercise 3.6E.24\PageIndex{24}

Exercise 3.6E.25\PageIndex{25}

Exercise 3.6E.26\PageIndex{26}

Exercise 3.6E.27\PageIndex{27}

Exercise 3.6E.28\PageIndex{28}

Exercise 3.6E.29\PageIndex{29}

Exercise 3.6E.30\PageIndex{30}

Exercise 3.6E.31\PageIndex{31}

Exercise 3.6E.32\PageIndex{32}

Exercise 3.6E.33\PageIndex{33}

Exercise 3.6E.34\PageIndex{34}

Exercise 3.6E.35\PageIndex{35}

Exercise 3.6E.36\PageIndex{36}

Exercise 3.6E.37\PageIndex{37}

Exercise 3.6E.38\PageIndex{38}

Exercise 3.6E.39\PageIndex{39}

Exercise 3.6E.40\PageIndex{40}

Exercise 3.6E.41\PageIndex{41}

Exercise 3.6E.42\PageIndex{42}

Exercise 3.6E.43\PageIndex{43}

Exercise 3.6E.44\PageIndex{44}

Exercise 3.6E.45\PageIndex{45}

Exercise 3.6E.46\PageIndex{46}

Exercise 3.6E.47\PageIndex{47}

Exercise 3.6E.48\PageIndex{48}

Exercise 3.6E.49\PageIndex{49}

Exercise 3.6E.50\PageIndex{50}

Exercise 3.6E.51\PageIndex{51}

Exercise 3.6E.52\PageIndex{52}

Exercise 3.6E.53\PageIndex{53}

Exercise 3.6E.54\PageIndex{54}

Exercise 3.6E.55\PageIndex{55}

Exercise 3.6E.56\PageIndex{56}

Exercise 3.6E.57\PageIndex{57}

Exercise 3.6E.58\PageIndex{58}

Exercise 3.6E.59\PageIndex{59}

Exercise 3.6E.60\PageIndex{60}

Exercise 3.6E.61\PageIndex{61}

Exercise 3.6E.62\PageIndex{62}

Exercise 3.6E.63\PageIndex{63}

Exercise 3.6E.64\PageIndex{64}

Exercise 3.6E.65\PageIndex{65}

Exercise 3.6E.66\PageIndex{66}

Exercise 3.6E.67\PageIndex{67}

Exercise 3.6E.68\PageIndex{68}

Exercise 3.6E.69\PageIndex{69}

Exercise 3.6E.70\PageIndex{70}

Exercise 3.6E.71\PageIndex{71}

Exercise 3.6E.72\PageIndex{72}

Exercise 3.6E.73\PageIndex{73}

Exercise 3.6E.74\PageIndex{74}

Exercise 3.6E.75\PageIndex{75}

Exercise 3.6E.76\PageIndex{76}

Exercise 3.6E.77\PageIndex{77}

Exercise 3.6E.78\PageIndex{78}

Exercise 3.6E.79\PageIndex{79}