5.2: Logarithmic Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
A population of 50 flies is expected to double every week, leading to a function of the form f(x)=50(2)x, where x represents the number of weeks that have passed. When will this population reach 500? Trying to solve this problem leads to:
500=50(2)x Dividing both sides by 50 to isolate the exponential
10=2x
While we have set up exponential models and used them to make predictions, you may have noticed that solving exponential equations has not yet been mentioned. The reason is simple: none of the algebraic tools discussed so far are sufficient to solve exponential equations. Consider the equation 2x=10 above. We know that 23=8 and 24=16, so it is clear that x must be some value between 3 and 4 since g(x)=2x is increasing. We could use technology to create a table of values or graph to better estimate the solution.

From the graph, we could better estimate the solution to be around 3.3. This result is still fairly unsatisfactory, and since the exponential function is one-to-one, it would be great to have an inverse function. None of the functions we have already discussed would serve as an inverse function and so we must introduce a new function, named log as the inverse of an exponential function. Since exponential functions have different bases, we will define corresponding logarithms of different bases as well.
Definition: logarithm
The logarithm (base b) function, written logb(x), is the inverse of the exponential function (base b), bx.
Since the logarithm and exponential “undo” each other (in technical terms, they are inverses), it follows that:
properties of logs: inverse properties
logb(bx)=x
blogbx=x
Since log is a function, it is most correctly written as \boldsymbol{\log _b}(c)}, using parentheses to denote function evaluation, just as we would with f(c). However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written as logbc.
logarithm equivalent to an exponential
The statement ba=c is equivalent to the statement logb(c)=a.
Alternatively, we could show this by starting with the exponential functionc=ba, then taking the log base b of both sides, giving logb(c)=logbba. Using the inverse property of logs, we see that logb(c)=a.
Since log is a function, it is most correctly written as logb(c), using parentheses to denote function evaluation, just as we would with f(c). However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written as logbc.
Example 5.2.1
Write these exponential equations as logarithmic equations:
- 23=8
- 52=25
- 10−4=110000
Solution
a) 23=8 is equivalent to log2(8)=3
b) 52=25 is equivalent to log5(25)=2
c) 10−4=110000 is equivalent to log10(110000)=−4
Example 5.2.2
Write these logarithmic equations as exponential equations:
a) log6(√6)=12 b) log3(9)=2
Solution
a) log6(√6)=12 is equivalent to 61/2=√6
b) log3(9)=2 is equivalent to 32=9
Exercise 5.2.1
Write the exponential equation 42=16 as a logarithmic equation.
- Answer
-
log4(16)=2=log442=2log44
By establishing the relationship between exponential and logarithmic functions, we can now solve basic logarithmic and exponential equations by rewriting.
Example 5.2.3
Solve log4(x)=2 for x.
Solution
By rewriting this expression as an exponential, 42=x, so x=16.
Example 5.2.4
Solve 2x=10 for x.
Solution
By rewriting this expression as a logarithm, we get x=log2(10).
While this does define a solution, and an exact solution at that, you may find it somewhat unsatisfying since it is difficult to compare this expression to the decimal estimate we made earlier. Also, giving an exact expression for a solution is not always useful – often we really need a decimal approximation to the solution. Luckily, this is a task calculators and computers are quite adept at. Unluckily for us, most calculators and computers will only evaluate logarithms of two bases. Happily, this ends up not being a problem, as we will see briefly.
Definition: common and natural logarithms
The common log is the logarithm with base 10, and is typically written log(x).
The natural log is the logarithm with base e, and is typically written ln(x).
Example 5.2.5
Evaluate log(1000) using the definition of the common log.
| number | number as exponential | log(number) |
|---|---|---|
| 1000 | 103 | 3 |
| 100 | 102 | 2 |
| 10 | 101 | 1 |
| 1 | 100 | 0 |
| 0.1 | 10−1 | -1 |
| 0.01 | 10−2 | -2 |
| 0.001 | 10−3 | -3 |
Solution
To evaluate log(1000), we can let x=log(1000), then rewrite into exponential form using the common log base of 10:
10x=1000.
From this, we might recognize that 1000 is the cube of 10, so x = 3.
We also can use the inverse property of logs to write log10(103)=3.
Exercise 5.2.2
Evaluate log(1,000,000).
- Answer
-
log(1000000)=log(106)=6
Example 5.2.6
Evaluate ln(√e).
Solution
We can rewrite ln(√e) as ln(e1/2). Since ln is a log base e, we can use the inverse property for logs: ln(e1/2)=loge(e1/2)=12.
Example 5.2.7
Evaluate log(500) using your calculator or computer.
Solution
Using a computer, we can evaluate log(500)≈2.69897
Graphs of Logarithms
Recall that the exponential function f(x)=2x produces this table of values
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|---|---|---|---|---|---|---|---|
|
f(x) |
18 |
14 |
12 |
1 |
2 |
4 |
8 |
Since the logarithmic function “undoes” the exponential, g(x)=log2(x) produces the table of values
|
x |
18 |
14 |
12 |
1 |
2 |
4 |
8 |
|---|---|---|---|---|---|---|---|
|
g(x) |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
In this second table, notice that
- As the input increases, the output increases.
- As input increases, the output increases more slowly.
- Since the exponential function only outputs positive values, the logarithm can only accept positive values as inputs, so the domain of the log function is (0,∞).
- Since the exponential function can accept all real numbers as inputs, the logarithm can output any real number, so the range is all real numbers or (−∞,∞).
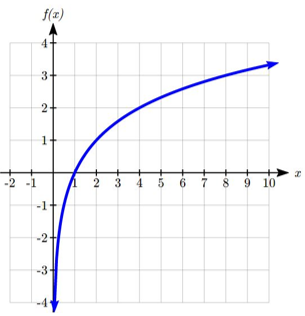
Sketching the graph, notice that as the input approaches zero from the right, the output of the function grows very large in the negative direction, indicating a vertical asymptote at x=0.
In symbolic notation we write:
as x→0+,f(x)→−∞, and as x→∞,f(x)→∞.
Graphical Features of the Logarithm
Graphically, in the function g(x)=logb(x):
The graph has a horizontal intercept at (1, 0);
The graph has a vertical asymptote at x=0;
The graph is increasing and concave down;
The domain of the function is x>0, or (0,∞);
The range of the function is all real numbers, or (−∞,∞).
When sketching a general logarithm with base b, it can be helpful to remember that the graph will pass through the points (1,0) and (b,1).
To get a feeling for how the base affects the shape of the graph, examine the graphs below.

Notice that the larger the base, the slower the graph grows. For example, the common log graph, while it grows without bound, it does so very slowly. For example, to reach an output of 8, the input must be 100,000,000.
Another important observation made was the domain of the logarithm. Like the reciprocal and square root functions, the logarithm has a restricted domain which must be considered when finding the domain of a composition involving a log.
Example 5.2.8
Find the domain of the function f(x)=log(5−2x).
Solution
The logarithm is only defined with the input is positive, so this function will only be defined when 5−2x>0. Solving this inequality,
−2x>−5x<52
The domain of this function is x<52, or in interval notation, (−∞,52).
Logarithm Properties
To utilize the common or natural logarithm functions to evaluate expressions like log2(10), we need to establish some additional properties.
properties of logs: exponent property
logb(Ar)=rlogb(A)
To show why this is true, we offer a proof:
Since the logarithmic and exponential functions are inverses, blogbA=A.
Raising both sides to the r power, we get Ar=(blogbA)r.
Utilizing the exponential rule that states(xp)q=xpq, Ar=(blogbA)r=brlogbA
Taking the log of both sides, logb(Ar)=logb(brlogbA)
Utilizing the inverse property on the right side yields the result: logb(Ar)=rlogbA
Example 5.2.9
Rewrite log3(25) using the exponent property for logs.
Solution
Since 25 = 52,
log3(25)=log3(52)=2log3(5)
Example 5.2.10
Rewrite 4ln(x)using the exponent property for logs.
Solution
Using the property in reverse, 4ln(x)=ln(x4).
Exercise 5.2.3
Rewrite using the exponent property for logs: ln(1x2).
- Answer
-
3.ln(1x2)=ln(x−2)=−2ln(x)
The exponent property allows us to find a method for changing the base of a logarithmic expression.
properties of logs: change of base
logb(A)=logc(A)logc(b)
Proof
Let logb(A)=x.
Rewriting as an exponential gives bx=A.
Taking the log base c of both sides of this equation gives
logcbx=logcA
Now utilizing the exponent property for logs on the left side,
xlogcb=logcA
Dividing, we obtain x=logcAlogcb. Replacing our original expression for x,
logbA=logcAlogcb
With this change of base formula, we can finally find a good decimal approximation to our question from the beginning of the section.
Example 5.2.11
Evaluate log2(10) using the change of base formula.
Solution
According to the change of base formula, we can rewrite the log base 2 as a logarithm of any other base. Since our calculators can evaluate the natural log, we might choose to use the natural logarithm, which is the log base e:
log210=loge10loge2=ln10ln2
Using our calculators to evaluate this,
ln10ln2≈2.302590.69315≈3.3219
This finally allows us to answer our original question – the population of flies we discussed at the beginning of the section will take 3.32 weeks to grow to 500.
Example 5.2.12
Evaluate log5(100) using the change of base formula.
Solution
We can rewrite this expression using any other base. If our calculators are able to evaluate the common logarithm, we could rewrite using the common log, base 10.
log5(100)=log10100log105≈20.69897=2.861
While we can solve the basic exponential equation 2x=10 by rewriting in logarithmic form and then using the change of base formula to evaluate the logarithm, the proof of the change of base formula illuminates an alternative approach to solving exponential equations.
Solving Exponential Equations
- Isolate the exponential expressions when possible
- Take the logarithm of both sides
- Utilize the exponent property for logarithms to pull the variable out of the exponent
- Use algebra to solve for the variable.
Example 5.2.13
Solve 2x=10 for x.
Solution
Using this alternative approach, rather than rewrite this exponential into logarithmic form, we will take the logarithm of both sides of the equation. Since we often wish to evaluate the result to a decimal answer, we will usually utilize either the common log or natural log. For this example, we’ll use the natural log:
ln(2x)=ln(10) Utilizing the exponent property for logs,
xln(2)=ln(10) Now dividing by ln(2),
x=ln(10)ln(2)≈3.3219
Notice that this result matches the result we found using the change of base formula.
Example 5.2.14
In the first section, we predicted the population (in billions) of India t years after 2008 by using the function f(t)=1.14(1+0.0134)t. If the population continues following this trend, when will the population reach 2 billion?
Solution
We need to solve for time t so that f(t)=2.
2=1.14(1.0134)t Divide by 1.14 to isolate the exponential expression
21.14=1.0134t Take the logarithm of both sides of the equation
ln(21.14)=ln(1.0134t) Apply the exponent property on the right side
ln(21.14)=tln(1.0134) Divide both sides by ln(1.0134)
t=ln(21.14)ln(1.0134)≈42.23 years
If this growth rate continues, the model predicts the population of India will reach 2 billion about 42 years after 2008, or approximately in the year 2050.
Exercise 5.2.4
Solve 5(0.93)x=10.
- Answer
-
5(0.93)x=10(0.93)x=2ln(0.93x)=ln(2)xln(0.93)=ln(2)ln(2)ln(0.93)≈−9.5513
Example 5.2.14
Solve 5(1.07)3t=2
Solution
To start, we want to isolate the exponential part of the expression, the (1.07)3t, so it is alone on one side of the equation. Then we can use the log to solve the equation. We can use any base log; this time we’ll use the common log.
5(1.07)3t=2 Divide both sides by 5 to isolate the exponential
(1.07)3t=25 Take the log of both sides.
log((1.07)3t)=log(25) Use the exponent property for logs
3tlog(1.07)=log(25) Divide by 3log(1.07) on both sides
3tlog(1.07)3log(1.07)=log(25)3log(1.07) Simplify and evaluate
t=log(25)3log(1.07)≈−4.5143
Note that when entering that expression on your calculator, be sure to put parentheses around the whole denominator to ensure the proper order of operations:
log(2/5)/(3*log(1.07))
Additional Properties of Logarithms
Some situations cannot be addressed using the properties already discussed. For these, we need some additional properties.
properties of logs
Sum of Logs Property:
logb(A)+logb(C)=logb(AC)
Difference of Logs Property:
logb(A)−logb(C)=logb(AC)
It’s just as important to know what properties logarithms do not satisfy as to memorize the valid properties listed above. In particular, the logarithm is not a linear function, which means that it does not distribute:
logA+B≠logA+logB.
With these properties, we can rewrite expressions involving multiple logs as a single log, or break an expression involving a single log into expressions involving multiple logs.
Example 5.2.15
Write log3(5)+log3(8)−log3(2) as a single logarithm.
Solution
Using the sum of logs property on the first two terms,
log3(5)+log3(8)=log3(5⋅8)=log3(40)
This reduces our original expression to
log3(40)−log3(2)
Then using the difference of logs property,
log3(40)−log3(2)=log3(402)=log3(20)
Example 5.2.16
Evaluate 2log(5)+log(4) without a calculator by first rewriting as a single logarithm.
Solution
On the first term, we can use the exponent property of logs to write
2log(5)=log(52)=log(25)
With the expression reduced to a sum of two logs, log(25)+log(4), we can utilize the sum of logs property
log(25)+log(4)=log(4⋅25)=log(100)
Since 100=102, we can evaluate this log without a calculator:
log(100)=log(102)=2
Example 5.2.17
Rewrite ln(x4y7) as a sum or difference of logs
Solution
First, noticing we have a quotient of two expressions, we can utilize the difference property of logs to write
ln(x4y7)=ln(x4y)−ln(7)
Then seeing the product in the first term, we use the sum property
ln(x4y)−ln(7)=ln(x4)+ln(y)−ln(7)
Finally, we could use the exponent property on the first term
ln(x4)+ln(y)−ln(7)=4ln(x)+ln(y)−ln(7)
Log properties in solving equations
The logarithm properties often arise when solving problems involving logarithms.
Example 5.2.18
Solve log(50x+25)−log(x)=2.
Solution
In order to rewrite in exponential form, we need a single logarithmic expression on the left side of the equation. Using the difference property of logs, we can rewrite the left side:
log(50x+25x)=2
Rewriting in exponential form reduces this to an algebraic equation:
50x+25x=102=100 Multiply both sides by x
50x+25=100x Combine like terms
25=50x Divide by 50
x=2550=12
Checking this answer in the original equation, we can verify there are no domain issues, and this answer is correct.
Exercise 5.2.6
Solve log(x2−4)=1+log(x+2).
- Answer
-
12
Important Topics of this Section
- The Logarithmic function as the inverse of the exponential function
- Writing logarithmic & exponential expressions
- Properties of logs
- Inverse properties
- Exponential properties
- Change of base
- Sum and difference of logs properties
- Common log
- Natural log
- Graph of the logarithmic function (domain and range)
- Solving exponential equations
- Solving equations using log rules


