6.E: Triangles and Vectors (Exercises)

Last updated
Save as PDF

Page ID: 69174

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Vector (Exercises)

Verbal

1) What are the characteristics of the letters that are commonly used to represent vectors?

Answer: lowercase, bold letter, usually $u, v, w$

2) How is a vector more specific than a line segment?

3) What are $i$ and $j$, and what do they represent?

Answer: They are unit vectors. They are used to represent the horizontal and vertical components of a vector. They each have a magnitude of $1$.

4) What is component form?

5) When a unit vector is expressed as $\left \langle a,b \right \rangle$ which letter is the coefficient of the $i$ and which the $j$?

Answer: The first number always represents the coefficient of the $i$ and the second represents the $j$.

Algebraic

6) Given a vector with initial point $(5,2)$ and terminal point $(-1,-3)$, find an equivalent vector whose initial point is $(0,0)$. Write the vector in component form $\left \langle a,b \right \rangle$.

7) Given a vector with initial point $(-4,2)$ and terminal point $(3,-3)$, find an equivalent vector whose initial point is $(0,0)$. Write the vector in component form $\left \langle a,b \right \rangle$.

Answer: $\left \langle 7,-5 \right \rangle$

8) Given a vector with initial point $(7,-1)$ and terminal point $(-1,-7)$, find an equivalent vector whose initial point is $(0,0)$. Write the vector in component form $\left \langle a,b \right \rangle$.

For the exercises 9-15, determine whether the two vectors $u$ and $v$ are equal, where $u$ has an initial point $P_1$ and a terminal point $P_2$ and $v$ has an initial point $P_3$ and a terminal point $P_4$.

9) $P_1=(5,1), P_2=(3,-2), P_3=(-1,3), P4=(9,−4)$

Answer: not equal

10) $P_1=(2,-3), P_2=(5,1), P_3=(6,-1), P_4=(9,3)$

11) $P_1=(-1,-1), P_2=(-4,5), P_3=(-10,6), P_4=(-13,12)$

Answer: equal

12) $P_1=(3,7), P_2=(2,1), P_3=(1,2), P_4=(-1,-4)$

13) $P_1=(8,3), P_2=(6,5), P_3=(11,8), P4=(9,10)$

Answer: equal

14) Given initial point $P_1=(-3,1)$ and terminal point $P_2=(5,2)$, write the vector $v$ in terms of $i$ and $j$.

15) Given initial point $P_1=(6,0)$ and terminal point $P_2=(-1,-3)$, write the vector $v$ in terms of $i$ and $j$.

Answer: $7i-3j$

For the exercises 16-17, use the vectors $u = i+5j, v = -2i-3j, w = 4i-j$

16) Find $u+(v-w)$

17) Find $4v+2u$

Answer: $-6i-2j$

For the exercises 18-21, use the given vectors to compute $u + v, u - v, 2u - 3v$

18) $u=\left \langle 2,-3 \right \rangle, v=\left \langle 1,5 \right \rangle$

19) $u=\left \langle -3,4 \right \rangle, v=\left \langle -2,1 \right \rangle$

Answer: $u+v=\left \langle -5,5 \right \rangle,u-v=\left \langle -1,3 \right \rangle,2u-3v=\left \langle 0,5 \right \rangle$

20) Let $v = -4i + 3j$. Find a vector that is half the length and points in the same direction as $v$.

21) Let $v = 5i + 2j$. Find a vector that is twice the length and points in the opposite direction as $v$.

Answer: $-10i-4j$

For the exercises 22-27, find a unit vector in the same direction as the given vector.

22) $a = 3i + 4j$

23) $b = -2i + 5j$

Answer: $-\dfrac{2\sqrt{29}}{29}i+\dfrac{5\sqrt{29}}{29}j$

24) $c = 10i - j$

25) $d=-\dfrac{1}{3}i+\dfrac{5}{2}j$

Answer: $-\dfrac{2\sqrt{229}}{229}i+\dfrac{15\sqrt{229}}{229}j$

26) $u = 100i + 200j$

27) $u = -14i + 2j$

Answer: $-\dfrac{7\sqrt{2}}{10}i+\dfrac{\sqrt{2}}{10}j$

28) $\left \langle 0,4 \right \rangle$

29) $\left \langle 6,5 \right \rangle$

Answer: $\left | v \right |=7.810, \theta =39.806^{\circ}$

30) $\left \langle 2,-5 \right \rangle$

31) $\left \langle -4,-6 \right \rangle$

Answer: $\left | v \right |=7.211, \theta =236.310^{\circ}$

32) Given $u = 3i − 4j$ and $v = −2i + 3j$, calculate $u\cdot v$.

33) Given $u = −i − j$ and $v = i + 5j$, calculate $u\cdot v$.

Answer: $-6$

34) Given $u=\left \langle -2,4 \right \rangle$ and $v=\left \langle -3,1 \right \rangle$calculate $u\cdot v$.

35) Given $u=\left \langle -1,6 \right \rangle$ and $v=\left \langle 6,-1 \right \rangle$ calculate $u\cdot v$.

Answer: $-12$

Graphical

For the exercises 36-,38 given $v$, draw $v$, $3v$, and $\dfrac{1}{2}v$.

36) $\left \langle 2,-1 \right \rangle$

37) $\left \langle -1,4 \right \rangle$

Answer: $CNX_Precalc_Figure_08_08_253.jpg$

38) $\left \langle -3,-2 \right \rangle$

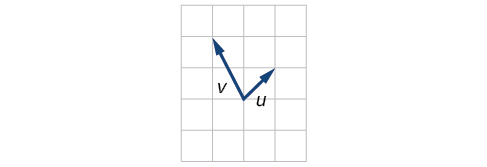
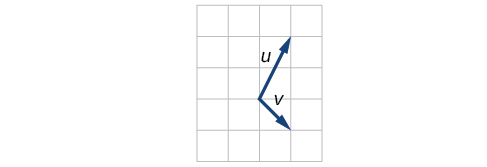
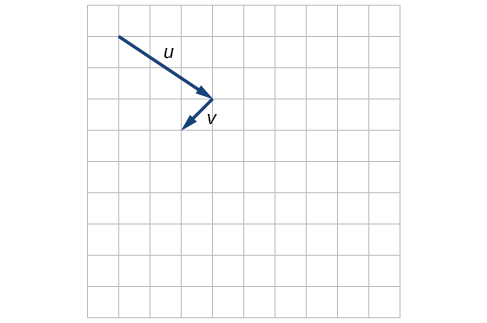
For the exercises 39-41, use the vectors shown to sketch $u + v$, $u − v$, and $2u$.

39)

$CNX_Precalc_Figure_08_08_204.jpg$

Answer: $CNX_Precalc_Figure_08_08_205.jpg$

40)

$CNX_Precalc_Figure_08_08_206.jpg$

41)

$CNX_Precalc_Figure_08_08_208.jpg$

Answer: $CNX_Precalc_Figure_08_08_209.jpg$

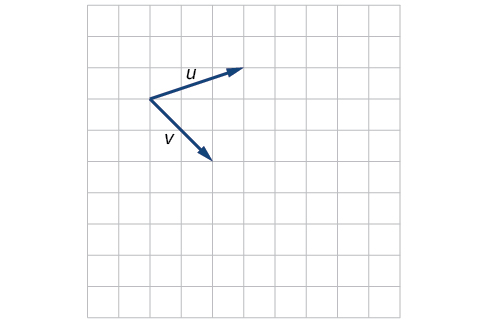
For the exercises 42-43, use the vectors shown to sketch $2u + v$.

42)

$CNX_Precalc_Figure_08_08_210.jpg$

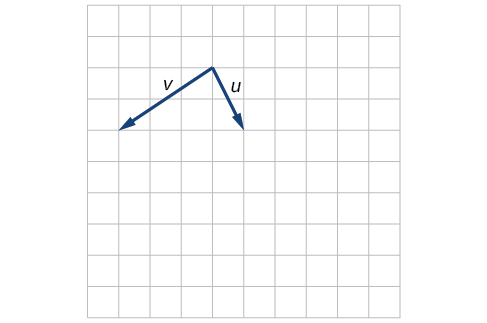
43)

$CNX_Precalc_Figure_08_08_212.jpg$

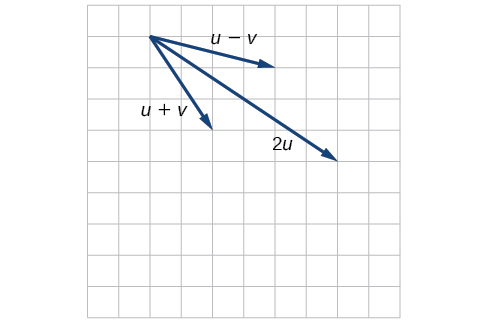
Answer: $CNX_Precalc_Figure_08_08_213.jpg$

For the exercises 44-45, use the vectors shown to sketch $u − 3v$.

44)

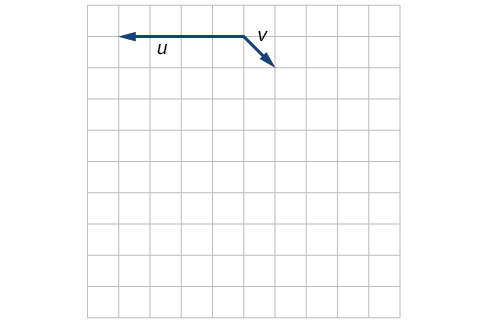
$CNX_Precalc_Figure_08_08_214.jpg$

45)

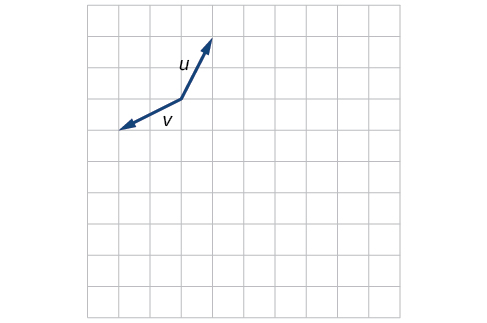
$CNX_Precalc_Figure_08_08_216.jpg$

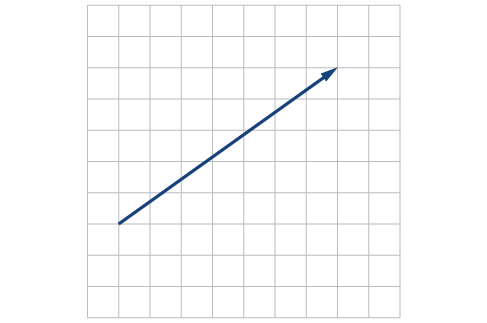
Answer: $CNX_Precalc_Figure_08_08_217.jpg$

For the exercises 46-47, write the vector shown in component form.

46)

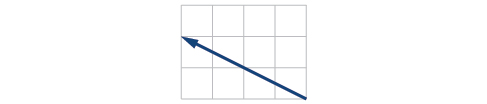
$CNX_Precalc_Figure_08_08_218.jpg$

47)

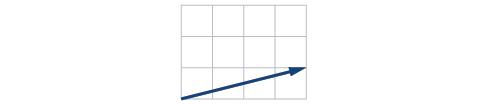
$CNX_Precalc_Figure_08_08_219.jpg$

Answer: $\left \langle 4,1 \right \rangle$

48) Given initial point $P_1=(2,1$ and terminal point $P_2=(-1,2)$ write the vector $v$ in terms of $i$ and $j$, then draw the vector on the graph.

49) Given initial point $P_1=(4,-1$ and terminal point $P_2=(-3,2)$, write the vector $v$ in terms of $i$ and $j$. Draw the points and the vector on the graph.

Answer

$v=-7i+3j$

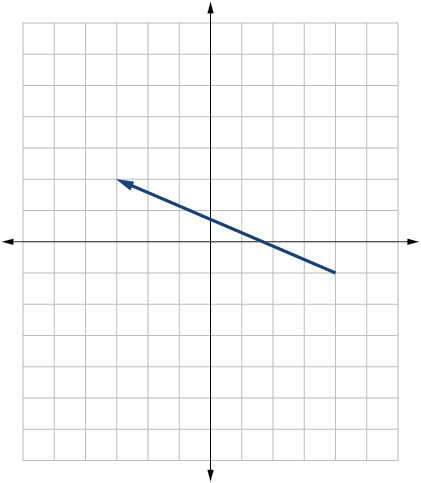
$CNX_Precalc_Figure_08_08_221.jpg$

50) Given initial point $P_1=(3,3$ and terminal point $P_2=(-3,3)$, write the vector $v$ in terms of $i$ and $j$. Draw the points and the vector on the graph.

Extensions

For the exercises 51-54, use the given magnitude and direction in standard position, write the vector in component form.

51) $\left | v \right |=6, \theta =45^{\circ}$

Answer: $3\sqrt{2}i+3\sqrt{2}j$

52) $\left | v \right |=8, \theta =220^{\circ}$

53) $\left | v \right |=2, \theta =300^{\circ}$

Answer: $i-\sqrt{3}j$

54) $\left | v \right |=5, \theta =135^{\circ}$

55) A $60$-pound box is resting on a ramp that is inclined $12^{\circ}$. Rounding to the nearest tenth,

Find the magnitude of the normal (perpendicular) component of the force.
Find the magnitude of the component of the force that is parallel to the ramp.

Answer

$58.7$
$12.5$

56) A $25$-pound box is resting on a ramp that is inclined $8^{\circ}$. Rounding to the nearest tenth,

Find the magnitude of the normal (perpendicular) component of the force.
Find the magnitude of the component of the force that is parallel to the ramp.

57) Find the magnitude of the horizontal and vertical components of a vector with magnitude $8$ pounds pointed in a direction of $27^{\circ}$ above the horizontal. Round to the nearest hundredth.

Answer: $x=7.13$ pounds, $y=3.63$ pounds

58) Find the magnitude of the horizontal and vertical components of the vector with magnitude $4$ pounds pointed in a direction of $127^{\circ}$ above the horizontal. Round to the nearest hundredth.

59) Find the magnitude of the horizontal and vertical components of a vector with magnitude $5$ pounds pointed in a direction of $55^{\circ}$ above the horizontal. Round to the nearest hundredth.

Answer: $x=2.87$ pounds, $y=4.10$ pounds

60) Find the magnitude of the horizontal and vertical components of the vector with magnitude $1$ pound pointed in a direction of $8^{\circ}$ above the horizontal. Round to the nearest hundredth.

Real-World Applications

61) A woman leaves home and walks $3$ miles west, then $2$ miles southwest. How far from home is she, and in what direction must she walk to head directly home?

Answer: $4.635$ miles, $17.764^{\circ}$ N of E

62) A boat leaves the marina and sails $6$ miles north, then $2$ miles northeast. How far from the marina is the boat, and in what direction must it sail to head directly back to the marina?

63) A man starts walking from home and walks $4$ miles east, $2$ miles southeast, $5$ miles south, $4$ miles southwest, and $2$ miles east. How far has he walked? If he walked straight home, how far would he have to walk?

Answer: $17$ miles, $10.318$ miles

64) A woman starts walking from home and walks $4$ miles east, $7$ miles southeast, $6$ miles south, $5$ miles southwest, and $3$ miles east. How far has she walked? If she walked straight home, how far would she have to walk?

65) A man starts walking from home and walks $3$ miles at $20^{\circ}$ north of west, then $5$ miles at $10^{\circ}$ west of south, then $4$ miles at $15^{\circ}$ north of east. If he walked straight home, how far would he have to the walk, and in what direction?

Answer: Distance: $2.868$, Direction: $86.474^{\circ}$ North of West, or $3.526^{\circ}$ West of North

66) A woman starts walking from home and walks $6$ miles at $40^{\circ}$ north of east, then $2$ miles at $15^{\circ}$ east of south, then $5$ miles at $30^{\circ}$ south of west. If she walked straight home, how far would she have to walk, and in what direction?

67) An airplane is heading north at an airspeed of $600$ km/hr, but there is a wind blowing from the southwest at $80$ km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?

Answer: $4.924^{\circ}$, 659 km/hr

68) An airplane is heading north at an airspeed of $500$ km/hr, but there is a wind blowing from the northwest at $50$ km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?

69) An airplane needs to head due north, but there is a wind blowing from the southwest at $60$ km/hr. The plane flies with an airspeed of $550$ km/hr. To end up flying due north, how many degrees west of north will the pilot need to fly the plane?

Answer: $4.424^{\circ}$

70) An airplane needs to head due north, but there is a wind blowing from the northwest at $80$ km/hr. The plane flies with an airspeed of $500$ km/hr. To end up flying due north, how many degrees west of north will the pilot need to fly the plane?

71) As part of a video game, the point $(5,7)$ is rotated counterclockwise about the origin through an angle of $35^{\circ}$. Find the new coordinates of this point.

Answer: $(0.081,8.602)$

72) As part of a video game, the point $(7,3)$ is rotated counterclockwise about the origin through an angle of $40^{\circ}$. Find the new coordinates of this point.

73) Two children are throwing a ball back and forth straight across the back seat of a car. The ball is being thrown $10$ mph relative to the car, and the car is traveling $25$ mph down the road. If one child doesn't catch the ball, and it flies out the window, in what direction does the ball fly (ignoring wind resistance)?

Answer: $21.801^{\circ}$, relative to the car’s forward direction

74) Two children are throwing a ball back and forth straight across the back seat of a car. The ball is being thrown $8$ mph relative to the car, and the car is traveling $45$ mph down the road. If one child doesn't catch the ball, and it flies out the window, in what direction does the ball fly (ignoring wind resistance)?

75) A $50$-pound object rests on a ramp that is inclined $19^{\circ}$. Find the magnitude of the components of the force parallel to and perpendicular to (normal) the ramp to the nearest tenth of a pound.

Answer: parallel: $16.28$, perpendicular: $47.28$ pounds

76) Suppose a body has a force of $10$ pounds acting on it to the right, $25$ pounds acting on it upward, and $5$ pounds acting on it $45^{\circ}$ from the horizontal. What single force is the resultant force acting on the body?

77) Suppose a body has a force of $10$ pounds acting on it to the right, $25$ pounds acting on it ─$135^{\circ}$ from the horizontal, and $5$ pounds acting on it directed $150^{\circ}$ from the horizontal. What single force is the resultant force acting on the body?

Answer: $19.35$ pounds, $231.54^{\circ}$ from the horizontal

78) The condition of equilibrium is when the sum of the forces acting on a body is the zero vector. Suppose a body has a force of $2$ pounds acting on it to the right, $5$ pounds acting on it upward, and $3$ pounds acting on it $45^{\circ}$ from the horizontal. What single force is needed to produce a state of equilibrium on the body?

79) Suppose a body has a force of $3$ pounds acting on it to the left, $4$ pounds acting on it upward, and $2$ pounds acting on it $30^{\circ}$ from the horizontal. What single force is needed to produce a state of equilibrium on the body? Draw the vector.

Answer: $5.1583$ pounds, $75.8^{\circ}$ from the horizontal

More Practice w/Vectors

For the exercises 1-2, determine whether the two vectors, $u$ and $v$, are equal, where $u$ has an initial point $P_1$ and a terminal point $P_2$, and $v$ has an initial point $P_3$ and a terminal point $P_4$.

1) $P_1=(-1,4), P_2=(3,1), P_3=(5,5), P_4=(9,2)$

2) $P_1=(6,11), P_2=(-2,8), P_3=(0,-1), P_4=(-8,2)$

Answer: not equal

For the exercises 3-4, use the vectors $u=2i-j,v=4i-3j$, and $w=-2i+5j$ to evaluate the expression.

3) $u-v$

4) $2v-u+w$

Answer: $4i$

For the exercises 5-6, find a unit vector in the same direction as the given vector.

5) $a=8i-6j$

6) $b=-3i-j$

Answer: $-\dfrac{3\sqrt{10}}{10}i-\dfrac{\sqrt{10}}{10}j$

For the exercises 7-11, calculate $u\cdot v$.

7) $u=-2i+j$ and $v=3i+7j$

8) $u=i+4j$ and $v=4i+3j$

Answer: $16$

9) Given $v=\left \langle -3,4 \right \rangle$ draw $v$, $2v$, and $\dfrac{1}{2}v$.

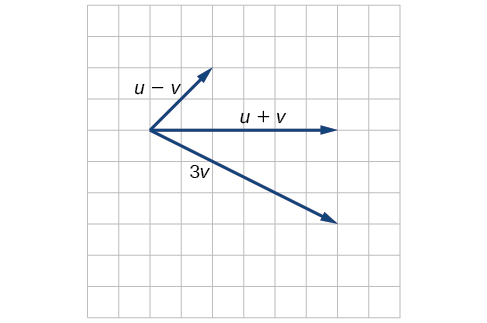
10) Given the vectors shown in the Figure below, sketch $u + v$, $u − v$ and $3v$.

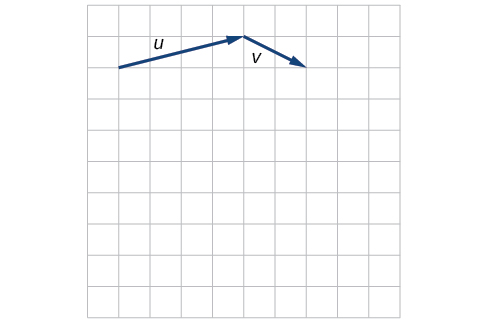
$Ex 8R 8.8.10.png$

Answer: $Ex 8R 8.8.10 sol.png$

11) Given initial point $P_1=(3,2)$ and terminal point $P_2=(-5,-1)$write the vector $v$ in terms of $i$ and $j$. Draw the points and the vector on the graph.

Search

Text Color

Text Size

Margin Size

Font Type