3.5: Introduction to Percents- Percents as Fractions and Decimals
- Last updated
- Jan 8, 2020
- Save as PDF
- Page ID
- 30992
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the square shown in Figure 3.5.1, a large square has been partitioned into ten rows of ten little squares in each row. In Figure 7.1, we’ve shaded 20 of 100 possible little squares, or 20% of the total number of little squares.
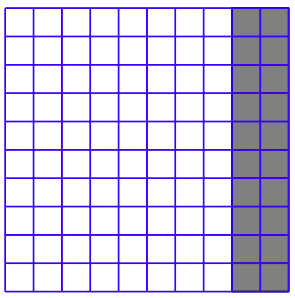
The Meaning of Percent
Percent means “parts per hundred.”
In Figure 7.1, 80 out of a possible 100 squares are left unshaded. Thus, 80% of the little squares are unshaded. If instead we shaded 35 out of the 100 squares, then 35% of the little squares would be shaded. If we shaded all of the little squares, then 100% of the little squares would be shaded (100 out of 100).
So, when you hear the word “percent,” think “parts per hundred.”
Changing a Percent to a Fraction
Based on the discussion above, it is fairly straightforward to change a percent to a fraction.
Percent to Fraction
To change a percent to a fraction, drop the percent sign and put the number over 100.
Example 1
Change 24% to a fraction.
Solution
Drop the percent symbol and put 24 over 100.
24%=24100 Percent: Parts per hundred.=625 Reduce.
Hence, 24% = 6/25.
Exercise
Change 36% to a fraction reduced to lowest terms.
- Answer
-
9/25
Example 2
Change 1427% to a fraction.
Solution
Drop the percent symbol and put 1427 over 100.
1427%=1427100 Percent: Parts per hundred.=1007100 Mixed to improper fraction.=1007⋅1100 Invert and multiply.=1007⋅1100 Cancel.=17
Hence, 1427%=1/7.
Exercise
Change 1119% to a fraction reduced to lowest terms.
- Answer
-
1/9
Example 3
Change 28.4% to a fraction.
Solution
Drop the percent symbol and put 28.4 over 100.
28.4%=28.4100 Percent: Parts per hundred.=28.4⋅10100⋅10 Multiply numerator and denominator by 10.=2841000 Multiplying by 10 moves decimal point one place right.=71⋅4250⋅4 Factor.=71250 Cancel common factor.
Exercise
Change 87.5% to a fraction reduced to lowest terms.
- Answer
-
7/8
Changing a Percent to a Decimal
To change a percent to a decimal, we need only remember that percent means “parts per hundred.”
Example 4
Change 23.25% to a decimal.
Solution
Drop the percent symbol and put 23.25 over 100.
23.25%=23.25100 Percent: Parts per hundred.=0.2325 Dividing by 100 moves decimal point 2 places left.
Therefore, 23.25% = 0.2325.
Exercise
Change 2.4% to a decimal.
- Answer
-
0.024
This last example motivates the following simple rule.
Changing a Percent to a Decimal
To change a percent to a decimal, drop the percent symbol and move the decimal point two places to the left.
Example 5
Change 512% to a decimal.
Solution
Note that 1/2=0.5, then move the decimal 2 places to the left.
512%=5.5% 1/2=0.5.=0.055 Drop % symbol. Move decimal point 2 places left.=0.055
Thus, 512%=0.055.
Exercise 3.5.1
Change 634% to a decimal.
- Answer
-
0.0675
Changing a Decimal to a Percent
Changing a decimal to a percent is the exact opposite of changing a percent to a decimal. In the latter case, we drop the percent symbol and move the decimal point 2 places to the left. The following rule does just the opposite.
Changing a Decimal to a Percent
To change a decimal to a percent, move the decimal point two places to the right and add a percent symbol.
Example 6
Change 0.0725 to a percent.
Solution
Move the decimal point two places to the right and add a percent symbol.
0.0725=007.25%=7.25%
Exercise
Change to 0.0375 to a percent.
- Answer
-
3.75%
Example 7
Change 1.025 to a percent.
Solution
Move the decimal point two places to the right and add a percent symbol.
1.025=102.5%=102.5%
Exercise
Change 0.525 to a percent.
- Answer
-
52.5%
Changing a Fraction to a Percent
One way to proceed is to first change the fraction to a decimal, then change the resulting decimal to a percent.
Fractions to Percents: Technique #1
To change a fraction to a percent, follow these steps:
- Divide numerator by the denominator to change the fraction to a decimal.
- Move the decimal point in the result two places to the right and append a percent symbol.
Example 8
Use Technique #1 to change 5/8 to a percent.
Solution
Change 5/8 to a decimal, then change the decimal to a percent.
To change 5/8 to a decimal, divide 5 by 8. Since the denominator is a product of twos, the decimal should terminate.
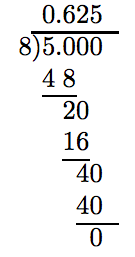
To change 0.625 to a percent, move the decimal point 2 places to the right and append a percent symbol.
0.625 = 0 62.5% = 62.5%
Exercise
Change 5/16 to a percent.
- Answer
-
31.35%
A second technique is to create an equivalent fraction with a denominator of 100.
Fractions to Percents: Technique #2
To change a fraction to a percent, create an equivalent fraction with a denominator of 100.
Example 9
Use Technique #2 to change 5/8 to a percent.
Solution
Create an equivalent fraction for 5/8 with a denominator of 100.
58=x100
Solve this proportion for x.
8x=500 Cross multiply.8x8=5008 Divide both sides by 8.x=1252 Reduce: Divide numerator and denominator by 4.x=62.5 Divide.
Thus,
58=62.5100=62.5%.
Alternate Ending
We could also change 125/2 to a mixed fraction; i.e., 125/2 = 62 1 2 . Then,
58=6212100=6212%.
Same answer.
Exercise
Change 4/9 to a percent.
- Answer
-
4449%
Sometimes we will be content with an approximation.
Example 10
Change 4/13 to a percent. Round your answer to the nearest tenth of a percent.
Solution
We will use Technique #1.
To change 4/13 to a decimal, divide 4 by 13. Since the denominator has factors other than 2’s and 5’s, the decimal will repeat. However, we intend to round to the nearest tenth of a percent, so we will carry the division to four decimal places only. (Four places are necessary because we will be moving the decimal point two places to the right.)
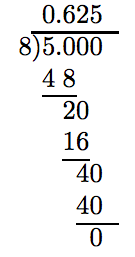
To change the decimal to a percent, move the decimal point two places to the right.
0.3076 ≈ 0 30.76% ≈ 30.76%
To round to the nearest tenth of a percent, identify the rounding and test digits.
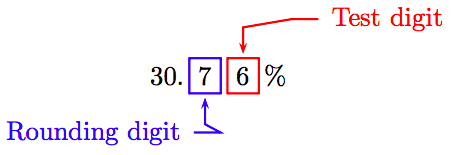
Because the test digit is greater than or equal to 5, add 1 to the rounding digit and truncate. Thus,
0.03076 ≈ 30.8%.
Exercise
Change 4/17 to a percent. Round your answer to the nearest tenth of a percent.
- Answer
-
23.5%
Exercises
In Exercises 1-18, convert the given percent to a fraction, and simplify the result.
1. 4710%
2. 714%
3. 729%
4. 4910%
5. 11.76%
6. 15.2%
7. 13.99%
8. 18.66%
9. 412%
10. 858%
11. 192%
12. 5%
13. 86%
14. 177%
15. 130%
16. 80%
17. 4.07%
18. 6.5%
In Exercises 19-34, convert the given percent to a decimal.
19. 124%
20. 4%
21. 0.6379%
22. 0.21%
23. 28%
24. 5.4%
25. 0.83%
26. 0.3344%
27. 8%
28. 3%
29. 59.84%
30. 0.17%
31. 155%
32. 7%
33. 36.5%
34. 39.7%
In Exercises 35-50, convert the given decimal to a percent.
35. 8.888
36. 5.1
37. 0.85
38. 0.08
39. 1.681
40. 3.372
41. 0.14
42. 4.89
43. 8.7
44. 8.78
45. 0.38
46. 1.67
47. 0.02
48. 0.07
49. 0.044
50. 0.29
In Exercises 51-68, convert the given fraction to a percent.
51. 12
52. 298
53. 52
54. 45
55. 85
56. 720
57. 145
58. 32
59. 92
60. \(\frac{18}{25}|)
61. 94
62. 78
63. 75
64. 425
65. 65
66. 238
67. 125
68. 132
69. Convert 24/29 to a percent, and round your answer to the nearest hundredth of a percent.
70. Convert 5/3 to a percent, and round your answer to the nearest hundredth of a percent.
71. Convert 15/7 to a percent, and round your answer to the nearest tenth of a percent.
72. Convert 10/7 to a percent, and round your answer to the nearest tenth of a percent.
73. Convert 7/24 to a percent, and round your answer to the nearest hundredth of a percent.
74. Convert 5/6 to a percent, and round your answer to the nearest hundredth of a percent.
75. Convert 8/3 to a percent, and round your answer to the nearest tenth of a percent.
76. Convert 22/21 to a percent, and round your answer to the nearest tenth of a percent.
77. Convert 9/23 to a percent, and round your answer to the nearest tenth of a percent.
78. Convert 11/9 to a percent, and round your answer to the nearest tenth of a percent.
79. Convert 17/27 to a percent, and round your answer to the nearest hundredth of a percent.
80. Convert 22/27 to a percent, and round your answer to the nearest hundredth of a percent.
81. Crime rates. Preliminary crime rates for the first six months of 2009 compared to the same period in 2008 are shown below. Associated Press-Times-Standard 12/22/09 Despite recession, the national crime rates keep falling.
Murder −10.0%Forcible rape −3.3%Robbery −6.5%Aggravated assault −3.2%Burglary −2.5%Larceny-theft −5.3%Motor vehicle theft −18.75%Arson −8.2%
Source: Federal Bureau of Investigation
i) What do the negative signs indicate?
ii) Which type of crime decreased the most?
iii) Which type of crime decreased the least?
82. Major Hurricanes. 5 of the 8 hurricanes in 2008 were categorized as major. Write the fractional number of major hurricanes in 2008 as a percent. NOAA Associated Press 5/22/09
83. Chance of flood. These excerpts are from the story Corps: Dam work lessens Seattle-area flood chance published in the Times-Standard on Nov. 6, 2009. Write all four of the odds of flooding as a percent chance. Round to the nearest tenth of a percent if necessary.
i) Col. Anthony Wright, from the U.S. Army Corps of Engineers, speaking of the repairs to the Green River Dam, reported there was now a 1-in-25 chance that a storm would force the corps to release enough water from the dam’s reservoir to cause a flood downstream in the Green River Valley.
ii) The odds of widespread flooding in the valley improve to 1-in-32 when all the sandbagging and flood-protection efforts are factored in.
iii) Previously, the Corps of Engineers said the chance of widespread flooding was 1-in-4.
iv) When the dam operates at capacity, there is a 1-in-140 chance of flooding.
Answers
1. 471000
3. 13180
5. 1471250
7. 139910000
9. 9200
11. 4825
13. 4350
15. 1310
17. 40710000
19. 1.24
21. 0.006379
23. 0.28
25. 0.0083
27. 0.08
29. 0.5984
31. 1.55
33. 0.365
35. 888.8%
37. 85%
39. 168.1%
41. 14%
43. 870%
45. 38%
47. 2%
49. 4.4%
51. 50%
53. 250%
55. 160%
57. 280%
59. 450%
61. 225%
63. 140%
65. 120%
67. 240%
69. 82.76%
71. 214.3%
73. 29.17%
75. 266.7%
77. 39.1%
79. 62.96%
81.
i) The negative signs indicate the crime rate has decreased from previous measures.
ii) Motor vehicle theft decreased the most with an 18.75% decrease.
iii) Burglary decreased the least with a 2.5% decrease.
83.
i) 4% chance of flood
ii) 3.1% chance of flood
iii) 25% chance of flood
iv) 0.7% chance of flood


