1.2: Percent
- Page ID
- 93850
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Understand the definition and the meaning of percent notation.
- Convert between percent, fraction, and decimal notations.
- Use and understand percent notation in context
When one hears the word “percent,” other words come immediately to mind, words such as “century,” “cents,” or “centimeters.” A century equals 100 years. There are one hundred cents in a dollar and there are 100 centimeters in a meter. Thus, it should come as no surprise that percent means “parts per hundred.”
In the world we live in we are constantly bombarded with phrases that contain the word “percent.” The sales tax in California is 8.25%. An employee is asking his boss for a 5% raise. A union has seen a 6.25% increase in union dues. The population of a town is increasing at a rate of 2.25% per year.
In this section, we introduce the concept of percent, first addressing how to facilitate writing percents in fraction or decimal form and also performing the reverse operations, changing fractions and decimals to percents. Eventually, we apply this ability to solving common applications from the real world that use percents. We’ll tackle applications of commission and sales tax, discount and marked price, percent increase or decrease, and simple and compound interest.
Let’s begin the journey! In the square shown in Figure \(\PageIndex{1}\), a large square has been partitioned into ten rows of ten little squares in each row. In Figure 7.1, we’ve shaded 20 of 100 possible little squares, or 20% of the total number of little squares.
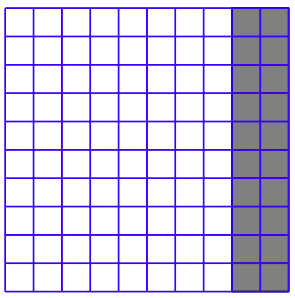
Percent means “parts per hundred.”
In Figure (\PageIndex{1}\), 80 out of a possible 100 squares are left unshaded. Thus, 80% of the little squares are unshaded. If instead we shaded 35 out of the 100 squares, then 35% of the little squares would be shaded. If we shaded all of the little squares, then 100% of the little squares would be shaded (100 out of 100).
So, when you hear the word “percent,” think “parts per hundred.”
Changing a Percent to a Fraction
Based on the discussion above, it is fairly straightforward to change a percent to a fraction.
To change a percent to a fraction, drop the percent sign and put the number over 100.
Change 24% to a fraction.
Solution
Drop the percent symbol and put 24 over 100.
\[ \begin{aligned} 24 \% = \frac{24}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{6}{25} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]
Hence, 24% = 6/25.
Change 36% to a fraction reduced to lowest terms.
- Answer
-
9/25
Change 28.4% to a fraction.
Solution
Drop the percent symbol and put 28.4 over 100.
\[ \begin{aligned} 28.4 \% = \frac{28.4}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{28.4 \cdot \textcolor{red}{10}}{100 \cdot \textcolor{red}{10}} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 10.}} \\ = \frac{284}{1000} ~ & \textcolor{red}{ \text{ Multiplying by 10 moves decimal point one place right.}} \\ = \frac{71 \cdot 4}{250 \cdot 4} ~ & \textcolor{red}{ \text{ Factor.}} \\ = \frac{71}{250} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \end{aligned}\nonumber \]
Change 87.5% to a fraction reduced to lowest terms.
- Answer
-
7/8
Exercise \(\PageIndex{2}\)
Changing a Percent to a Decimal
To change a percent to a decimal, we need only remember that percent means “parts per hundred.”
Change 23.25% to a decimal.
Solution
Drop the percent symbol and put 23.25 over 100.
\[ \begin{aligned} 23.25 \% = \frac{23.25}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = 0.2325 ~ & \textcolor{red}{ \text{ Dividing by 100 moves decimal point 2 places left.}} \end{aligned}\nonumber \]
Therefore, 23.25% = 0.2325.
Change 2.4% to a decimal.
- Answer
-
0.024
This last example motivates the following simple rule.
To change a percent to a decimal, drop the percent symbol and move the decimal point two places to the left.
Changing a Decimal to a Percent
Changing a decimal to a percent is the exact opposite of changing a percent to a decimal. In the latter case, we drop the percent symbol and move the decimal point 2 places to the left. The following rule does just the opposite.
To change a decimal to a percent, move the decimal point two places to the right and add a percent symbol.
Change 0.0725 to a percent.
Solution
Move the decimal point two places to the right and add a percent symbol.
\[ \begin{aligned} 0.0725 = 007.25 \% \\ = 7.25 \% \end{aligned}\nonumber \]
Change to 0.0375 to a percent.
- Answer
-
3.75%
Interactive Exercise \(\PageIndex{4}\)
Change 1.025 to a percent.
Solution
Move the decimal point two places to the right and add a percent symbol.
\[ \begin{aligned} 1.025 = 102.5 \% \\ = 102.5 \% \end{aligned}\nonumber \]
Change 2.525 to a percent.
- Answer
-
252.5%
Interactive Exercise \(\PageIndex{5}\)
Changing a Fraction to a Percent
One way to proceed is to first change the fraction to a decimal, then change the resulting decimal to a percent.
To change a fraction to a percent, follow these steps:
- Divide the numerator by the denominator to change the fraction to a decimal.
- Move the decimal point in the result two places to the right and append a percent symbol.
Use Technique #1 to change 5/8 to a percent.
Solution
Change 5/8 to a decimal, then change the decimal to a percent.
To change 5/8 to a decimal, divide 5 by 8. Since the denominator is a product of twos, the decimal should terminate.
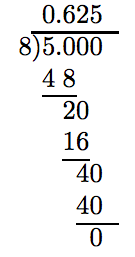
To change 0.625 to a percent, move the decimal point 2 places to the right and append a percent symbol.
0.625 = 0 62.5% = 62.5%
Change 5/16 to a percent.
- Answer
-
31.35%
Interactive Exercise \(\PageIndex{6}\)
A second technique is to create an equivalent fraction with a denominator of 100.
To change a fraction to a percent, create an equivalent fraction with a denominator of 100. This technique should only be used when the denominator of the fraction is a divisor of 100.
Use Technique #2 to change 3/5 to a percent.
Solution
Note that the denominator 5 is a divisor of 100, that is 100=5*20. To create an equivalent fraction for 3/5 with a denominator of 100 multiple both, the numerator and denominator, by 20:
\[ \frac{3}{5} = \frac{3\cdot20}{5\cdot20} = \frac{60}{100} \]
Thus,
\[ \frac{3}{5} = 60 \%.\nonumber \]
Change 4/25 to a percent.
- Answer
-
\(16\%\)
Interactive Exercise \(\PageIndex{7}\)
Sometimes we will be content with an approximation.
Change 4/13 to a percent. Round your answer to the nearest tenth of a percent.
Solution
We will use Technique #1.
To change 4/13 to a decimal, divide 4 by 13. Since the denominator has factors other than 2’s and 5’s, the decimal will repeat. However, we intend to round to the nearest tenth of a percent, so we will carry the division to four decimal places only. (Four places are necessary because we will be moving the decimal point two places to the right.)
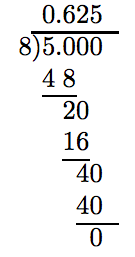
To change the decimal to a percent, move the decimal point two places to the right.
0.3076 ≈ 0 30.76% ≈ 30.76%
To round to the nearest tenth of a percent, identify the rounding and test digits.
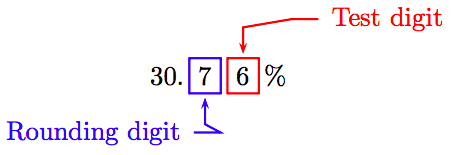
Because the test digit is greater than or equal to 5, add 1 to the rounding digit and truncate. Thus,
0.03076 ≈ 30.8%.
Change 4/17 to a percent. Round your answer to the nearest tenth of a percent.
- Answer
-
23.5%
Interactive Exercise \(\PageIndex{8}\)
Using Percent in Context
5 of the 8 hurricanes in 2008 were categorized as major. Write the fractional number of major hurricanes in 2008 as a percent. NOAA Associated Press 5/22/09
Solution
\(\dfrac{5}{8}=0.625=62.5\%\)
The 2021 hurricane season produced seven hurricanes—Elsa, Grace, Henri, Ida, Larry, Nicholas and Sam. Four hurricanes—Grace, Ida, Larry and Sam—reached major hurricane status (Category 3 and above). Ida and Sam reached Category 4 status. (Source: Facts + Statistics: Hurricanes | III) Write the fractional number of major hurricanes in 2021 as a percent.
- Answer
-
\(\dfrac{4}{7}=0.5714=57.14\%\)
Interactive Exercise \(\PageIndex{9}\)


