1.3: Algebra Essentials
- Page ID
- 93844
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Evaluate and simplify algebraic expressions.
- Solve an equation
- Use a formula
So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as \(x +5\), \(\dfrac{4}{3}\pi r^3\), or \(\sqrt{2m^3 n^2}\). In the expression \(x +5\), \(5\) is called a constant because it does not vary and \(x\) is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.
We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.
\[\begin{align*} (-3)^5 &=(-3)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow x^5=x\times x\times x\times x\times x\\ (2\times7)^3&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{align*}\]
In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.
Evaluating Algebraic Expressions
Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.
List the constants and variables for each algebraic expression.
- \(x + 5\)
- \(\dfrac{4}{3}\pi r^3\)
- \(\sqrt{2m^3 n^2}\)
Solution
| Constants | Variables | |
|---|---|---|
| a. \(x + 5\) | \(5\) | \(x\) |
| b. \(\dfrac{4}{3}\pi r^3\) | \(\dfrac{4}{3}\), \(\pi\) | \(r\) |
| c. \(\sqrt{2m^3 n^2}\) | \(2\) | \(m\),\(n\) |
List the constants and variables for each algebraic expression.
- \(2\pi r(r+h)\)
- \(2(L + W)\)
- \(4y^3+y\)
- Answer
-
Constants Variables a. \(2\pi r(r+h)\) \(2\),\(\pi\) \(r\),\(h\) b. \(2(L + W)\) \(2\) \(L\), \(W\) c. \(4y^3+y\) \(4\) \(y\)
- \(x=0\)
- \(x=1\)
- \(x=12\)
- \(x=−4\)
Solution
- Substitute \(0\) for \(x\). \[\begin{align*} 2x-7 &= 2(0)-7 \\ &= 0-7\\ &= -7\\ \end{align*}\]
- Substitute \(1\) for \(x\). \[\begin{align*} 2x-7 &= 2(1)-7 \\ &= 2-7\\ &= -5\\ \end{align*}\]
- Substitute \(\dfrac{1}{2}\) for \(x\). \[\begin{align*} 2x-7 &= 2\left (\dfrac{1}{2} \right )-7 \\ &= 1-7\\ &= -6\\ \end{align*}\]
- Substitute \(-4\) for \(x\). \[\begin{align*} 2x-7 &= 2(-4)-7 \\ &= -8-7\\ &= -15\\ \end{align*}\]
Evaluate the expression \(11−3y\) for each value for \(y\).
- \(y=2\)
- \(y=0\)
- \(y=\dfrac{2}{3}\)
- \(y=−5\)
- Answer
-
- \(5\)
- \(11\)
- \(9\)
- \(26\)
Interactive Exercise \(\PageIndex{2}\)
Evaluate each expression for the given values.
- \(x+5\) for \(x=-5\)
- \(\dfrac{t}{2t-1}\) for \(t=10\)
- \(\dfrac{4}{3}\pi r^3\) for \(r=5\)
- \(a+ab+b\) for \(a=11\), \(b=-8\)
- \(\sqrt{2m^3+n^2}\) for \(m=2\), \(n=3\)
Solution
- Substitute
\(-5\) for \(x\). \[\begin{align*} x+5 &= (-5)+5 \\ &= 0\\ \end{align*}\] - Substitute \(10\) for \(t\). \[\begin{align*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-1} \\ &= \dfrac{10}{20-1}\\ &= \dfrac{10}{19}\\ \end{align*}\]
- Substitute \(5\) for \(r\)
. \[\begin{align*} \dfrac{4}{3} \pi r^3 &= \dfrac{4}{3}\pi (5)^3 \\ &= \dfrac{4}{3}\pi (125)\\ &= \dfrac{500}{3}\pi\\ \end{align*}\] - Substitute \(11\) for \(a\) and \(-8\) for \(b\)
. \[\begin{align*} a+ab+b &= (11)+(11)(-8)+(-8) \\ &= 11-88-8 \\ &= -85\\ \end{align*}\] - Substitute \(2\) for \(m\) and \(3\) for \(n\). \[\begin{align*} \sqrt{2m^3+n^2} &= \sqrt{2(2)^3+(3)^2} \\ &= \sqrt{2(8)+(9)} \\ &= \sqrt{25} \\ &= 5 \end{align*}\]
Interactive Exercise \(\PageIndex{3}\)
Evaluating Algebraic Expressions with Technology
Luckily, when it comes to evaluating expressions, we can trust technology with performing this task. Instead of plugging in the values and computing by hand, let's discuss how technology can be used.
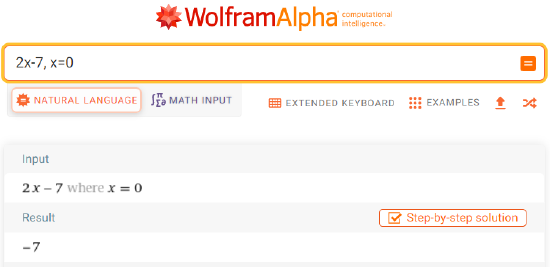
In Desmos Scientific Calculator, enter the expression then press Enter and enter \(x=\) followed by the value at which the expression is being evaluated. In case there are multiple variables involved, repeat the previous step for every additional variable. Once the values for all involved variables are entered the  notification will be replaced with the value of the expression. For example, evaluating \(2x-7\) at \(x=0\) from part (a) of Example \(\PageIndex{2}\) is shown below:
notification will be replaced with the value of the expression. For example, evaluating \(2x-7\) at \(x=0\) from part (a) of Example \(\PageIndex{2}\) is shown below:
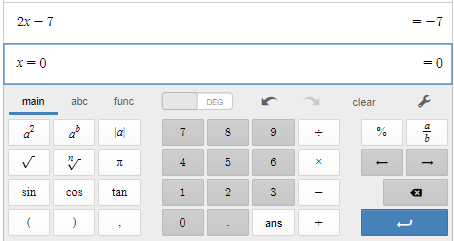
In WolframAlpha, enter the expression followed by the value at which the expression is being evaluated. In case there are multiple variables involved, repeat the previous step for every additional variable. Once the values for all involved variables are entered press Enter and the value of the expression will appear among the results. For example, evaluating \(2x-7\) at \(x=0\) from part (a) of Example \(\PageIndex{2}\) is shown below:
Evaluate each expression for the given values.
- \(\dfrac{y+3}{y-3}\) for \(y=5\)
- \(7-2t\) for \(t=-2\)
- \(\dfrac{1}{3}\pi r^2\) for \(r=11\)
- \((p^2 q)^3\) for \(p=-2\), \(q=3\)
- \(4(m-n)-5(n-m)\) for \(m=\dfrac{2}{3}\) \(n=\dfrac{1}{3}\)
- Answer
-
- \(4\)
- \(11\)
- \(\dfrac{121}{3}\pi\)
- \(1728\)
- \(3\)
Solving Equations
An equation is an expression that is equal to another expression. Unlike expressions, equations have an equal sign.
Examples of equations:
a) \(x-4=6\)
b) \(5 x-6=4 x+2\)
c) \(6 x-30=0\)
d) \(x^{2}+3 x-4=0\)
e) \(3 x^{2}-2 x=-1\)
f) \(x^{3}+x^{2}+x+1=0\)
g) \(2 x-5>3\) is not an equation but rather an inequality
A solution of an equation is any value of the variable that satisfies the equality, that is, it makes the Left-Hand Side (LHS) and the Right-Hand Side (RHS) of the equation the same value.
Solutions of equations:
a) A solution for \(x-4=6\) is \(x=10\) because the LHS evaluated at \(x=10\) is \(10-4=6\) which is equal to the \(\mathrm{RHS}\).
b) A solution for \(5 x-6=4 x+2\) is \(x=8\) because the LHS evaluated at \(x=8\) is \(5(8)-6=40-6=34\) and the RHS evaluated at \(x=8\) is \(4 x+2=4(8)+2=32+2=34,\) and they are equal!
So, given a value of \(x\), we can check if it is a solution or not by evaluating simultaneously the LHS and RHS of an equation. If they are equal, then the value is a solution. If they are not equal, then the value is not a solution.
a) Is \(x=2\) a solution of the equation
\[-4 x+8+x=5-2 x+1\nonumber\] ?
The LHS evaluated at \(x=2\) is \(-4(2)+8+2=-8+8+2=2\).
The RHS evaluated at \(x=2\) is \(5-2(2)+1=5-4+1=5+(-4)+1=1+1=2\).
Since they are equal, then we say that \(x=2\) is a solution for the given equation.
b) Is \(x=-1\) a solution of the equation
\[x^{2}+4 x=-3 x+8\nonumber\] ?
The LHS evaluated at \(x=-1\) is \((-1)^{2}+4(-1)=1+(-4)=-3\).
The RHS evaluated at \(x=-1\) is \(-3(-1)+8=3+8=11\).
Since \(-3 \neq 11\), then we say that \(x=-1\) is not a solution for the given equation.
c) Is \(x=-2\) a solution to
\[x^{2}-2 x+1=3 x^{2}+2 x+1\nonumber\] ?
The LHS evaluated at \(x=-2\) is \((-2)^{2}-2(-2)+1=4+4+1=9\).
The RHS evaluated at \(x=-2\) is \(3(-2)^{2}+2(-2)+1=3 \cdot 4-4+1=12-4+1=9 .\) since \(9=9,\) the \(L H S=R H S\) and \(x=-2\) is a solution to the equation.
Check whether \(x=-6\) is a solution of the equation
\[10+10 x=13+6(x+1) ?\nonumber\]
- Answer
-
No, since the LHS is \(10+10(-6)=-50\) but the RHS is \(13+6(-6+1)=-17\).
Interactive Exercise \(\PageIndex{7}\)
To solve an equation means to find all the solution(s) for that equation. The method to solve an equation depends on the kind of equation at hand. For example, we solve linear equations by isolating the variable and quadratic equations by using the quadratic formula.
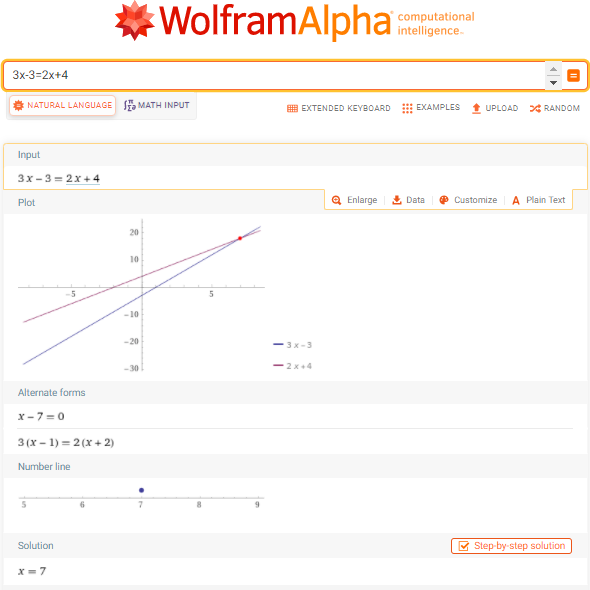
Solve the equation \(3x − 3 = 2x + 4\) for \(x\).
Solution
We will isolate all terms containing an \(x\) on the left side of this equation (we could just as well have chosen to isolate terms containing x on the right side of the equation). To this end, we don’t want the −3 on the left side of the equation (we want it on the right), so we add 3 to both sides of the equation and simplify.
\[\begin{aligned} 3 x-3 &=2 x+4 \\ 3 x-3+3 &=2 x+4+3 \\ 3 x &=2 x+7 \end{aligned}\]
Remember that we have chosen to isolate all terms containing x on the left side of the equation. So, for our next step, we choose to subtract 2x from both sides of the equation (this will “move” it from the right over to the left), then simplify.
\[\begin{aligned} 3 x &=2 x+7 \\ 3 x-2 x &=2 x+7-2 x \\ x &=7 \end{aligned}\]
To check the solution, substitute x = 7 in the original equation to obtain
\[\begin{aligned} 3 x-3 &=2 x+4 \\ 3(7)-3 &=2(7)+4 \\ 21-3 &=14+4 \\ 18 &=18 \end{aligned}\]
The last line is a true statement, so \(x = 7\) checks and is a solution of \(3x − 3 = 2x + 4\).
Solve the equation \(x + 3 = x^2 - 2\) for \(x\).
Solution
Collect all the terms on the left side:
\[\begin{aligned} x^2-x-5=0\end{aligned}\]
Apply the quadratic formula:
\[\begin{aligned} x&=\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot 1\cdot(-5)}}{2}\\&=\frac{1\pm\sqrt{21}}{2}\end{aligned}\]
Interactive Exercise \(\PageIndex{8}\)
Solving Equations with Technology
Luckily, when it comes to solving equations, we can trust technology with performing this task. Instead of isolating the variable by hand or using the quadratic formula, let's discuss how technology can be used.
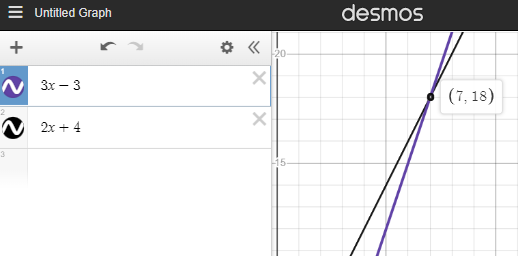
In Desmos Graphing Calculator, enter the expression on the left side of the equation then press Enter and enter the expression on the right side of the equation. The graphs will appear on the coordinate plane representing the sides of the equation. The x-coordinates of the points of intersection are the solutions of the equation. For example, solving the equation \(3x-3=2x+4\) in Example \(\PageIndex{8}\) is shown below:
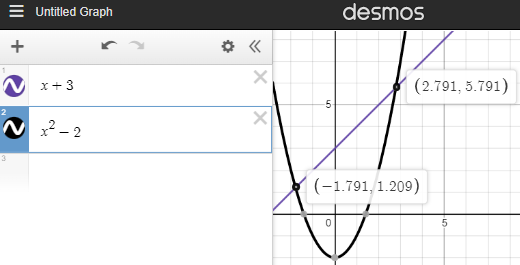
For example, solving the equation \(x+3=x^2-2\) in Example \(\PageIndex{9}\) is shown below:
In WolframAlpha, enter the equation and press Enter. Along with many other things associated with the equation you will find the solution at the very bottom of the output page. For example, solving the equation \(3x-3=2x+4\) in Example \(\PageIndex{8}\) is shown below:
For example, solving the equation \(x+3=x^2-2\) in Example \(\PageIndex{9}\) is shown below:
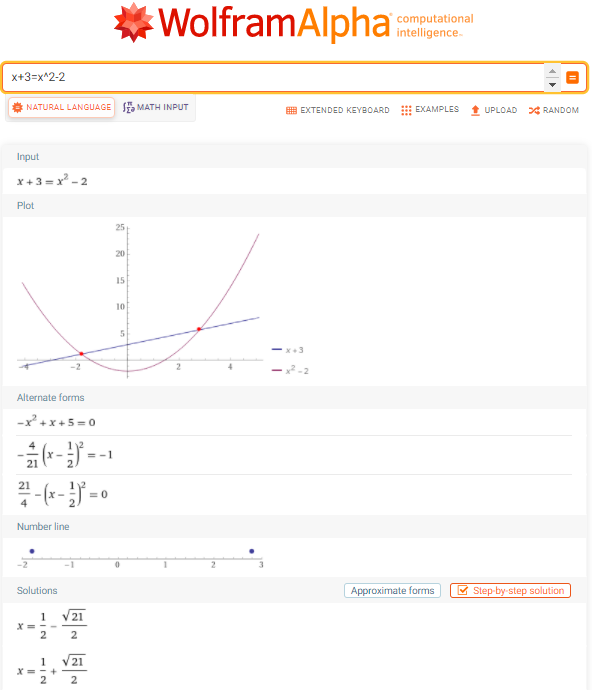
The main difference between WolframAlpha and Desmos is that WolframAlpha can provide the exact solutions (in case of solving quadratic equation \(x+3=x^2-2\), \(x=1/2\pm\frac{\sqrt{21}}{2}\)) while Desmos can only do an approximation (in case of solving quadratic equation \(x+3=x^2-2\), \(x=−1.791\) or \(2.791\)). WolframAlpha in general is a more powerful tool but for graphing purposes, Desmos is great enough.
Using Formulas
A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. In other words, a formula can be converted to an equation in one variable if the values are provided for all but one variable. One of the most common examples is the formula for finding the area \(A\) of a circle in terms of the radius \(r\) of the circle: \( A= \pi r^2\). For any value of \(r\), the area \(A\) can be found by evaluating the expression \(\pi r^2\). On the other hand, for any value of \(A\), the radius \(r\) can be found by solving the equation. For example, if \(A=6\) then the quadratic equation that needs to be solved is \(\pi r^2=6\).
A right circular cylinder with radius \(r\) and height \(h\) has the surface area \(S\) (in square units) given by the formula \(S=2\pi r(r+h)\). See Figure \(\PageIndex{7}\). Find the surface area of a cylinder with radius \(6\) in. and height \(9\) in. Leave the answer in terms of \(\pi\).
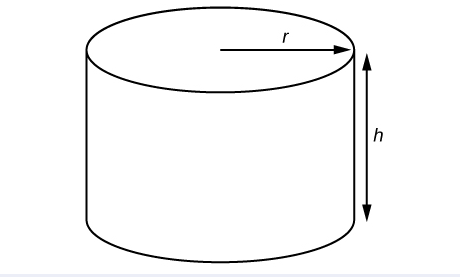
Solution
Evaluate the expression \(2\pi r(r+h)\) for \(r=6\) and \(h=9\).
\[\begin{align*} S &= 2\pi r(r+h) \\ &= 2\pi (6)[(6)+(9)] \\ &= 2\pi(6)(15) \\ &= 180\pi \end{align*}\]
The surface area is \(180\pi\) square inches.
A right circular cylinder with radius \(r\) and height \(h\) has the surface area \(S\) (in square units) given by the formula \(S=2\pi r(r+h)\). See Figure \(\PageIndex{7}\). Find the surface area of a cylinder with radius \(2\) in. and height \(5\) in. Leave the answer in terms of \(\pi\).
- Answer
-
Evaluate the expression \(2\pi r(r+h)\) for \(r=2\) and \(h=5\).
\[\begin{align*} S &= 2\pi r(r+h) \\ &= 2\pi (2)[(2)+(5)] \\ &= 2\pi(2)(7) \\ &= 28\pi \end{align*}\]
The surface area is \(28\pi\) square inches.
Interactive Exercise \(\PageIndex{10}\)
Here are some more examples of applications that come from geometry.
a) Find the perimeter of a rectangle with length \(33 \mathrm{cm}\) and width \(17 \mathrm{cm}\).
\(\begin{align*}
P &=2 l+2 w \\
&=2(33 \mathrm{cm})+2(17 \mathrm{cm}) \\
&=66 \mathrm{cm}+34 \mathrm{cm} \\
&=100 \mathrm{cm}
\end{align*}\)
b) Find the area of a rectangle that is \(12 \mathrm{cm}\) long and \(16 \mathrm{cm}\) wide.
\(\begin{align*}
A &=l \cdot w \\
&=12 \mathrm{cm} \cdot 16 \mathrm{cm} \\
&=192 \mathrm{cm}^{2}
\end{align*}\)
c) Find the area of a triangle with height of \(20 \mathrm{in}\) and a base of \(30 \mathrm{in}\).
\(\begin{align*}
A &=\frac{1}{2} b \cdot h \\
&=\frac{1}{2} 20 \mathrm{in} \cdot 30 \mathrm{in} \\
&=300 \mathrm{in}^{2}
\end{align*}\)
d) Find the area of a circle with radius \(7 \mathrm{cm},\) round your answer to the nearest tenth.
\(\begin{align*}
A &=\pi r^{2} \\
&=\pi(7 \mathrm{cm})^{2} \\
& \approx 3.14 \cdot 49 \mathrm{cm}^{2} \\
&=153.86 \mathrm{cm}^{2} \\
& \approx 153.9 \mathrm{cm}^{2}
\end{align*}\)
A photograph with length \(L\) and width \(W\) is placed in a matte of width \(8\) centimeters (cm). The area of the matte (in square centimeters, or \(cm^2\) is found to be \(A=(L+16)(W+16) - L⋅W\)
Find the area of a matte for a photograph with length \(32\) cm and width \(24\) cm. - Find the length of a photograph with the area of a matte \(1376\) sq cm and width \(30\) cm.
- Find the width of a photograph with the area of a matte \(928\) sq cm and length \(18\) cm.
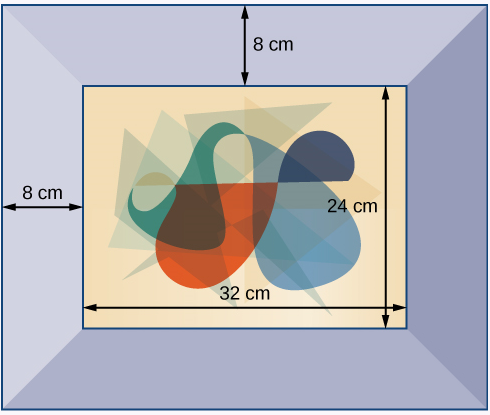
Solution
- Evaluate the expression \(A=(L+16)(W+16) - L⋅W\) for \(L=32\) and \(W=24\): \begin{align*} A&=(32+16)(24+16) - 32⋅24\\&=48⋅40-32⋅24 \\&=1152 \text{cm}^2\end{align*}
- Solve the equation \(A=(L+16)(W+16) - L⋅W\) for \(A=1376\) and \(W=30\): \begin{align*}1376&=(L+16)(30+16) - L⋅30 \\ 1376&=16L+736 \\ L&=40 \text{cm}\end{align*}
- Solve the equation \(A=(L+16)(W+16) - L⋅W\) for \(A=928\) and \(L=18\): \begin{align*}928&=(18+16)(W+16) - 18⋅W \\ 928&=16W+544 \\ W&=24 \text{cm}\end{align*}
A photograph with length \(L\) and width \(W\) is placed in a matte of width \(10\) centimeters (cm). The area of the matte (in square centimeters, or \(cm^2\) is found to be \(A=(L+20)(W+20) - L⋅W\)
Find the area of a matte for a photograph with length \(30\) cm and width \(20\) cm. - Find the length of a photograph with the area of a matte \(1600\) sq cm and width \(10\) cm.
- Find the width of a photograph with the area of a matte \(928\) sq cm and length \(18\) cm.
- Answer
-
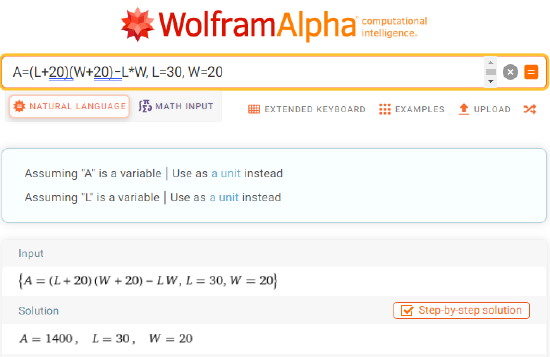
- Evaluate the expression \(A=(L+20)(W+20) - L⋅W\) for \(L=30\) and \(W=20\): \begin{align*}A&=(30+20)(20+20) - 30⋅20\\&=50⋅40-30⋅20 \\&=1400 \text{cm}^2\end{align*}
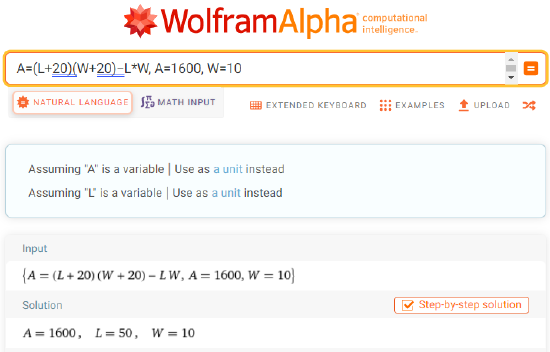
- Solve the equation \(A=(L+20)(W+20) - L⋅W\) for \(A=1600\) and \(W=10\): \begin{align*}1600&=(L+20)(10+20) - L⋅10 \\ 1600&=20L+600 \\ L&=50 \text{cm}\end{align*}
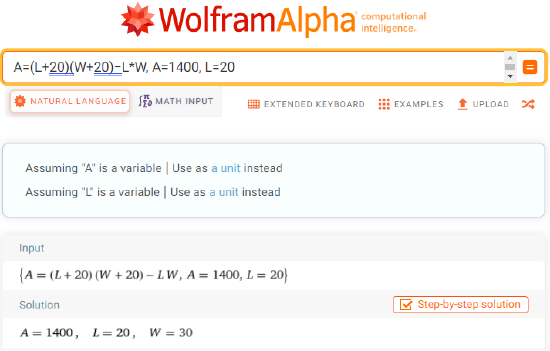
- Solve the equation \(A=(L+20)(W+20) - L⋅W\) for \(A=1400\) and \(L=20\): \begin{align*}1400&=(20+20)(W+20) - 20⋅W \\ 1400&=20W+800 \\ W&=30 \text{cm}\end{align*}
Using Formulas with Technology
Luckily, when it comes to using formulas, we can trust technology with performing this task. Instead of plugging in the values by hand, and then evaluating an expression or solving an equation let's discuss how technology can be used.
In WolframAlpha, enter the formula, followed by the variables and their assigned values separated by comma. Once the values for all involved variables are entered press Enter and WolframAlpha will determine the value of the missing variable. For example, using the formula \(A=(L+20)(W+20)−L⋅W\) for \(L=30\) and \(W=20\) in part 1 of Example \(\PageIndex{11}\) is shown below:
Similarly, using the formula \(A=(L+20)(W+20)−L⋅W\) for \(A=1600\) and \(W=10\) in part 2 of Example \(\PageIndex{11}\) is shown below:
Finally, using the formula \(A=(L+20)(W+20)−L⋅W\) for \(A=1400\) and \(L=20\) in part 3 of Example \(\PageIndex{11}\) is shown below:
Interactive Exercise \(\PageIndex{12}\)