3.6.2: Solving Basic Percent Problems

There are three basic types of percent problems:

1. Find a given percent of a given number. For example, find 25% of 640.
2. Find a percent given two numbers. For example, 15 is what percent of 50?
3. Find a number that is a given percent of another number. For example, 10% of what number is 12?

Let’s begin with the first of these types.

Find a Given Percent of a Given Number

Let’s begin with our first example.

Example 1

What number is 25% of 640?

Solution

Let x represent the unknown number. Translate the words into an equation.

\[ \begin{array}{c c c c c} \colorbox{cyan}{What number} & \text{ is } & \colorbox{cyan}{25%} & \text{ of } & \colorbox{cyan}{640} \\ x & = & 25 \% & \cdot & 640 \end{array}\nonumber \]

Now, solve the equation for x.

\[ \begin{aligned} x = 25 \% \cdot 640 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x = 0.25 \cdot 640 ~ & \textcolor{red}{ \text{ Change 25% to a decimal: 25% = 0.25.}} \\ x = 160 ~ & \textcolor{red}{ \text{ Multiply: 0.25 \cdot 640 = 160.}} \end{aligned}\nonumber \]

Thus, 25% of 640 is 160.

Alternate Solution

We could also change 25% to a fraction.

\[ \begin{aligned} x = 25 \% \cdot 640 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x = \frac{1}{4} \cdot 640 ~ & \textcolor{red}{ \text{ Change 25% to a fraction: 25% = 25/100 = 1/4.}} \\ x = \frac{640}{4} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ x = 160 ~ & \textcolor{red}{ \text{ Divide: 640/4 = 160.}} \end{aligned}\nonumber \]

Same answer.

Exercise

What number is 36% of 120?

Answer

43.2

Example 2

What is number \(8 \frac{1}{3} \%\) of 120?

Solution

Let x represent the unknown number. Translate the words into an equation.

\[ \begin{array}{c c c c c} \colorbox{cyan}{What number} & \text{ is } & \colorbox{cyan}{8 (1/3)%} & \text{ of } & \colorbox{cyan}{120} \\ x & = & 8 \frac{1}{3} \% & \cdot & 120 \end{array}\nonumber \]

Now, solve the equation for x. Because

\[8 \frac{1}{3} \%= 8.3 \% = 0.08 \overline{3},\nonumber \]

working with decimals requires that we work with a repeating decimal. To do so, we would have to truncate the decimal representation of the percent at some place and satisfy ourselves with an approximate answer. Instead, let’s change the percent to a fraction and seek an exact answer.

\[ \begin{aligned} 8 \frac{1}{3} \% = \frac{8 \frac{1}{3}}{100} ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{ \frac{25}{3}}{100} ~ & \textcolor{red}{ \text{ Mixed to improper fraction.}} \\ = \frac{25}{3} \cdot \frac{1}{100} ~& \textcolor{red}{ \text{ Invert and multiply.}} \\ = \frac{25}{300} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{1}{12} ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator by 25.}} \end{aligned}\nonumber \]

Now we can solve our equation for x.

\[ \begin{aligned} = 8 \frac{1}{3} \% \cdot 120 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x = \frac{1}{12} \cdot 120 ~ & \textcolor{red}{8 \frac{1}{3} \% = 1/12.} \\ x = \frac{120}{12} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ x = 10 ~ & \textcolor{red}{ \text{ Divide: 120/12 = 10.}} \end{aligned}\nonumber \]

Thus, \(8 \frac{1}{3} \%\) of 120 is 10.

Exercise

What number is \(4 \frac{1}{6} \%\) of 1,200?

Answer

50

Example 3

What number is \(105 \frac{1}{4} \%\) of 18.2?

Solution

Let x represent the unknown number. Translate the words into an equation.

\[ \begin{array}{c c c c c} \colorbox{cyan}{What number} & \text{ is } & \colorbox{cyan}{105 (1/4) %} & \text{ of } & 18.2 \\ x & = & 105 \frac{1}{4} \% & \cdot & 18.2 \end{array}\nonumber \]

In this case, the fraction terminates as 1/4=0.25, so

\[105 \frac{1}{4} \% = 105.25% = 1.0525.\nonumber \]

Now we can solve our equation for x.

\[ \begin{aligned} x = 105 \frac{1}{4} \% \cdot 18.2 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x = 1.0525 \cdot 18.2 ~ & \textcolor{red}{5 \frac{1}{4} \% = 1.0525.} \\ x = 19.1555 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Thus, \(105 \frac{1}{4} \%\) of 18.2 is 19.1555.

Exercise

What number is \(105 \frac{3}{4} \%\) of 222?

Answer

234.765

Find a Percent Given Two Numbers

Now we’ll address our second item on the list at the beginning of the section.

Example 4

15 is what percent of 50?

Solution

Let x represent the unknown percent. Translate the words into an equation.

\[ \begin{array}{c c c c} \colorbox{cyan}{15} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{50} \\ 15 & = & x & \cdot & 50 \end{array}\nonumber \]

The commutative property of multiplication allows us to change the order of multiplication on the right-hand side of this equation.

\[15 = 50x.\nonumber \]

Now we can solve our equation for x.

\[ \begin{aligned} 15 = 50x ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{15}{50} = \frac{50x}{50} ~ & \textcolor{red}{ \text{ Divide both sides by 50.}} \\ \frac{15}{50} = x ~ & \textcolor{red}{ \text{ Simplify right-hand side.}} \\ x = 0.30 ~ & \textcolor{red}{ \text{ Divide: 15/50 = 0.30.}} \end{aligned}\nonumber \]

But we must express our answer as a percent. To do this, move the decimal two places to the right and append a percent symbol.

Thus, 15 is 30% of 50.

Alternative Conversion

At the third step of the equation solution, we had

\[x = \frac{15}{50}.\nonumber \]

We can convert this to an equivalent fraction with a denominator of 100.

\[x = \frac{15 \cdot 2}{50 \cdot 2} = \frac{30}{100}\nonumber \]

Thus, 15/50 = 30/100 = 30%.

Exercise

14 is what percent of 25?

Answer

56%

Example 5

10 is what percent of 80?

Solution

Let x represent the unknown percent. Translate the words into an equation.

\[ \begin{array}{c c c c c} \colorbox{cyan}{10} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{80} \\ 10 & = & x & \cdot & 80 \end{array}\nonumber \]

The commutative property of multiplication allows us to write the right-hand side as

\[10 = 80x.\nonumber \]

Now we can solve our equation for x.

\[ \begin{aligned} 10 = 80x ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{10}{80} = \frac{80x}{80} ~ & \textcolor{red}{ \text{ Divide both sides by 80.}} \\ \frac{1}{8} = x ~ & \textcolor{red}{ \text{ Reduce: } 10/80 = 1/8.} \\ 0.125 = x ~ & \textcolor{red}{ \text{ Divide: } 1/8 = 0.125.} \end{aligned}\nonumber \]

But we must express our answer as a percent. To do this, move the decimal two places to the right and append a percent symbol.

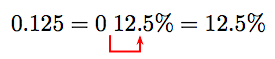
Thus, 10 is 12.5% of 80.

Alternative Conversion

At the third step of the equation solution, we had

\[x = \frac{1}{8} .\nonumber \]

We can convert this to an equivalent fraction with a denominator of 100 by setting up the proportion

\[\frac{1}{8} = \frac{n}{100}\nonumber \]

Cross multiply and solve for n.

\[ \begin{aligned} 8n = 100 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ \frac{8n}{8} = \frac{100}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ n = \frac{25}{8} ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator by 4.}} \\ n = 12 \frac{1}{2} ~ & \textcolor{red}{ \text{ Change 25/2 to mixed fraction.}} \end{aligned}\nonumber \]

Hence,

\[ \frac{1}{8} = \frac{12 \frac{1}{2}}{100} = 12 \frac{1}{2} \%.\nonumber \]

Same answer.

Exercise

10 is what percent of 200?

Answer

5%

Find a Number that is a Given Percent of Another Number

Let’s address the third item on the list at the beginning of the section.

Example 6

10% of what number is 12?

Solution

Let x represent the unknown number. Translate the words into an equation.

\[ \begin{array}{c c c c c} \colorbox{cyan}{10%} & \text{ of } & \colorbox{cyan}{what number} & \text{ is } & \colorbox{cyan}{12} \\ 10 \% & \cdot & x & = & 12 \end{array}\nonumber \]

Change 10% to a fraction: 10% = 10/100 = 1/10.

\[ \frac{1}{10} x = 12\nonumber \]

Now we can solve our equation for x.

\[ \begin{aligned} 10 \left( \frac{1}{10} x \right) = 10(12) ~ & \textcolor{red}{ \text{ Multiply both sides by 10.}} \\ x = 120 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Thus, 10% of 120 is 12.

Alternative Solution

We can also change 10% to a decimal: 10% = 0.10. Then our equation becomes

\[0.10x = 12\nonumber \]

Now we can divide both sides of the equation by 0.10.

\[ \begin{aligned} \frac{0.10x}{0.10} = \frac{12}{0.10} ~ & \textcolor{red}{ \text{ Divide both sides by 0.10.}} \\ x = 120 ~ & \textcolor{red}{ \text{ Divide: 12/0.10 = 120.}} \end{aligned}\nonumber \]

Same answer.

Exercise

20% of what number is 45?

Answer

225

Example 7

\(11 \frac{1}{9} \%\) of what number is 20?

Solution

Let x represent the unknown number. Translate the words into an equation.

\[ \begin{array}{c c c c c} \colorbox{cyan}{11 (1/9) %} & \text{ of } & \colorbox{cyan}{what number} & \text{ is } \colorbox{cyan}{20} \\ 11 \frac{1}{9} \% & \cdot & x & = & 20 \end{array}\nonumber \]

Change \(11 \frac{1}{9} \%\) to a fraction.

\[ \begin{aligned} 11 \frac{1}{9} \% ~ & \textcolor{red}{ \text{ Percent: Parts per hundred.}} \\ = \frac{ \frac{100}{9}}{100} ~ & \textcolor{red}{ \text{ Mixed to improper: } 11 \frac{1}{9} = 100/9.} \\ = \frac{100}{9} \cdot \frac{1}{100} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = \frac{ \cancel{100}}{9} \cdot \frac{1}{ \cancel{100}} ~ & \textcolor{red}{ \text{ Cancel.}} \\ = \frac{1}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Replace \(11 \frac{1}{9} \%\) with 1/9 in the equation and solve for x.

\[ \begin{aligned} \frac{1}{9} x = 20 ~ & ~ \textcolor{red}{11 \frac{1}{9} \% = 1/9/} \\ 9 \left( \frac{1}{9} x \right) = 9(20) ~ & \textcolor{red}{ \text{ Multiply both sides by 9.}} \\ x = 180 \end{aligned}\nonumber \]

Thus, \(11 \frac{1}{9} \%\) of 180 is 20.

Exercise

\(12 \frac{2}{3} \%\) of what number is 760?

Answer

6,000

Exercises

1. What number is 22.4% of 125?

2. What number is 159.2% of 125?

3. 60% of what number is 90?

4. 25% of what number is 40?

5. 200% of what number is 132?

6. 200% of what number is 208?

7. 162.5% of what number is 195?

8. 187.5% of what number is 90?

9. 126.4% of what number is 158?

10. 132.5% of what number is 159?

11. 27 is what percent of 45?

12. 9 is what percent of 50?

13. 37.5% of what number is 57?

14. 162.5% of what number is 286?

15. What number is 85% of 100?

16. What number is 10% of 70?

17. What number is 200% of 15?

18. What number is 50% of 84?

19. 50% of what number is 58?

20. 132% of what number is 198?

21. 5.6 is what percent of 40?

22. 7.7 is what percent of 35?

23. What number is 18.4% of 125?

24. What number is 11.2% of 125?

25. 30.8 is what percent of 40?

26. 6.3 is what percent of 15?

27. 7.2 is what percent of 16?

28. 55.8 is what percent of 60?

29. What number is 89.6% of 125?

30. What number is 86.4% of 125?

31. 60 is what percent of 80?

32. 16 is what percent of 8?

33. What number is 200% of 11?

34. What number is 150% of 66?

35. 27 is what percent of 18?

36. 9 is what percent of 15?

37. \(133 \frac{1}{3} \%\) of what number is 80?

38. \(121 \frac{2}{3} \%\) of what number is 73?

39. What number is \(54 \frac{1}{3} \%\) of 6?

40. What number is \(82 \frac{2}{5} \%\) of 5?

41. What number is \(62 \frac{1}{2} \%\) of 32?

42. What number is \(118 \frac{3}{4} \%\) of 32?

43. \(77 \frac{1}{7} \%\) of what number is 27?

44. \(82 \frac{2}{3} \%\) of what number is 62?

45. What number is \(142 \frac{6}{7} \%\) of 77?

46. What number is \(116 \frac{2}{3} \%\) of 84?

47. \(143 \frac{1}{2} \%\) of what number is 5.74?

48. \(77 \frac{1}{2} \%\) of what number is 6.2?

49. \(141 \frac{2}{3} \%\) of what number is 68?

50. \(108 \frac{1}{3} \%\) of what number is 78?

51. What number is \(66 \frac{2}{3} \%\) of 96?

52. What number is \(79 \frac{1}{6} \%\) of 48?

53. \(59 \frac{1}{2} \%\) of what number is 2.38?

54. \(140 \frac{1}{5} \%\) of what number is 35.05?

55. \(78 \frac{1}{2} \%\) of what number is 7.85?

56. \(73 \frac{1}{2} \%\) of what number is 4.41?

57. What number is \(56 \frac{2}{3} \%\) of 51?

58. What number is \(64 \frac{1}{2} \%\) of 4?

59. What number is \(87 \frac{1}{2} \%\) of 70?

60. What number is \(146 \frac{1}{4} \%\) of 4?

---

61. It was reported that 80% of the retail price of milk was for packaging and distribution. The remaining 20% was paid to the dairy farmer. If a gallon of milk cost $3.80, how much of the retail price did the farmer receive?

62. At $1.689 per gallon of gas the cost is distributed as follows:

\[ \begin{aligned} \text{Crude oil supplies } & ~ $0.95 \\ \text{Oil Companies } & ~ $0.23 \\ \text{State and City taxes } & ~ $0.23 \\ \text{Federal tax } & ~ $0.19 \\ \text{Service Station } & ~ $0.10 \end{aligned}\nonumber \]

Data is from Money, March 2009 p. 22, based on U. S. averages in December 2008. Answer the following questions rounded to the nearest whole percent.

a) What % of the cost is paid for crude oil supplies?

b) What % of the cost is paid to the service station?

---

Answers

1. 28

3. 150

5. 66

7. 120

9. 125

11. 60

13. 152

15. 85

17. 30

19. 116

21. 14

23. 23

25. 77

27. 45

29. 112

31. 75

33. 22

35. 150

37. 60

39. 3.26

41. 20

43. 35

45. 110

47. 4

49. 48

51. 64

53. 4

55. 10

57. 28.9

59. 61.25

61. $0.76