A person’s salary can increase by a percentage. A town’s population can decrease by a percentage. A clothing firm can discount its apparel. These are the types of applications we will investigate in this section.
Percent Increase
Example 1
Add text here.
Solution
Let x represent the salesperson’s salary increase. Then we can translate the problem into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Salary increase} & \text{ is } & \colorbox{cyan}{5%} & \text{ of } & \colorbox{cyan}{original salary} \\ x & = & 5 \% & \cdot & 4000 \end{array}\nonumber \]
Solve for x.
\[ \begin{aligned} x = 0.05 \cdot 4000 ~ & \textcolor{red}{5 \% = 0.05.} \\ x = 200 ~ & \textcolor{red}{ \text{ Multiply: 0.05 \cdot 4000 = 200.}} \end{aligned}\nonumber \]
Therefore, the salary increase is $200. To compute the new salary N, we must add this increase to the original salary.
\[ \begin{array}{c c c c c} \colorbox{cyan}{New salary} & \text{ is } & \colorbox{cyan}{original salary} & \text{ plus } & \colorbox{cyan}{increase} \\ N & = & 4000 & + & 200 \end{array}\nonumber \]
Thus, the new salary is N = $4, 200 per month.
Alternative Solution
If the salesperson is to receive a 5% increase in his salary, then his new salary will be 105% of his original salary. Let N represent his new monthly salary. Then,
\[ \begin{array}{c c c c c} \colorbox{cyan}{New salary} & \text{ is } & \colorbox{cyan}{105%} & \text{ of } & \colorbox{cyan}{original salary} \\ N & = & 105 \% & \cdot & 4000 \end{array}\nonumber \]
Solve for N.
\[ \begin{aligned} N = 1.05 \cdot 4000 ~ & \textcolor{red}{105 \% = 1.05.} \\ N = 4200 ~ & \textcolor{red}{ \text{ Multiply: } 1.05 \cdot 4000 = 4200.} \end{aligned}\nonumber \]
Same answer.
Exercise
A computer technician is granted a 4% salary increase. If the salesperson’s current salary is $2,800 per month, what will be his new salary?
- Answer
-
$2,912
Example 2
A salesperson making a salary of $4,500 per month has his salary increased to $5,000 per month. What is the percent increase?
Solution
To find the increase in salary, first subtract the original salary from the new salary.
\[ \begin{aligned} \text{ Salary increase } & \text{ = new salary − original salary} \\ ~ & = 5000 − 4500 \\ ~ & = 500 \end{aligned}\nonumber \]
Hence, the salesperson sees an increase in salary of $500.
Next, let p represent the salesperson’s percent salary increase. Then we can translate the problem into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Salary increase} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{original salary} \\ 500 & = & p & \cdot & 4500 \end{array}\nonumber \]
The commutative property of multiplication allows us to change the order of multiplication on the right-hand side of this last equation.
\[500 = 4500p\nonumber \]
Solve for p.
\[ \begin{aligned} \frac{500}{4500} = \frac{4500p}{4500} ~ & \textcolor{red}{ \text{ Divide both sides by 4500.}} \\ \frac{1}{9} = p ~ & \textcolor{red}{ \text{ Reduce by dividing numerator and denominator of 500/4500 by 500.}} \end{aligned}\nonumber \]
We need to change p = 1/9 to a percent. We can find an exact answer by creating an equivalent fraction with a denominator of 100.
\[ \begin{aligned} \frac{1}{9} = \frac{n}{100} ~ & \textcolor{red}{ \text{ Make equivalent fraction.}} \\ 9n = 100 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ \frac{9n}{9} = \frac{100}{9} ~ & \textcolor{red}{ \text{ Divide both sides by 9.}} \\ n = 11 \frac{1}{9} ~ & \textcolor{red}{ \text{ Convert 100/9 to mixed fraction.}} \end{aligned}\nonumber \]
Hence, the percent increase is
\[p = \frac{1}{9} = \frac{11 \frac{1}{9}}{100} = 11 \frac{1}{9} \%.\nonumber \]
Alternative Solution
An alternative approach is to ask what percent of the original salary equals the new salary. In this approach, let p represent the percent of the original salary that equals the new salary.
\[ \begin{array}{c c c c c} \colorbox{cyan}{New salary} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{original salary} \\ 5000 & = & p & \cdot & 4500 \end{array}\nonumber \]
Solve for p.
\[ \begin{aligned} 5000 = 4500p ~ & \textcolor{red}{ \text{ Change the order of multiplication.}} \\ \frac{5000}{4500} = \frac{4500p}{4500} ~ & \textcolor{red}{ \text{ Divide both sides by 4500.}} \\ \frac{10}{9} = p ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator of 5000/4500 by 500.}} \end{aligned}\nonumber \]
We need to change 10/9 to a percent. Again, create an equivalent fraction with a denominator of 100.
\[ \begin{aligned} \frac{10}{9} = \frac{n}{100} ~ & \textcolor{red}{ \text{ Make equivalent fraction.}} \\ 9n = 1000 ~ & \textcolor{red}{ \text{ Cross multiply.}} \\ \frac{9n}{9} = \frac{1000}{9} ~ & \textcolor{red}{ \text{ Divide both sides by 9.}} \\ n = 111 \frac{1}{9} ~ & \textcolor{red}{ \text{ Convert 1000/9 to a mixed fraction.}} \end{aligned}\nonumber \]
Thus,
\[p = \frac{10}{9} = \frac{111 \frac{1}{9}}{100} = 111 \frac{1}{9} \%.\nonumber \]
Hence, the new salary is \(111 \frac{1}{9} \%\) of the original salary. To find the percent increase, subtract 100% from \(111 \frac{1}{9} \%\).
\[111 \frac{1}{9} \% − 100 \% = 11 \frac{1}{9} \%\nonumber \]
This represents an \(11 \frac{1}{9} \%\) increase in salary, which is the same answer garnered by the first solution technique.
Exercise
A statistician making a salary of $3,200 per month has his salary increased to $3,368 per month. What is the percent increase?
- Answer
-
\(5 \frac{1}{4} \%\)
Percent Decrease
Example 3
Due to a mill closure, the population of Silvertown decreases by 8.5%. If the original population was 10,200 hardy souls, what is the new population?
Solution
Let x represent the population decrease. Then we can translate the problem into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Population decrease} & \text{ is } & \colorbox{cyan}{8.5%} & \text{ of } & \colorbox{cyan}{original population} \\ x & = & 8.5 \% & \cdot & 10200 \end{array}\nonumber \]
Solve for x.
\[ \begin{aligned} x = 0.085 \cdot 10200 ~ & \textcolor{red}{8.5 \% = 0.085.} \\ x = 867 ~ & \textcolor{red}{ \text{ Multiply: } 0.085 \cdot 10200 = 867.} \end{aligned}\nonumber \]
Therefore, the population decrease is 867. To compute the new population P, we must subtract this decrease from the original population.
\[ \begin{array}{c c c c c} \colorbox{cyan}{New population} & \text{ is } & \colorbox{cyan}{original population} & \text{ minus } & \colorbox{cyan}{population decrease} \\ P & = & 10200 & − & 867 \end{array}\nonumber \]
Thus, the new population is P = 9,333 hardy souls.
Alternative Solution
Subtract 8.5% from 100% to obtain
\[100 \% − 8.5 \% = 91.5 \%.\nonumber \]
Thus, if 8.5% of the population leaves town, then 91.5% of the population stays. Thus, the new population P is calculated from the original as follows:
\[ \begin{array}{c c c c c} \colorbox{cyan}{New population} & \text{ is } & \colorbox{cyan}{91.5%} & \text{ of } & \colorbox{cyan}{original population} \\ P & = & 91.5 \% & \cdot & 10200 \end{array}\nonumber \]
Solve for P.
\[ \begin{aligned} P = 0.915 \cdot 10200 ~ & \textcolor{red}{91.5 \% = 0.915.} \\ P = 9333 ~ & \textcolor{red}{ \text{ Multiply: } 0.915 \cdot 10200 = 9333. } \end{aligned}\nonumber \]
Same answer.
Exercise
Several retail stores close and the population of Athens decreases by 7.2% as a result. If the original population was 12,500, what is the new population?
- Answer
-
11,600
Example 4
Millertown falls on hard times and its population decreases from 11,256 to 10,923 in the space of one year. What is the percent decrease, rounded to the nearest hundredth of a percent?
Solution
To find the decrease in population, first subtract the current population from the original population.
\[ \begin{aligned} \text{ Population decrease } & = \text{ original population − current population} \\ ~ & = 11256 − 10923 \\ ~ & = 333 \end{aligned}\nonumber \]
Hence, the population has decreased by 333 people.
Next, let p represent the percent population decrease. Then we can translate the problem into words and symbols.
\[ \begin{array}{c c c c c} \colorbox{cyan}{Population decrease} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{original population} \\ 333 & = & p & \cdot & 11256 \end{array}\nonumber \]
Solve for p.
\[ \begin{aligned} \frac{333}{11256} = \frac{11256p}{11256} ~ & \textcolor{red}{ \text{ Divide both sides by 11256.}} \\ 0.02958 \approx p ~ & \textcolor{red}{ \text{ Divide: 333/11256 \approx 0.02958.}} \end{aligned}\nonumber \]
To change p to a percent, move the decimal point two places to the right and append a percent symbol.

We are asked to round to the nearest hundredth of a percent.
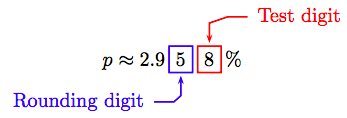
Because the test digit is greater than or equal to 5, add 1 to the rounding digit and truncate. That is,
\[p \approx 2.96 \%.\nonumber \]
Thus, the population of Millertown decreases approximately 2.96%.
Alternative Solution
An alternative approach is to ask what percent of the original population equals the new population.
\[ \begin{array}{c c c c c} \colorbox{cyan}{New population} & \text{ is } & \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{original population} \\ 10923 & = & p & \cdot & 11256 \end{array}\nonumber \]
Solve for p.
\[ \begin{aligned} 10923 = 11256p ~ & \textcolor{red}{ \text{ Change the order of multiplication.}} \\ \frac{10923}{11256} = \frac{11256p}{11256} ~ & \textcolor{red}{ \text{ Divide both sides by 11256.}} \\ 0.97041 \approx p ~ & \textcolor{red}{ \text{ Divide: } 10923/11256 \approx 0.97041.} \end{aligned}\nonumber \]
To change p to a percent, move the decimal two places to the right and append a percent symbol.

We are asked to round to the nearest hundredth of a percent.
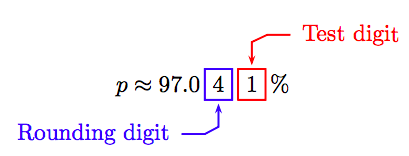
Because the test digit is less than 5, leave the rounding digit alone and truncate. That is,
\[p \approx 97.04 \%.\nonumber \]
Thus, 97.04% of the Millertown population remains. To find the percent decrease (the percent who left), subtract 97.04% from 100%.
\[100 \% − 97.04 \% = 2.96 \%\nonumber \]
Hence, the population of Millertown decreases by 2.96%. Same answer.
Exercise
A textile mill closure results in the population of the adjacent town decreasing from 8,956 to 7,800. What is the percent decrease in the population, rounded to the nearest tenth of a percent?
- Answer
-
12.9%
Discount
Another important application of percent is the discounting of goods.
Example 5
A pair of skis is marked at $310. However, a sign in the shop indicates that skis are being discounted at 15%. What will be the new selling price of the skis?
Solution
Let D represent the discount (in dollars) given for our pair of skis. Then, in words and symbols:
\[ \begin{array}{c c c c c} \colorbox{cyan}{Discount} & \text{ is } & \colorbox{cyan}{15%} & \text{ of } & \colorbox{cyan}{original marked price} \\ D & = & 15 \% & \cdot & 310 \end{array}\nonumber \]
Solve for D.
\[ \begin{aligned} D = 0.15 \cdot 310 ~ & ~ \textcolor{red}{ 15 \% = 0.15.} \\ D = 46.50 ~ & ~ \textcolor{red}{ \text{ Multiply: } 0.15 \cdot 310 = 46.50.} \end{aligned}\nonumber \]
Hence, the discount is $46.50. To find the new selling price, subtract this discount from the original selling price.
\[ \begin{aligned} \text{New selling price } & \text{ = original selling price − discount} \\ ~ & ~ = 310 − 46.50 \\ & ~ = 263.50 \end{aligned}\nonumber \]
Hence, the new selling price is $263.50.
Alternate Solution
Subtract 15% from 100% to obtain
\[100 \% − 15 \% = 85 \%.\nonumber \]
That is, if an item is discounted 15%, then its new selling price S is 85% of its original marked price.
\[ \begin{array}{c c c c c} \colorbox{cyan}{New selling price} & \text{ is } & \colorbox{cyan}{85%} & \text{ of } & \colorbox{cyan}{original marked price} \\ S & = & 85 \% & \cdot & 310 \end{array}\nonumber \]
Solve for S.
\[ \begin{aligned} S = 0.85 \cdot 310 ~ & \textcolor{red}{ ~ 85 \% = 0.85.} \\ S = 263.50 ~ & \textcolor{red}{ \text{ Multiply: } 0.85 \cdot 310 = 263.50.} \end{aligned}\nonumber \]
Thus, the new selling price is $263.50. Same answer.
Exercise
A pair of hiking boots is marked at $200. During a sale, the boots are discounted by 8%. What is the new price of the boots?
- Answer
-
$184
Example 6
A pair of ski boots marked at $210 is sold for $180. Find the percent discount, correct to the nearest tenth of a percent.
Solution
We can find the discount (in dollars) by subtracting the sale price from the original marked price.
\[ \begin{aligned} \text{Discount } & \text{ = original marked price − sale price} \\ ~ & ~ = 210 − 180 \\ ~ & ~ = 30 \end{aligned}\nonumber \]
Hence, the boots are discounted $30.
Let p represent the percent discount. Then, in words and symbols:
\[ \begin{array}{c c c c c} \colorbox{cyan}{Discount} & \text{ is } & \colorbox{cyan}{percent discount} & \text{ of } & \colorbox{cyan}{ original marked price} \\ 30 & = & p & \cdot & 210 \end{array}\nonumber \]
Solve for p.
\[ \begin{aligned} 30 = 210p ~ & \textcolor{red}{ \text{ Change order of multiplication.}} \\ \frac{30}{210} = \frac{210p}{210} ~ & \textcolor{red}{ \text{ Divide both sides by 210.}} \\ \frac{1}{7} = p ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator of 30/210 by 30.}} \\ p \approx ~ & \textcolor{red}{ \text{ Divide: 1/7 } \approx 0.1428.} \end{aligned}\nonumber \]
To change p to a percent, move the decimal point two places to the right and append a percent symbol.

Round to the nearest tenth of a percent.
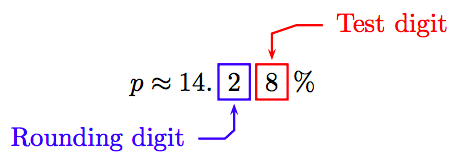
Because the test digit is greater than or equal to 5, add 1 to the rounding digit and truncate. Thus, correct to the nearest tenth of a percent, the percent discount is
\[p \approx 14.3 \%.\nonumber \]
Alternate Solution
An alternative approach is to ask what percent p of the original marked price equals the selling price.
\[ \begin{array}{c c c c c} \colorbox{cyan}{New selling price} & \text{ is } \colorbox{cyan}{what percent} & \text{ of } & \colorbox{cyan}{original marked price} \\ 180 & = & p & \cdot & 210 \end{array}\nonumber \]
Solve for p.
\[ \begin{aligned} 180 = 210p ~ & \textcolor{red}{ \text{ Change the order of multiplication.}} \\ \frac{180}{210} = \frac{210p}{210} ~ & \textcolor{red}{ \text{ Divide both sides by 210.}} \\ \frac{6}{7} = p ~ & \textcolor{red}{ \text{ Reduce: Divide numerator and denominator of 180/210 by 30.}} \\ p \approx ~ & \textcolor{red}{ \text{ Divide: } 6/7 \approx 0.8571.} \end{aligned}\nonumber \]
To change p to a percent, move the decimal point two places to the right and append a percent symbol.

Round to the nearest tenth of a percent.
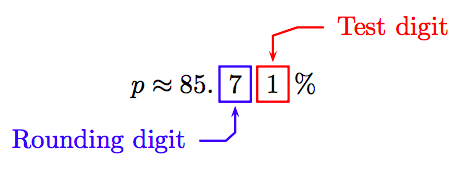
Because the test digit is less than 5, do nothing to the rounding digit and truncate. Thus, correct to the nearest tenth of a percent,
\[p \approx 85.7 \%.\nonumber \]
Thus, the new selling price is 85.7% of the original marked price. Subtract 85.7% from 100%.
\[100 \% − 85.7 \% = 14.3 \%.\nonumber \]
That is, if the new selling price is 85.7% of the original price, then the percent discount is 14.3%. This is the same answer found with the first method.
Exercise
A computer marked at $2,000 is sold at a discount for $1,850. Find the percent discount, correct to the nearest tenth of a percent.
- Answer
-
7.5%
Exercises
1. A television set is marked at $447. However, a sign in the shop indicates that the television set is being discounted at 20.5%. What will be the new selling price of the television set? Round your answer to the nearest penny.
2. A stereo set is marked at $380. However, a sign in the shop indicates that the stereo set is being discounted at 7.5%. What will be the new selling price of the stereo set? Round your answer to the nearest penny.
3. Due to a ball bearing plant closure, Anselm falls on hard times and its population decreases from 10,794 to 8,925 in the space of one year. What is the percent decrease, rounded to the nearest hundredth of a percent?
4. Due to a logging mill closure, Carlytown falls on hard times and its population decreases from 12,113 to 10,833 in the space of one year. What is the percent decrease, rounded to the nearest hundredth of a percent?
5. A car rack is marked at $500. However, a sign in the shop indicates that the car rack is being discounted at 3.5%. What will be the new selling price of the car rack? Round your answer to the nearest penny.
6. A car rack is marked at $405. However, a sign in the shop indicates that the car rack is being discounted at 17.5%. What will be the new selling price of the car rack? Round your answer to the nearest penny.
7. Due to a textile mill closure, the population of Silvertown decreases by 4.1%. If the original population was 14,678 hardy souls, what is the new population, correct to the nearest person?
8. Due to a department store closure, the population of Petroria decreases by 5.3%. If the original population was 14,034 hardy souls, what is the new population, correct to the nearest person?
9. A bartender is granted a 4.6% salary increase. If the bartender’s current salary is $2,500 per month, find the bartender’s new monthly salary, rounded to the nearest dollar.
10. A bartender is granted a 5.5% salary increase. If the bartender’s current salary is $2,900 per month, find the bartender’s new monthly salary, rounded to the nearest dollar.
11. A car rack marked at $358 is sold for $292. Find the percent discount, correct to the nearest tenth of a percent.
12. A bicycle marked at $328 is sold for $264. Find the percent discount, correct to the nearest tenth of a percent.
13. Due to a auto manufacturing plant closure, Carlytown falls on hard times and its population decreases from 14,393 to 12,623 in the space of one year. What is the percent decrease, rounded to the nearest hundredth of a percent?
14. Due to a ball bearing plant closure, Mayville falls on hard times and its population decreases from 8,494 to 6,609 in the space of one year. What is the percent decrease, rounded to the nearest hundredth of a percent?
15. Due to a auto manufacturing plant closure, the population of Silvertown decreases by 2.4%. If the original population was 8,780 hardy souls, what is the new population, correct to the nearest person?
16. Due to a textile mill closure, the population of Ghosttown decreases by 6.1%. If the original population was 14,320 hardy souls, what is the new population, correct to the nearest person?
17. A clerk making a salary of $2,600 per month has her salary increased to $2,950 per month. Find the percent increase correct to the nearest tenth of a percent.
18. A clerk making a salary of $3,600 per month has her salary increased to $4,100 per month. Find the percent increase correct to the nearest tenth of a percent.
19. A bartender making a salary of $4,200 per month has her salary increased to $4,300 per month. Find the percent increase correct to the nearest tenth of a percent.
20. A bartender making a salary of $3,200 per month has her salary increased to $3,550 per month. Find the percent increase correct to the nearest tenth of a percent.
21. A gardener is granted a 5.1% salary increase. If the gardener’s current salary is $3,200 per month, find the gardener’s new monthly salary, rounded to the nearest dollar.
22. A secretary is granted a 2.8% salary increase. If the secretary’s current salary is $3,600 per month, find the secretary’s new monthly salary, rounded to the nearest dollar.
23. A television set marked at $437 is sold for $347. Find the percent discount, correct to the nearest tenth of a percent.
24. A camera marked at $390 is sold for $328. Find the percent discount, correct to the nearest tenth of a percent.
25. Suppose that the price of an 8-ounce can of tomato sauce increased from $0.20 to $0.28.
a) What was the amount of increase?
b) What was the percent increase?
26. The following table summarizes summertime gasoline prices in San Francisco, CA. The price is the number of dollars required to purchase one gallon of unleaded gasoline. Data from gasbuddy.com.
\[ \begin{array}{ c c} \text{Year } & \text{ Price per gallon} \\ 2003 & 1.80 \\ 2004 & 2.28 \\ 2005 & 2.57 \\ 2006 & 3.20 \\ 2007 & 3.28 \\ 2008 & 4.61 \\ 2009 & 3.01 \end{array}\nonumber \]
What is the percent increase or decrease from 2003 to 2005? Round your answer to the nearest whole percent.
27. Refer to the table of gas prices in Exercise 26. What is the percent increase or decrease from 2005 to 2007? Round your answer to the nearest whole percent.
28. Refer to the table of gas prices in Exercise 26. What is the percent increase or decrease from 2007 to 2009? Round your answer to the nearest whole percent.
29. Rate hike. A family paying $858 monthly for health coverage is faced with a 39% hike in rates. What will be their new monthly cost after the increase? Associated Press-Times-Standard 02/09/10 HHS secretary asks Anthem Blue Cross to justify rate hike.
30. Parking fine. San Francisco’s Metropolitan Transportation Agency was expected to consider raising fines for the use of fake, stolen, or borrowed disabled parking tags from $100 to $825. What is the percent increase for this fine? Associated Press-Times-Standard 01/06/10 Fines for fake disabled parking tags may go up in San Francisco.
31. Industrial move. Regulations in California have caused factory farmers to move out of state. Idaho’s industrial dairy went from 180, 000 cows in 1990 to 530, 000 cows in 2009. What is the percent increase for Idaho industrial dairy cows, rounded to the nearest percent? Associated Press-Times-Standard 02/09/10 Idaho, others prepare for California egg farm exodus.
32. Whooping crane. Whooping crane populations made a remarkable comeback from just 15 birds in 1941 to about 400 birds worldwide in 2010. What is the percent increase for the whooping crane population over the past seventy years, rounded to the nearest percent? Associated Press-Times-Standard 03/17/10 Plucky whooping crane gives wildlife experts hope.
33. Underwater. The loss of Arctic sea ice will allow for an underwater fiber optic cable that will cut the time it takes to send a message from London to Tokyo from a current 140 milliseconds down to 88 milliseconds. Associated Press-Times-Standard 01/22/10 Global warming opens up Northwest Passage for underwater fiber optic cable.
a) What is the estimated percent decrease in communication time?
b) At a cost of $1.2 billion, what is the cost per millisecond of saving (rounded to the nearest dollar)?
34. Chinook salmon. During the 2009 season in the Sacramento river basin, a record low 39,500 chinook salmon were recorded, way down from the more than 750,000 counted in 2002. What is the percent decrease in the salmon count from 2002 to 2009, rounded to the nearest percent? Associated Press-Times-Standard 02/25/10 Feds predict better year for California salmon.
35. Daylight hours. In middle latitudes, summer days can have as many as 14 hours of daylight, while winter days can have a few as 10 hours of daylight. What percent more daylight is there in summer than in winter?
36. Cyber-experts. Defense Secretary Robert Gates said the Pentagon will increase the number of cyber-experts it can train each year from 80 to 250 by 2011. What percent increase is this? Round your answer to the nearest percent. Associated Press Times-Standard 4/19/09
37. Home prices. Real estate data for Humboldt County, California, is given below. Associated Press-Times-Standard 01/17/10 How is our local real estate market compared to other regions?
\[ \begin{array}{c c c} \text{Year } & \text{ Number of homes sold } & \text{ Average home price } \\ 2000 & 1,358 & $152,257 \\ 2005 & 1,432 & $344,500 \\ 2009 & 833 & $285,000 \end{array}\nonumber \]
a) What percent change in average home price occurred between 2000 and 2009?
b) What percent change in homes sold occurred between 2000 and 2009?










