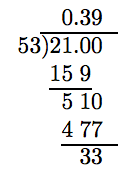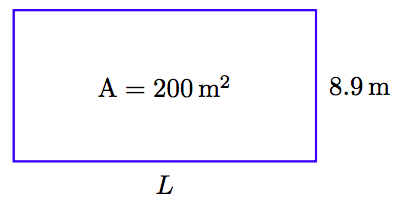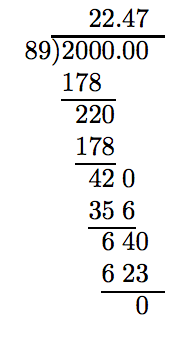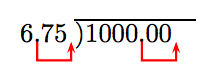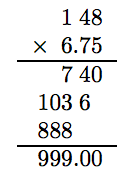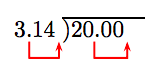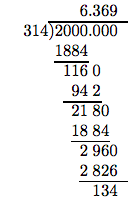We can add or subtract the same decimal number from both sides of an equation without affecting the solution.
We can still multiply both sides of an equation by the same decimal number without affecting the solution.
We can still divide both sides of an equation by the same decimal number without affecting the solution.
Rounding Solutions
Sometimes an approximate solution is adequate.
Example \(\PageIndex{1}\)
Solve the equation \(3.1x+ 4.6=2.5 − 2.2x\) for x. Round the answer to the nearest tenth.
Solution
We need to isolate the terms containing x on one side of the equation. We begin by adding 2.2x to both sides of the equation.
\[ \begin{aligned} 3.1x + 4.6 = 2.5 - 2.2x ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3.1x + 4.6 + 2.2x = 2.5 - 2.2x + 2.2x ~ & \textcolor{red}{ \text{ Add } 2.2x \text{ to both sides.}} \\ 5.3x + 4.6 = 2.5 ~ & \textcolor{red}{ \text{ Combine terms: } 3.1x + 2.2x = 5.3x.} \end{aligned{\nonumber \]
We need to isolate the terms containing x on one side of the equation. We begin by adding 2.2x to both sides of the equation.
\[ \begin{aligned} 5.3x + 4.6 - 4.6 = 2.5 - 4.6 ~ & \textcolor{red}{ \text{ Subtract 4.6 from both sides.}} \\ 5.3x = -2.1 ~ & \textcolor{red}{ \text{ Simplify: } 2.5 - 4.6 = -2.1.} \end{aligned}\nonumber \]
To undo the effect of multiplying by 5.3, divide both sides of the equation by 5.3.
\[ \begin{aligned} \frac{5.3x}{5.3} = \frac{-2.1}{5.3} ~ & \textcolor{red}{ \text{Divide both side by 5.3.}} \\ x \approx -0.4 ~ & \textcolor{red}{ \text{ Round solution to nearest tenth.}} \end{aligned}\nonumber \]
To round the answer to the nearest tenth, we must carry the division out one additional place.
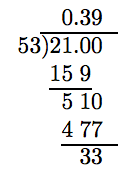
Because the “test digit” is greater than or equal to 5, add 1 to the rounding digit and truncate.
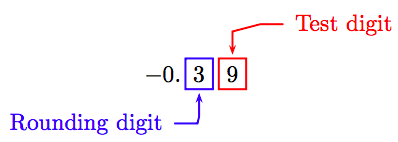
Thus, −0.39 ≈ −0.4.
Thus, −2.1/5.3 ≈ −0.39.
Exercise
Solve for x: \(4.2x − 1.25 = 3.4+0.71x\)
- Answer
-
1.33
Applications
Let’s look at some applications that involve equations containing decimals. For convenience, we repeat the Requirements for Word Problem Solutions.
Requirements for Word Problem Solutions
- Set up a Variable Dictionary. You must let your readers know what each variable in your problem represents. This can be accomplished in a number of ways:
- Statements such as “Let P represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
- Set up an Equation. Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
- Solve the Equation. You must always solve the equation set up in the previous step.
- Answer the Question. This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units.
- Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”
Let’s start with a rectangular garden problem.
Example 9
Molly needs to create a rectangular garden plot covering 200 square meters (200 m2). If the width of the plot is 8.9 meters, find the length of the plot correct to the nearest tenth of a meter.
Solution
We will follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We will use a sketch to define our variables.
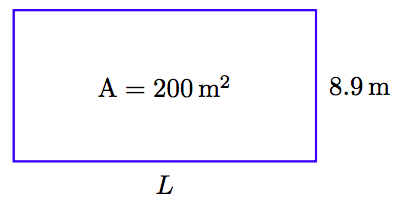
Note that L represents the length of the rectangle.
2. Set Up an Equation. The area A of a rectangle is given by the formula
\[A = LW,\nonumber \]
where L and W represent the length and width of the rectangle, respectively. Substitute 200 for A and 8.9 for W in the formula to obtain
\[200 = L(8.9),\nonumber \]
or equivalently,
\[200 = 8.9L.\nonumber \]
3. Solve the Equation. Divide both sides of the last equation by 8.9, then round your answer to the nearest tenth.
\[ \begin{aligned} \frac{200}{8.9} = \frac{8.9L}{8.9} ~ & \textcolor{red}{ \text{ Divide both sides by 8.9.}} \\ 22.5 \approx L ~ & \textcolor{red}{ \text{ Round to nearest tenth.}} \end{aligned}\nonumber \]
To round the answer to the nearest tenth, we must carry the division out one additional place.
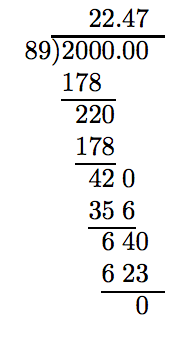
Because the “test digit” is greater than or equal to 5, add 1 to the rounding digit and truncate.
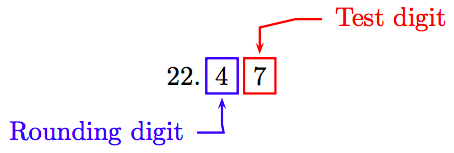
Thus, 200/8.9 ≈ 22.5.
4. Answer the Question. To the nearest tenth of a meter, the length of the rectangular plot is L ≈ 22.5 meters.
5. Look Back. We have L ≈ 22.5 meters and W = 8.9 meters. Multiply length and width to find the area.
\[\text{Area} \approx (22.5 \text{ m})(8.9 \text{ m}) ≈ 200.25 \text{ m}^2.\nonumber \]
Note that this is very nearly the exact area of 200 square meters. The discrepancy is due to the fact that we found the length rounded to the nearest tenth of a meter
Exercise
Eta’s dog run is in the shape of a rectangle with area 500 square feet. If the length of the run is 28 feet, find the width of the run, correct to the nearest tenth of a foot.
- Answer
-
17.9 feet
Example 10
Children’s tickets to the circus go on sale for $6.75. The Boys and Girls club of Eureka has $1,000 set aside to purchase these tickets. Approximately how many tickets can the Girls and Boys club purchase?
Solution
We will follow the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. Let N represent the number of tickets purchased by the Boys and Girls club of Eureka.
2. Set Up an Equation. Note that
\[ \begin{matrix} \colorbox{cyan}{Price per ticket} & \text{ times } & \colorbox{cyan}{Number of tickets} & \text{ is } & \colorbox{cyan}{Full Purchase Price} \\ 6.75 & . & N & = & 1,000 \end{matrix}\nonumber \]
Hence, our equation is 6.75N = 1000.
3. Solve the Equation. Divide both sides of the equation by 6.75.
\[ \begin{aligned} \frac{6.75N}{6.75} = \frac{1000}{6.75} ~ & \textcolor{red}{ \text{ Divide both sides by 6.75.}} \\ N \approx 148 ~ & \textcolor{red}{ \text{ Truncate to nearest unit.}} \end{aligned}\nonumber \]
Push the decimal point to the right-end of the divisor and the decimal point in the dividend an equal number of places.
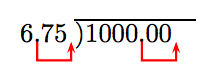
We’ll stop the division at the units position.

4. Answer the Question. The Boys and Girls club can purchase 148 tickets.
5. Look Back. Let’s calculate the cost of 148 tickets at $6.75 apiece.
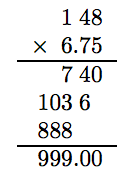
Thus, at $6.75 apiece, 148 tickets will cost $999. Because the Boys and Girls club of Eureka has $1,000 to work with, note that the club doesn’t have enough money left for another ticket.
Exercise
Adult tickets to the circus cost $12.25 apiece. If the club has $1,200 set aside for adult ticket purchase, how many adult tickets can they purchase?
- Answer
-
97
Example 11
Marta has 20 feet of decorative fencing which she will use for the border of a small circular garden. Find the diameter of the circular garden, correct to the nearest hundredth of a foot. Use π ≈ 3.14.
Solution
The formula governing the relation between the circumference and diameter of a circle is
\[C = \pi d\nonumber \]
The 20 feet of decorative fencing will be the circumference of the circular garden. Substitute 20 for C and 3.14 for π.
\[20 = 3.14d\nonumber \]
Divide both sides of the equation by 3.14.
\[ \begin{aligned} \frac{20}{3.14} = \frac{3.14d}{3.14} \\ \frac{20}{3.14} = d \end{aligned}\nonumber \]
Move the decimal point to the end of the divisor, then move the decimal point in the dividend an equal number of places (two places) to the right. Note that we must add two trailing zeros in the dividend.
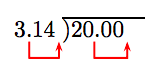
Thus, the problem becomes:
\[ 314 \overline{ )2000}\nonumber \]
We need to round to the nearest hundredth. This requires that we carry the division one additional place to the right of the hundredths place (i.e., to the thousandths place).
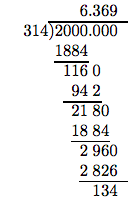
For the final step, we must round 6.369 to the nearest hundredth. In the schematic that follows, we’ve boxed the hundredths digit (the “rounding digit”) and the “test digit” that follows the “rounding digit.”
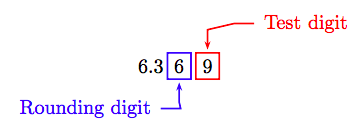
Because the “test digit” is greater than or equal to 5, we add 1 to the “rounding digit,” then truncate. Therefore, to the nearest hundredth of a foot, the diameter of the circle is approximately
\[d ≈ 6.37 \text{ ft.}\nonumber \]
Exercise
Dylan has a circular dog pen with circumference 100 feet. Find the radius of the pen, correct to the nearest tenth of a foot. Use π ≈ 3.14.
- Answer
-
15.9 feet
Exercises
In Exercises 1-16, solve the equation.
1. \(5.57x − 2.45x = 5.46\)
2. \(−0.3x − 6.5x = 3.4\)
3. \(−5.8x + 0.32 + 0.2x = −6.96\)
4. \(−2.2x − 0.8 − 7.8x = −3.3\)
5. \(−4.9x + 88.2 = 24.5\)
6. \(−0.2x − 32.71 = 57.61\)
7. \(0.35x − 63.58 = 55.14\)
8. \(−0.2x − 67.3 = 93.5\)
9. \(−10.3x + 82.4=0\)
10. \(−1.33x − 45.22 = 0\)
11. \(−12.5x + 13.5=0\)
12. \(44.15x − 8.83 = 0\)
13. \(7.3x − 8.9 − 8.34x = 2.8\)
14. \(0.9x + 4.5 − 0.5x = 3.5\)
15. \(−0.2x + 2.2x = 6.8\)
16. \(−7.9x + 2.9x = 8.6\)
In Exercises 17-34, solve the equation.
17. \(6.24x − 5.2=5.2x\)
18. \(−0.6x + 6.3=1.5x\)
19. \(−0.7x − 2.4 = −3.7x − 8.91\)
20. \(3.4x − 4.89 = 2.9x + 3.6\)
21. \(−4.9x = −5.4x + 8.4\)
22. \(2.5x = 4.5x + 5.8\)
23. \(−2.8x = −2.3x − 6.5\)
24. \(1.2x = 0.35x − 1.36\)
25. \(−2.97x − 2.6 = −3.47x + 7.47\)
26. \(−8.6x − 2.62 = −7.1x + 8.54\)
27. \(−1.7x = −0.2x − 0.6\)
28. \(3.89x = −5.11x + 5.4\)
29. \(−1.02x + 7.08 = −2.79x\)
30. \(1.5x − 2.4=0.3x\)
31. \(−4.75x − 6.77 = −7.45x + 3.49\)
32. \(−1.2x − 2.8 = −0.7x − 5.6\)
33. \(−4.06x − 7.38 = 4.94x\)
34. \(−4.22x + 7.8 = −6.3x\)
In Exercises 35-52, solve the equation.
35. \(2.3+0.1(x + 2.9) = 6.9\)
36. \(−6.37 + 6.3(x + 4.9) = −1.33\)
37. \(0.5(1.5x − 6.58) = 6.88\)
38. \(0.5(−2.5x − 4.7) = 16.9\)
39. \(−6.3x − 0.4(x − 1.8) = −16.03\)
40. \(−2.8x + 5.08(x − 4.84) = 19.85\)
41. \(2.4(0.3x + 3.2) = −11.4\)
42. \(−0.7(0.2x + 5.48) = 16.45\)
43. \(−0.8(0.3x + 0.4) = −11.3\)
44. \(7.5(4.4x + 7.88) = 17.19\)
45. \(−7.57 − 2.42(x + 5.54) = 6.95\)
46. \(5.9 − 0.5(x + 5.8) = 12.15\)
47. \(−1.7 − 5.56(x + 6.1) = 12.2\)
48. \(−7.93 + 0.01(x + 7.9) = 14.2\)
49. \(4.3x − 0.7(x + 2.1) = 8.61\)
50. \(1.5x − 4.5(x + 4.92) = 15.6\)
51. \(−4.8x + 3.3(x − 0.4) = −7.05\)
52. \(−1.1x + 1.3(x + 1.3) = 19.88\)
In Exercises 53-58, solve the equation.
53. \(0.9(6.2x − 5.9) = 3.4(3.7x + 4.3) − 1.8\)
54. \(0.4(−4.6x+ 4.7) = −1.6(−2.2x+ 6.9)−4.5\)
55. \(−1.8(−1.6x + 1.7) = −1.8(−3.6x − 4.1)\)
56. \(−3.3(−6.3x + 4.2) − 5.3=1.7(6.2x + 3.2)\)
57. \(0.9(0.4x + 2.5) − 2.5 = −1.9(0.8x + 3.1)\)
58. \(5.5(6.7x + 7.3) = −5.5(−4.2x + 2.2)\)
59. Stacy runs a business out of her home making bird houses. Each month she has fixed costs of $200. In addition, for each bird house she makes, she incurs an additional cost of $3.00. If her total costs for the month were $296.00, how many bird houses did she make?
60. Stella runs a business out of her home making curtains. Each month she has fixed costs of $175. In addition, for each curtain she makes, she incurs an additional cost of $2.75. If her total costs for the month were $274.00, how many curtains did she make?
61. A stationary store has staplers on sale for $1.50 apiece. A business purchases an unknown number of these and the total cost of their purchase is $36.00. How many were purchased?
62. A stationary store has CD packs on sale for $2.50 apiece. A business purchases an unknown number of these and the total cost of their purchase is $40.00. How many were purchased?
63. Julie runs a business out of her home making table cloths. Each month she has fixed costs of $100. In addition, for each table cloth she makes, she incurs an additional cost of $2.75. If her total costs for the month were $221.00, how many table cloths did she make?
64. Stella runs a business out of her home making quilts. Each month she has fixed costs of $200. In addition, for each quilt she makes, she incurs an additional cost of $1.75. If her total costs for the month were $280.50, how many quilts did she make?
65. Marta has 60 feet of decorative fencing which she will use for the border of a small circular garden. Find the diameter of the circular garden, correct to the nearest hundredth of a foot. Use π ≈ 3.14.
66. Trinity has 44 feet of decorative fencing which she will use for the border of a small circular garden. Find the diameter of the circular garden, correct to the nearest hundredth of a foot. Use π ≈ 3.14.
67. Children’s tickets to the ice capades go on sale for $4.25. The YMCA of Sacramento has $1,000 set aside to purchase these tickets. Approximately how many tickets can the YMCA of Sacramento purchase?
68. Children’s tickets to the ice capades go on sale for $5. The Knights of Columbus has $1,200 set aside to purchase these tickets. Approximately how many tickets can the Knights of Columbus purchase?
69. A stationary store has mechanical pencils on sale for $2.25 apiece. A business purchases an unknown number of these and the total cost of their purchase is $65.25. How many were purchased?
70. A stationary store has engineering templates on sale for $2.50 apiece. A business purchases an unknown number of these and the total cost of their purchase is $60.00. How many were purchased?
71. Marta has 61 feet of decorative fencing which she will use for the border of a small circular garden. Find the diameter of the circular garden, correct to the nearest hundredth of a foot. Use π ≈ 3.14.
72. Kathy has 86 feet of decorative fencing which she will use for the border of a small circular garden. Find the diameter of the circular garden, correct to the nearest hundredth of a foot. Use π ≈ 3.14.
73. Kathy needs to create a rectangular garden plot covering 100 square meters (100 m2). If the width of the plot is 7.5 meters, find the length of the plot correct to the nearest tenth of a meter.
74. Marianne needs to create a rectangular garden plot covering 223 square meters (223 m2). If the width of the plot is 8.3 meters, find the length of the plot correct to the nearest tenth of a meter.
75. Children’s tickets to the stock car races go on sale for $4.5. The Boys and Girls club of Eureka has $1,300 set aside to purchase these tickets. Approximately how many tickets can the Boys and Girls club of Eureka purchase?
76. Children’s tickets to the movies go on sale for $4.75. The Lions club of Alameda has $800 set aside to purchase these tickets. Approximately how many tickets can the Lions club of Alameda purchase?
77. Ashley needs to create a rectangular garden plot covering 115 square meters (115 m2). If the width of the plot is 6.8 meters, find the length of the plot correct to the nearest tenth of a meter.
78. Molly needs to create a rectangular garden plot covering 268 square meters (268 m2). If the width of the plot is 6.1 meters, find the length of the plot correct to the nearest tenth of a meter.
79. Crude Inventory. US commercial crude oil inventories decreased by 3.8 million barrels in the week ending June 19. If there were 353.9 million barrels the following week, what were crude oil inventories before the decline? rttnews.com 06/24/09
80. Undocumented. In 2008, California had 2.7 million undocumented residents. This is double the number in 1990. How many undocumented residents were in California in 1990? Associated Press Times-Standard 4/15/09
81. Diamonds Shining. The index of refraction n indicates the number of times slower that a light wave travels in a particular medium than it travels in a vacuum. A diamond has an index of refraction of 2.4. This is about one and one-quarter times greater than the index of refraction of a zircon. What is the index of refraction of a zircon? Round your result to the nearest tenth.