1.4: Polynomials

Preview Video for Sections 1.4 & 1.5

Fill in your notes (posted on moodle) as you actively go through this video. 

Login with LibreOne to view this question

NOTE: If you typically access ADAPT assignments through an LMS like Canvas, you should open this page there.

Login

Learning Objectives

In this section students will:

• Identify the degree and leading coefficient of polynomials.
• Add and subtract polynomials.
• Multiply polynomials.
• Use FOIL to multiply binomials.
• Perform operations with polynomials of several variables.

Earl is building a doghouse, whose front is in the shape of a square topped with a triangle. There will be a rectangular door through which the dog can enter and exit the house. Earl wants to find the area of the front of the doghouse so that he can purchase the correct amount of paint. Using the measurements of the front of the house, shown in Figure , we can create an expression that combines several variable terms, allowing us to solve this problem and others like it.

Figure

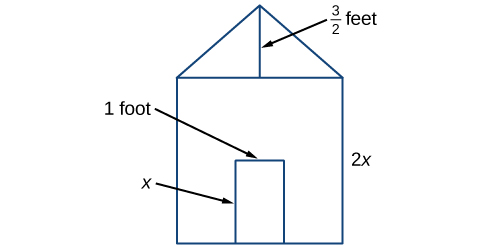
• First find the area of the square in square feet.

• Then find the area of the triangle in square feet.

• Next find the area of the rectangular door in square feet.

The area of the front of the doghouse can be found by adding the areas of the square and the triangle, and then subtracting the area of the rectangle. When we do this, we get

or

In this section, we will examine expressions such as this one, which combine several variable terms.

Identifying the Degree and Leading Coefficient of Polynomials

The formula just found is an example of a polynomial, which is a sum of or difference of terms, each consisting of a variable raised to a nonnegative integer power. A number multiplied by a variable raised to an exponent, such as , is known as a coefficient. Coefficients can be positive, negative, or zero, and can be whole numbers, decimals, or fractions. Each product , such as , is a term of a polynomial. If a term does not contain a variable, it is called a constant.

A polynomial containing only one term, such as , is called a monomial. A polynomial containing two terms, such as , is called a binomial. A polynomial containing three terms, such as , is called a trinomial.

We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form.

Polynomials

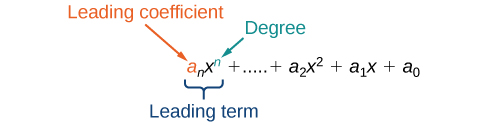
A polynomial is an expression that can be written in the form

Each real number ai is called a coefficient. The number that is not multiplied by a variable is called aconstant. Each product is a term of a polynomial. The highest power of the variable that occurs in the polynomial is called the degree of a polynomial. The leading term is the term with the highest power, and its coefficient is called the leading coefficient.

How to: Given a polynomial expression, identify the degree and leading coefficient.

1. Find the highest power of x to determine the degree.
2. Identify the term containing the highest power of x to find the leading term.
3. Identify the coefficient of the leading term.

Example : Identifying the Degree and Leading Coefficient of a Polynomial

For the following polynomials, identify the degree, the leading term, and the leading coefficient.

Solution

1. The highest power of is , so the degree is . The leading term is the term containing that degree, . The leading coefficient is the coefficient of that term, .
2. The highest power of is , so the degree is . The leading term is the term containing that degree, . The leading coefficient is the coefficient of that term, .
3. The highest power of is , so the degree is . The leading term is the term containing that degree, , The leading coefficient is the coefficient of that term, −1.

Exercise

Identify the degree, leading term, and leading coefficient of the polynomial .

Answer

The degree is , the leading term is , and the leading coefficient is .

Adding and Subtracting Polynomials

We can add and subtract polynomials by combining like terms, which are terms that contain the same variables raised to the same exponents. For example, and are like terms, and can be added to get , but and are not like terms, and therefore cannot be added.

How to: Given multiple polynomials, add or subtract them to simplify the expressions.

1. Combine like terms.
2. Simplify and write in standard form.

Example : Adding Polynomials

Find the sum.

Solution

$$\begin{align*} &4x^3+(12x^2+8x^2)+(9x-5x)+(-21+20)\qquad \text{Combine like terms} \\ &4x^3+20x^2+4x-1\qquad \qquad \qquad \qquad \qquad \qquad \; \; \; \text{Simplify} \end{align*}$$

Analysis

We can check our answers to these types of problems using a graphing calculator. To check, graph the problem as given along with the simplified answer. The two graphs should be equivalent. Be sure to use the same window to compare the graphs. Using different windows can make the expressions seem equivalent when they are not.

Exercise $\PageIndex{2}$

Find the sum.

$(2x^3+5x^2−x+1)+(2x^2−3x−4)$

Answer

$2x^3+7x^2−4x−3$

Example $\PageIndex{3}$: Subtracting Polynomials

Find the difference.

$(7x^4−x^2+6x+1)−(5x^3−2x^2+3x+2)$

Solution

$7x^4−5x^3+(−x^2+2x^2)+(6x−3x)+(1−2)$ Combine like terms

$7x^4−5x^3+x^2+3x−1$ Simplify

Analysis

Note that finding the difference between two polynomials is the same as adding the opposite of the second polynomial to the first.

Exercise $\PageIndex{3}$

Find the difference.

$(−7x^3−7x^2+6x−2)−(4x^3−6x^2−x+7)$

Answer

$−11x^3−x^2+7x−9$

Multiplying Polynomials

Multiplying polynomials is a bit more challenging than adding and subtracting polynomials. We must use the distributive property to multiply each term in the first polynomial by each term in the second polynomial. We then combine like terms. We can also use a shortcut called the FOIL method when multiplying binomials. Certain special products follow patterns that we can memorize and use instead of multiplying the polynomials by hand each time. We will look at a variety of ways to multiply polynomials.

Multiplying Polynomials Using the Distributive Property

To multiply a number by a polynomial, we use the distributive property. The number must be distributed to each term of the polynomial. We can distribute the $2$ in $2(x+7)$ to obtain the equivalent expression $2x+14$. When multiplying polynomials, the distributive property allows us to multiply each term of the first polynomial by each term of the second. We then add the products together and combine like terms to simplify.

How to: Given the multiplication of two polynomials, use the distributive property to simplify the expression.

1. Multiply each term of the first polynomial by each term of the second.
2. Combine like terms.
3. Simplify.

Example $\PageIndex{4}$: Multiplying Polynomials Using the Distributive Property

Find the product.

$(2x+1)(3x^2−x+4)$

Solution

$$\begin{align*} &2x(3x^2-x+4)+1(3x^2-x+4)\qquad \text{ Use the distributive property }\\ &(6x^3-2x^2+8x)+(3x^2-x+4)\qquad \text{ Multiply }\\ &6x^3+(-2x^2+3x^2)+(8x-x)+4\qquad \text{ Combine like terms } \\ &6x^3+x^2+7x+4\qquad \text{ Simplify } \end{align*}$$

Analysis

We can use a table to keep track of our work, as shown in Table $\PageIndex{1}$. Write one polynomial across the top and the other down the side. For each box in the table, multiply the term for that row by the term for that column. Then add all of the terms together, combine like terms, and simplify.

Table $\PageIndex{1}$

	$3x^2$	$−x$	$+4$
$2x$	$6x^3$	$−2x^2$	$8x$
$+1$	$3x^2$	$−x$	$4$

Exercise $\PageIndex{4}$

Find the product.

$(3x+2)(x^3−4x^2+7)$

Answer

$3x^4−10x^3−8x^2+21x+14$

Using FOIL to Multiply Binomials

A shortcut called FOIL is sometimes used to find the product of two binomials. It is called FOIL because we multiply the first terms, the outer terms, the inner terms, and then the last terms of each binomial.

The FOIL method arises out of the distributive property. We are simply multiplying each term of the first binomial by each term of the second binomial, and then combining like terms.

FOIL to simplify expression

Given two binomials, use FOIL to simplify the expression.

1. Multiply the outer terms of the binomials.
2. Multiply the last terms of each binomial.
3. Combine like terms and simplify.

Example $\PageIndex{5}$: Using FOIL to Multiply Binomials

Use FOIL to find the product.

$(2x−10)(3x+3) \nonumber$

Solution

Find the product of the first terms.

Find the product of the outer terms.

Find the product of the inner terms.

Find the product of the last terms.

$$\begin{align*} &6x^2+6x-54x-54\qquad \text{Add the products}\\ &6x^2+(6x-54x)-54\qquad \text{Combine like terms} \\ &6x^2-48x-54\qquad \qquad \qquad \text{Simplify} \end{align*}$$

Exercise $\PageIndex{5}$

Use FOIL to find the product.

$(x+7)(3x−5)$

Answer

$3x^2+16x−35$

Perfect Square Trinomials

Certain binomial products have special forms. When a binomial is squared, the result is called a perfect square trinomial. We can find the square by multiplying the binomial by itself. However, there is a special form that each of these perfect square trinomials takes, and memorizing the form makes squaring binomials much easier and faster. Let’s look at a few perfect square trinomials to familiarize ourselves with the form.

${(x+5)}^2=x^2+10x+25$

${(x-3)}^2=x^2-6x+9$

${(4x-1)}^2=16x^2-8x+1$

Notice that the first term of each trinomial is the square of the first term of the binomial and, similarly, the last term of each trinomial is the square of the last term of the binomial. The middle term is double the product of the two terms. Lastly, we see that the first sign of the trinomial is the same as the sign of the binomial.

Perfect Square Trinomials

When a binomial is squared, the result is the first term squared added to double the product of both terms and the last term squared.

$${(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2$$

How to: Given a binomial, square it using the formula for perfect square trinomials.

1. Square the first term of the binomial.
2. Square the last term of the binomial.
3. For the middle term of the trinomial, double the product of the two terms.
4. Add and simplify.

Example $\PageIndex{6}$: Expanding Perfect Squares

Expand $(3x−8)^2$.

Solution

Begin by squaring the first term and the last term. For the middle term of the trinomial, double the product of the two terms.

$$\begin{align*} &{(3x)}^2-2(3x)(8)+{(-8)}^2 \\ &9x^2-48x+64\qquad \qquad \; \; \; \; \text{Simplify} \end{align*}$$

Exercise $\PageIndex{6}$

Expand ${(4x−1)}^2$.

Answer

$16x^2−8x+1$

Difference of Squares

Another special product is called the difference of squares, which occurs when we multiply a binomial by another binomial with the same terms but the opposite sign. Let’s see what happens when we multiply $(x+1)(x−1)$ using the FOIL method.

$$\begin{align*} (x+1)(x-1) &= x^2-x+x-1\\ &= x^2-1 \end{align*}$$

The middle term drops out, resulting in a difference of squares. Just as we did with the perfect squares, let’s look at a few examples.

$(x+5)(x-5)=x^2-25$

$(x+11)(x-11)=x^2-121$

$(2x+3)(2x-3)=4x^2-9$

Because the sign changes in the second binomial, the outer and inner terms cancel each other out, and we are left only with the square of the first term minus the square of the last term.

Q&A

Is there a special form for the sum of squares?

No. The difference of squares occurs because the opposite signs of the binomials cause the middle terms to disappear. There are no two binomials that multiply to equal a sum of squares.

Difference of Squares

When a binomial is multiplied by a binomial with the same terms separated by the opposite sign, the result is the square of the first term minus the square of the last term.

$$(a+b)(a−b)=a^2−b^2$$

Howto: Given a binomial multiplied by a binomial with the same terms but the opposite sign, find the difference of squares.

1. Square the first term of the binomials.
2. Square the last term of the binomials.
3. Subtract the square of the last term from the square of the first term.

Example $\PageIndex{7}$: Multiplying Binomials Resulting in a Difference of Squares

Multiply $(9x+4)(9x−4)$.

Solution

Square the first term to get ${(9x)}^2=81x^2$. Square the last term to get $4^2=16$. Subtract the square of the last term from the square of the first term to find the product of $81x^2−16$.

Exercise $\PageIndex{7}$

Multiply $(2x+7)(2x−7)$.

Answer

$4x^2−49$

Performing Operations with Polynomials of Several Variables

We have looked at polynomials containing only one variable. However, a polynomial can contain several variables. All of the same rules apply when working with polynomials containing several variables. Consider an example:

$$\begin{align*} &(a+2b)(4a-b-c) a(4a-b-c)+2b(4a-b-c)\qquad \text{ Use the distributive property }\\ &4a^2-ab-ac+8ab-2b^2-2bc\qquad \qquad\qquad\qquad\qquad \text{ Multiply }\\ &4a^2+(-ab+8ab)-ac-2b^2-2bc\qquad \qquad\qquad\qquad \; \text{ Combine like terms } \\ &4a^2+7ab-ac-2bc-2b^2\qquad \qquad \qquad \qquad \qquad \qquad\text{ Simplify } \end{align*}$$

Example $\PageIndex{8}$: Multiplying Polynomials Containing Several Variables

Multiply $(x+4)(3x−2y+5)$.

Solution

$$\begin{align*} &x(3x-2y+5)+4(3x-2y+5)\qquad \text{ Use the distributive property }\\ &3x^2-2xy+5x+12x-8y+20\qquad \text{ Multiply }\\ &3x^2-2xy+(5x+12x)-8y+20\qquad \text{ Combine like terms } \\ &3x^2-2xy+17x-8y+20\qquad \qquad\text{ Simplify } \end{align*}$$

Exercise $\PageIndex{8}$

Multiply $(3x−1)(2x+7y−9)$.

Answer

$6x^2+21xy−29x−7y+9$

Media

Access these online resources for additional instruction and practice with polynomials.

1. Adding and Subtracting Polynomials
2. Multiplying Polynomials
3. Special Products of Polynomials

Key Equations

perfect square trinomial	${(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2$
difference of squares	$(a+b)(a−b)=a^2−b^2$

Key Concepts

• A polynomial is a sum of terms each consisting of a variable raised to a non-negative integer power. The degree is the highest power of the variable that occurs in the polynomial. The leading term is the term containing the highest degree, and the leading coefficient is the coefficient of that term. See Example.
• We can add and subtract polynomials by combining like terms. See Example and Example.
• To multiply polynomials, use the distributive property to multiply each term in the first polynomial by each term in the second. Then add the products. See Example.
• FOIL (First, Outer, Inner, Last) is a shortcut that can be used to multiply binomials. See Example.
• Perfect square trinomials and difference of squares are special products. See Example and Example.
• Follow the same rules to work with polynomials containing several variables. See Example.

 

Homework Exercises 1.4

WeBWorK problems:

Login with LibreOne to view this question

NOTE: If you typically access ADAPT assignments through an LMS like Canvas, you should open this page there.

Login

Login with LibreOne to view this question

NOTE: If you typically access ADAPT assignments through an LMS like Canvas, you should open this page there.

Login

Written problems: 

Write the given polynomials in standard form.

1. $1 − x − x^{2}$
2. $y − 5 + y^{2}$
3. $y − 3y^{2} + 5 − y^{3}$
4. $8 − 12a^{2} + a^{3} − a$
5. $2 − x^{2} + 6x − 5x^{3} + x^{4}$
6. $a^{3} − 5 + a^{2} + 2a^{4} − a^{5} + 6a$

Answer

1. $- x ^ { 2 } - x + 1$

3. $- y ^ { 3 } - 3 y ^ { 2 } + y + 5$

5. $x ^ { 4 } - 5 x ^ { 3 } - x ^ { 2 } + 6 x + 2$

Classify the given polynomial as a monomial, binomial, or trinomial and state the degree.

7. $x^{2} − x + 2$

8. $5 − 10x^{3}$

9. $x^{2}y^{2} + 5xy − 6$

10. $−2x^{3}y^{2}$

11. $x^{4} − 1$

12. $5$

Answer

7. Trinomial; degree $2$

9. Trinomial; degree $4$

11. Binomial; degree $4$

State whether the polynomial is linear or quadratic and give the leading coefficient.

13. $1 − 9x^{2}$

14. $10x^{2}$

15. $2x − 3$

16. $100x$

17. $5x^{2} + 3x − 1$

18. $x − 1$

19. $x − 6 − 2x^{2}$

20. $1 − 5x$

Answer

13. Quadratic, $−9$

15. Linear, $2$

17. Quadratic, $5$

19. Quadratic, $−2$

Add or Subtract as indicated

21. $\left( 5 x ^ { 2 } - 3 x - 2 \right) + \left( 2 x ^ { 2 } - 6 x + 7 \right)$

22. $\left( x ^ { 2 } + 7 x - 12 \right) + \left( 2 x ^ { 2 } - x + 3 \right)$

23. $\left( x ^ { 2 } + 5 x + 10 \right) + \left( x ^ { 2 } - 10 \right)$

24. $\left( x ^ { 2 } - 1 \right) + ( 4 x + 2 )$

25. $\left( 10 x ^ { 2 } + 3 x - 2 \right) - \left( x ^ { 2 } - 6 x + 1 \right)$

26. $\left( x ^ { 2 } - 3 x - 8 \right) - \left( 2 x ^ { 2 } - 3 x - 8 \right)$

27. $\left( \frac { 2 } { 3 } x ^ { 2 } + \frac { 3 } { 4 } x - 1 \right) - \left( \frac { 1 } { 6 } x ^ { 2 } + \frac { 5 } { 2 } x - \frac { 1 } { 2 } \right)$

28. $\left( \frac { 4 } { 5 } x ^ { 2 } - \frac { 5 } { 8 } x + \frac { 10 } { 6 } \right) - \left( \frac { 3 } { 10 } x ^ { 2 } - \frac { 2 } { 3 } x + \frac { 3 } { 5 } \right)$

29. $\left( x ^ { 2 } y ^ { 2 } + 7 x y - 5 \right) - \left( 2 x ^ { 2 } y ^ { 2 } + 5 x y - 4 \right)$

30. $\left( x ^ { 2 } - y ^ { 2 } \right) - \left( x ^ { 2 } + 6 x y + y ^ { 2 } \right)$

31. $\left( a ^ { 2 } b ^ { 2 } + 5 a b - 2 \right) + ( 7 a b - 2 ) - \left( 4 - a ^ { 2 } b ^ { 2 } \right)$

32. $\left( a ^ { 2 } + 9 a b - 6 b ^ { 2 } \right) - \left( a ^ { 2 } - b ^ { 2 } \right) + 7 a b$

33. $\left( 10 x ^ { 2 } y - 8 x y + 5 x y ^ { 2 } \right) - \left( x ^ { 2 } y - 4 x y \right) + \left( x y ^ { 2 } + 4 x y \right)$

34. $\left( 2 m ^ { 2 } n - 6 m n + 9 m n ^ { 2 } \right) - \left( m ^ { 2 } n + 10 m n \right) - m ^ { 2 } n$

35. $\left( 8 x ^ { 2 } y ^ { 2 } - 5 x y + 2 \right) - \left( x ^ { 2 } y ^ { 2 } + 5 \right) + ( 2 x y - 3 )$

36. $\left( x ^ { 2 } - y ^ { 2 } \right) - \left( 5 x ^ { 2 } - 2 x y - y ^ { 2 } \right) - \left( x ^ { 2 } - 7 x y \right)$

37. $\left( \frac { 1 } { 6 } a ^ { 2 } - 2 a b + \frac { 3 } { 4 } b ^ { 2 } \right) - \left( \frac { 5 } { 3 } a ^ { 2 } + \frac { 4 } { 5 } b ^ { 2 } \right) + \frac { 11 } { 8 } a b$

38. $\left( \frac { 5 } { 2 } x ^ { 2 } - 2 y ^ { 2 } \right) - \left( \frac { 7 } { 5 } x ^ { 2 } - \frac { 1 } { 2 } x y + \frac { 7 } { 3 } y ^ { 2 } \right) - \frac { 1 } { 2 } x y$

39. $\left( x ^ { 2 n } + 5 x ^ { n } - 2 \right) + \left( 2 x ^ { 2 n } - 3 x ^ { n } - 1 \right)$

40. $\left( 7 x ^ { 2 n } - x ^ { n } + 5 \right) - \left( 6 x ^ { 2 n } - x ^ { n } - 8 \right)$

41. Subtract $4y − 3$ from $y^{2} + 7y − 10$.

42. Subtract $x^{2} + 3x − 2$ from $2x^{2} + 4x − 1$.

43. A right circular cylinder has a height that is equal to the radius of the base, $h = r$. Find a formula for the surface area in terms of $h$.

44. A rectangular solid has a width that is twice the height and a length that is $3$ times that of the height. Find a formula for the surface area in terms of the height.

Answers

21. $7 x ^ { 2 } - 9 x + 5$

23. $2 x ^ { 2 } + 5 x$

25. $9 x ^ { 2 } + 9 x - 3$

27. $\frac { 1 } { 2 } x ^ { 2 } - \frac { 7 } { 4 } x - \frac { 1 } { 2 }$

29. $- x ^ { 2 } y ^ { 2 } + 2 x y - 1$

31. $2 a ^ { 2 } b ^ { 2 } + 12 a b - 8$

33. $9 x ^ { 2 } y + 6 x y ^ { 2 }$

35. $7 x ^ { 2 } y ^ { 2 } - 3 x y - 6$

37. $- \frac { 3 } { 2 } a ^ { 2 } - \frac { 5 } { 8 } a b - \frac { 1 } { 20 } b ^ { 2 }$

39. $- \frac { 3 } { 2 } a ^ { 2 } - \frac { 5 } { 8 } a b - \frac { 1 } { 20 } b ^ { 2 }$

41. $y ^ { 2 } + 3 y - 7$

43. $S A = 4 \pi h ^ { 2 }$

Multiply

45. $- 8 x ^ { 2 } \cdot 2 x$

46. $- 10 x ^ { 2 } y \cdot 5 x ^ { 3 } y ^ { 2 }$

47. $2 x ( 5 x - 1 )$

48. $- 4 x ( 3 x - 5 )$

49. $7 x ^ { 2 } ( 2 x - 6 )$

50. $- 3 x ^ { 2 } \left( x ^ { 2 } - x + 3 \right)$

51. $- 5 y ^ { 4 } \left( y ^ { 2 } - 2 y + 3 \right)$

52. $\frac { 5 } { 2 } a ^ { 3 } \left( 24 a ^ { 2 } - 6 a + 4 \right)$

53. $2 x y \left( x ^ { 2 } - 7 x y + y ^ { 2 } \right)$

54. $- 2 a ^ { 2 } b \left( a ^ { 2 } - 3 a b + 5 b ^ { 2 } \right)$

55. $x ^ { n } \left( x ^ { 2 } + x + 1 \right)$

56. $x ^ { n } \left( x ^ { 2 n } - x ^ { n } - 1 \right)$

57. $( x + 4 ) ( x - 5 )$

58. $( x - 7 ) ( x - 6 )$

59. $( 2 x - 3 ) ( 3 x - 1 )$

60. $( 9 x + 1 ) ( 3 x + 2 )$

61. $\left( 3 x ^ { 2 } - y ^ { 2 } \right) \left( x ^ { 2 } - 5 y ^ { 2 } \right)$

62. $\left( 5 y ^ { 2 } - x ^ { 2 } \right) \left( 2 y ^ { 2 } - 3 x ^ { 2 } \right)$

63. $( 3 x + 5 ) ( 3 x - 5 )$

64. $( x + 6 ) ( x - 6 )$

65. $\left( a ^ { 2 } - b ^ { 2 } \right) \left( a ^ { 2 } + b ^ { 2 } \right)$

66. $( a b + 7 ) ( a b - 7 )$

67. $\left( 4 x - 5 y ^ { 2 } \right) \left( 3 x ^ { 2 } - y \right)$

68. $( x y + 5 ) ( x - y )$

69. $( x - 5 ) \left( x ^ { 2 } - 3 x + 8 \right)$

70. $( 2 x - 7 ) \left( 3 x ^ { 2 } - x + 1 \right)$

71. $\left( x ^ { 2 } + 7 x - 1 \right) \left( 2 x ^ { 2 } - 3 x - 1 \right)$

72. $\left( 4 x ^ { 2 } - x + 6 \right) \left( 5 x ^ { 2 } - 4 x - 3 \right)$

73. $( x + 8 ) ^ { 2 }$

74. $( x - 3 ) ^ { 2 }$

75. $( 2 x - 5 ) ^ { 2 }$

76. $( 3 x + 1 ) ^ { 2 }$

77. $( a - 3 b ) ^ { 2 }$

78. $( 7 a - b ) ^ { 2 }$

79. $\left( x ^ { 2 } + 2 y ^ { 2 } \right) ^ { 2 }$

80. $\left( x ^ { 2 } - 6 y \right) ^ { 2 }$

81. $\left( a ^ { 2 } - a + 5 \right) ^ { 2 }$

82. $\left( x ^ { 2 } - 3 x - 1 \right) ^ { 2 }$

83. $( x - 3 ) ^ { 3 }$

84. $( x + 2 ) ^ { 3 }$

85. $( 3x + 1 ) ^ { 3 }$

86. $( 2x - 3 ) ^ { 3 }$

87. $( x + 2 ) ^ { 4 }$

88. $( x - 3 ) ^ { 4 }$

89. $( 2x - 1 ) ^ { 4 }$

90. $( 3x - 1 ) ^ { 4 }$

91. $\left( x ^ { 2 n } + 5 \right) \left( x ^ { 2 n } - 5 \right)$

92. $\left( x ^ { n } - 1 \right) \left( x ^ { 2 n } + 4 x ^ { n } - 3 \right)$

93. $\left( x ^ { 2 n } - 1 \right) ^ { 2 }$

94. $\left( x ^ { 3 n } + 1 \right) ^ { 2 }$

95. Find the product of $3x-2$ and $x^{2}-5x-2$.

96. Find the product of $x^{2}+4$ and $x^{3}-1$.

97. Each side of a square measures $3x^{3}$ units. Determine the area in terms of $x$.

98. Each edge of a cube measures $2x^{2}$ units. Determine the volume in terms of $x$.

Answer

45. $-16x^{3}$

47. $10 x ^ { 2 } - 2 x$

49. $14 x ^ { 3 } - 42 x ^ { 2 }$

51. $- 5 y ^ { 6 } + 10 y ^ { 5 } - 15 y ^ { 4 }$

53. $2 x ^ { 3 } y - 14 x ^ { 2 } y ^ { 2 } + 2 x y ^ { 3 }$

55. $x ^ { n + 2 } + x ^ { n + 1 } + x ^ { n }$

57. $x ^ { 2 } - x - 20$

59. $6 x ^ { 2 } - 11 x + 3$

61. $3 x ^ { 4 } - 16 x ^ { 2 } y ^ { 2 } + 5 y ^ { 4 }$

63. $9 x ^ { 2 } - 25$

65. $a ^ { 4 } - b ^ { 4 }$

67. $12 x ^ { 3 } - 15 x ^ { 2 } y ^ { 2 } - 4 x y + 5 y ^ { 3 }$

69. $x ^ { 3 } - 8 x ^ { 2 } + 23 x - 40$

71. $2 x ^ { 4 } + 11 x ^ { 3 } - 24 x ^ { 2 } - 4 x + 1$

73. $x ^ { 2 } + 16 x + 64$

75. $4 x ^ { 2 } - 20 x + 25$

77. $a ^ { 2 } - 6 a b + 9 b ^ { 2 }$

79. $x ^ { 4 } + 4 x ^ { 2 } y ^ { 2 } + 4 y ^ { 4 }$

81. $a ^ { 4 } - 2 a ^ { 3 } + 11 a - 10 a + 25$

83. $x ^ { 3 } - 9 x ^ { 2 } + 27 x - 27$

85. $27 x ^ { 3 } + 27 x ^ { 2 } + 9 x + 1$

87. $x ^ { 4 } + 8 x ^ { 3 } + 24 x ^ { 2 } + 32 x + 16$

89. $16 x ^ { 4 } - 32 x ^ { 3 } + 24 x ^ { 2 } - 8 x + 1$

91. $x ^ { 4 n } - 25$

93. $x ^ { 4 n } - 2 x ^ { 2 n } + 1$

95. $3 x ^ { 3 } - 17 x ^ { 2 } + 4 x + 4$

97. $9 x ^ { 6 }$ square units