3.5: Parallel and Perpendicular Lines

Last updated
Save as PDF

Page ID: 109445

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Graph a line parallel to a given line
Graph a line perpendicular to a given line
Find the equation of a line parallel to a given line
Find the equation of a line perpendicular to a given line

Warm Up $\PageIndex{1}$

Find the reciprocal of $4, -2,$ and $1/3$
Find the equation of a line with slope $m = 1/4$ and containing the point $(8, -2)$

Answer

Add texts here. Do not delete this text first.

1/4, -2, 3
$y = \frac{1}{4}x$

Parallel and Perpendicular Lines

In the last section, we dug further into how equations in different forms are related to graphs. In this section, we are going to investigate this even more by comparing the effects of different slopes. We will do this by determining when two equations result in lines might be parallel or perpendicular to each other, or neither!

First, let's recall what the slope tells us intuitively: it describes the "steepness" of a line. This means that we can look at a slope for an equation and have some expectations for what the corresponding graph might look like:

Expectations

Lines with positive slope should slant uphill (as our eyes sweep from left to right).
Lines with negative slope should slant downhill (as our eyes sweep from left to right).
Because any horizontal line neither slants uphill nor downhill, we expect that it should have slope equal to zero.
Lines with a larger positive slope should rise more quickly than lines with a smaller positive slope.
If two lines have negative slope, then the line having the slope with larger absolute value should fall more quickly than the other line.

Because slope controls the “steepness” of a line, it is a simple matter to see that parallel lines must have the same slope.

Property: PARALLEL LINES

Let $\boldsymbol{L}_{1}$ be a line having slope $m_{1}$. Let $\boldsymbol{L}_{2}$ be a line having slope $m_{2}$. If $\boldsymbol{L}_{1}$ and $\boldsymbol{L}_{2}$ are parallel, then

\[m_{1}=m_{2}\]

That is, any two parallel lines have the same slope.

Example $\PageIndex{1}$

What is the slope of any horizontal line? What is the slope of any vertical line?

Solution

One would expect that our definition would verify that the slope of any horizontal line is zero. Select, for example, the horizontal line shown in Figure 9(a). Select the points (−3, 3) and (3, 3) on this line.

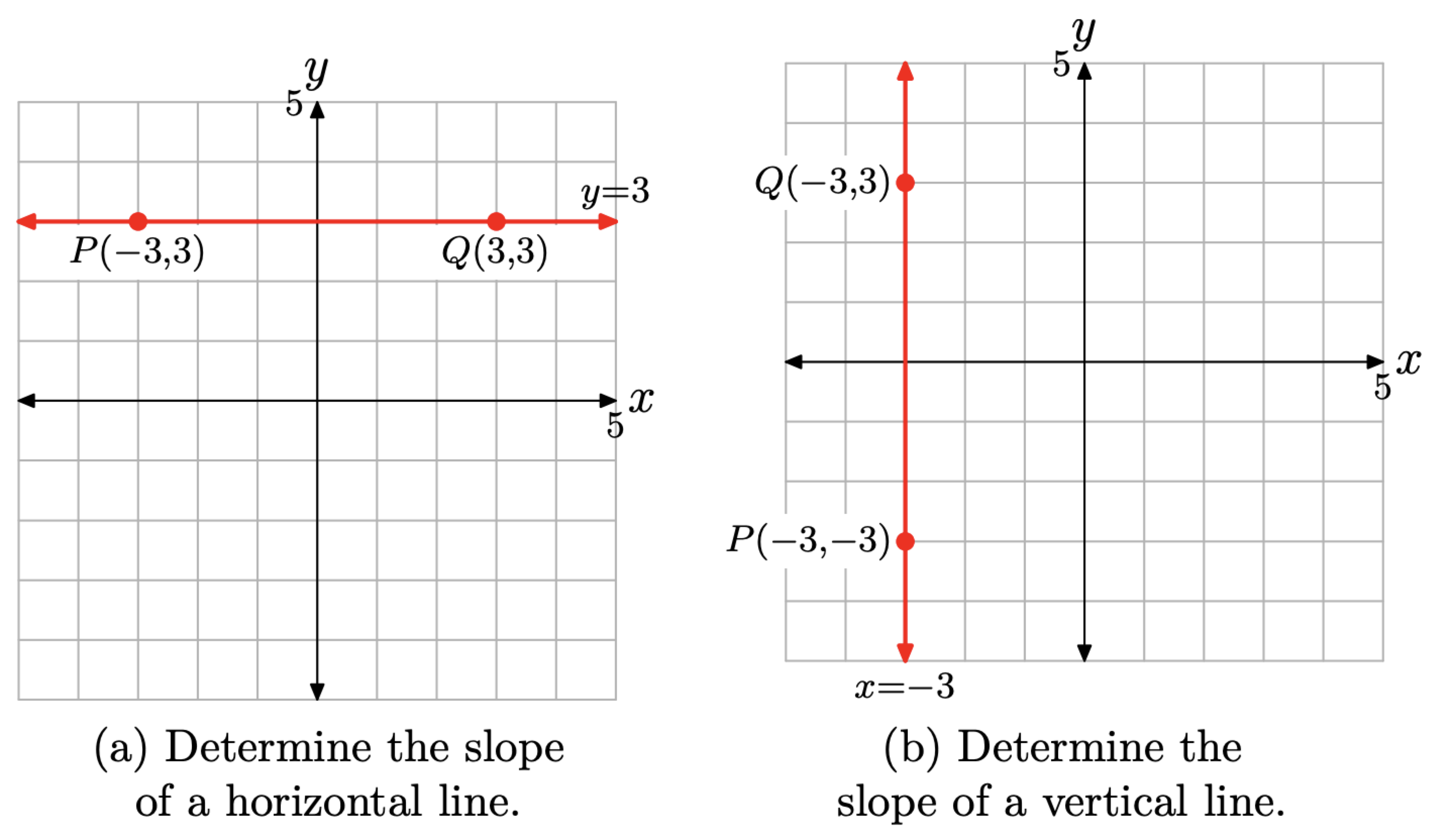
With $\left(x_{1}, y_{1}\right)=(-3,3)$ and $\left(x_{2}, y_{2}\right)=(3,3)$

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-3}{3-(-3)}=\frac{0}{6}=0\]

Thus, the horizontal line in Figure $\PageIndex{9}$(a) has slope equal to zero, exactly as expected. Further, all horizontal lines are parallel to this horizontal line and have the same slope. Therefore, all horizontal lines have slope zero.

We would surmise that the vertical line in Figure $\PageIndex{9}$(b) has undefined slope (we’ll explore this more fully in the exercises). In Figure $\PageIndex{9}$(b), we’ve selected the points P(−3, −3) and Q(−3, 3) on the vertical line. With $\left(x_{1}, y_{1}\right)=P(-3,-3)$ and $\left(x_{2}, y_{2}\right)=Q(-3,-3)$, \[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-(-3)}{-3-(-3)}=\frac{6}{0}, \text { which is undefined. }\]

The slope of the vertical line in Figure $\PageIndex{9}$(b) is undefined because division by zero is meaningless. Further, all vertical lines are parallel to this vertical line and have undefined slope.

Example $\PageIndex{2}$

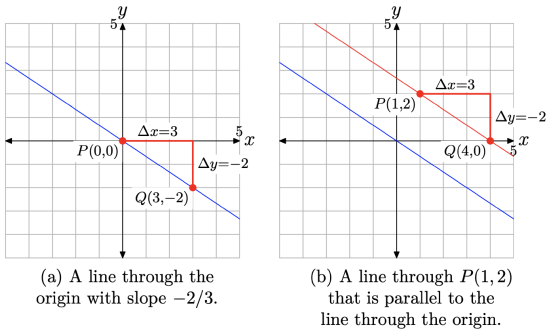
Draw a line through the point P(1, 2) that is parallel to the line passing through the origin with slope −2/3.

Solution

We will first draw a line through the origin with slope −2/3. Plot the point P(0, 0), then move 3 units to the right and 2 units downward to the point Q(3, −2), as shown in Figure $\PageIndex{10}$(a). Draw a line through the points P and Q as shown in Figure $\PageIndex{10}$(a).

Next, plot the point P(1, 2) as shown in Figure $\PageIndex{10}$(b). To draw a line through this point that is parallel to the line through the origin, this second line must have the same slope as the first line. Therefore, start at the point P(1, 2), as shown in Figure $\PageIndex{10}$(b), then move 3 units to the right and 2 units downward to the point Q(4, 0). Draw a line through the points P and Q as shown in Figure $\PageIndex{10}$(b). Note that this second line is parallel to the first.

Perpendicular Lines

The relationship between the slopes of two perpendicular lines is not as straightforward as the relation between the slopes of two parallel lines. Let’s begin by stating the pertinent property.

Property: PERPENDICULAR LINES

Let $L_{1}$ be a line having slope $m_{1}$. Let $L_{2}$ be a line having slope $m_{2}$. If $L_{1}$ and $L_{2}$ are perpendicular, then

\[m_{1} m_{2}=-1\]

That is, the product of the slopes of two perpendicular lines is −1.

We can solve equation (14) for $m_{1}$ in terms of $m_{2}$.

\[m_{1}=-\frac{1}{m_{2}}\]

Equation (15) tells us that the slope of the first line is the negative reciprocal of the slope of the second line.

For example, suppose that $L_{1}$ and $L_{2}$ are perpendicular lines with slopes $m_{1}$ and $m_{2}$, respectively

If $m_{2}=2,$ then $m_{1}=-\frac{1}{2}$
If $m_{2}=\frac{3}{5},$ then $m_{1}=-\frac{5}{3}$
If $m_{2}=-\frac{2}{3},$ then $m_{1}=\frac{3}{2}$

Note that in each bulleted item, the product of the slopes is −1.

We won’t provide a proof of equation (15), but we will provide some motivating evidence in the form of a graph.

Example $\PageIndex{3}$

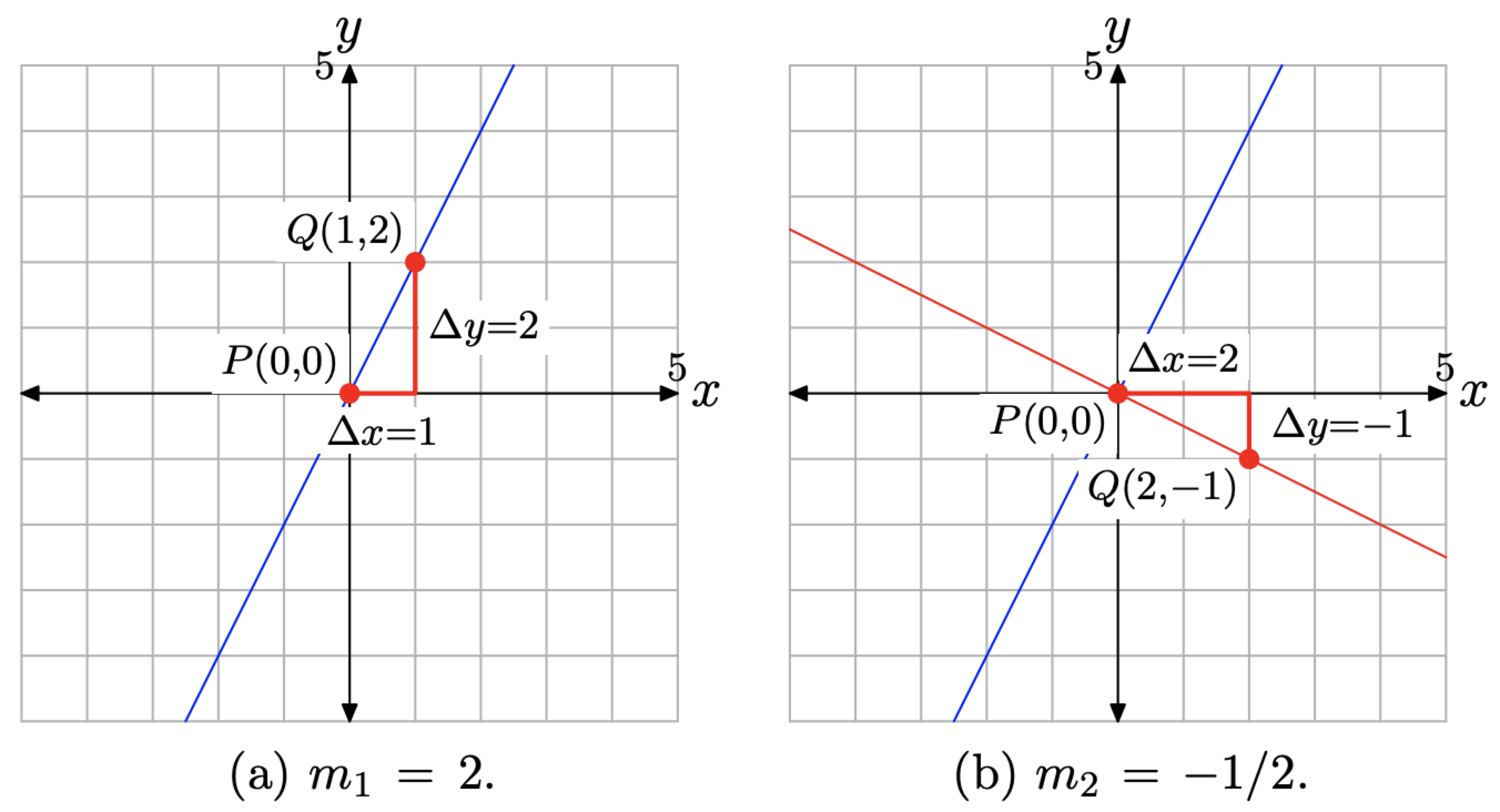
Sketch the graphs of the lines passing through the origin having slopes 2 and −1/2.

Solution

In Figure $\PageIndex{11}$(a), we’ve plotted the point P(0, 0) at the origin, then moved 1 unit to the right and 2 units upward to the point Q(1, 2). The resulting line passes through the origin and has slope $m_{1}=2$ (alternatively, $m_{1}=2 / 1$).

In Figure $\PageIndex{11}$(b), we’ve again plotted the point P(0, 0) at the origin, then moved 2 units to the right and 1 unit downward to the point Q(2, −1). The resulting line passes through the origin and has slope $m_{2}=-1 / 2$.

There are two important points that need to be made about the lines in Figure $\PageIndex{11}$(b).

The two lines in Figure $\PageIndex{11}$(b) are perpendicular. They meet and form a right angle of $90^{\circ}$. If you have a protractor available, you might want to measure the angle between the two lines and note that the measure of the angle is $90^{\circ}$.

The product of the two slopes is

\[m_{1} m_{2}=2 \cdot\left(-\frac{1}{2}\right)=-1\]

Figure $\PageIndex{11}$. Sketching perpendicular lines.

Let's summarize:

Parallel lines have the same slope $m$
Perpendicular lines have negative reciprocal slopes. That is, if a line has slope $m$, any line perpendicular to it must have slope $-1/m$.

Find an Equation of a Line Parallel to a Given Line

Since there are very specific rules about the slopes of lines that are parallel or perpendicular to each other, this makes it possible to use the equation of a line to determine the equation of another line that is parallel or perpendicular to it. Let's start with when we want to find a line parallel to another line.

Suppose we need to find an equation of a line that passes through a specific point and is parallel to a given line. We can use the fact that parallel lines have the same slope. So we will have a point and the slope—just what we need to use the point-slope equation.

First, let’s look at this graphically.

This graph shows $y=2x−3.$ We want to graph a line parallel to this line and passing through the point $(−2,1)$.

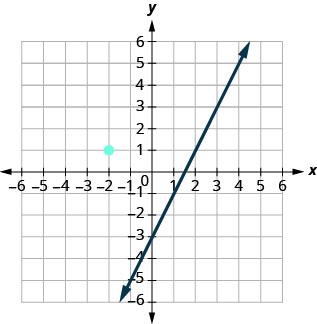
$This figure has a graph of a straight line and a point on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (0, negative 3), (1, negative 1), and (2, 1). The point (negative 2, 1) is plotted. The line does not go through the point (negative 2, 1).$

We know that parallel lines have the same slope. So the second line will have the same slope as $y=2x−3$. That slope is $m_∥=2$. We’ll use the notation m∥m∥ to represent the slope of a line parallel to a line with slope m. (Notice that the subscript || looks like two parallel lines.)

The second line will pass through $(−2,1)$ and have $m=2$.

To graph the line, we start at$(−2,1)$ and count out the rise and run.

With $m=2$ (or $m=\frac{2}{1}$), we count out the rise 2 and the run 1. We draw the line, as shown in the graph.

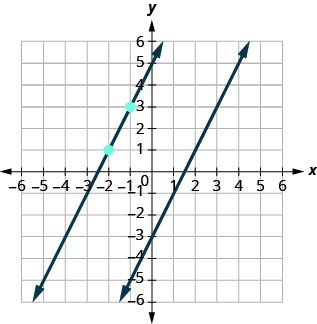
$This figure has a graph of a two straight lines on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The first line goes through the points (0, negative 3), (1, negative 1), and (2, 1). The points (negative 2, 1) and (negative 1, 3) are plotted. The second line goes through the points (negative 2, 1) and (negative 1, 3).$

Do the lines appear parallel? Does the second line pass through$(−2,1)$?

We were asked to graph the line, now let’s see how to do this algebraically.

We can use either the slope-intercept form or the point-slope form to find an equation of a line. Here we know one point and can find the slope. So we will use the point-slope form.

How to Find the Equation of a Line Parallel to a Given Line and a Point

Exercise $\PageIndex{4}$

Find an equation of a line parallel to $y=2x−3$ that contains the point $(−2,1)$. Write the equation in slope-intercept form.

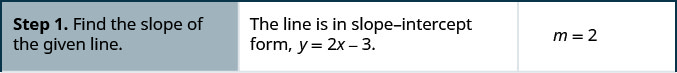
Answer: $Step 1 is to find the slope of the given line. The line is in slope-intercept form, y equals 2 x minus 3. m equals 2.$ $Step 2 is to find the slope of the parallel line. Parallel lines have the same slope. m equals 2.$ $Step 3 is to identify the point. The given point is (negative 2, 1). x 1 is negative 2 and y 1 is 1.$ $Step 4 is to substitute the values into the point-slope form y minus y 1 equals m times the quantity x minus x 1 in parentheses. y minus 1 equals 2 times the quantity x minus negative 2 in parentheses. This simplifies to y minus 1 equals 2 x plus 4.$ $Step 5 is to write the equation in slope-intercept form. y equals 2 x plus 5.$

Look at graph with the parallel lines shown previously. Does this equation make sense? What is the y-intercept of the line? What is the slope?

Exercise$\PageIndex{5}$

Find an equation of a line parallel to the line $y=3x+1$ that contains the point $(4,2)$. Write the equation in slope-intercept form.

Answer: $y=3x−10$

Exercise $\PageIndex{6}$

Find an equation of a line parallel to the line $y=12x−3$ that contains the point $(6,4)$.

Write the equation in slope-intercept form.

Answer: $y=\frac{1}{2}x+1$

FIND AN EQUATION OF A LINE PARALLEL TO A GIVEN LINE.

Find the slope of the given line.
Find the slope of the parallel line.
Identify the point.
Substitute the values into the point-slope form: $y−y_1=m(x−x_1)$.
Write the equation in slope-intercept form.

Find an Equation of a Line Perpendicular to a Given Line

Now, let’s consider perpendicular lines. Suppose we need to find a line passing through a specific point and which is perpendicular to a given line. We can use the fact that perpendicular lines have slopes that are negative reciprocals. We will again use the point-slope equation, like we did with parallel lines.

This graph shows $y=2x−3$. Now, we want to graph a line perpendicular to this line and passing through $(−2,1)$.

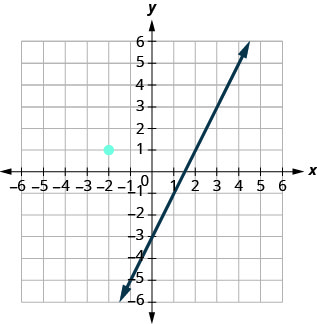
We know that perpendicular lines have slopes that are negative reciprocals.

We’ll use the notation $m_⊥$ to represent the slope of a line perpendicular to a line with slope m. (Notice that the subscript $⊥$ looks like the right angles made by two perpendicular lines.)

\[y=2x−3 perpendicular line \nonumber\]

\[m=2 m⊥=−12\nonumber\]

We now know the perpendicular line will pass through $(−2,1)$ with $m⊥=−12$.

To graph the line, we will start at $(−2,1)$ and count out the rise $−1$ and the run $2$. Then we draw the line.

$This figure has a graph of two perpendicular straight lines on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The first line goes through the points (0, negative 3), (1, negative 1), and (2, 1). The points (negative 2, 1) and (0, 0) are plotted. A right triangle is drawn connecting the points (negative 2, 1), (negative 2, 0), and (0, 0). The second line goes through the points (negative 2, 1) and (0, 0).$

Do the lines appear perpendicular? Does the second line pass through$(−2,1)$?

We were asked to graph the line, now, let’s see how to do this algebraically.

We can use either the slope-intercept form or the point-slope form to find an equation of a line. In this example we know one point, and can find the slope, so we will use the point-slope form.

How to Find the Equation of a Line Perpendicular to a Given Line and a Point

Exercise $\PageIndex{7}$

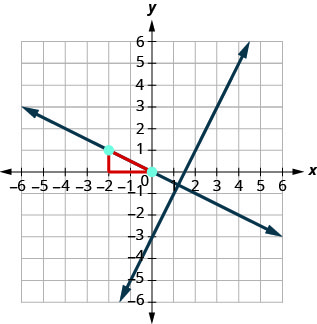
Find an equation of a line perpendicular to $y=2x−3$ that contains the point $(−2,1)$. Write the equation in slope-intercept form.

Answer: $Step 1 is to find the slope of the given line. The line is in slope-intercept form, y equals 2 x minus 3. m equals 2.$
$Step 2 is to find the slope of the perpendicular line. The slopes of perpendicular lines are negative reciprocals. m equals negative 1 divided by 2$
$Step 3 is to identify the point. The given point is (negative 2, 1). x 1 is negative 2 and y 1 is 1.$
$Step 4 is to substitute the values into the point-slope form y minus y 1 equals m times the quantity x minus x 1 in parentheses. y minus 1 equals negative 1 divided by 2 times the quantity x minus negative 2 in parentheses. This simplifies to y minus 1 equals negative 1 divided by 2 times the quantity x plus 2 in parentheses. This further simplifies to y minus 1 equals negative 1 divided by 2 times x minus 1.$
$Step 5 is to write the equation in slope-intercept form. y equals negative 1 divided by 2 times x.$

Exercise $\PageIndex{8}$

Find an equation of a line perpendicular to the line $y=3x+1$ that contains the point $(4,2)$. Write the equation in slope-intercept form.

Answer: $y=−\frac{1}{3}x+\frac{10}{3}$

Exercise $\PageIndex{9}$

Find an equation of a line perpendicular to the line $y=12x−3$ that contains the point $(6,4)$. Write the equation in slope-intercept form.

Answer: $y=−2x+16$

FIND AN EQUATION OF A LINE PERPENDICULAR TO A GIVEN LINE.

Find the slope of the given line.
Find the slope of the perpendicular line.
Identify the point.
Substitute the values into the point-slope form, $y−y_1=m(x−x_1)$.
Write the equation in slope-intercept form.

Exercise $\PageIndex{10}$

Find an equation of a line perpendicular to $x=5$ that contains the point $(3,−2)$. Write the equation in slope-intercept form.

Answer

Again, since we know one point, the point-slope option seems more promising than the slope-intercept option. We need the slope to use this form, and we know the new line will be perpendicular to x=5.x=5. This line is vertical, so its perpendicular will be horizontal. This tells us the m⊥=0.m⊥=0.

Identify the point.Identify the slope of the perpendicular line.Substitute the values intoy−y1=m(x−x1).Simplify.(3,−2)m⊥y−y1y−(−2)y+2y=====0m(x−x1)0(x−3)0−2Identify the point.(3,−2)Identify the slope of the perpendicular line.Substitute the values intoy−y1=m(x−x1).Simplify.m⊥=0y−y1=m(x−x1)y−(−2)=0(x−3)y+2=0y=−2

Sketch the graph of both lines. On your graph, do the lines appear to be perpendicular?

Exercise $\PageIndex{11}$

Find an equation of a line that is perpendicular to the line $x=4$ that contains the point $(4,−5)$. Write the equation in slope-intercept form.

Answer: $y=−5$

Exercise $\PageIndex{12}$

Find an equation of a line that is perpendicular to the line $x=2$ that contains the point $(2,−1)$. Write the equation in slope-intercept form.

Answer: $y=−1$

In Example, we used the point-slope form to find the equation. We could have looked at this in a different way.

We want to find a line that is perpendicular to $x=5$ that contains the point $(3,−2)$. This graph shows us the line $x=5$ and the point $(3,−2)$.

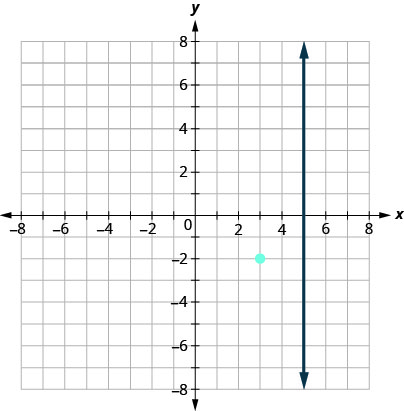
$This figure has a graph of a straight vertical line and a point on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The line goes through the points (5, 0), (5, 1), and (5, 2). The point (3, negative 2) is plotted. The line does not go through the point (3, negative 2).$

We know every line perpendicular to a vertical line is horizontal, so we will sketch the horizontal line through $(3,−2)$.

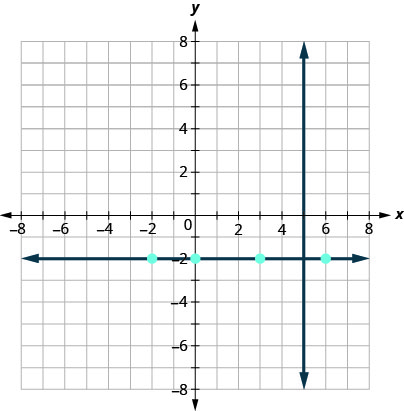
$This figure has a graph of a straight vertical line and a straight horizontal line on the x y-coordinate plane. The x and y-axes run from negative 8 to 8. The vertical line goes through the points (5, 0), (5, 1), and (5, 2). The horizontal line goes through the points (negative 2, negative 2), (0, negative 2), (3, negative 2), and (6, negative 2).$

Do the lines appear perpendicular?

If we look at a few points on this horizontal line, we notice they all have y-coordinates of $−2$. So, the equation of the line perpendicular to the vertical line $x=5$ is $y=−2$.

Exercise $\PageIndex{13}$

Find an equation of a line that is perpendicular to $y=−3$ that contains the point $(−3,5)$. Write the equation in slope-intercept form.

Answer

The line $y=−3$ is a horizontal line. Any line perpendicular to it must be vertical, in the form $x=a$. Since the perpendicular line is vertical and passes through $(−3,5)$, every point on it has an x-coordinate of $−3$. The equation of the perpendicular line is $x=−3$.

You may want to sketch the lines. Do they appear perpendicular?

Exercise $\PageIndex{14}$

Find an equation of a line that is perpendicular to the line $y=1$ that contains the point $(−5,1)$. Write the equation in slope-intercept form.

Answer: $x=−5$

Exercise $\PageIndex{15}$

Find an equation of a line that is perpendicular to the line $y=−5$ that contains the point $(−4,−5)$. Write the equation in slope-intercept form.

Answer: $x=−4$

Key Concepts

Parallel lines have the same slope
Perpendicular lines have negative reciprocal slopes

How to find an equation of a line parallel to a given line
1. Find the slope of the given line.
2. Find the slope of the parallel line.
3. Identify the point.
4. Substitute the values into the point-slope form: $y−y_1=m(x−x_1)$.
5. Write the equation in slope-intercept form.

How to find an equation of a line perpendicular to a given line
1. Find the slope of the given line.
2. Find the slope of the perpendicular line.
3. Identify the point.
4. Substitute the values into the point-slope form, $y−y_1=m(x−x_1)$.
5. Write the equation in slope-intercept form.