5.1: Simplify Rational Exponents

Learning Objectives

By the end of this section, you will be able to:

• Simplify expressions with \(a^{\frac{1}{n}}\)
• Simplify expressions with \(a^{\frac{m}{n}}\)
• Use the properties of exponents to simplify expressions with rational exponents

Warm Up

Compute or simplify

1. \(3^3\)
2. \(7^6\cdot 7^{-4}\)
3. \(a^{19}\cdot a^{14}\)
4. \(\sqrt{x^2}\)
5. \(\sqrt[3]{x^3}\)

Answer

1. 27
2. \(7^2=49\)
3. \(a^{33}\)
4. \(|x|\)
5. \(x\)

A Note about \(\sqrt[n]{x^n}\)

We recall that in earlier sections that for any integer \(n\geq 2\),

when the index \(n\) is odd \(\sqrt[n]{a^{n}}=a\)

when the index \(n\) is even \(\sqrt[n]{a^{n}}=|a|\)

We notice that if \(a>0\), that is a positive real number, then \(\sqrt[n]{a^{n}}=a\) for \(n\geq 2\) no matter if n is even or odd. Since we will be dealing with some properties that may be confusing at first, we will treat all bases as positive real numbers.

Rationalizing the denominator.

No mathematician actually cares about rationalizing the denominator but it is a student learning objective for this class so... here we go.

Say we have a fraction \(\dfrac{1}{\sqrt{2}}\) and we want to make the denominator into a rational, that is we want to rationalize the denominator. We know that \(\sqrt{2}^2=2\) and multiplying by 1 doesn't change the number, so lets multiply by \(\dfrac{\sqrt{2}}{\sqrt{2}}\) since this is just a fancy way to write 1. We get \(\dfrac{1}{\sqrt{2}}\dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{2}}{\sqrt{2}^2}=\dfrac{\sqrt{2}}{2}\).

Exercise \(\PageIndex{1}\)

Rationalize the denominator.

1. \(\dfrac{1}{\sqrt{3}}\)
2. \(\dfrac{1}{\sqrt{4}}\)
3. \(\dfrac{1}{\sqrt{5}}\)
4. \(\dfrac{1}{\sqrt{x}}\)

Answer

1. \(\dfrac{\sqrt{3}}{3}\)
2. Trick question since \(\sqrt{4}=2\) so \(\dfrac{1}{\sqrt{4}}=\dfrac{1}{2}\)
3. \(\dfrac{\sqrt{5}}{5}\)
4. \(\dfrac{\sqrt{x}}{x}\)

What about if we have a sum or difference in the denominator? For example we have \(\dfrac{1}{1+\sqrt{2}}\), what do we do? Remember \((x+y)(x-y)=x^2-y^2\)? we can use this to rationalize the denominator by using what is called the conjugate.

Definition: CONJUGATE

The conjugate of \(a+\sqrt{b}\) is \(a-\sqrt{b}\)

and the conjugate of \(a+\sqrt{b}\) is \(a-\sqrt{b}\)

So by multiplying by a sneaky 1, \(\dfrac{1-\sqrt{2}}{1-\sqrt{2}}\), we can rationalize the denominator of \(\dfrac{1}{1+\sqrt{2}}\). We get

Example \(\PageIndex{2}\)

Rationalize the denominator of \(\dfrac{1}{1+\sqrt{2}}\)

Solution

Multiply top and bottom by the conjugate of the denominator	\(=\dfrac{1}{1+\sqrt{2}}\)\(\dfrac{1-\sqrt{2}}{1-\sqrt{2}}\)
Multiply	\(=\dfrac{1-\sqrt{2}}{1^2-\sqrt{2}^2}\)
Simplify	\(=\dfrac{1-\sqrt{2}}{1-2} =\dfrac{1-\sqrt{2}}{-1}\ =1+\sqrt{2}\)

Let's do some examples

Exercise \(\PageIndex{3}\)

Rationalize the denominator

1. \(\dfrac{1}{1+\sqrt{3}}\)
2. \(\dfrac{1}{5+\sqrt{4}}\)
3. \(\dfrac{1}{2-\sqrt{5}}\)
4. \(\dfrac{1}{3+\sqrt{x}}\)
5. \(\dfrac{1}{x-\sqrt{y}}\)

Answer

1. \(\dfrac{1-\sqrt{3}}{1-3}=-\dfrac{1-\sqrt{3}}{2}\)
2. \(\dfrac{1}{5+2}=\dfrac{1}{7}\)
3. \(\dfrac{2+\sqrt{5}}{4-5}=-\dfrac{1-\sqrt{3}}{1}=1-\sqrt{3}\)
4. \(\dfrac{3-\sqrt{x}}{9-x}\)
5. \(\dfrac{x+\sqrt{y}}{x^2-y}\)

Use the Properties of Exponents to Simplify Expressions with Rational Exponents

The same properties of exponents that we have already used also apply to rational exponents. We will list the Properties of Exponents here to have them for reference as we simplify expressions.

Properties of Exponents

Properties of Exponents

If \(a\) and \(b\) are real numbers and \(m\) and \(n\) are rational numbers, then

Zero Exponent Property

\(a^{0}=1, a \neq 0\)

Negative Exponent Property

\(a^{-n}=\frac{1}{a^{n}}, a \neq 0\)

Product Property

\(a^{m} \cdot a^{n}=a^{m+n}\)

Power Property

\(\left(a^{m}\right)^{n}=a^{m \cdot n}\)

Product to a Power Property

\((a b)^{m}=a^{m} b^{m}\)

Quotient Property

\(\frac{a^{m}}{a^{n}}=a^{m-n}, a \neq 0\)

Quotient to a Power Property

\(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}, b \neq 0\)

Let's talk each property.

We saw the Zero Exponent Property in chapter 1 from dividing \(a^1\) by a.

We saw the Product Property in chapter 1 but a quick example would be \(4^2\cdot 4^3=4\cdot 4\cdot 4\cdot 4\cdot 4=4^5\)

We saw the Negative Exponent Property in chapter 1 and it follows from dividing \(a^0\) by a to get \(a^{-1}\).

To see the Power Property is true, let's consider an example. Say we have \((2^2)^3\) and from the power property, this should be \(2^6\). Computationally, this is true since \((2^2)^3=4^3=64=2^6\) but let's take a look at a picture for the intuition of why this is true.

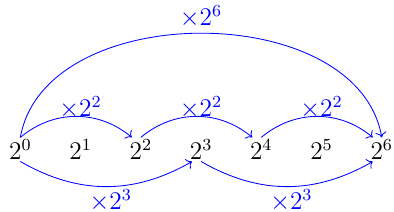
We see that it takes 3 steps of \(2^2\) to go from \(1=2^0\) to \(2^6\). This makes sense since if you take 6 normal steps then this is the same as you taking 3 double steps since \(3\cdot 2\)=6, and this is exactly what is happening in the picture above. For the same reason we see that if we take 2 triple steps then we took 6 normal steps, which is shown with the bottom arrows. So we get \((a^n)^m=a^{n\cdot m}=a^{m\cdot n}=(a^m)^n\).

The Product to a Power Property comes from noticing that multiplication is commutative, that is we can switch terms around without changing the product, i.e \(a\cdot b=b\cdot a\). So let's take a look at \((a\cdot b)^2\). Well, \((a\cdot b)^2=(a\cdot b)\cdot (a\cdot b)=a\cdot b\cdot a\cdot b=a\cdot a\cdot b\cdot b=a^2\cdot b^2\). The same thing goes for to the power of 3, \((a\cdot b)^3=a\cdot b \cdot a\cdot b \cdot a\cdot b=a\cdot a \cdot a\cdot b \cdot b\cdot b=a^3\cdot b^3\). We can apply the same reasoning to the power of 4,5, 6, all the way up to any number n.

The Quotient Property is from the product property and negative exponent property which we saw in chapter 1. That is, \(\frac{a^m}{a^n}=a^ma^{-n}=a^{m+(-n)}=a^{m-n}\)

The Quotient to a Power Property follows from the negative exponent property and product to a power property. That is, \((\frac{a}{b})^2=(ab^{-1})^2=a^2b^{-2}=\frac{a^2}{b^2}\)

Use the Properties of Exponents to Simplify Expressions with Rational Exponents

The same properties of exponents that we have already used also apply to rational exponents. We will list the Properties of Exponents here to have them for reference as we simplify expressions.

Example \(\PageIndex{4}\)

Simplify:

1. \(x^{\frac{1}{2}} \cdot x^{\frac{5}{6}}\)
2. \(\left(z^{9}\right)^{\frac{2}{3}}\)
3. \(\frac{x^{\frac{1}{3}}}{x^{\frac{5}{3}}}\)

Solution

a. The Product Property tells us that when we multiple the same base, we add the exponents.

\(x^{\frac{1}{2}} \cdot x^{\frac{5}{6}}\)

The bases are the same, so we add the exponents.

\(x^{\frac{1}{2}+\frac{5}{6}}\)

Add the fractions.

\(x^{\frac{8}{6}}\)

Simplify the exponent.

\(x^{\frac{4}{3}}\)

b. The Power Property tells us that when we raise a power to a power, we multiple the exponents.

\(\left(z^{9}\right)^{\frac{2}{3}}\)

To raise a power to a power, we multiple the exponents.

\(z^{9 \cdot \frac{2}{3}}\)

Simplify.

\(z^{6}\)

c. The Quotient Property tells us that when we divide with the same base, we subtract the exponents.

\(\frac{x^{\frac{1}{3}}}{x^{\frac{5}{3}}}\)

To divide with the same base, we subtract the exponents.

\(\frac{1}{x^{\frac{5}{3}-\frac{1}{3}}}\)

Simplify.

\(\frac{1}{x^{\frac{4}{3}}}\)

Exercise \(\PageIndex{5}\)

Simplify:

1. \(x^{\frac{1}{6}} \cdot x^{\frac{4}{3}}\)
2. \(\left(x^{6}\right)^{\frac{4}{3}}\)
3. \(\frac{x^{\frac{2}{3}}}{x^{\frac{5}{3}}}\)

Answer

1. \(x^{\frac{3}{2}}\)
2. \(x^{8}\)
3. \(\frac{1}{x}\)

Exercise \(\PageIndex{6}\)

Simplify:

1. \(y^{\frac{3}{4}} \cdot y^{\frac{5}{8}}\)
2. \(\left(m^{9}\right)^{\frac{2}{9}}\)
3. \(\frac{d^{\frac{1}{5}}}{d^{\frac{6}{5}}}\)

Answer

1. \(y^{\frac{11}{8}}\)
2. \(m^{2}\)
3. \(\frac{1}{d}\)

Sometimes we need to use more than one property. In the next example, we will use both the Product to a Power Property and then the Power Property.

Example \(\PageIndex{7}\)

Simplify:

1. \(\left(27 u^{\frac{1}{2}}\right)^{\frac{2}{3}}\)
2. \(\left(m^{\frac{2}{3}} n^{\frac{1}{2}}\right)^{\frac{3}{2}}\)

Solution:

a.

\(\left(27 u^{\frac{1}{2}}\right)^{\frac{2}{3}}\)

First we use the Product to a Power Property.

\((27)^{\frac{2}{3}}\left(u^{\frac{1}{2}}\right)^{\frac{2}{3}}\)

Rewrite \(27\) as a power of \(3\).

\(\left(3^{3}\right)^{\frac{2}{3}}\left(u^{\frac{1}{2}}\right)^{\frac{2}{3}}\)

To raise a power to a power, we multiple the exponents.

\(\left(3^{2}\right)\left(u^{\frac{1}{3}}\right)\)

Simplify.

\(9 u^{\frac{1}{3}}\)

b.

\(\left(m^{\frac{2}{3}} n^{\frac{1}{2}}\right)^{\frac{3}{2}}\)

First we use the Product to a Power Property.

\(\left(m^{\frac{2}{3}}\right)^{\frac{3}{2}}\left(n^{\frac{1}{2}}\right)^{\frac{3}{2}}\)

To raise a power to a power, we multiply the exponents.

\(m n^{\frac{3}{4}}\)

Exercise \(\PageIndex{8}\)

Simplify:

1. \(\left(32 x^{\frac{1}{3}}\right)^{\frac{3}{5}}\)
2. \(\left(x^{\frac{3}{4}} y^{\frac{1}{2}}\right)^{\frac{2}{3}}\)

Answer

1. \(8 x^{\frac{1}{5}}\)
2. \(x^{\frac{1}{2}} y^{\frac{1}{3}}\)

Exercise \(\PageIndex{9}\)

Simplify:

1. \(\left(81 n^{\frac{2}{5}}\right)^{\frac{3}{2}}\)
2. \(\left(a^{\frac{3}{2}} b^{\frac{1}{2}}\right)^{\frac{4}{3}}\)

Answer

1. \(729 n^{\frac{3}{5}}\)
2. \(a^{2} b^{\frac{2}{3}}\)

We will use both the Product Property and the Quotient Property in the next example.

Example \(\PageIndex{10}\)

Simplify:

1. \(\frac{x^{\frac{3}{4}} \cdot x^{-\frac{1}{4}}}{x^{-\frac{6}{4}}}\)
2. \(\left(\frac{16 x^{\frac{4}{3}} y^{-\frac{5}{6}}}{x^{-\frac{2}{3}} y^{\frac{1}{6}}}\right)^{\frac{1}{2}}\)

Solution:

a.

\(\frac{x^{\frac{3}{4}} \cdot x^{-\frac{1}{4}}}{x^{-\frac{6}{4}}}\)

Use the Product Property in the numerator, add the exponents.

\(\frac{x^{\frac{2}{4}}}{x^{-\frac{6}{4}}}\)

Use the Quotient Property, subtract the exponents.

\(x^{\frac{8}{4}}\)

Simplify.

\(x^{2}\)

b.

\(\left(\frac{16 x^{\frac{4}{3}} y^{-\frac{5}{6}}}{x^{-\frac{2}{3}} y^{\frac{1}{6}}}\right)^{\frac{1}{2}}\)

Use the Quotient Property, subtract the exponents.

\(\left(\frac{16 x^{\frac{6}{3}}}{y^{\frac{6}{6}}}\right)^{\frac{1}{2}}\)

Simplify.

\(\left(\frac{16 x^{2}}{y}\right)^{\frac{1}{2}}\)

Use the Product to a Power Property, multiply the exponents.

\(\frac{4 x}{y^{\frac{1}{2}}}\)

Exercise \(\PageIndex{11}\)

Simplify:

1. \(\frac{m^{\frac{2}{3}} \cdot m^{-\frac{1}{3}}}{m^{-\frac{5}{3}}}\)
2. \(\left(\frac{25 m^{\frac{1}{6}} n^{\frac{11}{6}}}{m^{\frac{2}{3}} n^{-\frac{1}{6}}}\right)^{\frac{1}{2}}\)

Answer

1. \(m^{2}\)
2. \(\frac{5 n}{m^{\frac{1}{4}}}\)

Exercise \(\PageIndex{12}\)

Simplify:

1. \(\frac{u^{\frac{4}{5}} \cdot u^{-\frac{2}{5}}}{u^{-\frac{13}{5}}}\)
2. \(\left(\frac{27 x^{\frac{4}{5}} y^{\frac{1}{6}}}{x^{\frac{1}{5}} y^{-\frac{5}{6}}}\right)^{\frac{1}{3}}\)

Answer

1. \(u^{3}\)
2. \(3 x^{\frac{1}{5}} y^{\frac{1}{3}}\)

Access these online resources for additional instruction and practice with simplifying rational exponents.

• Review-Rational Exponents
• Using Laws of Exponents on Radicals: Properties of Rational Exponents

Key Concepts

• Rational Exponent \(a^{\frac{1}{n}}\)
  • If \(\sqrt[n]{a}\) is a real number and \(n≥2\), then \(a^{\frac{1}{n}}=\sqrt[n]{a}\).
• Rational Exponent \(a^{\frac{m}{n}}\)
  • For any positive integers \(m\) and \(n\),
    \(a^{\frac{m}{n}}=(\sqrt[n]{a})^{m} \text { and } a^{\frac{m}{n}}=\sqrt[n]{a^{m}}\)
• Properties of Exponents
  • If \(a, b\) are real numbers and \(m, n\) are rational numbers, then
    • Product Property \(a^{m} \cdot a^{n}=a^{m+n}\)
    • Power Property \(\left(a^{m}\right)^{n}=a^{m \cdot n}\)
    • Product to a Power \((a b)^{m}=a^{m} b^{m}\)
    • Quotient Property \(\frac{a^{m}}{a^{n}}=a^{m-n}, a \neq 0\)
    • Zero Exponent Definition \(a^{0}=1, a \neq 0\)
    • Quotient to a Power Property \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}, b \neq 0\)
    • Negative Exponent Property \(a^{-n}=\frac{1}{a^{n}}, a \neq 0\)